作業的“精練”變式設計
——以微專題“解三角形中范圍(最值)”作業設計為例

杜海洋 李 平

(成都經濟技術開發區實驗中學校)

隨著新課改在全國范圍內的全面實施,“高效課堂”成為時代主流.為了使教學效果達到高效,課堂上的“精講”、作業的“精練”成為教學的追求目標.為了反饋課堂教學效果,檢驗的手段“課后作業”成為至關重要的一環,其中課后作業質量的高低,即作業“精練”的設計就凸顯其重要性.

變式不僅是指問題的變式,而是泛指知識形成過程中的問題設計;基本概念辨析型變式;定理、公式的深化變式,多證變式及變式應用;例題、習題的一題多解、一法多用、一題多變、多題歸一等,其中課后作業中如何設置變式“問題”才能達到最終檢測目的,即變化中的“不變性”,筆者認為作業設計的變式及思維“梯度”是變式設計的關鍵.在高中數學知識體系中,解三角形是一個基礎知識點,也是高考的一個高頻考點.在解三角形的題型中,主要考查正弦定理和余弦定理的應用,而在解三角形中涉及求面積、周長、角等最值和取值范圍是命題的熱點,也是重點、難點.筆者在高三復習時通過微專題對本專題即解三角形的范圍(最值)的方法進行優化歸納,并給出針對性鞏固練習,以期求得熱點、難點的突破.下面筆者以微專題“解三角形中范圍(最值)”作業設計為例,以饗讀者!

【作業題根設計】

作業“首題”的選擇是作業設計的核心,因為它要起到承上啟下的作用,要為本節作業內容開篇起到“引領”作用,俗話說“一個典型的事例勝過千萬句空洞的說教”,一是要回歸基本知識,二是要體現基本方法.

【題根變式設計】

變式設計一般遵循學生的最近發展,尤其是在“題根”的基礎上對其條件、結論、結構、方法等進行“變式”,筆者認為變式試題的條件和結論盡可能做到“螺旋式上升”的策略,讓學生在前面的基礎上“跳一跳,摘得到”.

【題根】(高考真題理)△ABC在內角A,B,C的對邊分別為a,b,c,已知a=bcosC+csinB.

(Ⅰ)求B;

(Ⅱ)若b=2,求△ABC面積的最大值.

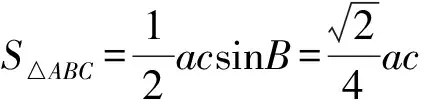
【變式1】在△ABC中,sin2A-sin2B-sin2C=sinBsinC.

(Ⅰ)求A;

(Ⅱ)若BC=3,求△ABC的周長的最大值.

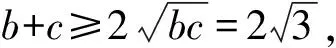
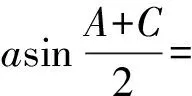
(Ⅰ)求B;

(Ⅱ)若△ABC為銳角三角形,且b=2,求△ABC周長的取值范圍.

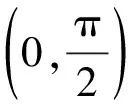
【變式3】將變式2的第(Ⅱ)問變為(Ⅱ)若△ABC為銳角三角形,且c=1,求△ABC面積的取值范圍.

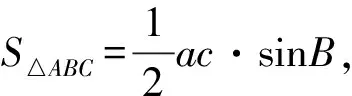
即通性通法出場,目的進一步強化解三角形的核心方法為將目標表達式轉化為角的函數.有了化角意識可讓學生利用此法去解變式1即變式1,方法2:邊化角消參化單變量.

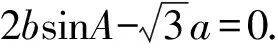
(Ⅰ)求角B的大小;

(Ⅱ)求cosA+cosB+cosC的取值范圍.

【設計意圖】(Ⅰ)問根據已知條件,利用余弦定理經過較復雜的代數恒等變形求得a2+c2-b2=ac,對運算能力要求較高;利用正弦定理邊化角,運算簡潔,是解三角形常用的方法,確定為最優解;(Ⅱ)問可運用多種方法,利用余弦定理角化邊代入化簡,運算較為麻煩,其次直接使用三角恒等變換,將化為角的三角函數進行求值,簡潔明快,確定為最優解.此訓練題設計目的是讓學生對比解法,識別題型,建立解題“模式”.

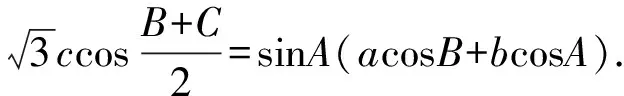
(Ⅰ)求A;

(Ⅱ)若b=1,求c的取值范圍.

【設計意圖】此題考查解三角形的綜合應用,能夠根據題干給出的信息選用合適的余弦定理公式是解題的第一個關鍵;根據三角形內角A+B+C=π的隱含條件,結合三角函數的誘導公式及正弦定理,將問題轉化為求解含∠A的表達式的最值問題是解題的第二個關鍵,注意角的限制范圍.

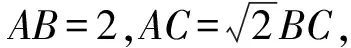
【設計意圖】在處理三角形中的邊角關系時,通法為把所求目標式轉化為關于角的函數關系,或化歸為邊的關系.題中若出現邊的一次式一般利用正弦定理,出現邊的二次式一般為“代數化”埋下伏筆,即坐標系的運用,拓展學生思維.

【答案及解析】

【題根解析】(Ⅰ)解法一:

因為a=bcosC+csinB,

所以由正弦定理得

sinA=sinBcosC+sinCsinB.①

在△ABC中,A=π-(B+C),

所以sinA=sin(B+C)=sinBcosC+sinCcosB.②

由①和②得sinBsinC=cosBsinC.

因為sinC≠0,所以sinB=cosB.

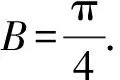
解法二:因為a=bcosC+csinB,

所以由余弦定理的推論得

即a2+c2-b2=2acsinB,

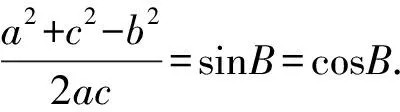
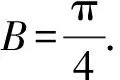
由已知及余弦定理得

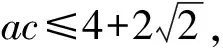
當且僅當a=c時,等號成立,

則△ABC面積的最大值為

【變式1】【解析】(Ⅰ)在△ABC中,設角A,B,C的對邊分別為a,b,c.

由正弦定理得a2-b2-c2=bc,

由余弦定得的推論得

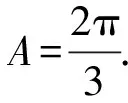
(Ⅱ)由余弦定理得

a2=b2+c2-2bccosA=b2+c2+bc=9,

即(b+c)2-bc=9.

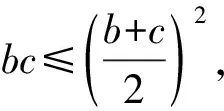
當且僅當b=c時,等號成立,

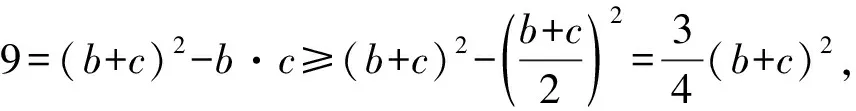
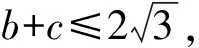
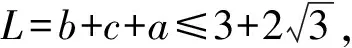
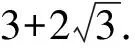
【變式2】【解析】(Ⅰ)由正弦定理得

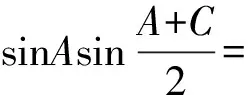
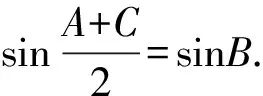
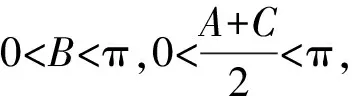
根據題意知A+B+C=π,

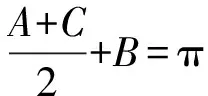
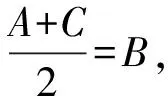
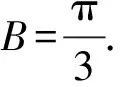
(Ⅱ)解法一:正弦定理消參化單角函數

所以△ABC的周長

L=a+b+c

因為△ABC為銳角三角形,

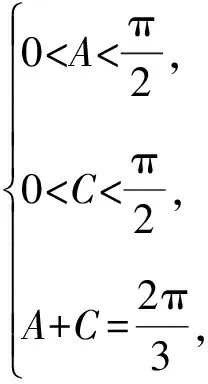
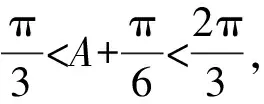
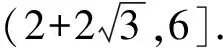
解法二:圖形分析法

易知當B為優弧AC的中點即B1處時,

△ABC的周長和面積最大,

設△ABC的周長為L,此時L=2×3=6,

當△BAC為直角三角形時,

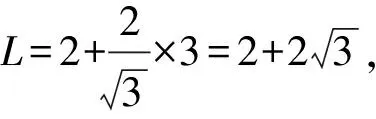
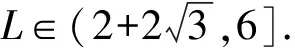
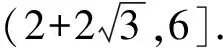
【變式3】【解析】(Ⅱ)解法一:因為△ABC是銳角三角形,

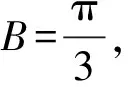
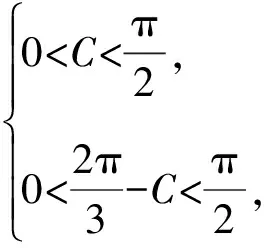
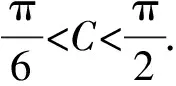
由三角形面積公式得

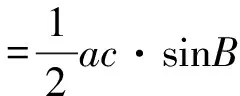
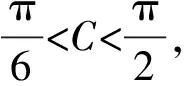
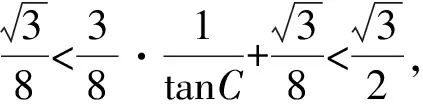
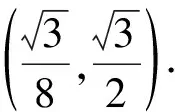
解法二:由余弦定理得b2=a2+1-a.

因為△ABC是銳角三角形,

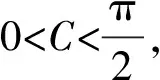
將b2=a2+1-a代入a2+b2-1>0得2a2-a>0,

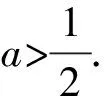
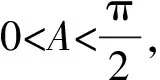
所以b2+c2-a2>0,

將b2=a2+1-a代入b2+1-a2>0得a<2,

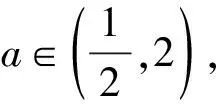
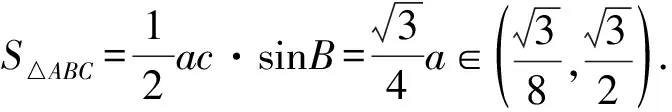
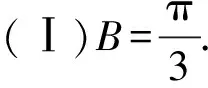
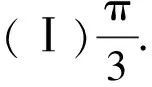
【作業變式設計】

【要點反思】

1.知識點:解三角形的相關知識,涉及到正弦定理邊角互化的應用、余弦定理及推論的應用、三角形周長、面積等最值(范圍)的求解問題.

2.解題思路運用:常規方法涉及方法1基本不等式、方法2邊化角,進而轉化為正弦函數求最值問題,其本質為轉化化歸消參策略.

3.整個作業變式設計在題型和方法上采用螺旋式上升的策略,步步設卡,而不是一下套用所謂的巧法或“秒殺”,整個過程學生思維得到鍛煉,弄清問題的來龍去脈,知識生成得到很好的訓練.

【體會】

作業是檢查學生對基礎知識、基本技能掌握程度的一種必不可少的有效手段.在作業設計中,要面向全體學生,尊重個體差異,樹立分層遞進的教學觀.在作業設計時,要根據學生的不同層次需求設計不同的練習,才能使學生在學習中達到事半功倍的效果.數學教與學的活動不僅是對原題解法上的探求,更是在原題的基礎上實現解法或認知的延伸與拓展,挖掘出更深刻的本質與結論.變式教學與作業設計則都要能凸顯概念的本質,突出問題特征,揭示知識的關聯,讓課堂教學效果更加高效.

近年的高考試題堅持“新題不難,難題不怪”的命題方向,強調“注意通性通法,淡化特殊技巧”,多數高考試題能在課本或往年高考真題中找到“原型”,不少高考題就是對課本原題或往年高考真題的變形、改造及綜合.尤其在高考復習備考中,節奏快、時間緊、容量多、內容跨度大、抽象性強,在這樣的環境下,教師更是迫切需要提高課堂效率,實現高效課堂,不是簡單地增加“刷題”量,而是需要教師對典型例題精心準備,充分挖掘,利用變式教學和課后作業精心設置的“精練”,讓學生更好地理解問題的實質,從而實現觸類旁通,舉一反三,達到事半功倍的效果.