非磁性/磁性摻雜劑對SnO2體系的性能調控

高禹 郭華忠

摘要：?本文通過第一性原理計算在GGA + ?U ?框架下系統地研究了非磁性摻雜劑（Li）和磁性摻雜劑（V）以及相應的點缺陷（V ?O /V ?Sn ）摻雜SnO ?2 基稀磁半導體（DMS）的穩定性、電子結構、鍵合性質、磁性以及光學性質. 計算得到的形成能結果表明，V元素單摻雜體系比Li元素單摻雜體系更穩定. 其中，V ?O 存在的摻雜體系穩定性更高，而V ?Sn 對摻雜體系的穩定性不利. 磁性分析表明，Li摻雜體系的磁矩大于V摻雜體系的磁矩. 當有點缺陷存在時，V ?Sn 的加入顯著提高了摻雜體系的磁性，而V ?O 對非磁性金屬元素/磁性金屬元素摻雜體系的磁性影響不同：當V ?O 存在于Li摻雜體系時，Li原子周圍的O原子自旋極化減少，因此導致磁矩降低；當V摻雜體系中有V ?O 存在，磁性不僅來源于V原子的自旋極化，同時來源于V ?O 周圍的O原子的自旋極化，因此磁矩增大. 結合電子結構分析可知，Li摻雜體系的磁性是由O-p和Li-p軌道之間的雙交換作用產生的，V摻雜體系的磁性是由O-p和V-d軌道之間的雙交換作用產生的. 鍵合分析發現V ?O 的存在可以提高兩種金屬摻雜體系鍵（Li-O和V-O）的共價性. 在可見光區域內，Sn ?1 ??5 LiO ?3 ??2 和Sn ?1 ??5 VO ?3 ??2 具有較高的光學透明度. 以上這些結果為非磁性金屬元素（Li）和磁性金屬元素（V）及相應的點缺陷（V ?O /V ?Sn ）摻雜SnO ?2 在自旋電子器件中的應用提供了新的思路.

關鍵詞：第一性原理； 摻雜劑； 點缺陷； 電子結構； 磁性； 光學性質

中圖分類號：??O47? 文獻標識碼：A? DOI：10.19907/j.0490-6756.2023.054002

收稿日期： ?2023-04-07Symbol`@@

基金項目： ?科技部重點研發計劃（2022YFF0608302）; 四川大學理科特色方向培育計劃（2020SCUNL209）

作者簡介： ??高禹（1993-）， 女， 山東威海人， 碩士研究生， 研究方向為計算凝聚態物理. E-mail： yugao@stu.scu.edu.cn

通信作者： ?郭華忠. E-mail：guohuazhong@scu.edu.cn

The optimal tuning of SnO ?2 ?systems by non-magnetic dopant/magnetic dopant

GAO Yu， GUO Hua-Zhong

（College of Physics， Sichuan University， Chengdu 610065， China）

In this paper， the stability， electronic structure， bonding stations， as well as the magnetic and optical properties of non-magnetic dopants （Li）， magnetic dopants （V）， and the corresponding point defects （V ?O /V ?Sn ） on SnO ?2 -based dilute magnetic semiconductors （DMS） are systematically investigated through ?ab-initio ?calculations. All the calculations are carried out within the GGA + ?U ?framework. The calculated formation energy results showed that the V single-doped system is more stable than the Li single-doped system. Among them， the doping system with V ?O ?had higher stability， while V ?Sn ?was unfavorable for the stability of the doping system. The magnetic analysis showed that the magnetic moment of the Li-doped system is larger than that of the V-doped system. The addition of V ?Sn ??significantly ?improved the magnetic properties of the doped system， while the presence of V ?O ?had different effects on the magnetic properties of the non-magnetic metal element/magnetic metal element doped system. When V ?O ?is present in the Li-doped system， the spin polarization of the O atoms around the Li atom is reduced， thus leading to a lower magnetic moment. When V ?O ?is set in the V-doped system， the magnetic moment increases not only from the spin polarization of the V atom but also from the spin ?polarization ?of the O atoms around V ?O . Combined with the electronic structure analysis， it is clear that a spin-polarized double exchange effect in the Li-p and O-p orbitals， which leads to magnetism of the ?Li-doped ?system， and the magnetism of the V-doped system is generated by the spin-polarized double ?exchange ?effect between the O-p and V-d orbitals. The bonding analysis revealed that the presence of V ?O ?enhances the covalency of the bonds ?（Li-O and V-O） of the two metal-doped systems. In the visible ?region ， Sn ?15 LiO ?32 ?and Sn ?15 VO ?32 ?had relatively high optical transparency. These results provided new ?ideas ?for the application of non-magnetic metal elements （Li）， magnetic metal elements （V）， and the corresponding point defects （V ?O /V ?Sn ） doped SnO ?2 ?in spintronic devices.

First-principles； Doped SnO ?2 ； Defects; Electronic structure； Magnetism； Optical property

1 引 言

稀磁半導體（Dilute Magnetic Semiconductor，DMS）是一種用金屬離子取代半導體中的一些非磁性陽離子而得到的新型半導體材料. 它也被稱為半磁性半導體或半導體自旋電子材料，是自旋電子學領域的關鍵材料 ?［1］ . 二氧化錫（SnO ?2 ）是一種重要的n型寬禁帶（ E ??g ?= 3.6 eV）半導體材料 ?［2］ ，具有低成本、優異的光學性能和高化學穩定性的優點，因而廣泛應用于太陽能電池、紫外激光器、發光二極管、特殊功能窗口涂層等光電器件領域 ?［3， 4］ ，是最具前景的新型材料之一.

然而，SnO ?2 的內部結構松散、密度低等缺點限制了其廣泛應用 ?［5］ . 摻雜是改善半導體材料性能最常見的方法之一. 通過摻雜金屬離子可以將SnO ?2 制成稀磁半導體 ?［6］ . 盡管先前的研究中獲得了一定的發現 ?［7-9］ ，但非磁性摻雜劑在誘導氧化物半導體中的鐵磁性能方面的作用仍未被完全了解. Rahman等人 ?［10］ 從理論上發現，鋰（Li）摻雜SnO ?2 可以作為自旋電子學的優質候選材料，因為Li作為一種自旋偏振器，在錫（Sn）位取代時誘導SnO ?2 顯磁性，而在占據氧（O）位和間隙位時不誘導SnO ?2 顯磁性. 在完美的SnO ?2 晶體中，Sn的價態為Sn ?4+ ，產生一個Sn空位（V ?Sn ）會帶來四個空穴，當Li ?1+ 引入Sn位時，它提供一個電子來補償一個空穴. 三個未補償的空穴局域在周圍的O原子上，此時超胞的磁矩為3 ?μ ?B ?［10］ . 對Li摻雜SnO ?2 系統也有一些實驗方面的研究：Srivastava等人 ?［11］ 發現，Li可以在低溫（3 K）下誘導特定濃度摻雜體系Sn ?1- ???x ?Li ??x ?O ?2 （0.03≤ x ≤0.09）呈現順磁性；Wang等人 ?［12］ 采用溶膠-凝膠法合成了摻Li的SnO ?2 納米顆粒，結果表明Li的取代摻雜可以增強SnO ?2 的鐵磁性，其中，Sn ?0.94 Li ?0.06 O ?2 納米顆粒的飽和磁化強度最大. 然而，Li在SnO ?2 中作為陽離子取代以及與點缺陷共同作用的機理尚不清楚.

另一方面，過渡金屬（TM）離子在SnO ?2 中具有較高的熱溶解度. 摻雜TM的SnO ?2 由于其室溫鐵磁性和良好的光學透明度，在制備自旋相關器件方面具有良好的的應用前景 ?［13， 14］ . 因此，許多研究主要集中在TM摻雜SnO ?2 上 ?［15， 16］ . 引人注意的是，磁性過渡金屬離子釩（V）摻雜對半導體的鐵磁性具有調控作用：Tahir等人 ?［17］ 采用溶膠凝膠法合成了V摻雜的氧化鋅納米顆粒，結果表明ZnO的飽和磁化強度隨V摻雜濃度（0%～8%）的增加而單調增加；Zhang等人 ?［18］ 在單步薄膜硫化方法生產的摻V二硫化鎢單層半導體中發現了鐵磁有序性. 盡管如此，對磁性過渡金屬離子V摻雜SnO ?2 的研究還不夠.

因此，為了研究非磁性/磁性金屬摻雜劑及點缺陷（V ?O /V ?Sn ）對二氧化錫基稀磁半導體 （SnO ?2 -DMS）的調控作用，本文通過第一性原理計算得到了其能帶結構、態密度（DOS）、電荷密度、Bader電荷、晶體軌道哈密頓布居（COHP）和光學性質. 在此基礎上，描述了不同摻雜方式對SnO ?2 的電子結構、磁性和光學性能的關系，為制備具有鐵磁性和優異光學性能的SnO ?2 -DMS的提供了理論指導.

2 計算方法和晶體結構模型

2.1 計算方法

本文采用自旋極化的密度泛函理論（DFT），離子實和價電子之間的相互作用通過投影綴加平面波的方法描述（PAW） ?［19］ ，電子之間的交換關聯能量采用 Perdew，Burke和 Ernzerhof 發展的廣義梯度近似（GGA）方法 ?［20］ 描述. 這種方法通過 Vienna ?ab initio ?Simulation Package （VASP）軟件包 ?［21， 22］ 實現. 傳統的GGA計算方法低估了d態的結合能，嚴重影響了帶隙 ?［23］ ，因此，所有的系統都使用GGA + ?U 方法來校正電子結構 ?［24］ . 有效原位庫倫能 U ?= ?U ??1 ?- ?J ??［25］ ，其中 J 是交換相互作用，設置為0.0 eV， U 是原位庫倫交換作用. 為了確保計算出的帶隙接近于SnO ?2 的實驗值，對Sn-d態和O-p態的U值進行了循環測試. ?U 值范圍（ U ??Sn， d ?= 0～7 eV和 U ??O， p ?= 0～10 eV）的確定是基于先前的文獻（Sn-d態的 U 值范圍為3.5～7.3 eV ?［26-28］ ，O-p態的 U 值為9.6 eV ?［29］ ）設置. 最終選擇 ?U 參數分別為 U ??O， p ?= 8.5 eV、 U ??Sn， d ?= 5.5 eV和 U ??V， d ?= 2.7 eV ?［29］ . 前期測試結果表明，7 × 7 × 10和3 × 3 × 5的 k 網格分別對原胞和超胞具有良好的能量收斂性. 能量的精度設置為1 × 10 ?-8 ?eV/原子，每個原子的力分別小于1 × 10 ?-5 ?eV/. 此外，進一步驗證了各個摻雜體系的熱穩定性，在正則系綜（Canonical Ensemble， NVT）中對各個摻雜體系的超胞（Sn ?60 Li ?4 O ?128 、Sn ?60 Li ?4 O ?124 、Sn ?56 Li ?4 O ?128 、Sn ?60 V ?4 O ?128 、Sn ?60 V ?4 O ?124 和Sn ?56 V ?4 O ?128 ）進行了從頭算分子動力學模擬（ Ab initio ?Molecular Dynamics，AIMD）. 在整個模擬過程中，超胞中的所有原子都可以自由移動. 所有的AIMD模擬都是在室溫（300 K）下進行了20 ps，時間步長為1 fs. 使用Bader程序 ?［30-32］ 進行Bader電荷分析，計算化合物每個原子中原子體積的總電荷. 為了研究鍵合性質，利用局部軌道基組向電子結構重建 （LOBSTER）程序 ?［33-35］ 進行了晶體軌道哈密頓布居（Crystal Orbital Hamilton Population，COHP） 和晶體軌道鍵合指數（Crystal Orbital Bond Index，COBI）分析，分析了VASP輸出的電子結構.

2.2 晶體結構模型

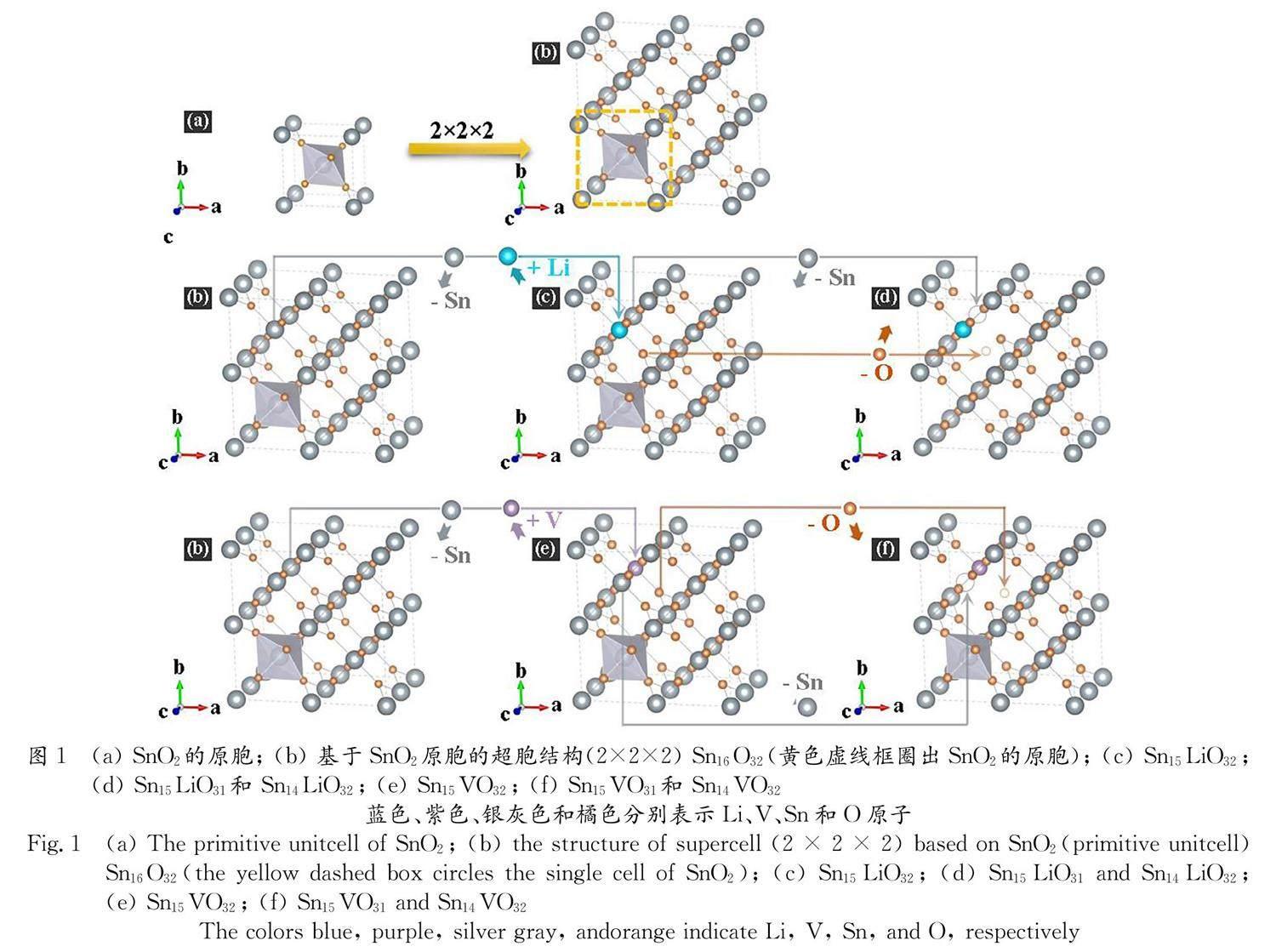
金紅石型SnO ?2 的原胞由6個原子（4個O原子和2個Sn原子）組成 ?［36］ （見圖1a）. 空間群為P ?42 /mm ?［37］ . 原胞沿著 x 、 y 和 z 向量方向擴展成一個2 × 2 × 2超胞 （Sn ?16 O ?32 ）. Sn ?16 O ?32 包含16個Sn原子和32個O原子（見圖1b）. 基于超胞 Sn ?16 O ?32 ?，考慮了以下模型來揭示不同摻雜方法對SnO ?2 性能的影響：（1） Li代替了Sn的位置，記為Sn ?15 LiO ?32 （見圖1c）. （2） 如圖1d所示，在Li代替了Sn的位置的基礎上，去掉一個O原子，記為Sn ?15 LiO ?31 ；去掉一個Sn原子，記為Sn ?14 LiO ?32 . （3） V代替了Sn的位置，記為Sn ?15 VO ?32 （見圖1e）. （4） 如圖1f所示，在V代替了Sn的位置的基礎上，去掉一個O原子，記為Sn ?15 VO ?31 ；去掉一個Sn原子，記為Sn ?14 VO ?32 .

3 結果和討論

3.1 結構穩定性分析

計算得到的七種體系的晶格參數和相應的摻雜濃度見表1. 其中，SnO ?2 的晶格常數為 a =4.6527 和 c =3.0867 與SnO ?2 實驗中的晶格參數（ a =4.7370 和 c =3.1870 ） ?［38］ 差別很小. 研究發現，當Li摻雜SnO ?2 薄膜達到15% ?［39］ 、V摻雜SnO ?2 薄膜的濃度達到6.7% ?［40］ 時，沒有發生相變. 因此，本文的最高摻雜濃度為6.25%，可以看作是合理的計算設置，并沒有改變SnO ?2 的金紅石結構.

根據以下公式 ?［41］ 計算了摻雜體系形成能（ E ??f ），以確定摻雜體系是否穩定：

E ?f =E ?d -E ?p -μ ??Li ?+μ ??Sn ?（1）

E ?f =E ?d -E ?p -μ ??Li ?+μ ??Sn ?+μ ?O （2）

E ?f =E ?d -E ?p -μ ??Li ?+2μ ??Sn ???（3）

E ?f =E ?d -E ?p -μ ?V +μ ??Sn ???（4）

E ?f =E ?d -E ?p -μ ?V +μ ??Sn ?+μ ?O （5）

E ?f =E ?d -E ?p -μ ?V +2μ ??Sn ?（6）

其中， E ??p 和 E ??d 分別為摻雜前后體系的總能量. ?μ ??Sn 、 μ ??Li 、 μ ??V 和 μ ??O ?是Sn、Li、V和O原子的孤立原子能量.

六種摻雜體系在不同條件下的形成能如圖2所示. Sn ?15 VO ?32 ?體系的形成能比Sn ?15 LiO ?32 ?低，說明V元素單摻雜體系比Li元素單摻雜體系更穩定. 當有點缺陷存在時，Li存在的三個摻雜體系的形成能大小排序為 Sn ?15 LiO ?3 ??1 ＞Sn ?15 LiO ?32 ＞Sn ?14 LiO ?32 ；V存在的三個摻雜體系的形成能大小排序為 Sn ?15 VO ?3 ??1 ＞Sn ?15 VO ?32 ＞Sn ?14 VO ?32 . 表明V ?O 的存在顯著降低了摻雜體系的形成能，而具有V ?Sn 的系統形成能最高、最不穩定.

除此之外，采用正則系綜（NVT）中的AIMD計算了超胞（Sn ?60 Li ?4 O ?128 、Sn ?60 Li ?4 O ?124 、Sn ?56 Li ?4 O ?128 、Sn ?60 V ?4 O ?128 、Sn ?60 V ?4 O ?124 和Sn ?56 V ?4 O ?128 ）的熱穩定性. 六個超胞體系的AIMD的結果見表2. 總能量、溫度和鍵長的小波動結果證明了摻雜系統（Sn ?60 Li 4O ?128 、Sn 60Li 4O ?124 、Sn ?56 Li 4O ?128 、Sn ?60 V 4O ?128 、Sn ?60 V ?4 O ?124 和Sn ?56 V ?4 O ?128 ）在300 K下具有高的熱穩定性.

3.2 磁性分析

從圖3中的磁矩圖可以看出，純SnO ?2 不具有磁性，但摻雜體系具有顯著的磁性. 比較體系Sn ?15 LiO ?32 和Sn ?15 VO ?32 ，可以發現Li對摻雜體系磁矩的影響大于V. 當有點缺陷存在時，V ?Sn 可以顯著提高了摻雜體系的磁性，而V ?O 在Li摻雜體系和V摻雜體系中發揮著截然相反的作用：當V ?O 存在于Li摻雜體系時，體系磁矩降低；當V摻雜體系中有V ?O 存在，體系磁矩增大. 總的來說，摻雜體系的磁矩是整數，說明摻雜體系具有鐵磁性 ?［42］ . 這為提高SnO ?2 -DMS的磁性提供了新的啟迪.

為了直觀地分析摻雜體系的磁性，繪制了凈自旋電荷密度圖如圖4所示，其中黃色電子云表示自旋向上，藍色電子云表示自旋向下. 可以看出， 圖4a 中Sn ?15 LiO ?32 的磁性主要是由Li原子周圍的O原子自旋極化引起的. 當V ?O 存在時，Sn ?15 LiO ?31 （圖4b）中Li原子周圍的O原子自旋極化減少，因此磁矩降低為3 ?μ ??B . 當V ?Sn 存在時，Sn ?1 ??4 LiO ?3 ??2 （圖4c）的磁性不僅來源于Li原子周圍的O原子自旋極化，同時V ?Sn 原子周圍的O原子自旋極化也增加了磁性，因此磁矩增大為7 ?μ ??B . 圖4d中Sn ?15 VO ?32 的磁性主要是由V原子自旋極化引起的. 當V ?O 存在時，Sn ?15 VO ?31 （圖4e）的磁性不僅來源于V原子自旋極化，同時V ?O 周圍的O原子的自旋極化也增加了磁性，因此磁矩增大為3 ?μ ??B . 當V ?Sn 存在時，在Sn ?14 VO ?32 （圖4f）中，V ?Sn 周圍的O原子自旋極化導致了正的電子云，V原子的自旋極 化導致了負的電子云，使得體系的磁矩為4 ?μ ??B . 因此，點缺陷對Li元素摻雜SnO ?2 和V元素摻雜SnO ?2 的磁性影響不同.

采用幾何優化后的晶體結構，計算了七個體系的能帶結構和態密度（Density of States，DOS），如圖5（Sn ?16 O ?32 ，Sn ?15 LiO ?32 ，Sn ?15 LiO ?3 ??1 和Sn ?1 ??4 LiO ?32 ）和圖6（Sn ?16 O ?32 ，Sn ?15 VO ?32 ，Sn ?15 VO ?3 ??1 ，和Sn ?1 ??4 VO ?32 ）所示. 圖5a和圖6a顯示出Sn ?16 O ?32 的帶隙值為3.25 eV. 帶隙比實驗中的帶隙（3.60 eV） ?［43］ 要小. 這是因為GGA函數不能精確地描述電子之間的強相關相互作用. 通過計算摻雜前后SnO ?2 的平均靜電勢（Average Electrostatic Potential， V ??av ）并選擇遠離缺陷位置的原子的 V ??av 來調整六種摻雜系統的費米能級. 雖然本文計算的帶隙比實驗值略窄，但是對后續的性能分析幾乎沒有影響. 如圖5和圖6c、6e和6g的能帶圖所示，摻雜后體系的能帶變得致密，在費米能級上下產生了雜質能級，對應DOS圖可以看出：Li的三個摻雜體系（圖5d、5f和5h）的費米能級由O-p和Li-s軌道貢獻；V的三個摻雜體系（圖6d、6f和6h）的費米能級由O-p和V-d軌道貢獻. 摻雜后的帶隙都有不同程度的減小：圖5中摻雜體系帶隙的大小排列順序為Sn ?15 LiO ?31 （1.33 eV）＞Sn ?15 LiO ?3 ??2 （1.03 eV）＞ Sn ?14 LiO ?3 ??2 ?（0.00 eV）；圖6中摻雜體系帶隙的大小排列順序為Sn ?15 VO ?3 ??2 （2.14 eV）＞Sn ?15 VO ?3 ??1 （0.98 eV）＞Sn ?1 ??4 VO ?3 ??2 （0.00 eV）. 在Li的三個摻雜體系中，O-p和Li-p軌道的相互作用使導帶向下移動，O-p、Sn-p、和Li-p軌道的相互作用是價帶向上移動，使帶隙變窄. 在V的三個摻雜體系中，O-p和V-d軌道的相互作用使導帶向下移動，O-p、Sn-p、和V-d軌道的相互作用是價帶向上移動，使帶隙變窄. 如圖5中的DOS所示，在不對稱的O-p和Li-p軌道之間存在著明顯的耦合. 這證實了Li摻雜體系的磁性是由O-p和Li-p軌道之間的電子交換相互作用產生的. 從圖6中的DOS中可以看出，在不對稱的O-p和V-d軌道之間存在著明顯的耦合. 這證實了V摻雜體系的磁性是由O-p和V-d軌道之間的電子交換相互作用產生的. 這一現象可以用 Ruderman-Kittel-Kasuya-Yosida （RKKY） ?［44］ 中以載體作為橋梁的雙交換效應來解釋. 在摻雜體系中，作為載體的載流子其能帶形成與鍵長、鍵角密切相關，三者關系如下 ?［45］ .

W∝ ?cos ??1 2 ??π -θ ??d ??3 ?.5 ????B - l ????（7）

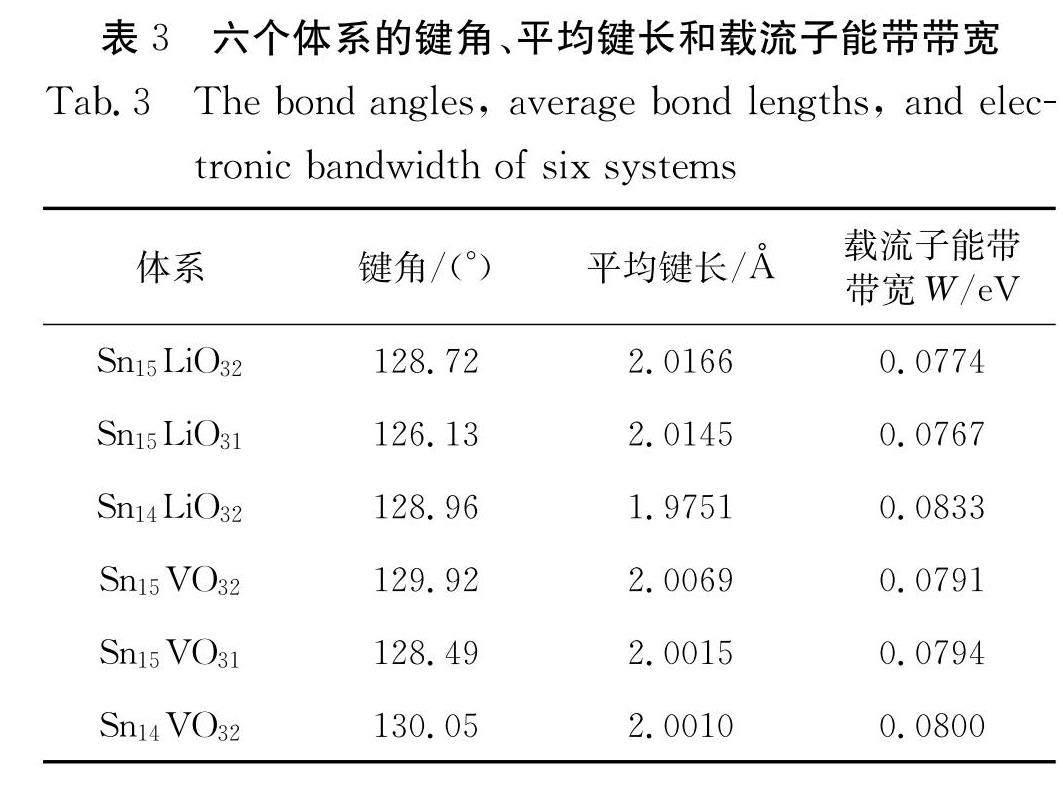
其中， d ??B-l 是 X -O的平均鍵長（ X =Li， V， Sn）; θ 是 Y -O-Sn之間的鍵角（ Y =Li， V）; W 是載流子能帶的帶寬. ?W 值越大， X 原子和O原子軌道的交疊范圍越大，有利于載流子在 Y -O-Sn網格中巡游，即增強了雙交換作用. 如表3所示，三個Li摻雜體系中，Sn ?14 LiO ?32 ?的 W 值最大，O-p和Li-p軌道之間的電子交換相互作用最大，因此磁矩最大（ 7 ?μ ??B ?）；三個V摻雜體系中，Sn ?14 VO ?32 ?的 W 值最大，V-d和O-p軌道之間的電子交換相互作用最大，因此磁矩最大（4 ?μ ??B ）.

3.3 鍵的穩定性分析

為了研究摻雜體系中原子間的相互作用和鍵合狀態，七個體系在（110）平面上的相鄰原子的鍵長如圖7所示. 同時，圖8a和圖9a是Sn ?16 O ?32 -（110）表面的電荷密度 （以e/Bohr ?3 為單位），圖 8b～8d 和圖9b～9d是分別是Li摻雜體系和V摻雜體系在（110）表面上的差分電荷密度（與 Sn ?16 O ?32 ?-（110）表面的電荷密度做差）. 此外，為了定量地表示相應原子的電荷轉移，對Bader電荷的分析結果展示在圖10中.

與圖7a中Sn ?16 O ?32 -（110）表面的Sn ?3 -O ?4 和Sn ?3 -O ?6 的鍵長相比，摻雜Li后，Sn ?15 LiO ?32 （圖7b）中相同位置的Li-O ?4 和Li-O ?6 變長. 當有V ?O 存在時，Sn ?15 LiO ?31 （圖7c）中的Li-O ?6 比Sn ?15 LiO ?32 中的Li-O ?6 短；當有V ?Sn 存在時，Sn ?14 LiO ?32 （圖7d）中的Li-O ?3 和Li-O ?5 比Sn ?15 LiO ?32 中的Li-O ?4 和Li-O ?6 長. Li的三個摻雜體系中，Li-O ?6 的鍵長順序為：Sn ?1 ??4 LiO ?32 ＞Sn ?15 LiO ?32 ＞Sn ?15 LiO ?31 . 在差分電荷密度（圖8b～8d）可以看出， 三個摻雜體系中Li周圍的電子減少，對應Bader電荷轉移 （圖10b～10d）可以看出，Li失去的電子數順序為：Sn ?14 LiO ?32 （-0.78 e ）＞Sn ?15 LiO ?32 （-0.65 e）＞Sn ?15 LiO ?31 （-0.40 e）.

與圖7a中Sn ?16 O ?32 -（110）表面的Sn ?2 -O ?3 和Sn ?2 -O ?5 的鍵長相比，摻雜V后，Sn ?15 VO ?32 （圖7e）中相同位置的V-O ?3 和V-O ?5 變短. 當有V ?O 存在時，Sn ?15 VO ?31 （圖7c）中的V-O ?5 比Sn ?15 VO ?32 中的V-O ?5 短；當有V ?Sn 存在時，Sn ?14 VO ?32 （圖7d）中的V-O ?3 和V-O ?5 比Sn ?15 VO ?32 中的V-O ?3 和V-O ?5 長. V的三個摻雜體系中，V-O ?5 的鍵長順序為：Sn ?14 VO ?32 ＞ ??Sn ?15 VO ?32 ?＞Sn ?15 VO ?31 . 在差分電荷密度（圖9b～9d）可以看出， 三個摻雜體系中V周圍的電子減少，對應Bader電荷轉移（圖10e～10g）可以看出，V失去的電子數順序為：Sn ?14 VO ?32 （-3.66 e）＞Sn ?15 VO ?32 （-2.34 e）＞Sn ?15 VO ?31 （-0.67 e）.

為了研究摻雜體系原子間的鍵合狀態，采用LOBSTER程序對Sn-O、Li-O和V-O鍵進行了COHP分析. 在圖11和圖12中，將COHP表示為負值（-COHP），所以線下面積的正負值分別對應成鍵態和反鍵態. 在圖11a、11b和圖12a、12b中，Sn-O鍵在0～-10 eV的能量范圍內表現為成鍵狀態，這主要是由于Sn-p和O-p的重疊和雜交造成的. Sn-p和O-p的反鍵態和成鍵態分布在費米能級兩側，表明Sn-O鍵具有共價性質. 與圖11d Sn ?15 LiO ?32 ?的Li-O ?6 鍵相比，圖11e Sn ?15 LiO ?31 的Li-O ?6 鍵比較強，這與Li-O ?6 的鍵長變短分析相一致. 與圖11d Sn ?15 LiO ?32 的Li-O ?6 鍵相比，圖11g Sn ?14 LiO ?32 的Li-O ?6 鍵比較弱，這與Li-O ?6 的鍵長變長分析相一致. 表4中列出了各個鍵的COBI積分值（ICOBI），ICOBI值越大，表示鍵的共價性更強. 可以看出，Li的三個摻雜體系的ICOBI順序為：Li-O ?6 ?（2）＞Li-O ?6 ?（1）＞Li-O ?6 ?（3）. 因此，非磁性金屬元素Li摻雜的體系中，V ?O 的存在可以提高Li-O鍵的共價性，而V ?Sn 的存在會降低Li-O鍵的共價性. 與圖11d Sn ?15 VO ?32 ?的V-O ?6 鍵相比，圖12e Sn ?15 VO ?31 的V-O ?5 鍵比較強，這與V-O ?6 的鍵長變短分析相一致. 與圖12d Sn ?15 VO ?32 ?的V-O ?5 鍵相比，圖12g Sn ?14 VO ?32 的V-O ?5 鍵比較弱，這與V-O ?5 的鍵長變長分析相吻合. 可以從表4看出，V的三個摻雜體系的ICOBI順序為：V-O ?5 ?（2）＞V-O ?5 ?（1）＞V-O ?5 ?（3）. 因此，磁性金屬元素V摻雜的體系中，V ?O 的存在可以提高V-O鍵的共價性，而V ?Sn 的存在會降低V-O鍵的共價性.

3.4 光學性質

DMS在可見光范圍內的性能對自旋電子器件的應用也非常重要. 為了理解半導體的宏觀光學性質，用以下公式來表示復介電函數.

ε=ε 1（ω）+ε 2（ω） ?（8）

其中， ε ??1 （ ω ）和 ε ??2 （ ω ）分別為復介電函數的實部和虛部. 上述方程中復介電函數的實部［ ε ??1 （ ω ）］和虛部［ ε ??2 （ ω ）］可以由Kramers-Kronig的色散關系推導出來 ?［46］ . 光吸收率 α （ ω ）和光反射率 R （ ω ）可以通過 ε ??1 （ω）和 ε ??2 （ω）獲得，公式如下 ?［47］ ：

ε 1（ω）= 2 e ?ε 0m 2 ∑ ??C，V ??∫ ?BZ ???d K ?α·M ?C，V （K） ??2 ? 2 π ?2 ?E C（K）-E V（K） ??2 ×

2-ω 2 ???E C（K）-E V（K） ??????2 ?+1 ?（9）

ε 2（ω）= π ε 0 ????e ?mω ???2∑ ??C，V ??∫ ?BZ ???d K 2π 2 ??α·M ?C，V （K） ??2×

δ E C（K）-E V（K）- ?ω ??（10）

α（ω）= 2 ω ??ε 2 1（ω）+ε 2 2（ω） -ε 1（ω） ????1 2 ???（11）

R（ω）= ???ε 2 1（ω）+jε 2（ω） -1 ?ε 2 1（ω）+jε 2（ω） +1 ???2 ?（12）

其中， ω 為角頻率; ?E ??C （ K ）和 E ??V （ K ）為導帶和價帶的固有能級，對應的C和V分別表示導帶和價帶; ?M ??C，V （ K ）為過渡矩陣元素.

圖13展示了各個體系的吸收和反射光譜，這有助于研究非磁性金屬元素（Li）和磁性金屬元素（V）及相應的點缺陷（V ?O /V ?Sn ）對SnO ?2 體系光學性能的影響. 圖13a和13b顯示純SnO ?2 的光吸收邊緣約為3.5 eV，結合圖5a、5b中的電子結構可以推斷，電子從價帶的O-p態到導帶的Sn-p態的躍遷導致了純SnO ?2 系統在紫外區域的吸收峰（5～ 6 eV ）. 摻雜后的體系的光吸收邊緣向較低的能量方向移動（紅移現象）. 這是因為摻雜引起費米能級附近出現了雜質能級，并使導帶朝較低的能級移動，從而助于電子從雜質能級到導帶底部的遷移. 六個體系的吸收光譜顯示，Sn ?14 LiO ?32 和Sn ?14 VO ?32 在紅外區出現了明顯的吸收峰. 對比圖5g、5h和圖6g、6h的電子結構圖可以看出，Sn ?14 LiO ?32 和Sn ?14 VO ?32 都產生了新的雜質能級，體系帶隙變成0.0 eV，在Sn ?14 LiO ?32 中，電子從Li-p態躍遷到O-p態，在Sn ?14 VO ?32 中，電子從V-d態躍遷到O-p態. 相對于SnO ?2 體系，所有摻雜體系的光吸收和光反射率都有所增加. 其中，Sn ?15 LiO ?32 和Sn ?15 VO ?32 在可見光區域中的光吸收和光反射率最低.

依據一般的有效輻射分布公式，如下：

τ+R+α=1 ?（13）

其中， τ 、 R 和 α 分別為光學透明度、光學反射率和光吸收率. 從公式（13）可以判斷出Sn ?15 LiO ?32 和Sn ?15 VO ?32 在可見光區域具有較高的光學透明度.

4 結 論

綜上所述，本文詳細地研究了非磁性金屬元素（Li）和磁性金屬元素（V）及相應的點缺陷（V ?O /V ?Sn ）摻雜對SnO ?2 的電子結構和磁、光學性質. 研究表明，一方面，V元素單摻雜體系比Li元素單摻雜體系更穩定. 當有點缺陷存在時，V ?O 顯著提升了摻雜體系的穩定性，而V ?Sn 會降低摻雜體系的穩定性. 另一方面，Li對摻雜體系磁矩的影響大于V. 當有點缺陷存在時，V ?Sn 的加入顯著提高了摻雜體系的磁性，而V ?O 對V摻雜體系的磁性提升有益，卻顯著地降低了Li摻雜體系的磁性. Li摻雜體系的磁性是由O-p和Li-p軌道之間的電子雙交換作用產生的；V摻雜體系的磁性是由O-p和V-d軌道之間的電子雙交換作用產生的. 鍵合分析表明，Li摻雜的體系中，V ?O 的存在可以提高Li-O鍵的共價性，而V ?Sn 的存在會降低Li-O鍵的共價性；V摻雜的體系中，V ?O 的存在可以提高V-O鍵的共價性，而V ?Sn 的存在會降低V-O鍵的共價性. 在可見光區域內，Sn ?15 LiO ?32 和Sn ?15 VO ?32 具有較高的光學透明度. 總之，本文對非磁性金屬元素（Li）和磁性金屬元素（V）及相應的點缺陷（V ?O /V ?Sn ）摻雜SnO ?2 的研究可以幫助指導具有鐵磁性和優異光學性能的SnO ?2 -DMS材料的制備.

參考文獻：

［1］ ??Ohno H. Making nonmagnetic semiconductors ferromagnetic ［J］. Science， 1998， 281： 951.

［2］ ?Sang-Hun N， Jin-Hyo B. Rutile structured SnO ?2 ?nanowires synthesized with metal catalyst by thermal evaporation method ［J］. J Nanosci Nanotechnol， 2012， 12： 1559.

［3］ ?Xiong L B， Qin M C， Chen C， ?et al . Fully high-temperature-processed SnO ?2 ?as blocking layer and scaffold for efficient， stable， and hysteresis-free mesoporous perovskite solar cells ［J］. Adv Funct Mater， 2018， 28： 1706276.

［4］ ?Lavanya N， Sekar C， Fazio E， ?et al . Development of a selective hydrogen leak sensor based on chemically doped SnO ?2 ?for automotive applications ［J］. Int J Hydrogen Energy， 2017， 42： 10645.

［5］ ?Das S， Jayaraman V. SnO ?2 ： a comprehensive review on structures and gas sensors ［J］. Prog Mater Sci， 2014， 66： 112.

［6］ ?Yan W S， Liu Q H， Wang C， ?et al . Realizing ferromagnetic coupling in diluted magnetic semiconductor quantum dots ［J］. J Am Chem Soc， 2014， 136： 1150.

［7］ ?Peng H W， Xiang H J， Li S S， ?et al . Origin and enhancement of hole-induced ferromagnetism in first-row ?d ??0 ?semiconductors ［J］. Phys Rev Lett， 2009， 102： 017201.

［8］ ?Delgado F P， Vasquez F C， Holguín-Momaca J T， ?et al . Room-temperature ferromagnetism and morphology evolution of SnO ?2 ［J］. J Magn Magn Mater， 2019， 476： 183.

［9］ ?Ahmed A， Siddique M N， Ali T， ?et al . Defect assisted improved room temperature ferromagnetism in Ce doped SnO ?2 ?nanoparticles ［J］. Appl Surf Sci， 2019， 483： 463.

［10］ ?Rahman G， Din N U. Stabilizing intrinsic defects in SnO ?2 ［J］. Phys Rev B， 2013， 87： 205205.

［11］ Srivastava S K， Lejay P， Hadj-Azzem A， ?et al . Non-magnetic impurity induced magnetism in Li-doped SnO ?2 ?nanoparticles ［J］. J Supercond Nov Magn， 2014， 27： 487.

［12］ Wang N， Zhou W， Wu P. Ferromagnetic spin-order in SnO ?2 ?nanoparticles with nonmagnetic Li doping ［J］. J Mater Sci： Mater Electron， 2015， 26： 4132.

［13］ Lamrani A F. Ferromagnetic alloy for high-efficiency photovoltaic conversion in solar cells： first-principles insights when doping SnO ?2 ?rutile with coupled EuGd ［J］. RSC Adv， 2021， 11： 7096.

［14］ Xu J， Mu Y K， Ruan C H， ?et al . S or N-monodoping and S， N-codoping effect on electronic structure and electrochemical performance of tin dioxide： simulation calculation and experiment validation ［J］. Electrochim Acta， 2020， 340： 135950.

［15］ Zhuang S D， Xu X Y， Pang Y R， ?et al . Variation of structural， optical and magnetic properties with Co-doping in Sn ?1 ??- ???x ?co ??x ?O ?2 ?nanoparticles ［J］. J Magn Magn Mater， 2013， 327： 24.

［16］ Jaiswal ?M K， Kumar R， Kanjilal D. Studies of dense electronic excitation induced modification in crystalline Fe doped SnO ?2 ?thin films ［J］. Appl Surf Sci， 2015， 332： 726.

［17］ Tahir N， Hussain S T， Usman M， ?et al . Effect of vanadium doping on structural， magnetic and optical properties of ZnO nanoparticles ［J］. Appl Surf Sci， 2009， 255： 8506.

［18］ Zhang F， Zheng B Y， Sebastian A， ?et al . Monolayer vanadium-doped tungsten disulfide： a room-temperature dilute magnetic semiconductor ［J］. Adv Sci， 2020， 7： 2001174.

［19］ Blchl P E. Projector augmented-wave method ［J］. Phys Rev B， 1994， 50： 17953.

［20］ Kresse G， Furthmüller J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set ［J］. Comput Mater Sci， 1996， 6： 15.

［21］ Kresse G， Furthmüller J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set ［J］. Phys Rev B， 1994， 54： 11169.

［22］ Perdew J P， Burke K， Ernzerhof M. Generalized gradient approximation made simple ［J］. Phys Rev Lett， 1996， 77： 3865.

［23］ Anisimuv V I， Zaanen J， Andersen O K. Band theory and Mott insulators： Hubbard ?U ?instead of stoner ?I ?［J］. Phys Rev B， 1991， 44： 943.

［24］ CePerley D M， Alder B G. Ground state of the electron gas by a stochastic method ［J］. Phys Rev Lett， 1980， 45： 566.

［25］ Gu J X， Jin K J， Ma C， ?et al . Coexistence of polar distortion and metallicity in PbTi ?1- ???x ?Nb ??x ?O ?3 ［J］. Phys Rev B， 2017， 96： 165206.

［26］ Singh A K， Janotti A， Scheffler M， ?et al . Sources of electrical conductivity in SnO ?2 ［J］. Phys Rev Lett， 2008， 101： 055502.

［27］ Villamagua L， Stashans A， Carini M， ?et al . Doping of SnO ?2 ?with H atoms： an alternative way to attain ?n -type conductivity ［J］. AIP Adv， 2016， 6： 115217.

［28］ Faudoa-Arzate ?A， Camarillo-Cisneros J， Castillo-González A R， ?et al . Disinfection mechanism of the photocatalytic activity of SnO ?2 ?thin films against Candida albicans， proposed from experimental and simulated perspectives ［J］. Can J Microbiol， 2021， 67： 667.

［29］ Akbar W， Elahi I， Nazir S. Development of ferromagnetism and formation energetics in 3 d ?TM-doped SnO ?2 ： GGA and GGA + ?U ?calculations ［J］. J Magn Magn Mater， 2020， 511： 166948.

［30］ Henkelman G， Arnaldsson A， Jónsson H. A fast and robust algorithm for Bader decomposition of charge density ［J］. Comput Mater Sci， 2006， 36： 354.

［31］ Sanville E， Kenny S D， Smith R， ?et al . Improved grid-based algorithm for Bader charge allocation ［J］. J Comput Chem， 2007， 28： 899.

［32］ Tang ?W， Sanville E， Henkelman G. A grid-based Bader analysis algorithm without lattice bias ［J］. J Phys： Condens Matter， 2009， 21： 084204.

［33］ Deringer V L， Tchougréeff A L， Dronskowski R. Crystal orbital Hamilton population （COHP） analysis as projected from plane-wave basis sets ［J］. J Phys Chem A， 2011， 115： 5461.

［34］ Dronskowski R， Bloechl P E. Crystal orbital Hamilton populations （COHP）： energy resolved visualization of chemical bonding in solids based on density-functional calculations ［J］. J Phys Chem， 1993， 97： 8617.

［35］ Maintz S， Deringer V L， Tchougréeff A L， ?et al . LOBSTER： a tool to extract chemical bonding from plane-wave based DFT ［J］. J Comput Chem， 2016， 37： 1030.

［36］ Hassan F E H， Moussawi S， Noun W， ?et al . Theoretical calculations of the high-pressure phases of SnO ?2 ［J］. Comput Mater Sci， 2013， 72： 86.

［37］ Haines J， Léger J M. X-ray diffraction study of the phase transitions and structural evolution of tin dioxide at high pressure： Relationships between structure types and implications for other rutile-type dioxides ［J］. Phys Rev B， 1997， 55： 11144.

［38］ Thangaraju B. Structural and electrical studies on highly conducting spray deposited fluorine and antimony doped SnO ?2 ?thin films from SnCl ?2 ?precursor ［J］. Thin Solid Films， 2002， 402： 71.

［39］ Wang J C， Zhou W， Wu P. Band gap widening and d ?0 ?ferromagnetism in epitaxial Li-doped SnO ?2 ?films ［J］. Appl Surf Sci， 2014， 314： 188.

［40］ Hong N H， Sakai J. Ferromagnetic V-doped SnO ?2 ?thin films ［J］. Physica B： Condens Matter， 2005， 358： 265.

［41］ Ghosh ?S， Khan G G， Mandal K. Defect-driven magnetism in luminescent ?n / p -type pristine and Gd-substituted SnO ?2 ?nanocrystalline thin films ［J］. ACS Appl Mater Interfaces， 2012， 4： 2048.

［42］ Pickett W E， Moodera J S. Half metallic magnets ［J］. Phys Today， 2001， 54： 39.

［43］ Batzill M， Diebold U. The surface and materials science of tin oxide ［J］. Prog Surf Sci， 2005， 79： 47.

［44］ Jonker G H， Santen J H V. Ferromagnetic compounds of manganese with perovskite structure ［J］. Physica， 1950， 16： 337.

［45］ Radaelli P G， Iannone G， Marezio M， ?et al . Structural effects on the magnetic and transport properties of perovskite A ?1 ??- ???x ?A ??x ?MnO ?3 ?（ x ?= 0.25， 0.30） ［J］. Phys Rev B， 1997， 56： 8265.

［46］ Kronig R de L. On the theory of dispersion of ?x -rays ［J］. J Opt Soc Am， 1926， 12： 547.

［47］ Sun J， Wang H， He J， ?et al . ?Ab initio ?investigations of optical properties of the high-pressure phases of ZnO ［J］. Phys Rev B， 2005， 71： 125132.