強化思維教學 落實核心素養（一）

章建躍

一、總體評價

本次活動堅持以習近平新時代中國特色社會主義思想為指導，全面貫徹黨的教育方針，落實立德樹人根本任務.

本次活動全面落實育人方式改革任務，著眼優化教學方式，強化課堂教學主陣地作用，提升學生課堂學習效率，切實減輕學生過重的課業負擔，提升課堂教學質量.

本次活動根據深化課程改革推進育人方式變革的新要求，聚焦當前新課程標準、新教材、新高考改革中的熱點和難點問題積極探索、大膽創新，特別是在數學基本思想、基本活動經驗、發現和提出問題的能力、綜合實踐活動等方面開展深入研究與實踐，涌現了一批具有示范意義的課例.

本次活動展示的課例注重把握數學內容的本質，努力發揮數學學科獨特的育人價值，加強單元教學設計基礎上的課時教學設計研究，體現數學的整體性、邏輯的連貫性、思想的一致性、方法的普適性、思維的系統性，積極探索基于情境和問題導向的互動式、啟發式、探究式、體驗式等課堂教學，努力創設恰當的情境，提出合適的數學問題，引導學生開展系列化數學活動，通過積極主動的數學思考和交流，獲得“四基”、提高“四能”，從而使數學核心素養落實在課堂教學中.

本次活動展示的課例堅持教學相長，努力做到“該講的講清楚，該放的放到位”. 注重講清重點和難點，通過先行組織者、課堂小結等各種方式幫助學生構建知識體系，引導學生主動思考、積極提問、自主探究.

本次活動展示的課例融合運用傳統與現代技術手段，重視情境教學；積極探索基于數學學科的課程綜合化教學，大膽開展研究型、項目化、合作式學習. 精準分析學情，重視差異化教學和個別化指導.

本次活動取得預期效果，必將有力推動我國高中數學教育教學改革的深入發展.

二、本次活動的一些特點

1. 聚焦重點、難點課題，提供典型豐富課型

本次活動的課型非常豐富，有起始課、概念課、 性質課、公式法則課、練習課、試卷講評課、數學推理課（探究數學內部問題的綜合實踐活動課）、數學建模課（用數學解決現實問題的綜合實踐活動課）等.

本次活動有16節“概率與統計”相關課例. 指定課題注重在發展學生數學核心素養上有較大意義的、體現教育信息化要求的、普遍存在教學疑難的選題，并考慮函數、幾何與代數、概率與統計、數學建模活動與數學探究活動的內容平衡.

2. 單元-課時教學設計的理念深入人心

本次活動展示課例的教學設計比較好地體現了中國教育學會中學數學教學專業委員會（以下統稱“中數專委會”）頒發的“標準”的要求，課例按照“教學內容解析”“教學目標設置”“學生學情分析”“教學策略分析”“教學過程設計”五維度框架，或按照“內容和內容解析”“目標和目標分析”“教學問題診斷”“教學媒體設計”“教學過程設計”“目標檢測設計”六維度框架進行設計，使教學設計質量得到了基本保證.

此外，本次活動展示的課例按照“單元設計基礎上的課時教學設計”進行教學設計，追求從“四基”“四能”到數學核心素養的教學結果. 通過教學設計，幫助學生掌握核心知識，領悟內容蘊含的數學思想和方法，感悟用數學的方式觀察、思考與表達，學會有邏輯地思考，發展理性思維. 同時，教學設計注重學習結果的可遷移性，舉一反三、觸類旁通；解決數學內外問題，在綜合實踐活動中形成數學核心素養.

3. 明確基本套路，增強數學整體性

數學課程內容的一大特點是整體性，這種整體性主要表現在如下幾個方面.

（1）同一主題內容中體現的數學整體性——縱向聯系，主要包括一個內容的不同認知層次、不同角度認識之間內在的一致性和關聯性，以及認識不同方面內容所采用的類似過程與思想方法.

（2）具有內在聯系的不同內容之間的實質性關聯所體現的數學整體性——橫向聯系.

（3）不同領域的融合所體現的整體性——綜合貫通，主要是幾何與代數之間的融合，體現了不同數學思想與方法之間的融合，形成具有統一性、內在一致性的數學一般觀念，這是在最高層面上體現的數學整體性，其統攝性最強、適用性最廣.

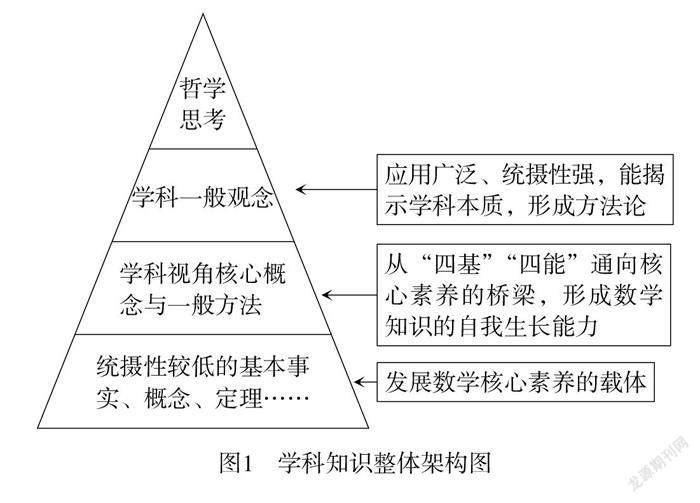
學科知識整體架構如圖1所示.

4. 發揮一般觀念引領作用，提升課堂教學品位

所謂一般觀念，是對內容及其反映的數學思想和方法的進一步提煉和概括，是對數學對象的定義方式有哪些、幾何性質指什么、代數性質指什么、函數性質指什么、概率性質指什么等問題的一般性回答，是研究數學對象的方法論，對學生學會用數學的方式對事物進行觀察、思考、分析，以及發現和提出數學問題等都具有指路明燈的作用.

能自覺運用一般觀念指導數學學習與探究活動是實現從“知其然”到“知其所以然”再到“何由以知其所以然”跨越的表現，是理性思維得到良好發展的表現，也是學生學會學習的標志.

5. 學生主體意識進一步加強

本次活動展示的課例，注重創設體現數學知識發生發展需要、數學與生活聯系的情境，使學生感悟數學知識產生的必然性；注重精心設計學生活動，采取問題引導學習的方式，讓學生帶著問題開展探索活動，將轉變學生的學習方式落在實處.

本次活動展示的課例普遍采用啟發式、互動式、探究式教學，注重學生參與，讓學生有主動學習的機會，教師采用追問的方式推動學生的數學理解.

6. 以邏輯連貫、具有思維挑戰性的問題串引導學生開展系列化數學學習活動

問題的水平體現了思維教學的水平，高水平的問題存在以下要點.

（1）反映當前學習內容的本質.

（2）在學生思維的最近發展區內，對學生的思維形成挑戰性——“窗戶紙”不能捅破.

（3）具有可發展性，形成系列問題.

（4）具有可模仿性，實現從“問題引導學習，激發學生思維”到“學生自主提問，展開創新學習”的過渡.

在理解數學、理解學生的基礎上才能提出高水平的問題.

7. 遵循概念認知規律，經歷完整學習過程

注重遵循認知心理學關于概念獲得的相關理論，普遍注重以概念形成的方式安排學習過程，完成“情境與問題—共性分析與歸納—抽象本質特征、下定義—關鍵詞辨析—簡單應用—聯系與綜合”的過程，讓學生在觀察與實驗、分析與綜合、歸納與概括中經歷概念的抽象過程，把數學抽象、直觀想象等核心素養滲透其中.

引入的必要性、概念抽象的過程性得到比較好的體現.

8. 定理、法則、公式等注重自主發現

教學設計中，在“如何使學生想得到”上下了較多的功夫，力爭通過問題情境促使學生實現自主發現. 例如，本次活動的指定課題，都要求通過恰當的問題情境引導學生自主發現，使學生發現和提出問題成為必然而不是“撞大運”.

9. 展示教師表現良好

展示教師充分準備，克服了許多困難，高質量、圓滿地完成了指定課題和展示任務.

在本次活動中，參加展示的教師都表現出很強的親和力，自然大方，有激情. 課堂氣氛比較生動活潑，教學效果普遍較好. 對“錄像課展示與自述”到底“展示”什么、“自述”什么，理解到位的教師也在增加，各地區教師間的差異越來越不明顯.

10. 學術委員工作認真負責

為了做好點評工作，各小組建立了學術委員微信群，多次召開專家組會議. 通過微信群明確點評任務，研討點評工作，形成共識.

本次活動線上舉行，遇到各種不熟悉的技術問題，大家群策群力，相互幫助，在中國教師研修網的強大技術力量支持下，圓滿解決問題，為大會直播奠定了良好的基礎.

學術委員們事先觀看了完整的課堂錄像，預先寫好了點評提綱，并做好PPT，再結合選手的現場表現給予認真點評. 點評效果很好，得到了廣大教師的普遍好評.

部分學術委員克服身體不適，堅持工作，非常令人感動.

三、今后需要努力的一些方面

1. 深刻認識數學的育人價值：不僅僅是為了分數和升學

數學在形成人的理性思維、科學精神和促進個人智力發展的過程中發揮著不可替代的作用. 數學素養是現代社會每個人應該具備的基本素養. 數學教育承載著落實立德樹人根本任務、發展素質教育的功能. 數學教育幫助學生掌握現代生活和進一步學習所必需的數學知識、技能、思想和方法；提升學生的數學素養，引導學生會用數學眼光觀察世界、會用數學思維思考世界、會用數學語言表達世界（以下統稱“三會”）；促進學生思維能力、實踐能力和創新意識的發展，探尋事物變化規律，增強社會責任感；在學生形成正確的人生觀、價值觀和世界觀等方面發揮著獨特的作用.

2. 將育德和育智統一在課堂教學中

以數學知識技能為載體，創設符合學生認知規律的問題情境，引導學生開展獨立思考、自主探究、合作交流，獲得“四基”，提高“四能”，形成數學的思維方式，培養理性思維和科學精神.

要防止貼標簽式德育，防止庸俗化德育，體現數學學科的育人特點，用數學的方式育人才有力量.

3. 大力加強思維教學

林崇德先生認為，在核心素養的文化基礎方面有兩個問題，一個是人文底蘊，一個是科學精神. 人文底蘊與科學精神是核心素養中的兩大素養，其中的關鍵是思維教學. 其中，科學精神包括理性思維、質疑批判、勇于探索. 理性思維的重點是：崇尚真知，能理解和掌握基本的科學原理和方法；尊重事實和證據，有實證意識和嚴謹的求知態度；邏輯清晰，能運用科學的思維方式認識事物、解決問題、指導行為等. 質疑批判的重點是：具有問題意識；能獨立思考、獨立判斷；思維縝密，能多角度、辯證地分析問題，作出選擇和決定等. 勇于探索的重點是：具有好奇心和想象力；能不畏困難，有堅持不懈的探索精神；能大膽嘗試，積極尋求有效的問題解決方法等. 可以看到，科學精神發展的關鍵在于思維發展.

促進學生思維發展是數學教學的永恒主題.“三會”作為數學核心素養，沒有離開新中國成立以來我國數學教學目標的發展軌跡，是在繼承基礎上的發展. 智力、能力發展的核心都是思維的發展；培養思維能力的關鍵在于培養抽象與概括能力；智力、能力發展的突破口是邏輯性（深刻性）、靈活性、創造性、批判性、敏捷性等思維品質的培養. 無論數學課程再怎么改，促進學生思維發展都是數學教學永恒的主題.

4. 理解數學永遠在路上

教學中出現的問題大多數源于對數學內容的理解不到位. 教學的站位不高，思想性不強，糾纏于細枝末節，導致培養核心素養乏力，原因在于對內容所反映的數學思想和方法的理解深度不夠. 許多教師不知道該如何進行“內容解析”.

教學內容主要指《普通高中數學課程標準（2017年版2020年修訂）》（以下簡稱《標準》）的“內容標準”中所規定的數學知識及由內容所反映的數學思想方法，是實現教學目標的主要載體. 教學內容解析的目的是在準確理解內容的基礎上做到教學的準、精、簡. 這是激發學生學習興趣、減輕學生學習負擔、有效開展課堂教學、提高課堂教學質量的前提.

教學內容解析要做到：正確闡述教學內容的內涵及由內容所反映的數學思想和方法，并闡明其核心，明確教學重點；正確闡述當前教學內容的上位知識、下位知識，明確知識的來龍去脈；從知識發生發展過程角度分析內容所蘊含的思維教學資源和價值觀教育資源.

內容解析的基本結構是：教學內容的內涵；由內容所反映的數學思想和方法；當前教學內容的上、下位知識，明確知識的來龍去脈；內容的育人價值（從知識發生發展過程角度分析內容中所蘊含的思維教學資源和價值觀教育資源）.

5. 加強對學生學習方式的研究

（1）課堂互動和課堂討論的質量還有待提高.

教師缺乏對學習方式的研究，對課堂提問和課堂討論的相關理論知識了解不夠，缺乏有效組織學生自主、合作學習的方法，教師的指導能力有待提高.

（2）學習方式的變化.

調動各種感官參與數學認知過程，通過學生自己的觀察、操作、實驗，獲得抽象數學概念、原理所需要的現實材料，在此基礎上開展歸納、類比，抽象、概括活動抽取共性獲得概念，發現規律獲得原理、性質，獲得解決問題的方法的啟發.

推行體驗式學習方式，讓學生獲得數學概念、原理抽象概括的直接體驗，不僅有數學對象的要素、概念的內涵的歸納，法則、性質、公式等的歸納和發現，而且有“如何研究”“如何發現”的方法論感悟；使數學知識成為學生自己發現的結果，為理解數學知識奠定堅實的基礎，同時對應用知識的背景條件形成完整的認識；使數學學習成為學生自己可以掌控的過程. 教之道在于度，學之道在于悟.“悟”是需要時間的，教師要學會等待，不要急于“自答”.

發揮非認知因素的作用，激發學生的興趣、好奇心，調動學生的學習熱情，使學生以一種積極的態度投入探究活動中. 積極的情感體驗是激發靈感的強大動力，可以促使創造性思維的產生.

（3）教師要有正確的學生觀.

對未知事物的探索是學生的天性，需要教師倍加愛護. 教師常常因為自己對學生心理的無知，低估學生的創造力而無意間扼殺了這種天性.

學生的創新思維需要教師激發，使學生學會思考是數學教育的意義所在.

要激發學生的創新思維，教師自己應該先學會思考，歸納、類比、推廣、特殊化是基本的發現與創新之道.

以一般觀念為指導，通過問題引導思考，給學生創設獨立概括概念、性質、公式、法則的機會，這是教師的教學智慧所在.

6. 情境設計能力需要進一步提高

《標準》指出，教學情境包含生活情境、數學情境、科學情境等. 情境單一的現象比較普遍，而且存在不適當地使用生活情境和科學情境的情況. 主要問題如下.

（1）引入環節刻意聯系實際，不夠自然——幾乎所有的課都“從現實問題出發”.

（2）刻意設計探究、討論等活動環節等.

（3）情境設計不適切的情況仍然存在.

案例1：利用單位圓的性質研究正弦函數、余弦函數的性質.

環節1：生活情境引入.

師：大家有沒有坐過摩天輪？老師在暑假的時候坐過一次摩天輪. 摩天輪是一直在勻速轉動的……

環節2：發現數學問題.

師：如果把這個座艙抽象成在圓上轉動的點，把圓放在平面直角坐標系中，直接取它的半徑為1，那就是我們熟悉的單位圓，如果再將這個點定義為角x的終邊與單位圓的交點，那么角x的三角函數值與點P的坐標之間存在什么關系？

師：這就是單位圓中三角函數的定義，單位圓與三角函數有著天然的聯系，其實我們已經從單位圓中得出了三角函數的同角關系和誘導公式. 今天這節課，我們繼續通過單位圓來研究正弦函數和余弦函數的性質.

案例2：函數奇偶性的引入.

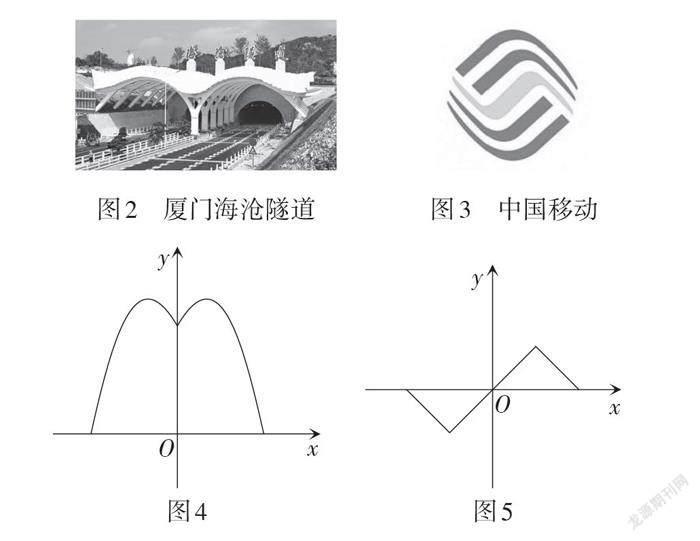
學生課前活動1：生活中，具有對稱性的圖形無處不在. 在建筑學中，簡單的結構因對稱的應用而恢宏穩定，給人一種平衡、和諧的視覺感受. 對稱是中國建筑最大的特色之一. 在品牌標志中，簡單的圖形因對稱的應用而紛繁美麗，有利于快速樹立品牌形象，打造知名度. 大家課前搜索資料，將你熟悉的具有對稱性的建筑或品牌標志的圖片上傳到問卷星鏈接中.

學生課前活動2：畫冪函數的圖象.

在課堂中，巧設情境，引入新知.

如果我們將圖2中廈門海滄隧道（世界十大跨海公路隧道）的雙連拱部分和圖3中中國移動標識的淺色部分分別抽象成曲線，并按照圖4和圖5的方式建立平面直角坐標系，就會發現這兩條曲線對應的函數的圖象分別關于y軸和原點對稱.

【設計意圖】通過具有對稱性的中國建筑物和國產品牌標志的真實情境連接教學內容和現實生活，激發學生的學習興趣，引出研究函數圖象的對稱性的必要性，即研究函數奇偶性的目的是什么.

【點評】數學教學情境應當具有豐富性，不僅僅是現實生活情境，還可以是數學情境，也可以是科學情境，要看教學內容的需要. 在數學對象的引入階段，需要創設現實生活情境、科學情境等，因為函數、幾何與代數、統計、概率等都有明確的現實生活背景或科學背景. 在數學知識發生發展過程中，要加強從數學內部提出問題的思考，多用特殊化、類比、推廣等策略. 例如，基本初等函數的性質、圖形的性質、概率的性質等一般不要用現實背景，如果用現實背景，反而會破壞數學研究的內在邏輯，不能很好地體現數學的學科特點——基于概念的推理.

上面兩個案例，都是在研究函數的性質. 從概念到性質應該是基本的研究路徑，直接提出“這類函數有怎樣的變化規律”即可，不需要從現實生活背景出發.

7. 提問能力需要進一步提高——在理解數學、理解學生的基礎上設計問題

案例3：同角三角函數的基本關系中的提問.

問題1：終邊相同的角的同一三角函數值有相等關系. 那么，終邊相同的角的不同三角函數值之間是否也有某種關系？為什么？

生1：終邊相同的角的三個三角函數值是由同一個點得到的，所以它們必然有關系．

【設計意圖】終邊相同的角的三個三角函數值之間如果沒有關系，則沒有研究的必要，通過問題引導學生明確探索的方向，堅定探索的信心．

問題2：終邊相同的角有無窮多個，那么，如何研究多個角的三角函數值的關系？

生2：因為終邊相同的角的三個三角函數值分別相等，所以只要用一個角代替所有終邊相同的角即可．

【設計意圖】利用誘導公式一，簡化探究內容．

問題3：如何探索？已知什么？能得到什么？

生3：已知三角函數的定義，易得[tanα=yx=sinαcosα.]

【設計意圖】引導學生利用聯系的觀點進行探索，利用運算發現基礎關系．

問題4：還有什么關系？三角函數是用點P的坐標定義的，那么坐標的含義是什么？啟發我們如何探究？

生4：坐標的含義啟發我們利用幾何意義進行探究.

【設計意圖】引導學生利用聯系的觀點，把代數問題轉化為幾何問題．

問題5：如圖6，[MP]和[OM]有什么關系？

生5：根據勾股定理，得到[MP2+OM2=1.] 所以sin2α + cos2α = 1．

【設計意圖】引導學生通過幾何直觀聯系直角三角形，從而聯系勾股定理，得到線段長的數量關系，探究三角函數的平方關系．

問題6：[x]就是[OM，y]就是[MP]嗎？

生6：不是，絕對值才是．

問題7：[MP2+OM2=1]任何時候都成立嗎？

生7：不是，要有直角三角形，也就是點P不在坐標軸上．點P在坐標軸上時，結論依然成立．

問題8：[tanα=sinαcosα]任何時候都成立嗎？

生8：不是，[tanα]要有意義，[cosα≠0，] 也就是角[α]的終邊不在y軸上，即[α≠π2+kπ k∈Z.]

【設計意圖】引導學生進行反思，思考推理的嚴謹性.

探究流程：發現問題—明確問題—簡化問題—研究關系—得出結論—結果精細化.

【點評】這個教學過程存在的不足是：問題瑣碎導致碎片化學習.

這里的教學要注意如下幾個方面：同角三角函數的基本關系式是三角函數的性質；從定義出發研究性質是數學研究的“基本之道”；單位圓是三角函數定義的“腳手架”，所以在發現問題“三個三角函數定義是基于同一個背景的，那么它們一定有內在聯系”，明確“只要探究同一個角的三個三角函數之間的關系”后，應該畫出單位圓，通過幾何直觀得出單位圓中相關線段的關系，后續的對稱性也是這樣. 特別提醒，“相同背景下的幾個事物之間一定有內在聯系”，這是指引發現的一般觀念.

8. 進一步增強課堂的開放性

我們的課堂仍然比較封閉，往前走一步，才能培養學生的創新思維：不能總是教師提出一個任務，學生去完成.

對于學生會做的事情和學生經過努力可以解決的問題，要放手讓學生自己去做. 這個道理教師都懂，但是在實際教學中做起來卻是另一回事. 要發揮一般觀念的思維引領作用，在方法乃至方法論上多加點撥，不要輕易把“窗戶紙”捅破.

案例4：斐波那契數列的教學.

活動1：如果一對兔子每月能生一對小兔子（一雄一雌），而每一對小兔子在它出生后的第三個月里，又能生一對小兔子，假定在不發生死亡的情況下，由一對初生的小兔子開始，1年后會有多少對兔子？

具體數據如表1所示.

除了遞推公式的性質外，還有什么性質？

我們來看看相鄰項之比怎么樣. 隨后，教師用信息技術計算“后項與前項之比”“前項與后項之比”，讓學生觀察規律.

【點評】這里的關鍵問題是什么？是如何想到“做比值”的？其實在指數函數的概念、等比數列等教學中都有這方面的經驗. 要發揮“代數學的根源在于代數運算”這一一般觀念的統領作用，引導學生思考“從哪些角度研究”“研究哪些問題”等.

這里的規律，靠觀察無法發現，只有靠實實在在地計算，從加、減、乘、除、乘方、開方等入手，讓學生自己動手.

9. 提高處理“預設”與“生成”關系的能力

問題提出后教師急于引導、提示，留給學生獨立思考的時間和空間不夠. 對于超出預設的學生回答或提問，教師不予理睬. 教師講得多、講得不得法的現象仍然存在. 有些教師把有思維含金量的內容都留給自己講解了.

10. 提升課堂小結的思想性和思維層次

課堂小結的基本結構：“四基” + “四能”. 也就是說，可以按照如下結構設計小結的問題.

（1）學習了哪些知識？是按照怎樣的過程學習的？

（2）掌握了哪些技能？具體步驟是怎樣的？

（3）領悟到了哪些思想方法？是在解決什么問題中領悟到的？

（4）學習中，對今后有啟發借鑒意義的學習經驗有哪些？

要注意，知識的回顧應該包含過程，而不僅僅是知識點的羅列.

師：今天我們學習了哪些數學思想方法呀？

生：我們學了數形結合思想、分類討論思想……

脫離內容的數學思想方法是沒有力量的.“今天我們發展了如下核心素養”之類的總結更是非常離譜！

小結中應該有反思性問題、批判性問題.（我們是如何發現……的？這個方法是如何想到的？你認為研究直線與平面垂直的性質就是要研究什么？你覺得還可以研究哪些問題？……）

小結是課堂教學的一部分，完整的學習過程非常重要.

沒有反思、總結、歸納、概括的學習會導致“入寶山卻空手而返”，這是教學效率低下的根源之一.

11. 加強過程性評價和形成性評價研究

課堂教學中的評價反饋比較薄弱，主要表現在如下方面.

（1）有的教師在課堂上對學生回答問題的反饋指導性和針對性不強，沒能及時指出學生回答中存在的問題，或對學生課堂上的生成不能合理回應.

（2）過程性評價的語言比較貧乏，大量出現“你真棒，掌聲鼓勵”.

（3）作業布置還比較傳統，作業的內容和形式都有局限性，離“提高作業設計質量，精心設計基礎性作業，適當增加探究性、實踐性、綜合性作業”的要求還有距離.

案例5：直線與方程單元復習課.

師：我們用斜率來刻畫直線的方向，結合給定的點，得到了點斜式；通過給定的兩個點，我們得到了兩點式. 除此之外，還有哪些方程的形式呢？

生1：還有斜截式和一般式.

師：有人說“直線的其他形式都是點斜式的推論”，你同意嗎？

生2：我不同意. 因為這幾個方程的適用范圍不同.

師：如果說這幾個方程在各自的范圍內，你認為這幾個方程能否用點斜式推導呢？

生2：由直線的點斜式方程推導直線的斜截式方程，就是讓一個點取在[y]軸上. 其他形式的直線方程也都可以通過這種轉換方式得到. 所以可以由直線的點斜式方程推導得到其他形式的直線方程.

師：剛才生2談到，由直線的點斜式方程經過特殊化處理可以得到直線的斜截式方程. 那么，將直線的兩點式方程特殊化為直線與兩個坐標軸的交點，我們就得到了直線的截距式方程. 事實上，直線上的兩點確定也就相當于確定了這條直線的方向，所以直線的兩點式方程也可以由直線的點斜式方程推導出來. 而我們知道，這幾種形式的直線方程都可以化為一般式. 這樣看來，這種說法確實有一定的道理.

【點評】在這段對話中，教師幫助學生解決了“直線的其他方程形式都是直線的點斜式方程的推論”的認識問題. 所以，在最后，教師不應該自己說“這樣看來，這種說法確實有一定的道理”，而應該用問題“你現在還不同意嗎？”問一問學生，讓學生自己說出“這是有道理的”.

案例6：余弦函數的對稱軸.

生1：我們通過探究得到，余弦函數的對稱軸不是只有x = 0 一條. 當[k∈N]時，x = 2kπ，x = 2kπ + π也是余弦函數的對稱軸. 綜合一下，[x=kπ k∈N]都是余弦函數的對稱軸.

師：非常好！生1稍微有點口誤，應該是角的終邊逆時針轉動一周角時，角增加2π. 他發現在單位圓中不僅可以得到余弦函數的奇偶性，而且還可以推廣到余弦函數的所有對稱軸都可以從單位圓中得到……

【點評】教師在這里應該回應什么？

要從本質上引導學生思考，從而提高學生對周期函數的認識水平. 余弦函數的對稱軸是[x=kπ k∈N，]有無數條，具有循環往復的特征，體現了余弦函數的周期性.

12. 要防止的一些現象

（1）總是全班齊答問題.

（2）讓學生各自證明，教師又采取自己的方式完成講解.

（3）較多錄像課上學生沒有帶教材.

（4）幾何內容的教學設計一張圖都沒有.

……