再生冷卻推力室準二維傳熱數值計算

吳有亮,丁煜朔,劉 瀟,劉陽旻,田 原

(北京航天動力研究所,北京 100076)

0 引言

液體火箭發動機燃燒室內充滿著高溫、高壓以及高速流動的燃氣,燃氣將對壁面產生巨大的對流和輻射熱流,若不采取有效的冷卻措施,壁溫將高到現有工程材料無法承受的程度,進而產生災難性的后果[1-2]。因此,火箭發動機傳熱和熱防護是發動機設計中的一個突出問題。現代液體火箭發動機中,再生冷卻是應用最為廣泛的冷卻技術。

再生冷卻傳熱過程涉及燃燒、流動和換熱等過程之間的耦合相互作用,導致傳熱計算相當復雜。許多學者利用商用CFD軟件對推力室傳熱過程進行三維仿真計算[3-7]。吳峰等應用經驗公式計算燃氣側對流、輻射換熱,采用氣—固耦合算法進行冷卻通道—冷卻劑三維耦合傳熱計算[8]。康玉東等考慮冷卻劑溫度分層,應用經驗公式計算燃氣側對流、輻射換熱,采用氣—固耦合算法進行冷卻通道—冷卻劑三維耦合傳熱計算[9]。Pizzarelli對高深寬比再生冷卻通道進行了三維流固耦合傳熱數值仿真,得到了較為精確的計算結果[10]。Divalentin則利用Fluent研究了通道曲率變化引起的二次流對傳熱過程的影響[11]。CFD計算雖然能夠獲得更為精確的計算結果,但是計算過程復雜,收斂性差,耗時長且對計算機配置要求高,不利于推力室冷卻結構的快速優化設計。

目前工程上傳熱和冷卻劑流阻計算主要利用一維的傳熱計算模型[12-14],將傳熱過程簡化為燃氣與內壁面之間的對流和輻射換熱、通過推力室內壁的熱傳導以及再生冷卻劑與推力室壁之間的對流換熱3個過程。一維傳熱計算模型相對實際傳熱過程做了大量簡化,忽略了冷卻通道內非對稱加熱導致的熱分層現象,隨著冷卻通道深寬比的增大,徑向溫度分層愈發明顯,遠離燃氣側壁面的冷卻劑保持著較低溫度,仍可有效地吸收熱量。采用一維傳熱模型,無法準確描述遠端冷卻劑的冷卻能力,導致計算結果與試驗測量結果存在較大誤差。燃氣側對流換熱采用經典的Bartz公式,未考慮近壁面邊界層內的導熱過程。

為了提高傳熱計算精度,本文參考文獻[15]的冷卻劑傳熱方程,建立了再生冷卻推力室的準二維傳熱數值模型,考慮了冷卻劑層間導熱導致的溫度分層效應,燃氣側增加了直接求解邊界層控制方程得到熱流密度的方法。最終基于MATLAB開發完成了通用的再生冷卻推力室準二維傳熱程序,較為準確地計算了某氫氧發動機再生冷卻推力室的傳熱情況,并與一維和三維傳熱計算結果以及熱試驗結果進行了對比,驗證了模型的準確性。

1 計算方法

再生冷卻通道的剖面結構如圖1所示,準二維傳熱模型中傳熱過程主要包括燃氣與內壁面之間的對流和輻射換熱、內壁導熱、冷卻劑沿徑向的層間導熱、冷卻劑與內壁的對流換熱。

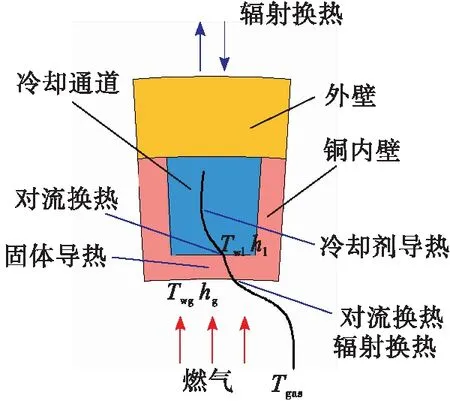
圖1 通道結構示意圖Fig.1 Channel cross-section

1.1 燃氣側傳熱

針對燃氣側對流換熱,本文研究了兩種計算方法,一種是傳統的Bartz公式,另一種是直接求解邊界層控制方程得到熱流密度。

1.1.1 傳統Bartz公式

qgc=hg(Taw-Twg)

(1)

式中:hg為燃氣側的換熱系數;Taw是燃氣絕熱壁溫;Twg是燃氣側的壁溫。

燃氣側對流換熱系數用Bartz[16]提出的管內充分發展的湍流換熱準則方程表示,即

(2)

式中:μ、cp、Pr均以總溫(Tc)ns為定性溫度;dt為燃燒室喉部直徑;d為沿燃燒室軸線計算截面的直徑;(pc)ns為燃燒室壓力;c*為特征速度;rwt為喉部處噴管外形曲率半徑。

通過附面層時氣體性質變化的修正系數為

(3)

式中:Ma為計算截面的馬赫數;k為燃氣比熱比。

1.1.2 直接求解邊界層控制方程

連續方程為

(4)

動量方程為

(5)

能量方程為

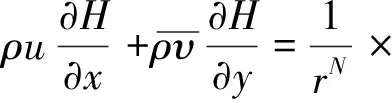
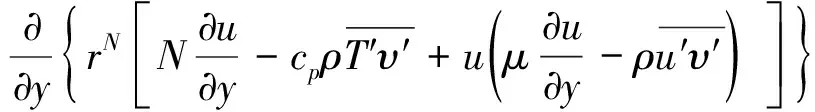
(6)

式中:ρ為密度;u為流向速度;v為縱向速度;r為橫曲率半徑;H為總焓;T為溫度;p為壓力;μ為動力黏度;cp為定壓比熱容;上標“—”為雷諾平均;上標“′”為湍流波動量;N為流動指標數,N=0時是二維流動,N=1時是軸對稱流動。

針對上述邊界層控制方程進行柱坐標轉換后,使用有限差分方法求解,并完成TDK(二維化學反應噴管流場)程序開發。具體求解過程可參考文獻[17-18]。利用自編TDK程序求解燃氣側邊界層控制方程后,直接求解不同恒壁溫條件下的熱流密度沿軸向位置分布,得到了一個燃氣側熱流密度插值表。在傳熱計算模塊中,這張熱流密度表作為輸入,通過對壁溫和軸向位置插值計算不同位置和不同壁溫下的熱流。

1.2 冷卻劑側傳熱

冷卻劑側考慮傳熱和摩擦的影響,基于質量、動量和能量的穩態守恒定律,建立了冷卻通道內冷卻劑流動模型。其中質量和動量方程以一維形式描述,而由于非對稱加熱的冷卻通道中,在徑向會產生顯著的溫度分層現象,因此流體能量方程以軸向和徑向二維形式描述。由于冷卻通道內的傳熱模型一維和二維形式并存,因此本模型稱為準二維傳熱模型。

由于動量方程為一維形式,因此冷卻劑壓力沿徑向相同,而能量方程為二維形式,所以溫度、流速沿軸向(x方向)、徑向(y方向)不同。冷卻劑物性參數如密度、焓值、黏性等沿軸向、徑向不同。

p=p(x),T=T(x,y),u=u(x,y)

其中速度可表示為

u(x,y)=umh(x)F(y)

(7)

式中:umh(x)表示通道中間位置速度沿軸向分布;F(y)表示速度剖面的形狀。

根據一維質量守恒定律

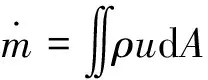
(8)

可得到中間位置速度

(9)

式中h和b分別為冷卻通道的高度和寬度。

速度剖面可表示為

(10)

式中:B為速度的不對稱率;n為與雷諾數有關的修正系數。冷卻通道內熱流傳遞過程如圖2所示。

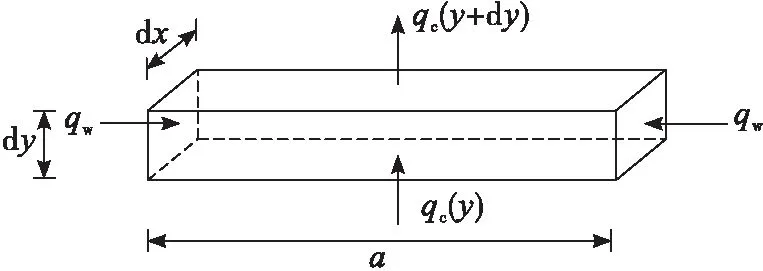
圖2 通道內熱流傳遞示意圖Fig.2 Heat fluxes in a slice of cooling channel

二維能量方程為

(11)

式中:ρ為冷卻劑密度;H0為冷卻劑總焓;qc(y)為冷卻劑層間導熱;qw為側面肋與冷卻劑的對流換熱。

冷卻劑層間熱流為

(12)

式中kt為沿徑向湍流導熱系數,與冷卻劑雷諾數Re和導熱系數λ有關,這是文獻[19]在光壁條件下提出的,kt=λ0.008Re0.9。

側面肋與冷卻劑的對流換熱熱流密度為

qw=hl(Twl-Tl)

(13)

式中:hl為冷卻劑側的對流換熱系數;qw為冷卻劑從壁面吸收的熱流密度;Twl為液壁溫;Tl為冷卻劑溫度。

對于液氫,其對流換熱系數可根據Hess-Kunz公式表示為[20]

(14)

式中:Nu為努塞爾數;Re為雷諾數;Pr為普朗特數;ν為運動黏度。

冷卻劑壓力根據一維動量方程可知

pn=pn-1-Δpn-1,f-Δpn-1,m

(15)

式中:pn為計算截面冷卻劑壓力;pn-1為前一計算截面冷卻劑壓力;Δpn-1,f為黏性壓力損失;Δpn-1,m為動量損失。

冷卻劑狀態方程為

ρ=ρ(p,T),H=H(p,T),k=k(p,T)

(16)

1.3 內壁導熱

由于冷卻通道內考慮了冷卻劑溫度分層,因此側面肋上需要考慮徑向的壁面溫度分布。燃氣側熱流通過內壁到達冷卻劑和肋,進入側肋的熱流等于側肋傳向冷卻劑的熱流,其熱流可根據穩態傳熱平衡方程表示為

(17)

式中:kw為內壁導熱系數;tw為側肋寬度。

進入側肋的熱流等于燃氣側對流換熱熱流密度,可表示為

(18)

式中δw為內壁厚度。

外壁視為絕熱壁面,因此側肋頂端導熱為0,即

(19)

1.4 輻射換熱

最大輻射熱流可表示為

(20)

式中:qr為輻射熱流密度;Tg為燃氣靜溫;εw,ef為壁面有效黑度;σ為斯忒藩—波爾茲曼常數;εg為燃氣黑度;αw為壁面吸收率;c為邊區混合比修正系數,有邊區混合比時取值0.65。

輻射熱流沿推力室軸線變化,根據最大熱流插值近似計算得到。

1.5 計算過程

根據上述的傳熱計算模型,使用MATLAB編寫了再生冷卻準二維方程程序,具體迭代求解過程如下:

1)將冷卻通道沿軸向劃分為N個截面,沿徑向劃分為M層,沿軸向依次計算每個截面上的參數分布,計算時物性參數直接調用Nist;

2)根據初始值或前一截面計算結果,給定當前截面的中間位置速度umh、冷卻劑壓力p和燃氣側內壁溫度Twg;

3)主要根據能量方程(11)、側肋導熱方程(17)、狀態方程(16)以及相關方程,由已知的umh、p、Twg,可求出冷卻劑溫度Tl、壁面溫度Tw;

4)根據質量守恒方程(8)、冷卻劑壓力方程(15)、內壁導熱方程(18),由上一步求出的Tl和Tw,可求出新的umh、p、Twg;

5)重復進行第3)、4)步的過程,迭代計算直到umh、p、Twg滿足收斂要求,即前后兩次計算差值小于0.001。

2 計算結果

2.1 計算模型

利用此程序計算了某型號氫氧發動機再生冷卻通道內的傳熱情況,并與一維傳熱計算結果和Fluent三維傳熱計算結果進行了對比。冷卻劑參數與推力室主要工作參數見表1,采用逆流冷卻方式。

表1 推力室主要工作參數

三維計算中考慮到推力室的結構對稱性,周向選擇60°作為計算區域,網格劃分如圖3所示。冷卻通道壁面粗糙度給定6.3 μm。計算過程為了提高收斂速度,采用燃氣區域和再生冷卻通道分區計算、互給邊界條件的迭代方法。求解過程中,給定燃氣壁面溫度,求解燃氣區控制方程直至收斂,得出燃氣向壁面的熱流密度,以此熱流密度為邊界條件,求解冷卻劑與冷卻通道的耦合流動換熱控制方程直至收斂,得出氣壁面溫度。如此循環幾次,如果前后兩次氣壁面熱流密度和溫度相差滿足一定的精度,則認為計算收斂。為了使收斂加速,可以先用一維經驗公式得出氣壁面熱流密度和溫度的初步分布。

湍流模型采用標準k-ε模型,應用標準壁面函數法處理壁面物理量與近壁面區域物理量之間的相互聯系,無量綱距離y+=30～300。冷卻劑熱物理性質和輸運性質隨壓力和溫度的不同而發生變化,采用自定義函數編寫。

圖3 網格模型Fig.3 Computational grids of CFD models

2.2 結果對比

圖4為燃氣側壁面熱流沿程分布,圖中CFD_3D和1D分別為三維CFD和一維傳熱程序計算結果,TDK_2D和Bartz_2D均為準二維傳熱程序計算結果,只是燃氣側熱流密度分別采用TDK程序和Bartz公式計算。不同計算方法中,一維傳熱得到的最大熱流最小,準二維Bartz公式算得熱流次之,二者得到的熱流密度曲線變化趨勢基本一致,在冷卻通道的突擴突縮處,壁面熱流有小幅度的波動。TDK程序和三維計算得到的最大熱流較為接近,圓柱段以后二者曲線吻合得非常好。但是在靠近噴注面區域,三維計算得到的熱流呈不斷增大趨勢,而TDK算得熱流反而呈減小趨勢。主要是因為三維計算考慮了燃燒過程,在噴注面附近為霧化混合區,燃燒未充分進行,熱流密度較小。此外,喉部以后區域,一維和準二維Bartz公式算得的熱流比三維和TDK程序計算結果大,可能是因為喉部以后區域內沿軸向馬赫數不斷增大,邊界層逐漸增厚,冷卻劑與內壁面之間的換熱熱阻增大,影響了傳熱過程,而Bartz公式未考慮附面層效應。

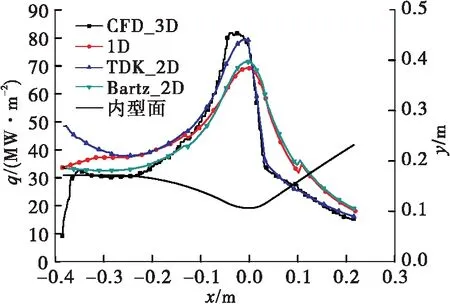
圖4 熱流沿軸向分布Fig.4 Variations of wall heat flux

造成熱流密度差異的主要原因是三維CFD與TDK程序考慮了湍流和附面層的影響,能夠較為精確地計算壁面溫度梯度,并且在計算燃氣物性中對壁面熱流計算影響較大的密度和黏度時,CFD與TDK程序均使用了物理上較為精確的公式,而巴茲公式直接使用以經驗公式表征的燃氣密度與黏度。NASA也曾使用TDK耦合RTE進行推力室傳熱計算,其熱流計算結果也與推力室CFD仿真結果吻合較好,且計算時間大大減少[21]。NASA的計算方法與國內使用的一維熱平衡傳熱程序并無本質區別,主要區別在于燃氣側熱流密度使用附面層程序求解而非巴茲公式。因此從原理上看,基于邊界層控制方程直接求解燃氣側熱流密度,對于提高工程上推力室燃氣側傳熱計算精度和效率是非常重要的。

圖5為冷卻通道中冷卻劑平均溫度沿程分布。在不同計算方法中,冷卻劑入口溫度均為35 K,在流動過程中平均溫度不斷增大。由于冷卻劑溫升主要受燃氣側總熱流影響,在喉部以后區域,采用Bartz公式的一維和準二維程序算得冷卻劑溫度偏高。在喉部以前區域,由于熱流相對較小,冷卻劑溫度增長放慢,但總的溫升與TDK_2D較為接近,具體溫升見表2。

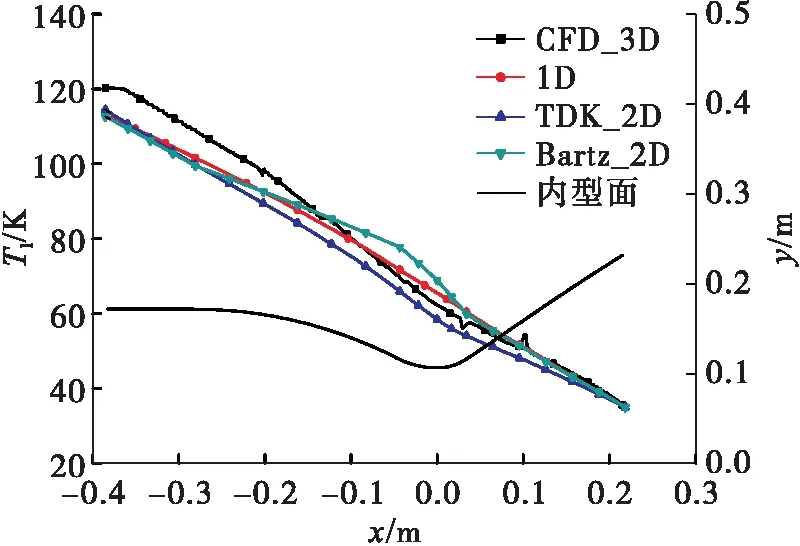
圖5 冷卻劑溫度沿軸向分布Fig.5 Variations of coolant temperature

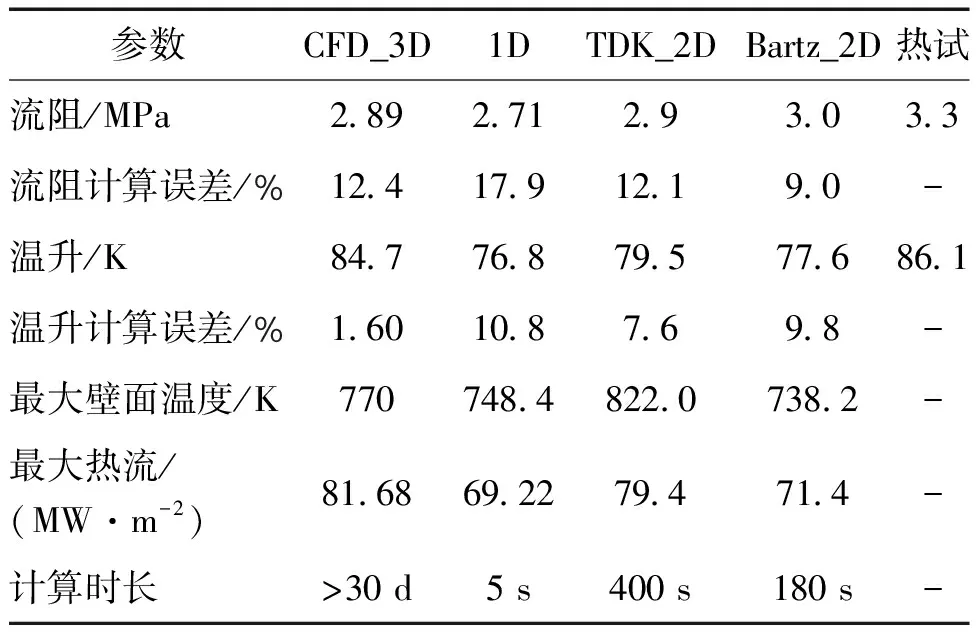
表2 不同方法計算結果

圖6為采用準二維傳熱程序計算的冷卻劑溫度分層情況,計算過程中冷卻通道內沿徑向劃分了18層單元,第1層靠近內壁,第18層靠近外壁。

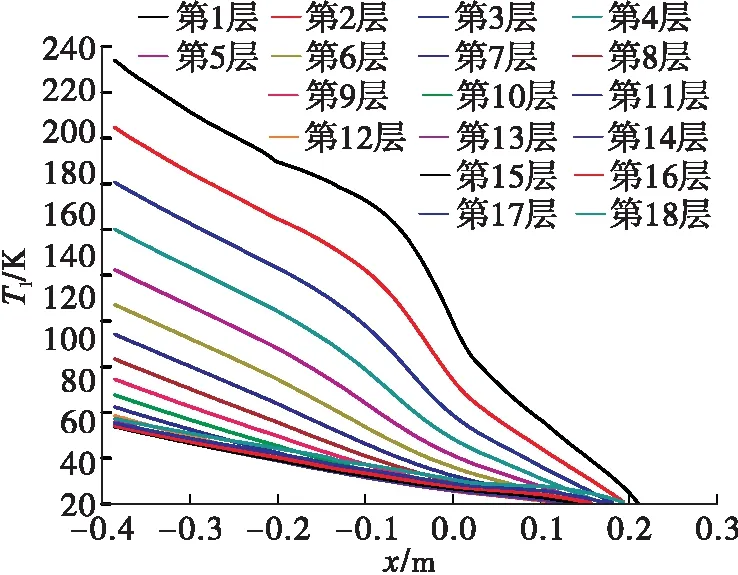
圖6 冷卻劑分層溫度沿軸向分布Fig.6 Streamwise variations of coolant temperature between different layers

可以看到冷卻劑在徑向上存在明顯的溫度分層現象,靠近內壁的冷卻劑溫度最大,出口處可達233 K,靠近外壁的冷卻劑溫度最小,出口處為76 K。因此冷卻劑的熱力學性質在同一通道截面上也存在較大差異,本文在計算過程中直接調用Nist求解每層冷卻劑的熱力學性質,避免了不均勻物性場對換熱的影響。

圖7為三維CFD和TDK_2D計算的出口截面冷卻劑溫度分布云圖,三維計算的溫度分層更為明顯,最大溫度可達350 K。

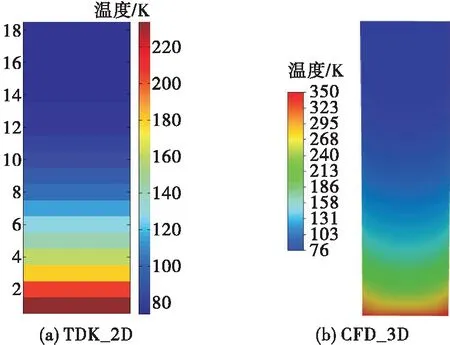
圖7 冷卻劑出口溫度分布Fig.7 Distribution of outlet temperature of coolant

圖8為冷卻劑平均壓力沿軸向分布情況,各種方法計算得到的流阻在表2中給出。在經過突擴突縮處,冷卻劑的總壓發生不同程度的損失。因為通道的橫截面積突然發生變化,冷卻劑的流速大小發生急劇改變,造成了較大的局部損失,冷卻劑的總壓下降。

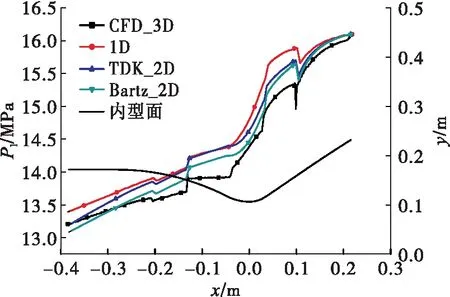
圖8 冷卻劑壓力沿軸向分布Fig.8 Variations of coolant pressure

圖9為CFD算得壁面溫度分布云圖,圖10為燃氣側壁面溫度沿程分布。各種方法計算得到最大氣壁溫在表2中給出,最大溫度分別在-0.03、0、-0.07、-0.07 m處出現。由圖中可以看出,TDK_2D和三維計算得到的壁溫曲線在喉部以后較為接近,喉部以前TDK_2D計算壁溫偏高。一維和Bartz_2D計算壁溫曲線總體趨勢較為一致,但是由于圓柱段以后溫度分層影響更為顯著,此時壁溫比未考慮溫度分層時高50 K左右。

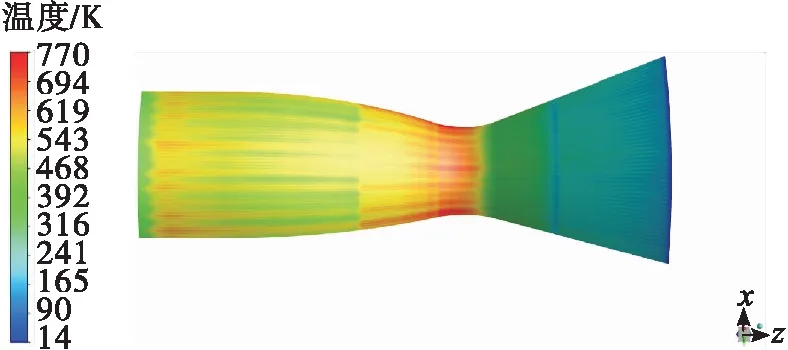
圖9 氣壁溫三維仿真結果Fig.9 Distribution of gas wall temperature for CFD_3D

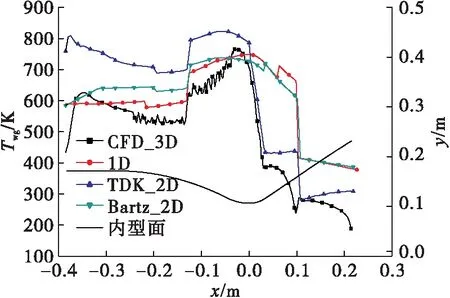
圖10 氣壁溫不同方法計算結果Fig.10 Variations of gas wall temperature

將計算得到的一些關鍵參數進行了對比,見表2。 4種方法計算的壓降均較試驗值偏小,主要是因為計算未考慮入口和出口處局部流阻損失。采用準二維傳熱程序計算的溫升與試驗值吻合得非常好,誤差在10%以內,優于一維傳熱結果。CFD算得熱流峰值最大,TDK_2D算得氣壁溫峰值最大,由于缺乏試驗值比較,計算誤差無法進行判斷。本程序雖然計算時長相對一維計算偏大,但是遠小于三維計算時間,且不用考慮前處理過程,計算方便。

3 結論

本文相對于一維傳熱模型,建立了更符合實際過程的傳熱模型,并根據理論模型建立了通用的再生冷卻推力室傳熱程序。利用該程序對某型號發動機進行了傳熱計算,通過與一維和三維傳熱計算結果的對比,可得出以下結論。

1)燃氣側采用TDK程序求解熱流密度與三維計算結果吻合非常好,而Bartz公式算得最大熱流密度偏小,在喉部以后區域內算得熱流密度偏大,喉部以前區域內偏小,綜合互補后使得計算溫升差異不大。但對于再生冷卻噴管傳熱而言,需考慮Bartz公式計算喉部以后熱流密度偏小的問題。

2)采用準二維傳熱計算方法可以計算出冷卻通道內溫度分層情況,從而考慮冷卻劑熱力學性質在同一通道截面上的差異,但沒有三維溫度分層那么明顯。

3)采用準二維傳熱程序計算的溫升與試驗值吻合得比較好,誤差在10%以內,優于一維傳熱結果;流阻計算在不考慮局部流阻損失情況下,誤差也在10%左右,滿足工程計算的要求。

4)使用準二維傳熱程序計算時間遠小于三維計算時間,且不用考慮前處理過程,計算簡單方便,效率高。