基于準一維模型的低溫流體預冷充填管路仿真分析
任孝文,周晨初,陳宏玉,李 平,劉亞洲
(1.西安航天動力研究所 液體火箭發動機技術國家重點實驗室,陜西 西安 710100;2.航天推進技術研究院,陜西 西安 710100)
0 引言
在液氧/煤油發動機、液氧/液氫發動機以及液氧/甲烷發動機[1-4]等新一代運載火箭主動力中,均存在低溫推進劑預冷充填的復雜相變過程。例如,在發射前的地面加注階段需要對主/副閥前管路進行預冷,在起動階段則需要對閥后管路及噴注器進行預冷充填。在這些過程中,低溫推進劑吸收管壁的熱量產生蒸汽,當蒸汽排出的速率小于蒸汽產生的速率時,蒸汽受到壓縮會在管內產生瞬時的壓力升高,同時液體與蒸汽的相互作用會在管路內形成一定的壓力波動;隨著管壁溫度的逐漸降低,管內蒸發量減小,流動由氣液兩相流動逐漸轉化為純液相流動。
對于使用低溫推進劑的上面級高空發動機而言,貯箱隔離閥至主閥前管路無法如一級/助推級發動機在地面進行預冷,需要在高空開展這一過程,較為準確地預測預冷時間以及推進劑消耗量,能夠顯著提高推進劑的利用率,最大限度提升有效載荷。同時掌握低溫推進劑對閥后管路及容腔的預冷充填瞬態特性[5],能夠為燃燒組件點火時序的制定提供重要參考。
目前國內外現有的管路預冷模型大多忽略充填的動態過程而將關注點集中于預冷消耗量和預冷時間方面。典型的研究工作有:李永兵等進行的輸送系統循環預冷數值仿真,其通過一維兩流體模型詳細研究了各種參數對預冷效果的影響[6];王嬌嬌等采用準穩態方法建立了一維預冷計算模型,其采用一維均相法,考慮了輻射漏熱的影響,結果表明存在一個最優質量流速使得預冷時間縮短的同時減少推進劑的浪費[7];Darr等假設流動速度恒定,進行了液氮預冷管路的一維計算[8]。
在考慮充填等瞬態流動的預冷過程方面,程謀森等針對氫/氧液體推進劑供應管路的充填過程進行了研究,其采用一維均相模型以統一的方程描述亞臨界和超臨界態的流體流動,使用特征線差分方法進行數值求解,計算結果近似反映了充填過程的動態特性[9];同樣針對氫氧發動機供應管路,劉昆等使用有限元分割的方法采用一維均相模型進行了仿真計算,其中兩相單元使用了等效流容方程[10]。此外,美國GFSSP[11]、歐洲ESPSS[12]、德國THESEUS[13]等程序在處理兩相流動時均使用了一維均相模型,該模型在每個控制體內假設所有相態的壓力、溫度及速度是均勻平衡的,忽略氣液相間的滑移速度。
在兩流體模型方面,由于其極大的復雜度,至今未有成熟的、完整的兩流體模型應用于充填過程的系統級仿真中。近年來,針對歐洲新一代低成本可重復使用液氧甲烷發動機的動態仿真要求[14-15],馮卡門研究中心(Von Karman Institute)在與羅馬大學和西班牙EAI公司(Empresarios Agrupados Internacional)的緊密合作下基于ESPSS仿真模型庫在兩相流動領域進行了持續大量的投入,其研究表明得到預期穩定的非均勻兩相流模型是存在一定難度的[16],最新發布的ESPSS 3.2.4測試版本加入了兩流體六方程模型來處理兩相流動,但目前通過的測試僅限于不含相變的理想空氣與水的兩相流動問題[17],能夠處理相變情況下的兩相流動仍在持續的研發完善中。
本文在常溫推進劑充填管路的水擊和流動振蕩研究的基礎上[18-22],采用非因果建模的Modelica語言[23]基于MWorks仿真平臺建立了準一維有限體積的預冷充填模型。本文模型與公開文獻已有模型的不同之處在于,除基本控制方程外新增了充填率對流方程,并采用一維形式求解該方程及能量方程,質量方程及動量方程則使用集總參數形式。通過定義相同的接口模塊,本文建立的預冷充填管路組件模型可與液體火箭發動機瞬態特性模塊化通用仿真模型庫[24]中的其他組件模型進行數據交換,拓展了該模型庫的仿真能力。最后,為獲得低溫流體預冷充填管路的主要特性,利用本文模型分別研究了不同結構初溫及不同低溫介質對預冷充填過程的影響。
1 計算模型
1.1 數學模型
低溫流體預冷充填管路的典型流動物理過程如圖1所示,根據流型圖譜可細分為泡狀流、反環狀流、彌散流等[25]。
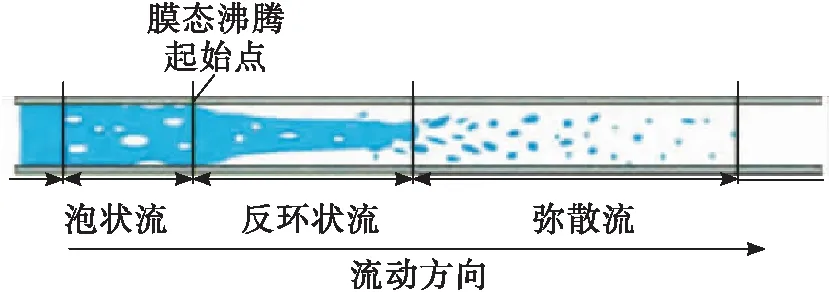
圖1 預冷充填典型物理過程Fig.1 Physical process of pre-cooling filling
為簡化模型并提升系統仿真效率,假設蒸汽與低溫流體之間具有明確的分界面且垂直于流動方向,分界面的移動速度即為液體充填的速度,且氣液之間不存在速度滑移,即氣液等速;忽略流體之間的導熱,管路橫截面沿流向為定值;流動過程使用集總參數的方法描述,換熱過程和充填率的計算采用一維分布參數的形式描述,如此得到的計算模型如圖2所示。
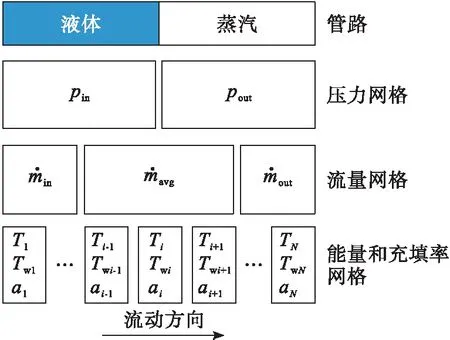
圖2 預冷充填計算模型(i為網格索引)Fig.2 Simulation model of pre-cooling filling (i is index of node)
當液體未充滿管路,即管路內總的充填率αt< 1時,根據質量守恒定律,液體部分的壓力計算式為
(1)
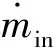
根據質量守恒定律,氣體的積存量變化由液體汽化率和氣體排出的流量決定,即
(2)
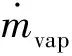
結合氣體狀態方程,氣體部分的壓力計算式為
(3)
式中:pout為管路出口壓力;L為管路總長度;R為蒸汽氣體常數;T為流體溫度。
液體部分流出流量的計算式為
(4)
式中:d為管路直徑;λ為達西摩擦系數;ρL為液體密度。
由于氣液等速的假設,氣液界面的移動速度usf計算式為
(5)
氣液界面的位置,即已充滿液體的長度l計算式為
(6)
管路總的充填率αt為
(7)
當液體充滿管路,即管路內總的充填率αt=1時,上述方程均切換為如下液體的質量與動量方程。
液體的壓力為
(8)
(9)
式中pin和pout分別為管路充滿液體后入口和出口的壓力。
液體的流量為
(10)
一維分布參數形式的能量方程為
(11)
式中:q為壁面傳給流體的熱流密度;表觀比熱容cp由飽和狀態的氣相比熱容cpg和液相比熱容cpL計算得到,即
cp=αcpL+(1-α)cpg
(12)
式中α為單個網格內的液體充填率,表觀密度ρ具有相同的形式。
一維形式的充填率對流方程為
(13)
這樣在求解過程中,隨著充填過程的進行,每個網格中的充填率α將從0到1變化,每個網格內能量方程中的密度與比熱容即會從氣相逐漸轉變為液相。
(14)
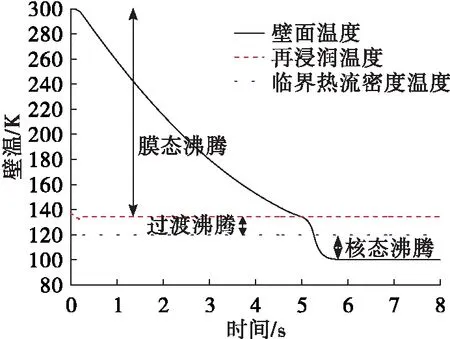
低溫流體與過熱壁面的沸騰換熱過程可根據壁面溫度Tw與再浸潤溫度TMHF、臨界熱流溫度TCHF及流體飽和溫度Tsat的大小劃分為膜態沸騰、過渡沸騰以及核態沸騰3個區域:
1)Tw>TMHF,膜態沸騰階段;
2)TCHF 3)Tsat 具體計算方法可參見文獻[7]。 不考慮管壁之間的導熱以及環境的熱泄漏,每個網格內的管壁釋熱方程為 (15) 式中:Tw為管壁溫度;mw為管壁質量;cw為管壁比熱容。 本文的數值計算基于Modelica語言的面向對象建模的MWorks仿真平臺,由于該平臺能夠使用時間步長自適應的DASSL算法[26]求解代數方程和常微分方程組,因此只需要將能量方程及充填率對流方程的空間偏導部分進行數值離散,將分布參數的偏微分方程組轉化為網格單元內的常微分方程組。 由于充填鋒面垂直于管路軸向的假設,網格內充填率只有0和1兩種狀態,因此隨著充填狀態由未充填到充滿的變化,單個網格中的充填率是一個從0至1的階躍過程。這就要求空間偏導的離散具有迎風性好、耗散性小的特點,對此,本文采用TVD格式[27]進行空間離散。 本文開發的模型將一階、二階迎風格式及7種TVD格式全部集成在了該組件模型中,并可以在用戶界面下拉菜單進行選擇,如圖3所示,大大降低了模型應用難度。 圖3 參數設置用戶界面Fig.3 User interface of parameter setting 美國弗洛里達大學Darr等在NASA馬歇爾空間飛行中心的資助下,開展了液氮預冷管路的試驗研究[8]。試驗的目的在于獲得低溫液氮充填垂直不銹鋼管路的預冷曲線,為了能夠對預冷沸騰中3種沸騰機制提供足夠多的數據支撐,試驗工況涵蓋了較為寬廣的質量流量和壓力范圍。試驗中選擇液氮作為低溫介質,不僅是出于安全性的考慮,還因為液氮的表面張力、沸點和汽化潛熱等物性與液氧較為相似。試驗中,流動方向與重力方向相同,對于所有的工況,試驗段管路的初始溫度保持在室溫293 K。 圖4所示為針對Darr試驗段搭建的仿真模型,其中預冷充填管路分為20段。 圖4 針對Darr試驗的仿真模型Fig.4 Simulation model for Darr experiment 圖5所示為6種不同工況下管路中部壁面溫度隨時間的變化曲線,其中G為質量通量,ReL為流動雷諾數,pin為入口壓力。從對比結果來看,本文仿真模型能夠較好地模擬各個工況下的預冷過程中壁面溫度的變化,而Darr等學者的模型與試驗數據有一定的差距,原因在于其模型在計算過程中假設流動過程的流量及壓力不隨時間變化,而僅僅考慮了溫度的動態變化過程;而本文模型在考慮低溫流體對管路充填這一動態過程的同時計算了流體與管路之間的熱交換。 圖5 仿真結果與試驗數據對比Fig.5 Simulation results versus experimental data 對于管路預冷過程而言,在工程實踐中通常比較關心的是預冷時間,即管壁溫度需要多長時間才會降至低溫流體的溫度。因此,應以預冷時間為指標進行仿真模型的誤差對比,誤差計算公式為 (16) 式中:tsim為預冷時間仿真值;texp為預冷時間實驗值。 表1給出了本文仿真模型與Darr等仿真模型對預冷時間的計算誤差。 表1 預冷時間仿真誤差 從表1可以看到相比于實驗數據,兩種模型的計算誤差均不超過13%,而本文模型誤差相對更小(小于6%),這表明本文模型對預冷流動過程的描述更為準確,且使用的對流換熱經驗關聯式也較為合理。 為進一步確認本文建立的管路預冷充填模型的有效性,對Jin等學者的試驗[28]進行了仿真。試驗中流體介質為低溫液氧,試驗系統如圖6所示,管路全長7 m,內徑10.2 mm,管路外包覆有厚度21 mm的絕熱層,以減少周圍環境向管路的熱泄漏,在管路外壁面如圖A、B、C位置布置有溫度傳感器。仿真模型見圖4,管路分段數為100。 圖6 Jin等試驗系統示意圖Fig.6 Diagram of experimental system of Jin et al 圖7及圖8給出了兩種工況下的實驗數據與仿真結果對比,本文仿真模型計算得到的壁面溫度變化基本與實驗趨勢一致。由于管路較長,且質量通量G較小,因此管路預冷時間較長,在實驗工況范圍內最長預冷時間達到了400多秒。且從不同管路位置的壁面溫度曲線來看,管路上游(A位置)的冷卻速度快于管路下游(B位置)的冷卻速度,管路中部(C位置)的冷卻速度介于兩者之間。 圖7 仿真結果與試驗數據對比[G=24.5 kg/(m2·s), Re=2 071, pin=557 kPa]Fig.7 Simulation results versus experimental data[G=24.5 kg/(m2·s), Re=2 071, pin=557 kPa] 圖8 仿真結果與試驗數據對比[G=41.6 kg/(m2·s), Re=4 010, pin=817 kPa]Fig.8 Simulation results versus experimental data[G=41.6 kg/(m2·s), Re=4 010, pin=817 kPa] 圖9與圖10所示為對應于兩種工況下,本文模型計算得到的管路內壓力及充填率變化曲線。由于預冷過程中,液氧吸收常溫壁面的熱量發生了汽化,因此在管路充滿前,管內處于氣液兩相狀態,管內壓力主要由汽化而來的氧氣決定,且從圖中看到隨著充填的進行,管內壓力出現了一定的波動。而在液氧充滿的瞬間,由于圖6中閥門3流阻的作用,產生了明顯的水擊壓力。 觀察圖7及圖9,在pin=557 kPa的工況下,圖9中充填率曲線表明管路內液氧在300 s左右即顯示充滿,而在圖7中,300 s時刻管路中部(C位置)仍未完全冷卻至流體溫度;在pin=817 kPa的工況下,圖10中充填率曲線表明管路內液氧在220 s左右顯示充滿,在圖8中,此時管路末端壁面溫度未冷卻至流體溫度。這一不合理之處是由于本文模型的假設造成,其假設充填過程中流動具有明確的氣液界面,且垂直于管路內流體流動方向,該氣液界面左側為純液相,右側為純氣相,如圖2所示。 圖9 管路壓力及充填率[G=24.5 kg/(m2·s), Re=2 071, pin=557 kPa]Fig.9 Pressure and filling rate of pipeline [G=24.5 kg/(m2·s), Re=2 071, pin=557 kPa] 圖10 管路壓力及充填率[G=41.6 kg/(m2·s), Re=4 010, pin=817 kPa]Fig.10 Pressure and filling rate in pipeline[G=41.6 kg/(m2·s), Re=4 010, pin=817 kPa] 該假設導致準一維管路網格內的充填率非0即1,并沒有介于0~1之間的狀態,而實際上在壁面溫度還未完全冷卻至流體溫度的情況下,流體中依然含有較少的蒸汽。即本文建立的準一維管路預冷充填模型中,充填率實際并不是嚴格的純液相的充填率,而是液體含量較大的兩相流體與純氣相之間的分界面。這也是為什么在液氧質量通量較大時,圖8中管路末端溫度降低至液體溫度的時刻與圖10中充填率達到1的時刻較為接近,分別為270 s與220 s左右;而在液氧質量通量較小時,圖7與圖9中的相應時刻分別為400 s與300 s左右。 這一點是該模型的局限性,但是與壁面溫度的實驗數據對比可知,該模型在預測管路預冷時間方面是較為準確的。同時由于該模型計算得到充填率為1時,從圖7和圖8中也可看到,膜態沸騰階段已經基本結束,大流量的低溫流體已經充填至管路末端,而燃燒組件點火時序的制定依據也是大流量推進劑的進入時刻,因此后續將該模型應用于發動機起動過程的動態仿真分析是合理的,是有一定的工程意義的。 使用圖4搭建的管路預冷系統模型,研究壁面初始溫度對預冷充填管路的影響。低溫介質為液氧,管長2 m,內徑10 mm,壁厚1.25 mm,貯箱供應壓力1.0 MPa,該參數下對應的穩態流動質量通量G=12 755 kg/(m2·s),0 s時刻閥門開啟,充填開始進行。在上述參數一定的前提下,分別計算管路初始溫度300 K、400 K、500 K、600 K時的預冷充填過程。 圖11所示為計算得到的管路不同位置的壁面溫度變化曲線,圖12所示為不同初始壁溫下管路內壓力變化曲線的對比,圖13所示為不同初始壁溫下管路內充填率的對比。從以上計算結果可以看到,隨著管路初始溫度的增高,液氧對管路的預冷時間逐漸增長:管路末端位置預冷完全的時間從管壁初始溫度300 K工況下的3 s逐漸增加至管壁初始溫度600 K情況下的6 s。 當管路初始壁溫升高時,管路內充填開始時由蒸發產生的氧氣量也逐漸增多,導致圖13中的充填時間逐漸增長,同時導致了在圖12中蒸發氣體的建壓時間縮短,氣體建壓的壓力峰值逐漸增大,管路內壓力波動也更加明顯;并且由于氣體的緩沖作用,在低含氣率的液氧充滿管路時管路末端節流元件位置的水擊壓力逐漸減小,各項具體數據見表 2。 圖12 不同初始壁溫下管路出口壓力變化Fig.12 Change of pipeline outlet pressure under different initial wall temperatures 圖13 不同初始壁溫下管路內充填率Fig.13 Filling rate under different initial wall temperatures 表2 不同初始壁溫下管路充填過程的特征數據 在3.1節液氧預冷充填管路的基礎上,更換流體介質為液甲烷和液氮進行不同低溫介質預冷充填過程的對比研究,仿真過程參數設置與3.1節相同,其中管壁初始溫度保持在300 K,且入口流體溫度均設置為100 K。 圖14給出了3種低溫流體預冷充填過程中壁面溫度的變化曲線,可以看到,在給定管路入口壓力溫度及管路流阻的情況下,液甲烷的預冷速度最快,液氮預冷速度最慢,液氧介于兩者之間。但是由于3種低溫介質的密度不同(3種介質中液甲烷密度最小,液氧密度最大),因此在入口壓力及管路流阻相同的條件下,3種流體的穩態流速是不相同的,液氧、液甲烷、液氧流速分別為11.87、18.83、13.69 m/s;而由于流體的流速對對流傳熱過程的影響較大,因此若要分析介質的不同(主要是物性參數的不同)對預冷充填過程的影響,則需要將流速的影響剔除。 圖14 預冷充填過程中管路出口位置壁面溫度變化Fig.14 Change of wall temperature at outlet of pipe 基于上述分析,針對不同介質的預冷充填過程,保持管路結構參數一定,調整管路流阻。由于充填過程為非穩態過程,充填過程的流速是隨時間變化的,而在非穩態過程中保持3種介質的流速相同是很困難的,因此此處采用調整管路流阻以保證3種低溫介質的穩態流速相同的辦法來盡可能剔除流速的影響,穩態流速均為11.87 m/s。 圖15所示為相同穩態流速下的液氧、液甲烷及液氮預冷充填管路的壁面溫度計算結果,該溫度為管路出口位置的壁面溫度。 圖15 相同流速下管路出口位置的壁面溫度Fig.15 Change of wall temperatures under same flow velocity 可以看到液氧預冷時間最短,用時3 s,液甲烷的預冷時間次之,用時4 s,其中液氧的預冷速度先慢后快,液甲烷的預冷速度先快后慢,而液氮的預冷速度最慢,所需要的預冷時間最長,為5.5 s。 為分析出現以上差別的原因,圖16~圖18分別給出了3種低溫流體充填過程的壁面溫度變化以及再浸潤溫度(temperature of minimum heat flux)與臨界熱流密度溫度(temperature of critical heat flux)對沸騰換熱區域的劃分。 圖16 液氧預冷充填管路的沸騰傳熱Fig.16 Boiling heat transfer of liquid oxygen pre-cooling filling pipe 圖17 液甲烷預冷充填管路的沸騰傳熱Fig.17 Boiling heat transfer of liquid methane pre-cooling filling pipe 圖18 液氮預冷充填管路的壁面溫度及沸騰傳熱分區Fig.18 Boiling heat transfer of liquid nitrogen pre-cooling filling pipe 可以看到,對于圖16中的液氧而言,預冷過程中膜態沸騰、過渡沸騰以及核態沸騰3種沸騰機制均較為明顯;而對于圖17中的液甲烷,預冷過程中過渡沸騰與核態沸騰占據主導,膜態沸騰對預冷過程的影響較小。由于核態沸騰階段的對流換熱系數較大,而膜態沸騰階段的對流換熱系數較小,因此在大部分時間內(液氧進入核態沸騰前),液甲烷的預冷速度快于液氧;而由于液氧與液甲烷物性的不同,在核態沸騰階段,相比于液甲烷,液氧與壁面的對流換熱系數更高,因此液氧預冷所用時間更短。 圖18中的液氮預冷過程中,在大部分時間內膜態沸騰占據主導,因此液氮的預冷速度最慢。造成上述3種低溫介質預冷換熱分區不同的原因主要在于,相同壓力下,液氮的飽和溫度最低,液甲烷的飽和溫度最高,液氧的飽和溫度介于二者之間,因此充填過程中,圖16~圖18中液氮的膜態沸騰區域占比最大,液甲烷的膜態沸騰區域占比最小,液氧的膜態沸騰區域介于兩者之間。 本文建立了準一維有限體積的預冷充填管路模型,并研究了不同結構初溫及不同低溫流體對預冷充填過程的影響,獲得的結論如下。 1)隨著管路初始溫度的增高,液氧對管路的預冷時間逐漸增長,充填開始時蒸發產生的氧氣量逐漸增多,導致蒸汽建壓時間縮短,氣體建壓的壓力峰值逐漸增大,管路內壓力波動也更加明顯;同時由于氣體的緩沖作用,在低含氣率的液氧充滿管路時管路末端節流元件位置的水擊壓力逐漸減小。 2)在相同穩態流速下,液氧預冷速度最快,液甲烷次之,液氮的預冷速度最慢。在液氧預冷管路的過程中膜態沸騰、過渡沸騰以及核態沸騰3種沸騰機制均較為明顯;在液甲烷預冷管路的過程中,過渡沸騰與核態沸騰占據主導,膜態沸騰對預冷過程的影響較小;而在液氮的預冷過程中,在大部分時間內膜態沸騰占據主導。 3)后續將在本文建立的準一維預冷模型基礎上進一步開展一維預冷模型研究,并考慮環境熱泄漏對預冷過程的影響。1.2 計算方法
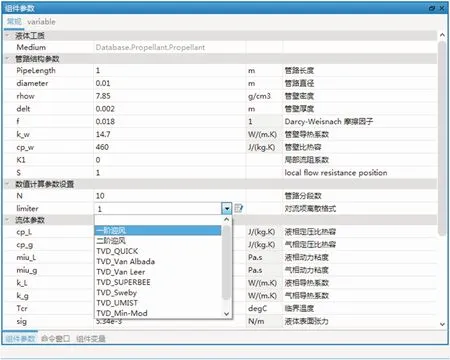
2 模型驗證
2.1 液氮預冷充填管路
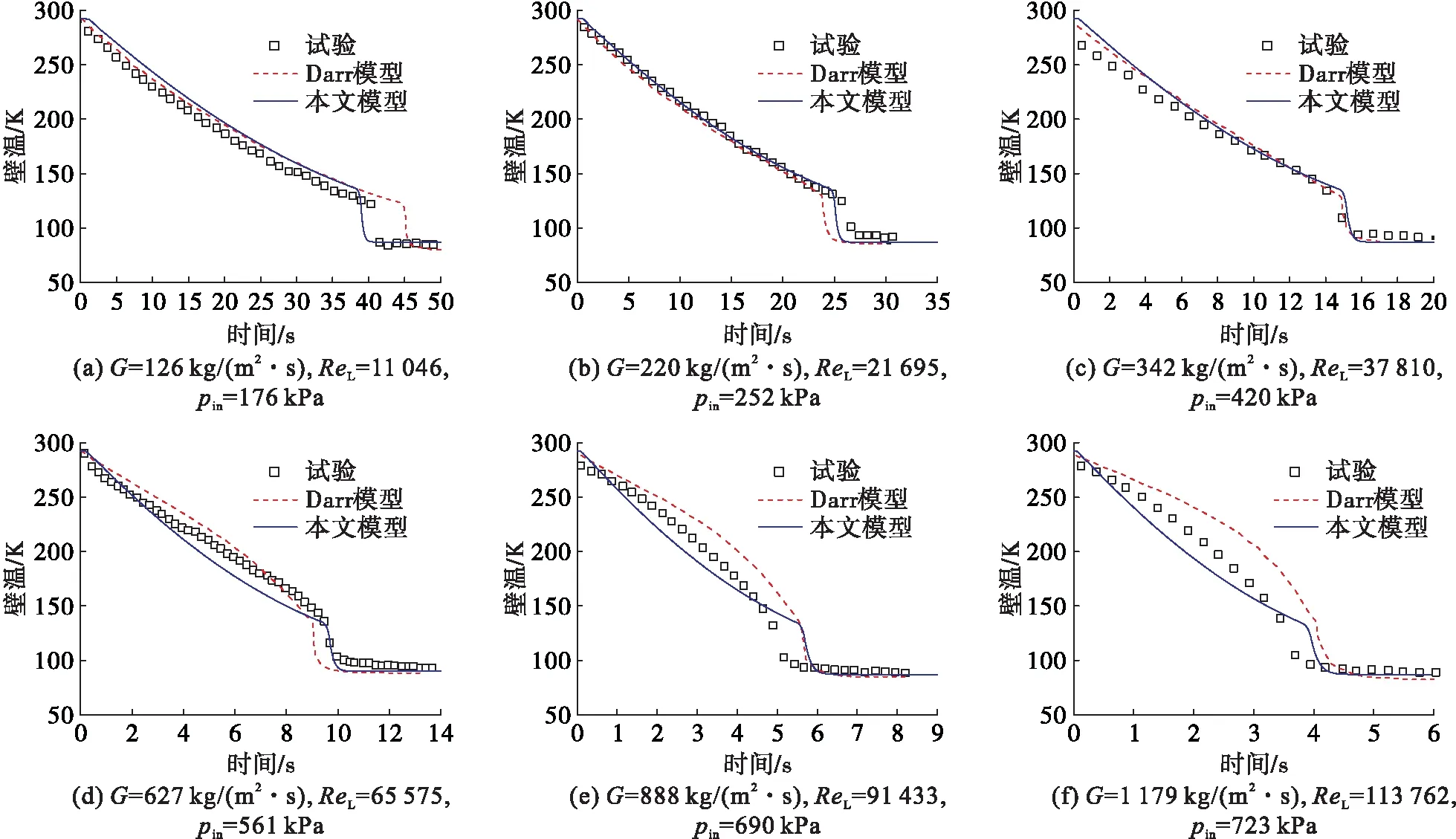
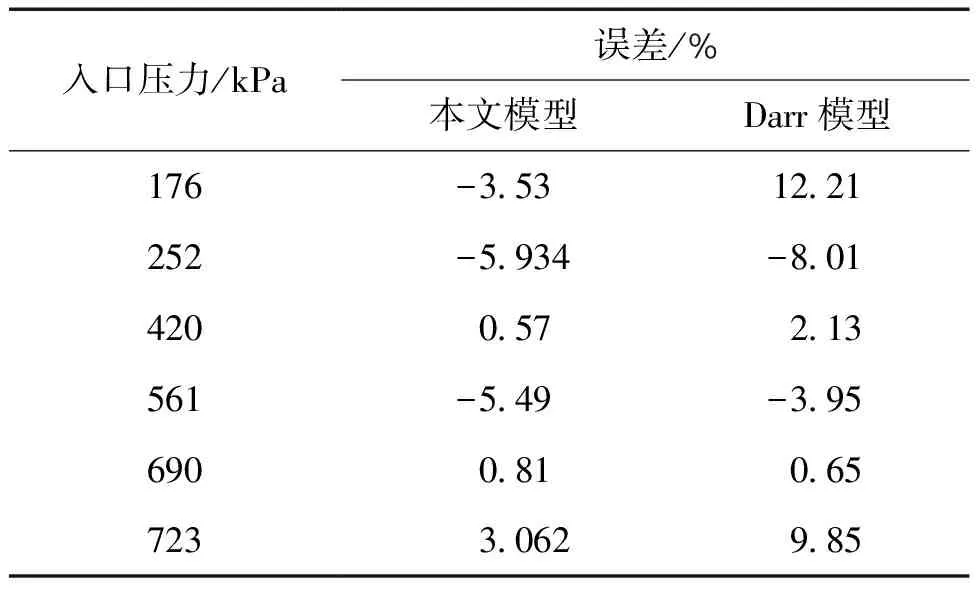
2.2 液氧預冷充填管路
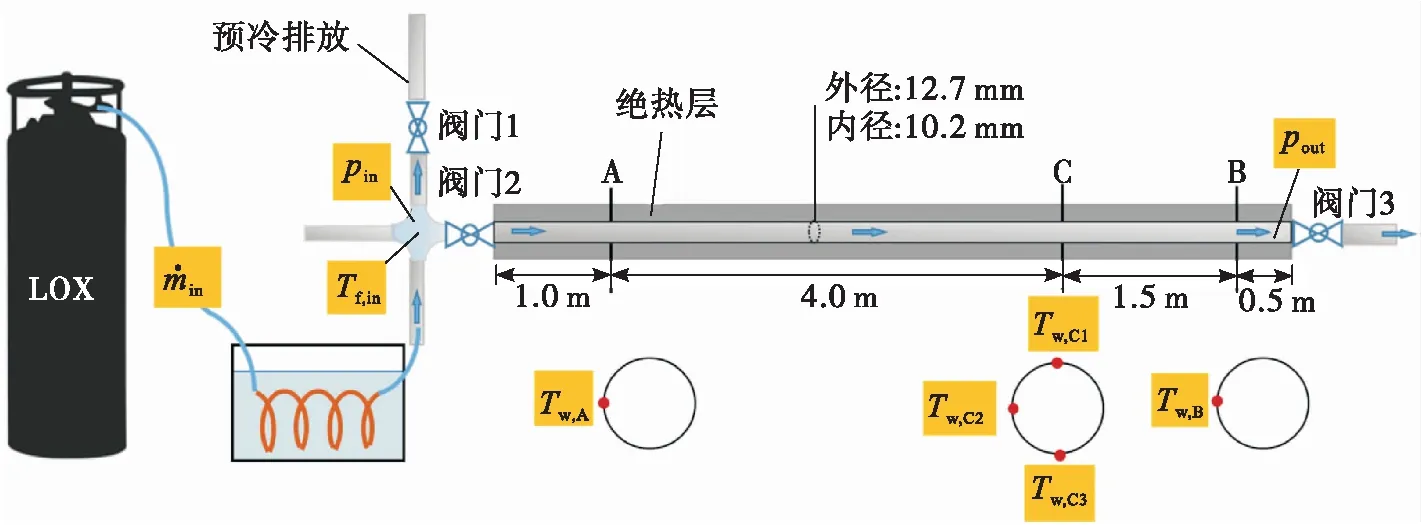
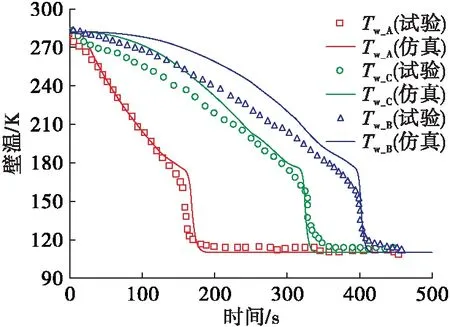
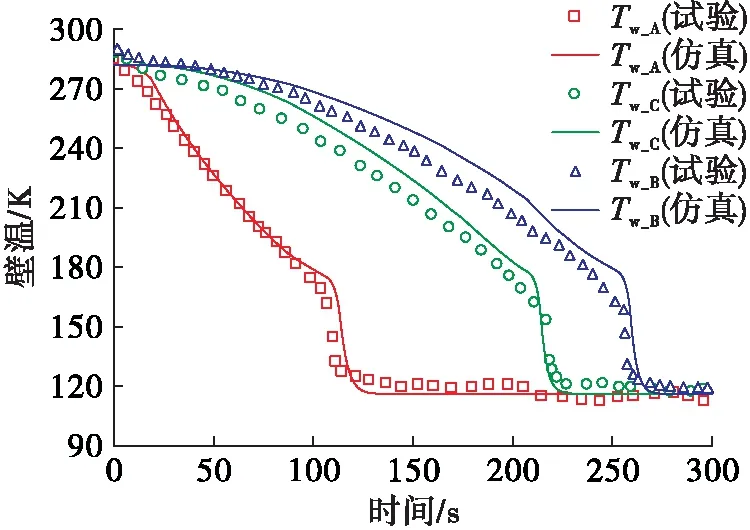
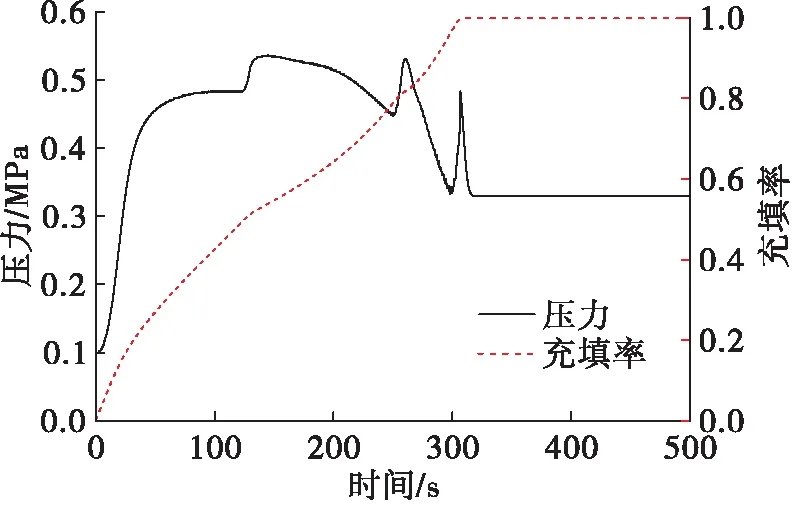
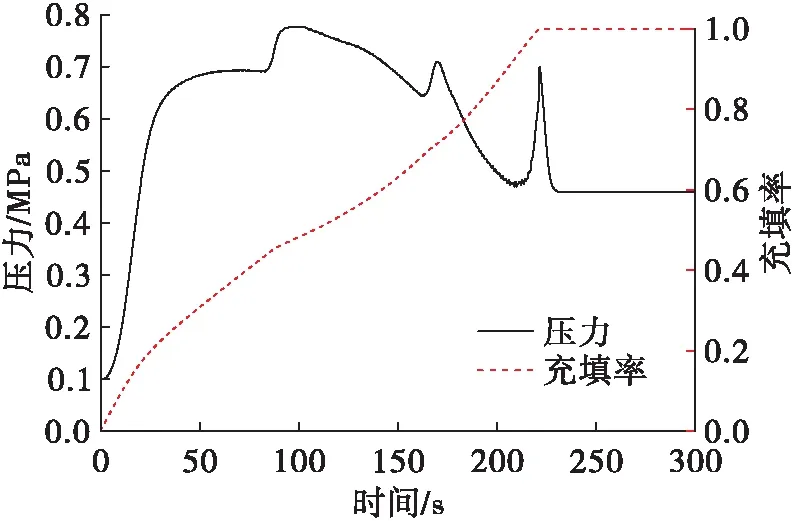
3 仿真分析
3.1 壁面初始溫度對預冷充填管路的影響
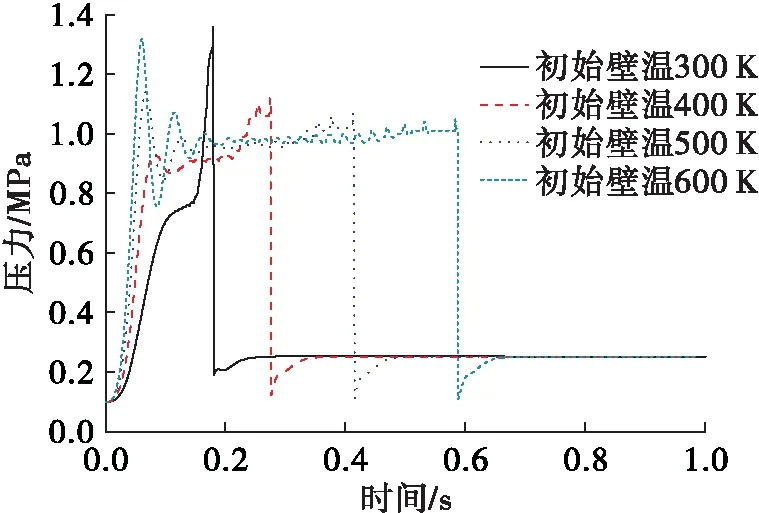
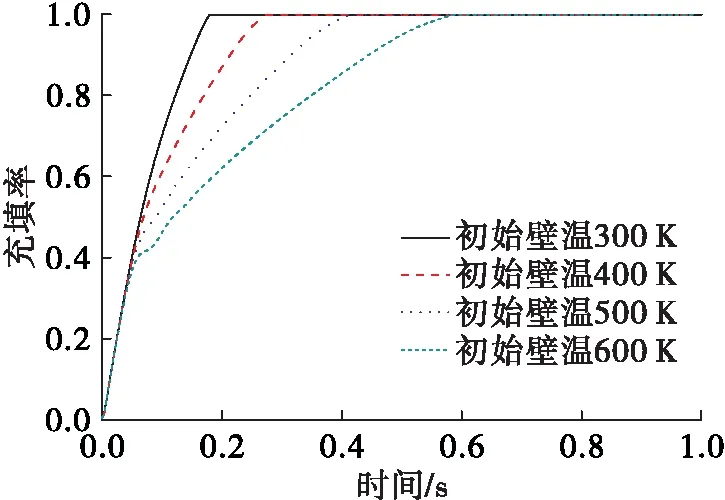
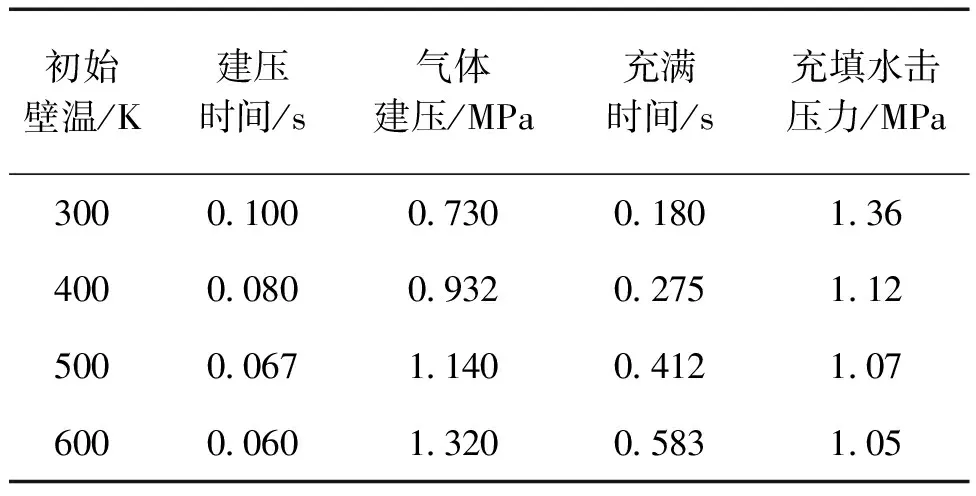
3.2 不同低溫介質對預冷充填過程的影響
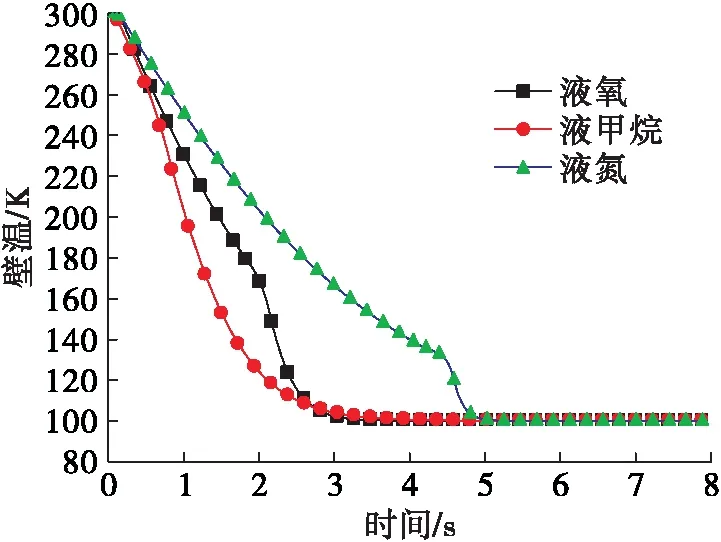
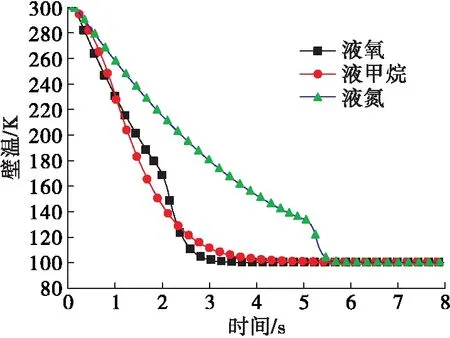
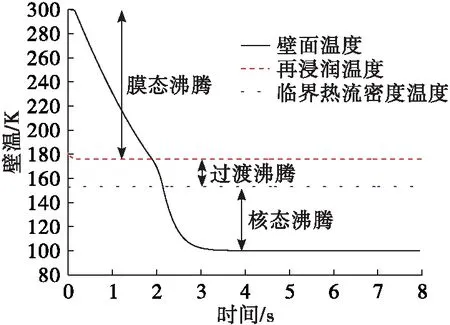
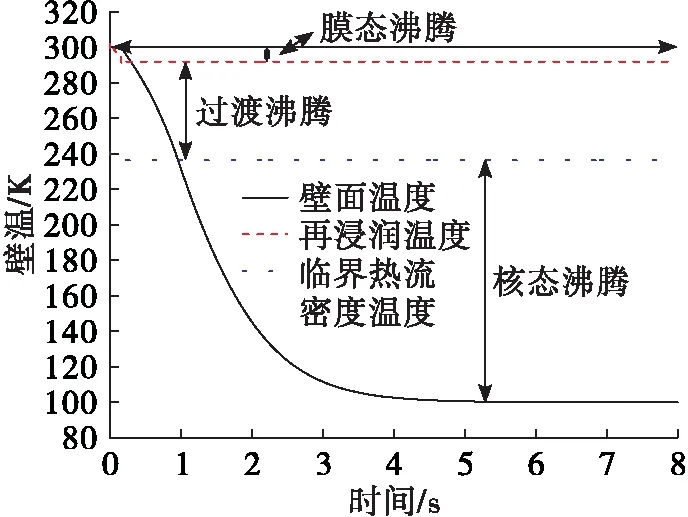
4 結論

