L形方鋼管混凝土組合異形柱弱軸抗震性能研究

康 寅,王 培

(1.青島酒店管理職業技術學院 酒店工程學院,青島 266100;2.青島理工大學 理學院,青島 266525)

近年來,異形柱結構以其獨特的優勢逐漸受到工程建設者的青睞。相較于框架結構,異形柱結構不露柱腳,不占用使用面積,建筑效果好;相較于剪力墻結構,異形柱結構柱肢短,造價低[1]。但是由于異形柱的質心與剛心不重合,導致其抗扭剛度及抗震性能均低于規則方柱[2]。我國規范[3]對異形柱結構的最大適用高度有嚴格的限制,且在8度(0.30 g)及9度區禁止使用異形柱結構,而這無疑對異形柱結構的推廣產生了一定的影響。

為提高異形柱的抗震性能,參照鋼管混凝土柱的設計思路,陳志華等[4]將多個方鋼管混凝土柱用連接鋼板相連,設計出了一種L形方鋼管混凝土組合異形柱(LCFT柱),如圖1所示。軸壓[5]及壓彎[6]承載力試驗證明:LCFT柱的破壞模式以繞弱軸的扭轉失穩為主,其承載力與普通混凝土異形柱相比有較大提升。周婷[7]對LCFT柱試件施加A向(圖1)的低周反復作用,對其強軸的抗震性能進行了研究,試驗證明:LCFT柱繞強軸方向的延性系數約為2.7,具有較好的抗震性能。鑒于上述研究基礎,陳志華等將方鋼管混凝土組合異形柱框架結構應用于汶川漁子溪村的災后重建[8],取得了良好的社會效益和建筑效果。

圖1 LCFT柱示意

綜上所述,LCFT柱抗震性能良好,可用于工程實際。但這一研判多是基于其強軸的抗震性能,相關的試驗及有限元模擬也多是從A向施加低周反復荷載。而L形截面存在弱軸且地震波的來向具有不確定性,因此本文利用ABAQUS有限元軟件從B向(圖1)對LCFT柱施加低周反復荷載,對其弱軸的抗震性能進行了研究。

1 試件設計

選用常用建筑材料C30混凝土及Q235鋼材進行試件設計。如圖2所示,參考常用民居建筑的層高,取柱高為3000 mm;為保證連接鋼板的局部穩定,參考相關規范[9],在連接鋼板的兩側對稱設置橫向加勁肋,外伸長度B取為(L′/30+40),縱向間距取為1.5L′,厚度與連接鋼板相同,均為6 mm;為節約鋼材降低造價,在連接鋼板的中部開設圓洞,直徑為0.5L′,縱向間距為1.5L′。試驗以柱肢厚度H、方鋼管壁厚t及柱肢長厚比n(n=L/H)為變量設計試件,試件編號及相關參數如表1所示。

圖2 試件示意

表1 試件構造尺寸

2 有限元參數設計及驗證

2.1 混凝土本構模型

采用塑性損傷本構模型[10],彈性模量取驗證試驗[7]的實測數據,其余參數參考相關試驗[11]的有限元設置,如表2所示。

表2 塑性損傷本構模型參數

2.1.1 混凝土受壓本構模型

鋼管中的混凝土在受壓時處于四面約束的狀態,與普通混凝土的受力狀態并不相同[12],為模擬其應力-應變特性,當應變ε≤10εc0時,選用與李威[11]相近的本構模型;當應變ε>10εc0時,為使模擬結果中骨架曲線的下降段與驗證試驗相契合,經試算,選用線性下降的本構關系,如式(1)所示。

(1)

式中:yc=σ/σc0;xc=ε/εc0;εc0=1300+12.5f′c+2ξ0.2·[1400+800(f′c/24-1)];σc0=[1+(-0.054ξ2+0.4ξ)·(24/f′c)0.45]·f′c;ξ=fyAs/fckAc;q=ξ0.745/(1+ξ);As,Ac分別為單根鋼管混凝土柱中鋼材截面面積和混凝土截面面積;f′c為混凝土圓柱體抗壓強度;fy為鋼材的屈服強度;fck為混凝土軸心抗壓強度標準值。

混凝土受壓本構模型如圖3所示。

2.1.2 混凝土受拉本構模型

由于鋼管與混凝土的接觸面并不牢靠,受拉時可脫開,因此鋼管圍套對混凝土受拉本構模型的影響較小,可采用普通混凝土的受拉本構模型,如式(2)所示。

(2)

混凝土受拉本構模型如圖4所示。

圖4 混凝土受拉本構模型

2.2 鋼材本構模型

鋼材以金屬材料力學性能試驗[7]的實測數據為基礎,采用“三折線”本構模型模擬循環荷載下的應力-應變關系,如圖5所示。

圖5 鋼材本構模型

2.3 加載制度

有限元模擬采用與驗證試驗[7]相同的加載制度。取B向(圖1)為位移的正方向,取B向的反向為位移的負方向,如圖6所示。在試件達到屈服位移Δ之前,取級差為Δ/3,每級荷載循環1次;當試件達到屈服位移Δ之后,取級差為Δ,每級荷載循環3次。

圖6 加載制度

2.4 有限元參數驗證

周婷[7]以1/2的縮尺比例設計了LCFT柱試件W5,并利用低周往復試驗對強軸向的抗震性能進行了研究。試件W5柱高1500 mm,柱肢長厚比n為3.5;單根鋼管柱截面尺寸為100 mm×100 mm,外包鋼板厚度為4 mm,軸壓比為0.3。采用上述有限元參數建立試件W5的ABAQUS有限元模型,并將計算結果與試驗數據進行對比,如圖7和表3所示:二者極限荷載相近,骨架曲線基本吻合;利用幾何作圖法求得的各項抗震性能評價指標基本相同,誤差低于10%。由此可知上述有限元參數可用于LCFT柱的有限元分析。

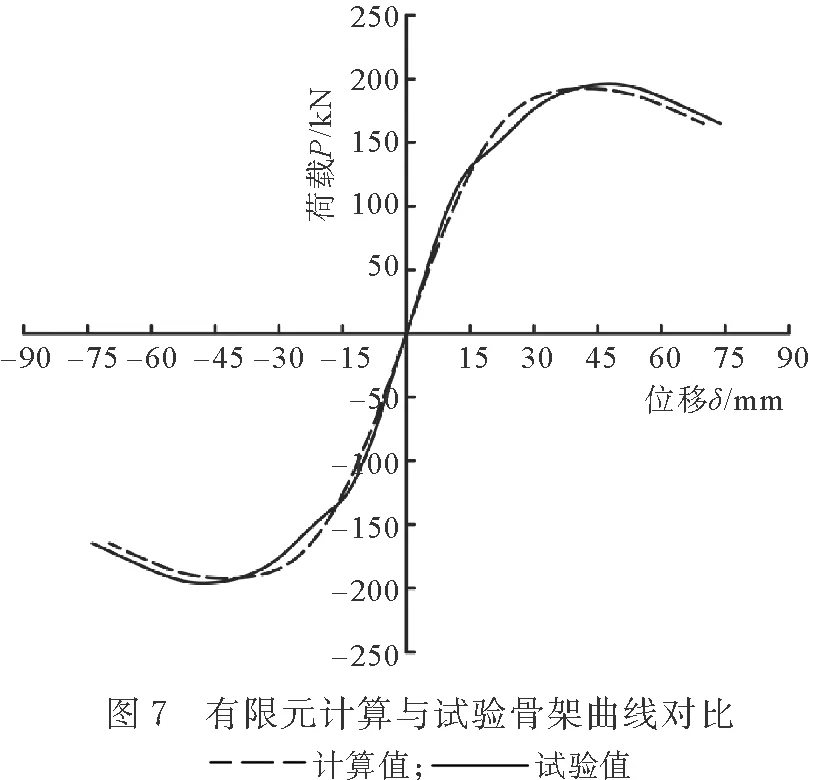
表3 有限元計算結果的誤差分析

3 破壞現象及數據整理

3.1 破壞現象

數值模擬表明,在B向低周反復荷載下,LCFT柱進入塑性階段后,犄角處的鋼管柱柱底鼓曲,連接鋼板變形,其破壞現象如圖8所示。

圖8 LCFT柱破壞云圖

3.2 骨架曲線

將27個試件的骨架曲線按照柱肢厚度的不同進行歸納整理:當柱肢厚度為180,200,220 mm時,各試件骨架曲線隨肢厚比n及方鋼管壁厚t的變化規律如圖9所示。

圖9 各試件骨架曲線

3.3 延性系數

依據骨架曲線,采用幾何作圖法[13]求得各試件的屈服位移Δy、極限位移Δu和延性系數μ(μ=Δu/Δy),如表4所示。

表4 各試件屈服位移、極限位移和延性系數

4 理論分析

由表4可知,當肢厚H及肢厚比n較小,方鋼管壁厚t較薄時,L形方鋼管組合異形柱弱軸向的抗震性能較差。通過相關性分析[14]簡化自變量的個數,再利用最小二乘法對表中數據進行二元二次曲線擬合[15]得各試件延性系數μ與肢長L、肢厚H、長厚比n及方鋼管壁厚t之間的關系,如式(3)所示。

(3)

由式(3)得,可通過調整肢長L和增厚方鋼管壁厚t的方式增大L形方鋼管組合異形柱弱軸向的延性系數,獲得與強軸向相近的抗震性能。除此之外,由表4可知,各試件的極限位移變化不大,均值為201.89 mm,極差僅7.7%,由此可得L形方鋼管組合異形柱弱軸向層間極限位移角約為1/15。

5 結論

1) L形方鋼管組合異形柱弱軸向的抗震性能較差,破壞模式以犄角處的鋼管柱柱底鼓曲,連接鋼板變形為主;延性系數μ與肢長L、肢厚H、肢厚比n及方鋼管壁厚t之間的關系為μ=1.7913×10-5L2-0.0205L+0.2069t+7.0595,其中L=nH。

2) 可通過調整肢長L和增厚方鋼管壁厚t的方式增大L形方鋼管組合異形柱弱軸向的延性系數,使其獲得與強軸向相近的抗震性能。

3) 當因建筑需求導致肢長L調整困難,或因增厚方鋼管壁厚t導致造價過高時,應驗算L形方鋼管組合異形柱框架結構弱軸向的層間位移角,最大值不應超過1/15。