基于非概率理論的引信MEMS安全與解除隔離裝置閉鎖機構可靠性評估

潘黎成,曹 云,2,雷勝洪,陸海寧,聶偉榮,席占穩

(1.南京理工大學機械工程學院,江蘇 南京 210094;2.重慶長安工業(集團)有限責任公司,重慶 401120)

0 引言

微機電系統(micro-electromechanical system,MEMS)技術是提升武器性能和降低成本最有效、最有發展前途的技術之一,美國國防部于1995年將MEMS技術在引信安全系統中的應用列為12項國防應用之首[1]。文獻[2—3]采用UV-LIGA工藝進行模塊化設計,研制出適用于25 mm高爆榴彈、20 mm空爆彈等中小口徑彈藥的MEMS引信安全與解除偏離裝置;文獻[4]設計制作了碳化鎢球驅動的MEMS安全與解除隔離裝置。當前對引信MEMS安全系統的研究已取得了較多成果,但就整體而言尚未能夠實現MEMS產品廣泛應用,可靠性問題成為制約其發展的關鍵因素[5]。

引信作為彈藥的關鍵部件,其可靠性和安全性直接影響戰斗部的毀傷效能。可靠性是指器件在規定時間內、規定條件下完成預定功能的能力,可靠度是可靠性的概率度量[6]。對引信小子樣可靠性評估已有相關研究,由于相關項目均涉及軍事機密,最新的前沿理論很難發現,從公開的研究結果來看主要分為三個方面:1) 貝葉斯方法與多源信息融合;2) 自主方法與系統仿真;3) 可靠性多級綜合方法[7]。三種方法均是采用場外同類樣本的實驗數據、仿真數據作為評估對象實驗數據的補充,而后采用概率方法進行系統可靠性的評估,其核心思想是貝葉斯理論。采用非現場實驗數據作為先驗信息,從一定程度上可以彌補實驗數據的不足。然而在很多時候尤其是軍工領域同類樣本的實驗數據獲得并不容易,而為了模擬真實的發射環境,進行仿真所耗費的計算資源和時間成本也很高,這就導致實驗數據從根本上來講比較貧乏。

采用概率可靠性評估方法進行分析需要大量的統計數據,當樣本不足時所得統計參數不足以精確描述結構特征的分布規律[8]。已有研究結果表明,在概率模型中某一系統的可靠度對于不確定參數所對應的統計參數的微小誤差非常敏感,設計不確定性的主觀假設可能會導致結構可靠性分析出現嚴重錯誤[9]。文獻[10—11]于1994首次提出一種用于描述不確定外界載荷或不確定幾何誤差所導致的器件失效的非概率凸模型,認為如果一個系統在發生故障之前所能容忍的不確定參數的波動幅度越大,那么該系統就越可靠。

目前,已有不少采用非概率理論進行可靠性分析的案例,取得了不錯的效果:文獻[12]采用非概率模型對飛機襟翼機構不對稱運動的安全性進行分析,該方法可以合理地評估系統的可靠性;文獻[13]采用區間非概率可靠性分析方法對復合材料高速轉筒在長期高載荷下的運動可靠性進行評估,在缺乏實驗數據或者僅能確定不確定參數變化區間時,可采用非概率可靠性評估方法,或者用該方法對概率可靠性方法進行有益的補充;文獻[14]針對履帶起重機工程實際中樣本量較小的問題,采用非概率理論建立臂架結構非概率可靠性模型;文獻[15]提出一種新的非概率時變可靠性模型,該模型可用于評估機構的運動可靠性;文獻[16]將響應面方法和非概率凸模型相結合,提出了一種可應用于復雜工程問題的結構可靠性分析方法。綜上所述,當樣本量不充分時,可考慮采用非概率理論對系統進行可靠性評估。

針對小樣本條件下傳統評估手段計算精度差的問題,本文基于非概率理論,提出引信MEMS安解裝置閉鎖機構的可靠性評估方法,并且結合薄板理論建立閉鎖機構區間非概率可靠性模型,得出非概率可靠性指標,之后進行區間變量的敏感性分析。

1 非概率理論簡述

在大多數情況下,不確定參數(如載荷、結構尺寸等)精確的統計規律是不易得到的,但是不確定參數波動變化的范圍是易于獲得的,由此引出區間理論。

若結構的不確定參數x在某區間范圍內變化,上界和下界分別為xu,xl,則x∈[xl,xu]屬于區間變量,對應的區間中點xc和區間半徑xr為

對區間變量x作標準化處理

x=xc+xrδ,

(2)

式(2)中,δ為標準化區間,δ∈[-1,1]。

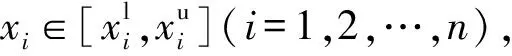
Z=g(X)=g(x1,x2,…xn)=
g(xr1,…,xro)-g(xs1,…,xsp)=
G(δr1,…,δro)-G(δs1,…,δsp),

(3)

式(3)中,g(X)為結構的功能函數在原始空間的表達;G(δ)為結構的功能函數在標準化區間內的表達形式;Xr={xr1,…,xro},δr={δr1,…,δro}為描述結構抵抗能力的不確定參數的區間變量;Xs={xs1,…,xsp},δs={δs1,…,δsp}為描述結構在外界載荷下響應的不確定參數的區間變量。

根據結構可靠性理論,當結構處于極限狀態時,失效面g(X)=0將結構區間變量空間分割為兩個部分,安全域g(X)>0和失效域g(X)<0。

文獻[17]指出,對于任意連續的功能函數Z=g(X)=g(x1,x2,…,xn),在標準化區間變量的拓展空間中,基于區間模型的非概率可靠性指標定義為按無窮范數‖·‖∞度量的從坐標原點到失效面的最短距離:

η=min(‖δ‖∞)。

(4)

文獻[18]已經證明對于線性功能函數,最可能失效點δ=(δ1,δ2,…,δn)位于標準化區間擴展空間內的對角線與失效面的某一交點上,滿足

η=|δ1|=|δ2|=…=|δn|。

(5)

以二維線性功能函數為例說明可靠性指標的含義,如圖1所示。

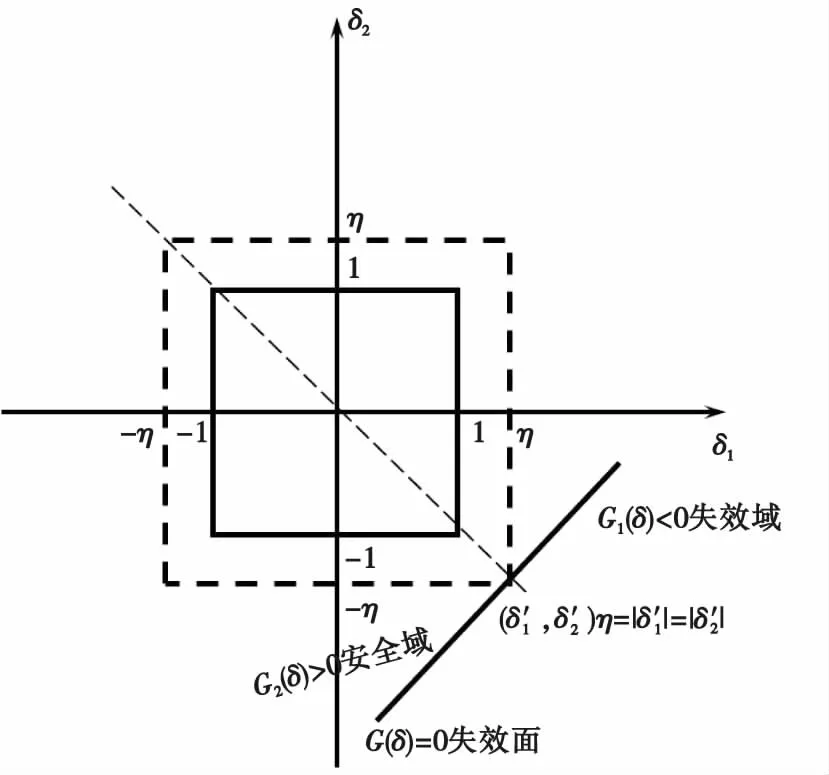
圖1 二維線性功能函數非概率可靠性指標Fig.1 Two-dimensional linear functional function non-probability reliability index

而對于非線性功能函數,可靠性指標的求解則轉化為如下的最優化問題:

以二維非線性功能函數為例進行說明,如圖2所示。

圖2中所示兩個極限狀態函數G1(δ)=0,G2(δ)=0,與線性功能函數不同的是,最可能失效點不一定位于角點,有可能位于極限狀態函數的某一切點,如圖所示最可能失效點分別為A、B,相應的可靠性指標為A、B坐標分量的最大值。

圖2 二維非線性功能函數非概率可靠性指標Fig.2 Two-dimensional nonlinear functional function non-probability reliability index

2 閉鎖機構可靠性模型

2.1 MEMS安全與解除隔離裝置整體方案

本文所研究的MEMS安全與解除隔離裝置適用于中大口徑榴彈彈丸。其發射環境主要分為加速度幅值12 000g、脈寬為4～6 ms的后坐環境以及出炮口轉速為ω=9 000 r/min的離心環境。其結構如圖3所示。

圖3 MEMS安解裝置整體示意圖Fig.3 Overall schematic diagram of MEMS S&A device

MEMS安全與解除隔離裝置主要由后坐保險機構、離心保險機構、指令鎖保險機構、隔爆滑塊以及閉鎖機構組成。MEMS安全與解除隔離裝置垂直彈軸安裝,當彈丸正常發射時,后坐保險機構向下運動解除第一道保險;同時在離心載荷的作用下,隔爆滑塊向右運動解除與離心懸臂梁的互鎖,離心保險機構在離心載荷的作用下解除第二道保險;此后隔爆滑塊繼續向右運動直至鎖鉤緊密抵住基板,當彈丸飛行至預期地點時指令鎖鎖鉤被微電推銷打彎,解除對隔爆滑塊的第三道保險;由于離心載荷的持續作用,隔爆滑塊繼續向右運動,帶動鎖頭撐開鎖鉤并且鎖定,隔爆滑塊運動到位,此時傳爆序列對正,引信完全解除保險,彈丸處于待發狀態。

由MEMS安全與解除隔離裝置運動原理可以看出,閉鎖機構的可靠性直接影響引信的傳爆序列在工作環境下能否可靠對正。若結構設計有缺陷,導致傳爆序列無法對正或者重合度不足會影響彈丸的毀傷效能,因此有必要對閉鎖機構的可靠性進行評估。

隔爆滑塊在離心載荷的作用下向右運動撐開鎖鉤的過程中,鎖鉤可能存在兩種失效模式:1) 閉鎖機構尺寸、結構等設計不合理,在離心載荷下鎖鉤無法撐開,無法完成“閉鎖”這一功能,稱為“功能失效”;2) 鎖鉤被撐開,完成了“閉鎖”這一功能,但此時鎖鉤已經屈服,發生塑性變形,這可能會導致傳爆序列無法對正,稱為“強度失效”。當器件的強度和功能均滿足要求時才認為結構是可靠的。

2.2 閉鎖機構強度可靠性

MEMS安全與解除隔離裝置閉鎖機構的強度可靠性指:滑塊在離心力作用下運動,帶動鎖頭撐開鎖鉤至最大限度時,鎖鉤不會發生屈服,此時認為該結構強度是可靠的。鎖鉤的設計尺寸如表1所示,其示意結構如圖4所示。根據彈性理論,兩個平行面和垂直于這兩個平行面的的柱面所圍成的物體稱為板。如果板的高度H小于B/8～B/5,可以將其稱為薄板[19]。所研究的鎖鉤其特征尺寸的比值為H/B=0.15,可近似為薄板。因此,鎖鉤內部應力狀態可以采用薄板理論進行分析。

表1 鎖鉤結構尺寸設計值Tab.1 Design values of locking hook structure size

2.2.1問題簡化

為了求解鎖鉤根部表面處的應力狀態,同時為簡化計算流程,先將該三維應力問題轉化為平面應變問題得出其在Z和X方向的位移,再按照薄板理論得出應力。鎖頭撐開鎖鉤的過程,可以看作是鎖鉤端部受到方向向上的均布荷載(另一個鎖鉤受力相反)。由于荷載不隨著Y方向發生變化,每個橫截面的位移是相同的,因此可以通過單位寬度橫截面的位移來近似計算鎖鉤的位移,從而求解應力。圖5所示為抽取出的橫截面。

圖4 鎖鉤示意圖Fig.4 Schematic diagram of the flexible locking arm

圖5 抽取出的橫截面Fig.5 Cross section

該單位寬度的鎖鉤由于被鎖頭擠壓而張開的位移為W,可以看作是在載荷P的作用下,端部最大位移為W。因此鎖鉤被撐開的過程轉化為鎖鉤端部在載荷P的作用沿Z方向位移W,求解此邊界條件下內部的應力。根據圣維南原理,在面力等效的情況下,遠處所受的影響可以忽略不計,鎖鉤根部處應力狀態不會發生太大改變,因此可將抽取的模型進一步簡化為一個懸臂梁,如圖6所示。

圖6 橫截面簡化為懸臂梁Fig.6 Cross-section simplified to cantilever beam

2.2.2應力求解

按照平面應變問題,求解懸臂梁的位移。選取二次應力函數和四次應力函數[20]:

根據材料力學基本假設,梁Z方向擠壓應力忽略不計,即σz=0。取二次應力函數為均勻剪應力荷載,即c2=0,a2=0,采用疊加原理,將二次應力函數所對應載荷與四次應力函數適當結合可得平面問題下各應力分量分別為

邊界條件為

(10)

因此得到平面問題下各應力分量和應變分量為

得到平面問題下梁上各點Z方向的位移為

根據前文彈性理論的假設,在Y方向上各個橫截面的位移均是相同的,薄板位移與y坐標無關,且根據板殼理論,在中面的任一根法線上,薄板沿厚度方向所有各點均具有相同的位移w,薄板上沿厚度方向各點的位移可由撓度近似為

應力分量τzx,τzy,σz遠小于其余三個應力分量,其對應的應變可以忽略不計。可得到鎖鉤根部表面處應力為

根據式(16)可求得各主應力如式(17)所示。

式(17)中,P為鎖梁端部荷載,P=3EI1W/L3。

梁根部表面處的等效Von-Mises應力為

式(18)中,μ、E分別為電鑄鎳泊松比以及彈性模量,W、H、L分別為鎖鉤載荷端Z方向位移、鎖鉤厚度以及其長度。

因此強度可靠性的功能函數為

式(19)中,σs、ns分別為電鑄鎳的屈服強度和安全系數,ns=1.2。

2.3 閉鎖機構功能可靠性

根據能量守恒原理,離心力對滑塊所做功轉化為彈簧的彈性勢能、鎖鉤應變能以及滑塊的動能,如果在離心載荷的作用下滑塊運動到閉鎖梁張開的極限位置時其動能仍然大于0,表明離心載荷仍有余能為滑塊提供動力,促使滑塊經過鎖鉤,該結構的功能可靠性達到要求。

設炮彈出膛口轉速為ω,離心力對隔爆滑塊所做功為

(20)

式(20)中,m為隔爆滑塊的質量,ω為炮彈出膛口轉速,d為靜止時隔爆滑塊質心與炮彈轉軸的距離,D為閉鎖后質心與轉軸的距離。

微彈簧的彈性勢能為

式(21)中,k為微彈簧剛度。

在薄板的小撓度彎曲問題中,不計應變分量εz,γyz,γxz,因此彈性體的應變能為

(22)

得到

式(23)中,B為鎖梁的寬度,其余各個參數與式(18)內的參數含義一樣。

因此功能可靠性的功能函數為

g2=QFω-Qs-Vε。

(24)

2.4 可靠性指標求解

采用光學顯微鏡對一批樣件共10個樣本的閉鎖機構關鍵部件進行拍攝,然后測量。由于顯微鏡視場較小,無法將鎖鉤完全拍下,因此分為兩次拍攝,之后采用SIFT算法對其進行拼接。圖7所示為某樣本的一對鎖鉤。

圖7 光學顯微鏡拍攝的鎖鉤Fig.7 Locking hooks photographed by optical microscope

文獻[21]對電鑄鎳膜進行拉伸實驗,獲得其彈性模量E和屈服極限σs。采用圖像處理軟件ImageJ對鎖鉤長度L和鎖鉤厚度H進行測量。對于同一批樣件而言,UV-LIGA工藝使用同一塊晶圓生產,鎖鉤寬度B可認為是不變的。鎖鉤的結構和材料參數如表2所示。

根據表2將功能函數g1、g2進行標準化,如下所示:

式(25)中,E=82+3δE,W=111.95+10.54δW,H=120.105+5.325δH,L=1 870.21+53.35δL。

表2 鎖鉤參數及其變化區間Tab.2 Locking arm parameters and their variation intervals

根據非概率可靠性指標定義,非概率可靠性指標η的求解可以轉換為如下的最優化問題:

文獻[22]指出工程實際中功能函數的響應可能非常復雜,如果采用梯度迭代的方法可能會得到不準確的可靠性指標,采用帝國競爭算法(ICA)可以不用考慮復雜功能函數的梯度,之后的數值算例也證明ICA與遺傳算法、粒子群算法相比結果更優。因此本文也采用ICA,得出非概率可靠性指標為η1=1.577 6>1,η2=18.034 2>1。根據非概率可靠性指標的含義,η1表明在這一批樣本下,鎖鉤強度可靠性極限狀態函數遠離變量區間,在張開的過程中鎖鉤內最大應力始終小于電鑄鎳屈服極限,該閉鎖機構在運動過程不會發生塑性變形;η2則表明功能可靠性極限狀態函數遠離變量區間,離心載荷對隔爆滑塊所做的功在轉化為彈簧的彈性勢能以及鎖鉤的應變能后,仍然留有很大余量作為隔爆滑塊的動能,促使滑塊通過鎖鉤。綜合上述,僅從數學意義上而言,兩種非概率可靠性指標表明,當鎖鉤的結構參數在如表1所示的變量區間內變動時可以實現可靠閉鎖,其功能是可靠的。

2.5 區間變量的敏感性分析

根據非概率可靠性分析方法得出了引信MEMS安全與解除隔離裝置閉鎖機構的可靠性指標之后,可根據該指標初步了解到所設計的結構的可靠程度。但是如何根據可靠性指標來指導后續的優化設計,還需要對區間變量進行敏感性分析,從而定量判斷出設計參數在區間內變化時對于結構響應的影響程度[23]。對于區間變量來說可采用區間敏感性分析方法。把表征不確定性的區間敏感性因子[24]定義為

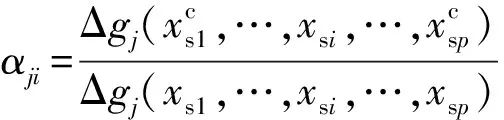
(26)

區間敏感性分析所表達的是設計變量區間的變化程度對結構響應區間的影響程度。|αji|越大,表明第j個結構響應對于第i個不確定參數的敏感性就越強,反之則越弱。通過閉鎖機構的強度可靠性功能函數以及功能可靠性功能函數,結合區間敏感性因子,可以定量判斷出當不確定參數在區間內波動時對閉鎖機構的結構響應(應力、能量)的影響程度。

對不同量綱的不確定參數進行敏感性分析時須先進行量綱統一或者對參數進行一定的轉化[27]。引入一個中間變量:變異系數,用于表征不確定參數的波動變化范圍,同時對參數進行量綱統一。與概率論中的變異系數CV相類似, CV越小,表明不確定參數波動變化范圍越小,越接近中值。變異系數可以表示為

通過對閉鎖機構2種失效模式下區間敏感因子的計算,給出了不確定參數的變異系數在0.01～0.8之間的結構響應敏感因子的變化曲線,如圖8和圖9所示。

圖8 應力敏感因子隨變異系數的變化曲線Fig.8 Variation curve of stress sensitivity factor with coefficient of coefficient of variation

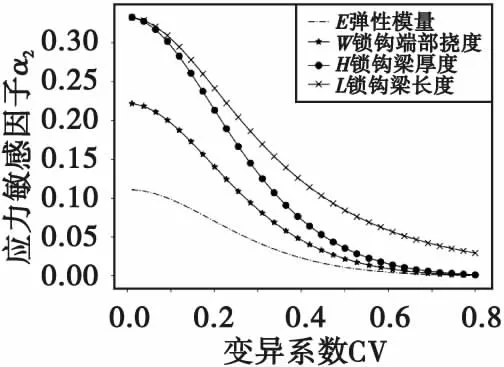
圖9 能量敏感因子隨變異系數的變化曲線Fig.9 Variation curve of energy sensitivity factor with coefficient of coefficient of variation

由圖8—圖9可以看出隨著變異系數的增加,各個不確定參數對于結構響應的影響逐漸變弱,即隨著不確定參數區間的逐步擴張,單個不確定參數對于結構響應的影響越來越小,此時需要綜合考慮多個不確定參數對結構的影響。

圖8中,不確定參數彈性模量E,鎖鉤端部撓度W以及鎖鉤梁厚度H的應力敏感因子α1之間的關系為α1E≈α1W≈α1H?α1L。

彈性模量、鎖鉤端部撓度以及鎖鉤梁厚度這3個參數對于結構響應的影響相當,而這3個參數應力敏感因子遠小于鎖鉤梁長度的應力敏感因子,并且隨著變異系數的增加,α1E、α1W、α1H趨近于0,表明此時這3個不確定參數對于結構的影響微乎其微。

圖9中,各不確定參數的能量敏感因子α2之間的關系為α2E<α2W<α2H<α2L。

彈性模量、鎖鉤端部撓度、鎖鉤梁厚度和鎖鉤梁長度這4個參數對于結構響應的影響逐步增加,并且隨著變異系數的增加,α1E、α1W、α1H趨近于0。

綜上所述,對于結構的設計優化應該這樣考慮,若引信MEMS產品生產制造時的工藝誤差較小,即變異系數較小時,E、W、H、L這4個不確定參數均對結構有較大的影響,但是不論從應力角度還是能量角度鎖鉤梁長度L對于結構響應的影響最大,在設計優化時應該優先考慮,之后考慮另外3個參數;若引信MEMS產品生產制造的工藝誤差很大,即變異系數很大時,圖中可以看出E、W、H對于結構的影響微乎其微,L占據主導地位,此時主要考慮鎖鉤梁長度L。

但是在實際生產過程中不會有這么大的工藝誤差,結合表1可知變異系數最大為0.094 1,現假設工藝誤差較大的情況:將變異系數放寬至0.15。綜合考慮圖8和圖9可以得知在對引信MEMS安解裝置閉鎖機構進行設計優化時優先考慮鎖鉤梁長度L以及鎖鉤梁厚度H,輔助以彈性模量E、鎖鉤端部撓度W比較合適。

3 閉鎖機構可靠性測試及分析

3.1 離心實驗

采用離心實驗平臺對2.4節中測量的10個樣本進行離心閉鎖實驗,驗證10個樣本閉鎖機構的可靠性。由于引信在炮彈上真實的安裝位置距離轉軸很近,轉盤無法達到相同的安裝條件,因此將MEMS安解裝置偏置一段距離r,根據離心轉盤的轉速和偏置的距離來獲得等效轉速,進而模擬炮彈發射時的離心環境。

基于離心旋轉臺進行離心實驗平臺的搭建,實驗平臺如圖10所示,已裝配樣機的夾具通過螺釘安裝在離心轉盤上,安裝時將離心轉盤半徑與樣機對稱中心線保持一致。

圖10 離心實驗平臺Fig.10 Centrifugal experimental platform

根據轉盤轉速,可得隔爆滑塊所受的離心加速度為

式(28)中,n為離心轉盤的轉速,r為隔爆滑塊質心相對于離心轉盤圓心的距離,本次實驗選取r=57 mm。

由于MEMS器件存在生產誤差,每一個樣本的特征尺寸與設計值存在誤差,每一個樣本的閉鎖情況都不相同。為了確定每一個樣本的閉鎖機構從未能閉鎖至閉鎖的臨界轉速,針對實驗樣本,每次實驗只取一個樣本安裝于離心實驗平臺。實驗初始施加2 700 r/min的轉速,觀察到隔爆滑塊鎖頭運動并頂住了鎖梁,但是并未閉鎖。此后對轉盤依次增大50 r/min轉速,觀察其閉鎖情況。閉鎖機構離心實驗后狀態如圖11所示,實驗結果如表3所示。

圖11 離心實驗后閉鎖機構狀態Fig.11 Status of latching mechanism after centrifugal experiment

3.2 實驗結果分析

實驗結果表明,MEMS安全與解除隔離裝置閉鎖機構在平均等效轉速10 309 r/min時能實現可靠閉鎖,表現出良好的閉鎖一致性,這一結果與預期的出膛口轉速在9 000 r/min以上的設計目標相符合,并且在閉鎖成功后柔性鎖梁沒有發生塑性變形。這一批樣本均能實現可靠閉鎖,這與非概率可靠性理論所評估出的結果一致,表明了采用非概率可靠性理論對MEMS安全與解除隔離裝置閉鎖機構進行可靠性評估的有效性。

4 結論

本文將MEMS安全與解除隔離裝置的不確定參數看作是區間變量,采用非概率理論對MEMS安全與解除隔離裝置閉鎖機構進行可靠性評估,建立閉鎖機構區間非概率可靠性模型。該方法從一定程度上彌補了工程實際中MEMS安全與解除隔離裝置樣本量稀少,概率可靠性模型難以建立的缺陷。之后將可靠性指標的求解轉化為一個最優化問題得出其指標,并且進行區間變量的敏感性分析。最后進行離心實驗模擬炮彈發射時的離心環境,實驗結果與非概率可靠性理論評估的結果具有很高的一致性,表明非概率理論對MEMS安全與解除隔離裝置可靠性評估具有較好的適應性,可為后續的引信MEMS安全與解除隔離裝置可靠性分析提供參考。