基于BP神經網絡PID的水下無人航行器舵機驅動智能控制系統

張肖江,周春桂,王志軍,王小東,侯一方,張卓毅

(中北大學機電工程學院,山西 太原 030051)

0 引言

在現代海戰領域的研究中,水下自主航行器受到了越來越多的關注。舵機作為水下航行器的重要組成部分,直接影響了航行器的總體控制性能[1]。目前選用低損耗、大扭矩的永磁同步電機已經成為水下舵機選型的趨勢。但由于永磁同步電機是高階非線性系統,控制效果受到電機參數、海浪等因素的干擾較大。應用較為廣泛的傳統PID雖然簡單易于實現,但面對復雜非線性時變系統時,不具有重新整定參數的能力。為了解決傳統PID動態響應特性差的問題,文獻[2]提出了變論域模糊PID控制器,相較于傳統PID,提高了控制精度,但模糊控制需要一定的專家經驗,并未驗證其抗干擾性。文獻[3]采用滑膜控制,提高了控制精度,有一定的抗干擾性,但是滑模控制在穩定后會造成抖震。BP(誤差反傳)神經網絡對復雜非線性系統具有很強的自適應、自學習的能力。文獻[4]提出了將BP神經網絡和PID控制器結合的方法,實現了對永磁同步電機的調速;但是由于標準BP神經網絡在修正權值時是按負梯度方式修正的,容易使學習過程陷入局部震蕩、收斂速度慢的情況。

本文針對基于PID控制的電機調速舵機系統無法自學習、自適應的局限性,將PID控制器與BP神經網絡算法相結合,引入動量項,減少震蕩,設計了基于BP神經網絡PID控制器,并建立了不同控制輸入信號下偏航通道和舵機的整體仿真。

1 水下航行器控制系統及BP神經網絡PID算法

1.1 水下航行器控制系統結構

水下航行器偏航通道的控制系統如圖1所示,主要由偏航通道控制器、舵回路、舵片、航行器以及反饋裝置等組成,其中舵回路由舵回路控制器、電機、反饋裝置和減速器組成。當舵機控制器接收到控制輸入和舵機位置的偏差信號后,驅動電機轉動,隨后經減速器減速后由反饋裝置傳回比較器構成舵回路閉環。對于偏航通道控制系統,由控制輸入與實際的偏航角產生的偏差信號經過偏航通道的控制器生成響應的控制信號加到舵機上,舵機推動舵片轉動,從而操縱航行器運動,使航行器達到并保持在新的航向設定上[5]。

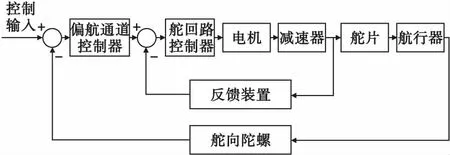
圖1 水下航行器控制系統框圖Fig.1 Block diagram of an underwater vehicle control system

電機作為航行器舵機動力系統的主要組成部分,控制效果的好壞直接決定著航行器的運動姿態好壞。永磁同步電機因其結構簡單、體積小、效率高逐漸成為伺服電機系統的發展趨勢[6]。

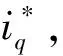
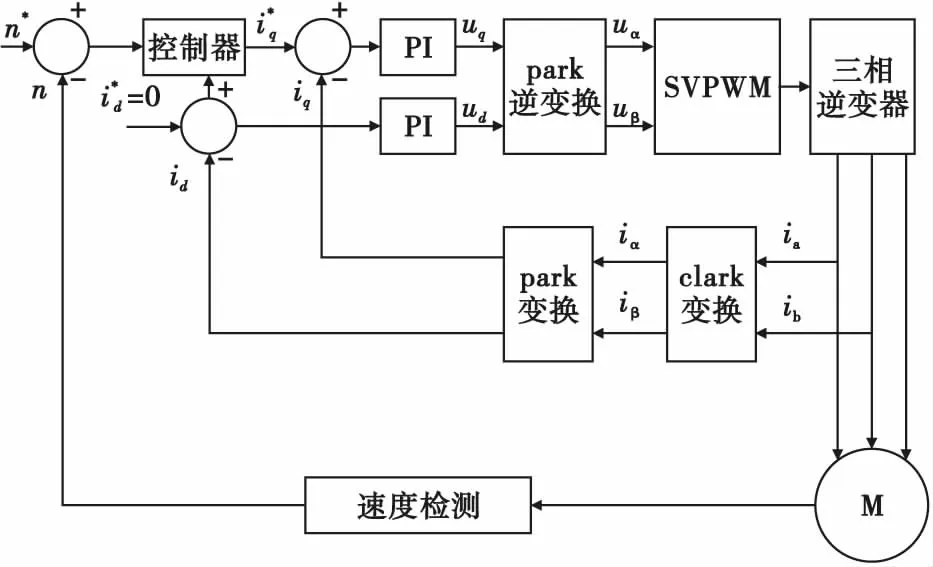
圖2 永磁同步電機控制系統框圖Fig.2 Block diagram of a permanent magnet synchronous motor control system

1.2 BP神經網絡PID算法

本文設計的控制器是基于BP神經網絡PID的控制算法。傳統PID控制是對被控對象進行閉環控制,比例、積分、微分三個環節環環相扣,互相制約,但不具備參數自學習的能力;而BP神經網絡可以對函數進行映射,有很強的自學習和自適應能力。兩者相結合,可以使KP,KI,KD三個參數的各種非線性組合得到最優解,取代人的經驗調參,實現對復雜系統的實時控制。BP神經網絡PID控制結構器框圖如圖3所示。圖3中的神經網絡控制器由增量式PID控制器和神經網絡兩部分組成。

經典增量式PID控制算法公式為

u(k)=u(k-1)+KP[e(k)-e(k-1)]+
KIe(k)+KD[e(k)-2e(k-1)+e(k-2)],

(1)

式(1)中,KP為比例系數,KI為積分系數,KD微分系數,e(k)為第k次采集的誤差值,e(k-1)為k-1時刻采集的誤差值,e(k-2)為k-2時刻采集的誤差值。

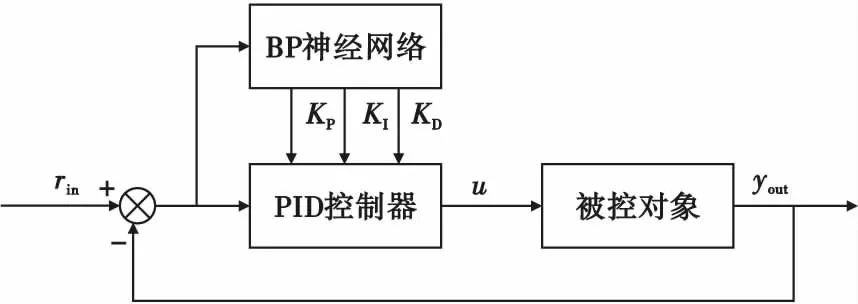
圖3 BP神經網絡PID控制結構Fig.3 BP neural network PID control structure

2 基于BP神經網絡PID控制器

根據原理的描述,BP神經網絡PID算法如下[10]:

1) 初始化:確定各層的神經元節點個數以及各層級之間的權值,并賦予(-1,1)之間的隨機值。有時為了訓練的效率可以對原始數據樣本機型規范化處理。

2) 前向網絡計算:BP神經網絡的輸入輸出為

隱含層的輸入為

(3)

隱含層的輸出為

f(x)為雙曲正切函數,即

輸出層的輸入為

(6)

輸出層的輸出為

由增量式PID(式(1))可得控制器輸出u(k)。

3) 采取輸出誤差二次方為性能指標函數

若誤差小于等于事先設定的值,則算法結束;否則誤差反向傳遞,按照梯度下降法,逐層修改權值。

4) 采用梯度下降算法使得網絡權值系數按照學習率η修正,使搜索快速收斂至全局極小,由此可得到權值更新計算公式為

g′(x)=g(x)[1-g(x)]。

(15)

隱含層連接權值更新為

f′(x)=1-f2(x)。

(18)

5) 令k=k+1,將權值返回至第2)步重新開始計算,若性能指標函數E(k)滿足設定值,則結束學習;反之,繼續學習。

標準的BP神經網絡采用梯度下降法作為主要手段權重沿著梯度下降的反方向修正,如果得不到期望輸出,則將誤差信號返回,據此對各項參數進行修改;如此反復交替,直到到達收斂為止。但在修正權值ω(k)時只是按負梯度方式修正,未考慮之前學習到的經驗,常常會使系統陷入局部最小,引起局部震蕩,收斂緩慢,為此引入動量項,如式(19)所示:

ω(k+1)=ω(k)+αω(k-1)+ηδo,

(19)

式(19)中,ω(k)為權值,α為動量系數,η為學習率。

BP神經網絡PID控制器模型,如圖4所示。BP神經網絡結構設計及算法選擇對于網絡性能有著重要影響,以給定轉子角速度r(k)、實際轉子角速度y(k)、轉子角速度偏差e(k)及其延時信號作為網絡輸入,u(k),KP,KI,KD,更新權值作為網絡輸出。設定隱含層節點數為8,網絡學習率η=0.01,動量系數α=0.3,以性能指標E(k)作為評價指標[11]。

圖4 BP神經網絡PID控制器Fig.4 BP neural network PID control structure

3 仿真驗證

3.1 電機仿真

基于圖3的矢量控制系統和1.2節中的BP神經網絡PID算法控制,在Matlab/Simulink中建立永磁同步電機模型,如圖5所示。電機參數如表1所示。

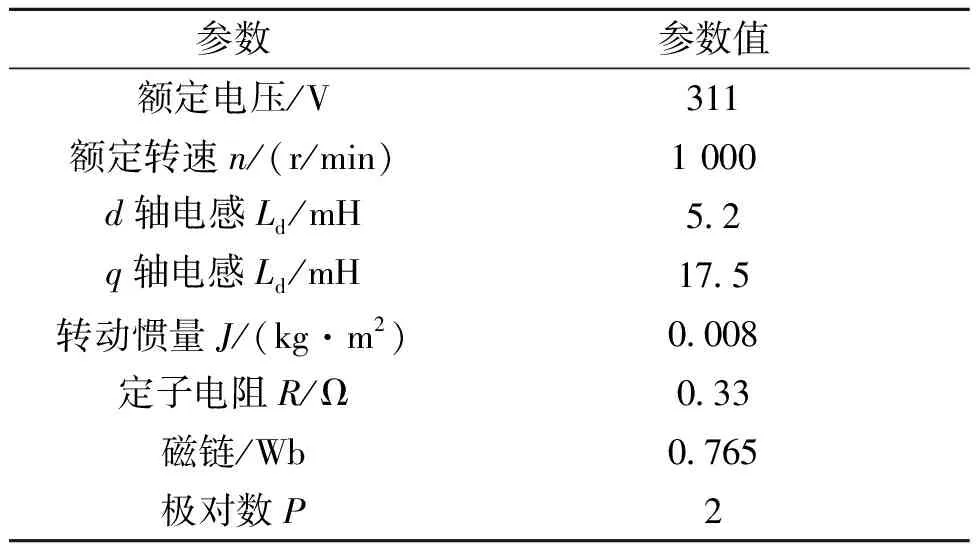
表1 電機工作參數Tab.1 Motor operating parameters

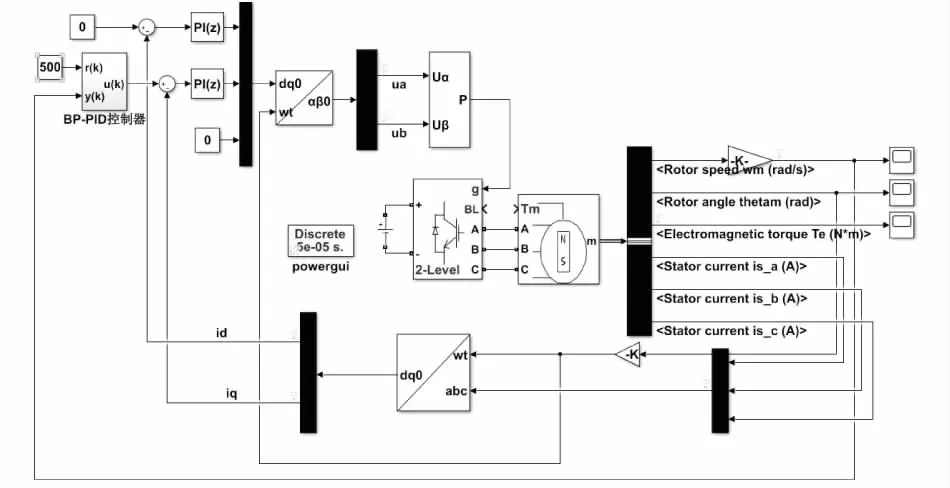
圖5 永磁同步電機調速系統仿真模型Fig.5 Simulation model of permanent magnet synchronous motor speed regulation system

當控制轉速為500 r/min,并在0.2 s時加入一個幅值為5,作用時間為0.1 s的脈沖干擾信號來模擬負載的變換。轉速響應曲線如圖6,結果對比如表2所示。

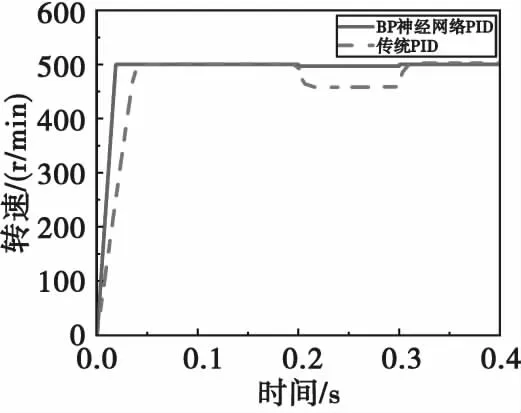
圖6 轉速響應曲線Fig.6 Response curve of velocity

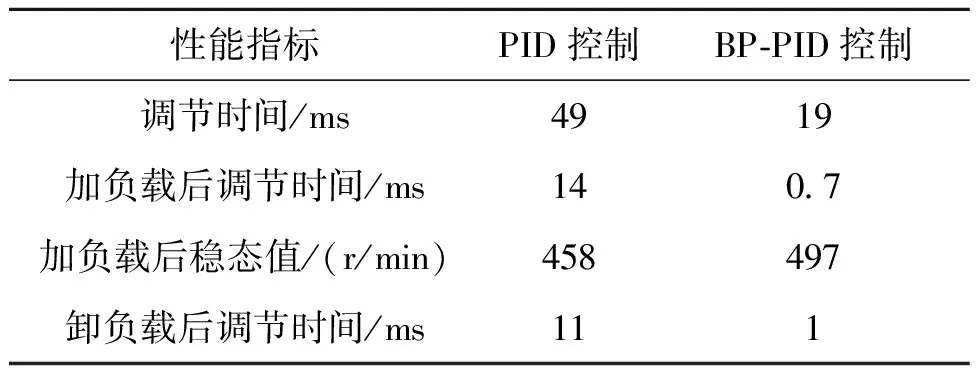
表2 加入脈沖干擾后結果對比Tab.2 Control performance indicators after pulse interference

由圖6和表2結果可知,BP神經網絡PID控制器達到穩態的時間要比傳統PID快61%左右,兩種控制方法都無明顯超調。但在0.2 s后加入脈沖干擾后,BP-PID在0.7 ms后穩定在497 r/min左右,而傳統PID需要14 ms后才可以到達穩態值470 r/min。在卸負載后,BP神經網絡PID相較于傳統PID控制調節時間快了90%左右。

3.2 舵回路及偏航通道仿真

為驗證基于BP神經網絡的永磁同步電機調速系統的正確性,建立舵機回路模型,如圖7所示。

圖7 舵機控制系統Fig.7 Steering gear control system

當加入8°的舵角指令,分別對比傳統PID與BP-PID的控制性能,得出8°信號下舵機角度曲線及結果對比,如圖8和表3所示。

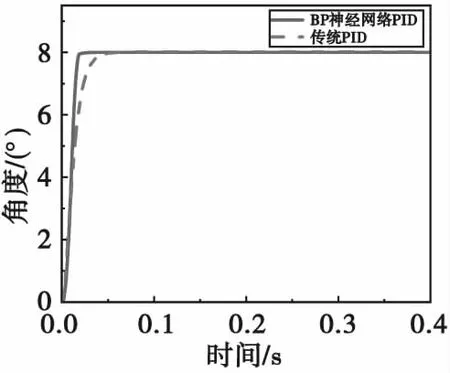
圖8 8°信號下舵機角度曲線Fig.8 The curve of servo angle under 8°signal

由圖8和表3可知,兩種控制方法都有較好的動態響應能力,但BP神經網絡PID控制器達到穩態的時間要比傳統PID控制快65%左右。

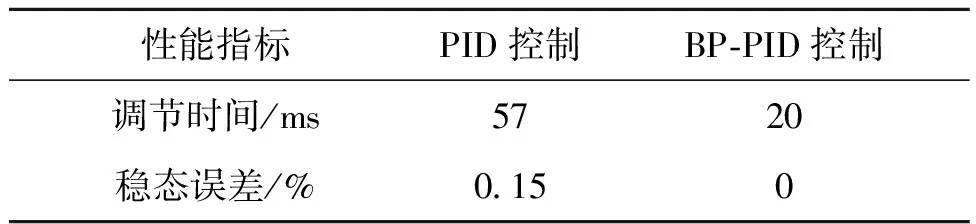
表3 控制輸入為8°時舵機角度結果對比Tab.3 Comparison of servo angle resultswhen the control input is 8°

為進一步驗證基于BP神經網絡PID電機調速系統的優越性,對某型水下航行器做偏航通道仿真模擬,如圖9所示。

其中偏航通道的傳遞函數為

偏航運動由尾部的垂直舵盤控制,使用指數函數,經過拉氏變換后可得[12]

輸入分別給定一個8°的航向角和正弦信號,進行仿真分析,得出8°信號下航向角曲線和結果對比,如圖10和表4所示。

圖9 水下航行器偏航通道控制系統Fig.9 Yaw channel control system for underwater vehicles

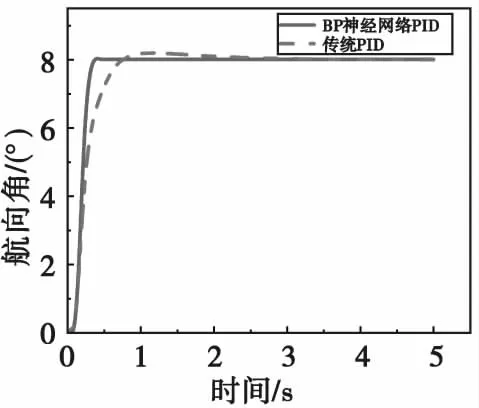
圖10 8°信號下航向角曲線Fig.10 The curve of heading angle under 8°signal

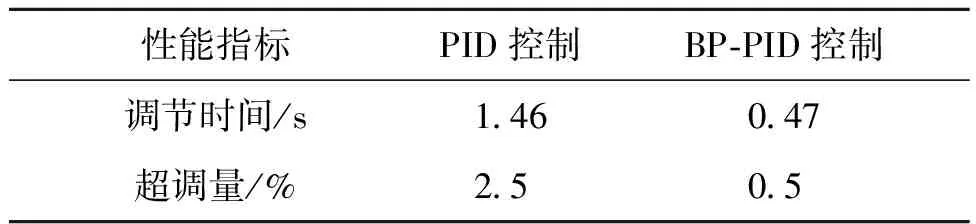
表4 控制輸入為8°時航向角結果對比Tab.4 Comparison of heading angle resultswhen the control input is 8°

由仿真結果可知,在8°航向角的輸入下,BP神經網絡PID控制器比傳統PID的超調量少了2%,調節時間快了1 s左右。

為了驗證系統跟隨性,輸入幅值為1的正弦信號,進行仿真分析,結果如圖11和表5所示。

由圖11和表5可知,在正弦信號作為輸入信號的情況下,BP-PID控制的上升時間比傳統PID的快40 ms,相位誤差比傳統PID少46%左右。

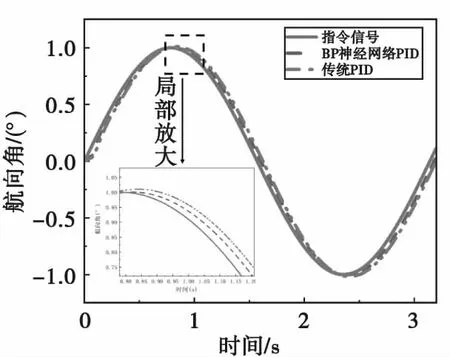
圖11 正弦信號下航向角曲線Fig.11 The curve of heading angle under sinusoidal signal

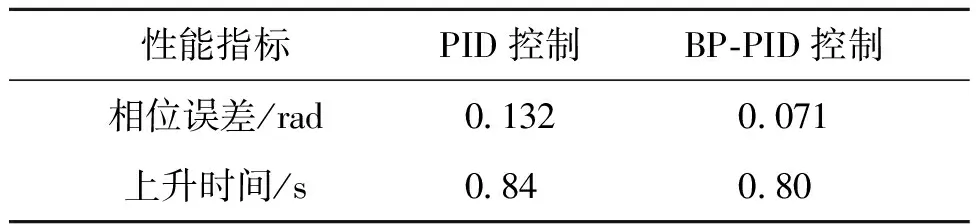
表5 控制輸入為正弦信號結果對比Tab.5 A control input of sinusoidal signal result comparison

4 結論

針對傳統PID控制器會造成水下航行器舵機控制精度不高的問題,提出基于BP神經網絡PID控制器的電機調速系統,并在算法中引入動量項,減少了曲線局部震蕩,加速收斂。與傳統PID控制器相比,BP神經網絡PID控制器減少了曲線局部震蕩,加速收斂,具有更好的動態響應能力和抗干擾能力。仿真結果表明,相較于傳統PID控制,永磁同步電機在BP神經網絡PID的控制下,水下航行器舵機系統能達到更好的動靜態性能,對電機調速系統和水下航行器舵機控制有一定的參考價值。