單軸虛擬振動試驗技術研究

趙艷濤，陳耀，李健，賈俊杰

（航天科工防御技術研究試驗中心，北京 100854）

在開展實物振動試驗時，會有振動臺推力不夠、關心部位不易粘貼傳感器而不能獲得其振動情況、實物試驗周期太長、實物試驗驗證滯后等局限。虛擬振動試驗成本低，不受客觀條件限制，獲取數據全面，可以加快設計更新迭代、縮短設計周期、大型試驗前優化試驗方案等優點。虛擬試驗可以彌補實物試驗的種種不足而越來越受到重視。國外對虛擬振動的研究已經取得了不少成果，并在工程實際中開展應用。國內已經有多家單位開展了相關的研究，主要有有限元模型結合開環振動分析、建立振動臺有限元模型結合閉環振動控制等，但應用還有頻率范圍、試驗類別等諸多的限制。本文著眼于以有限元構建振動臺平臺的基礎上，結合隨機振動控制算法，搭建閉環隨機振動虛擬試驗系統，可以將經校準后的不同產品模型“安裝”在該系統中，開展隨機振動虛擬試驗，具有一定的通用性。

1 閉環隨機振動虛擬系統搭建

本文構建了閉環隨機振動虛擬試驗系統，虛擬振動整體系統如圖1 所示。振動臺系統簡化為振動控制系統和振動臺機械模型2 部分，其中功放系統和濾波放大電路可以分別測量各自的頻響函數[1]，再和振動臺機械部分的頻響函數聯合起來，構成系統的頻響函數，控制儀根據系統的頻響函數來進行振動控制。由PATRAN 建立振動臺有限元模型，并生成系統頻響函數文件，由MATLAB 讀取后進行整個控制計算。

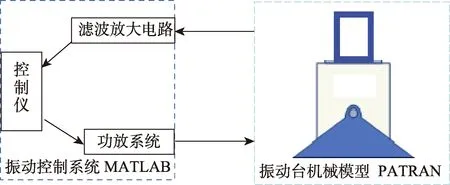
圖1 虛擬振動整體系統Fig.1 Diagram of overall virtual vibration system

1.1 控制儀模型[2-4]

隨機振動試驗的控制過程如圖2 所示。控制儀首先根據參考譜生成驅動譜，由驅動譜生成頻譜，經逆傅里葉變換后，得到偽隨機信號，并轉化為真隨機信號來驅動振動臺。將傳感器測量結果和參考譜進行比較后，生成下一次的驅動譜。

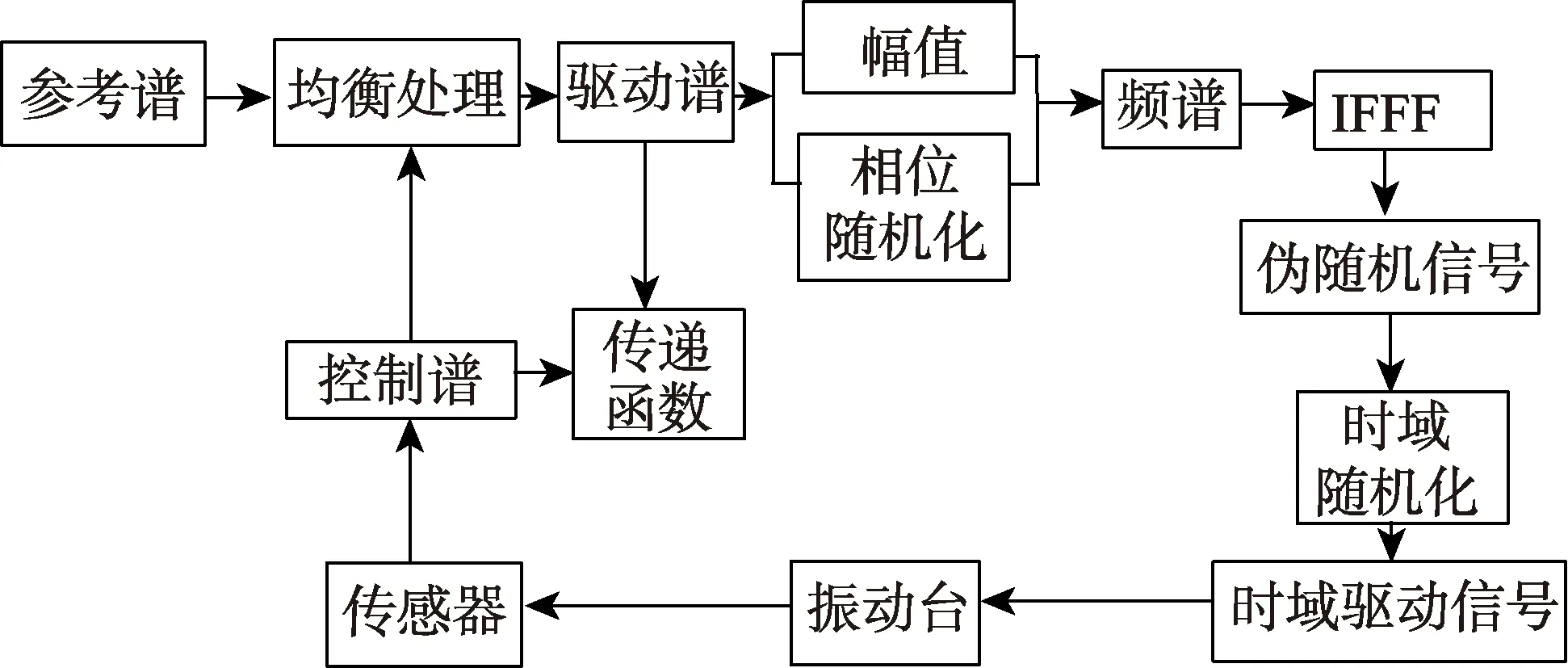
圖2 隨機振動虛擬試驗控制過程Fig.2 Control process of virtual random vibration test

1）頻響函數的估計[5]。頻響函數可通過式（1）得到[6]：

式中：PSDCD為驅動信號和響應信號的互譜，g2/Hz；PSDDD為驅動信號自譜，g2/Hz；H為系統的頻響函數。

2）隨機振動試驗控制中，由系統頻響函數和參考譜可得到如下驅動譜：

式中：PSDR為參考譜，g2/Hz；PSDD為驅動譜，g2/Hz。

由參考譜和當前的驅動譜得到下一次的驅動譜，如式（3）所示[7]。

式中：(PSDD)i為當前驅動譜；(PSDD)i+1為下一次的驅動譜；(PSDC)i為當前控制譜。

這是隨機振動的驅動譜（頻域）均衡迭代的核心算法，當然也還有其他的隨機振動控制算法，驅動譜轉化為時域驅動信號來驅動振動臺。

3）驅動譜（頻域）轉換為時域的驅動信號。由驅動譜可以得到驅動信號的幅值，單獨幅值信息不能夠轉換得到時域信號，因此進行相位隨機化后，將驅動信號的幅值再附加隨機的相位信息后，進行逆傅里葉變換，可以得到時域的偽隨機信號。偽隨機信號還不可以直接作為時域的驅動信號，需進行時域隨機化處理。對相位隨機化后的偽隨機信號經過延遲和反向后，得到多組時域信號，然后進行加窗疊加，就得到了可用于時域驅動信號的真隨機信號[8-9]。

時域驅動信號經過功放系統放大后，驅動振動臺中的運動部件運動，傳感器將加速度信號通過濾波放大電路傳遞給控制儀。控制儀根據當前傳感器測試得到的當前控制譜，結合參考譜和當前驅動譜，按照式（3）做迭代計算后，輸出下一次的驅動譜。

1.2 振動臺機械模型建模

1.2.1 振動臺幾何模型

振動臺主要包括動圈和臺體，動圈通過上懸掛彈簧和下導向軸承固定在臺體上，臺體通過空氣彈簧固定在底座上，如圖3 和圖4 所示。動圈是主要活動部件，產品通過夾具安裝在動圈上，動圈帶動產品運動。動圈主要包括骨架和線圈，線圈作為固定連接在動圈骨架上。通過建立有限元模型，并附加邊界條件來模擬振動臺。

圖3 振動臺整體模型Fig.3 Overall model of vibration table

圖4 動圈模型Fig.4 Moving coil model

1.2.2 動圈的有限元模型

動圈是振動臺的核心部件，采用有限元軟件對動圈進行網格劃分。劃分網格時，既要保證網格精度，又要兼顧計算效率，對不規則部分采用四面體網格劃分，對規則部分采用面單元進行網格劃分，如圖5 所示。

圖5 動圈及臺體的有限元模型Fig.5 Finite element model of moving coil (a) and platform (b)

動圈骨架和線圈之間連接的模態對應的特征頻率都遠在振動臺的工作頻率之外，對系統響應的影響比較小，將骨架與線圈間簡化為剛性連接，將動圈作為一個剛性整體。骨架為各向同性材料的鎂鋁合金，線圈作為驅動力的來源，既要導電又要降溫，其由銅導管繞制而成，銅導管本身導電，內部通過冷卻水來降溫，通過特種膠將銅導管粘接在一起，外部再通過鋼片粘接固定。為了方便分析，將線圈材料簡化為各向同性材料進行處理[10-12]。

在保證幾何模型與實物相符的前提下，來調整密度和彈性模量這2 個材料參數[13]，使模態仿真結果與模態試驗結果一致，即可認為此有限元模型可以用于虛擬振動。

1.2.3 動圈的邊界條件

動圈上端四周有4 個間隔90°的懸掛彈簧將動圈懸掛在臺體上，可以限制動圈的橫向振動和扭轉。另外，動圈中央豎直方向的剛性軸通過空氣彈簧連接在臺體上，上下懸掛系統都通過彈簧單元來簡化，僅保留軸向平動自由度，保證動圈沿豎直方向運動。中心剛性軸對動圈的導向作用通過多點約束單元（MPC單元）的來進行模擬，并約束其他所有自由度，而只保留豎直方向運動[14-15]。

臺體作為動圈的支撐系統，按照其幾何模型進行網格劃分。臺體通過空氣彈簧懸掛在底座上，如果工作頻率比較高，可以忽略空氣彈簧的影響；如果工作頻率比較低，則需要考慮空氣彈簧的影響，空氣彈簧可采用彈簧單元來簡化。

1.2.4 模態試驗驗證

分別對動圈、夾具、產品建立有限元模型，并結合模態試驗進行有限元模型校準。模態試驗中，分別對被試對象用橡皮繩懸掛后，采用錘擊法開展模態試驗，多次錘擊獲取有效數據后，通過PolyLSCF 法識別模態參數，再通過MAC 矩陣來驗證獲取的模態參數是否可信。在保證模態試驗結果可信的基礎上，修正有限元模型的過程如下：在幾何模型與實物相符的前提下調整材料參數，在參考材料基本參數的基礎上，首先微調密度來保證質量與實際質量一致[18]，再微調彈性模量，使模態仿真結果與模態試驗結果比較接近，主要模態頻率最大相對誤差在5%以內，使得振動臺各部分的材料參數能夠反映真實的材料特性，可認為有限元模型是可信的[16]。夾具模態仿真和模態試驗的主要模態頻率比對見表1，振型如圖6 所示。產品模態仿真和模態試驗的主要模態頻率比對見表2，振型如圖7 所示。動圈模態仿真和模態試驗的主要模態頻率比對見表3，振型如圖8 所示。

表1 夾具模態仿真和模態試驗模態頻率比較Tab.1 Comparison of modal frequencies of fixture modal simulation and modal test

圖6 夾具各階振型Fig.6 Various vibration modes of fixture: a) 1st order;b) 2ed order;c) 3rd order;d) 4th order;e) 5st order;f) 6th order;g) 7th order;h) 8th order

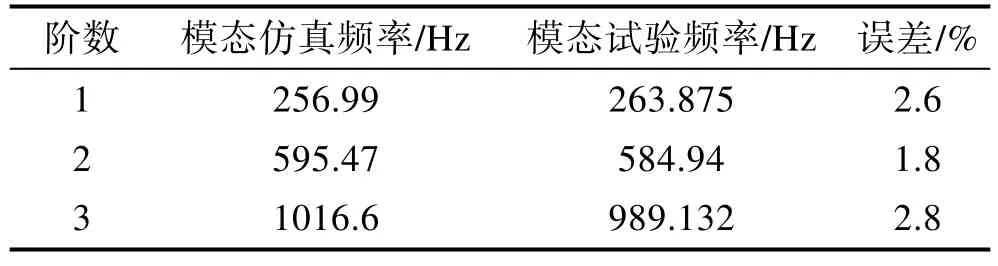
表2 產品模態仿真和模態試驗模態頻率比較Tab.2 Comparison of modal frequencies of product modal simulation and modal test

圖7 產品各階振型Fig.7 Various vibration modes of product: a) 1st order;b) 2ed order;c) 3rd order

表3 動圈模態仿真和模態試驗模態頻率比較Tab.3 Comparison of modal frequencies of moving coil modal simulation and modal test

圖8 動圈各階振型Fig.8 Various vibration modes of moving coil: a) 1st order(torsion);b) 2ed order (breathe);c) 3rd order (Telescoping)

實物試驗中，夾具與產品、夾具與動圈通過螺栓連接。開展產品虛擬振動試驗時，動圈與夾具、夾具與產品螺栓連接處，建模時通過剛性連接來代替螺紋連接。單元類型采用RBE2（剛體單元）[17]。將產品、夾具的有限元模型與振動臺的動圈模型進行連接，構成振動臺機械系統的有限元模型，結合隨機振動控制儀模型，構建整個虛擬振動閉環控制系統，進行虛擬振動閉環控制，來確定振動試驗控制方案、產品的振動量級等。

在進行模型修正時，首先根據模態試驗結果，在修正密度使模型與實物質量相符后，再調整彈性模量，使虛擬試驗和實物試驗在模態頻率和振型上一致，使模型的剛度矩陣、質量矩陣得到修正。其次，側重對結構阻尼、結構件之間的連接關系、邊界條件、彈性模量等參數進行反復修改，使測點的虛擬試驗與實物試驗結果一致。可參考文獻[18]中的方法進行分區和參數修改，可以快速修正目標，滿足工程需要，詳細過程見該文獻。

2 虛擬振動和實物試驗結果的比對

目標譜為梯形譜，譜形如下，20～80 Hz：+3 dB/Oct；80～350 Hz：0.04g2/Hz；350～2 000 Hz：–3 dB/Oct。均方根值6.06g。夾具為正方形板狀結構，產品通過夾具安裝在振動臺臺面上。選取靠近夾具4 條邊線的中點及中心點作為控制點（如圖9 所示），采用多點平均值控制。

圖9 振動控制點示意圖Fig.9 Diagram of vibration control points

選取產品上測量點為1#（位于產品頂圈壁面，對應節點542200）、2#（位于產品中圈壁面，對應節點542883），如圖10 所示。實物試驗及虛擬試驗結果比對分別如圖11、圖12 所示。

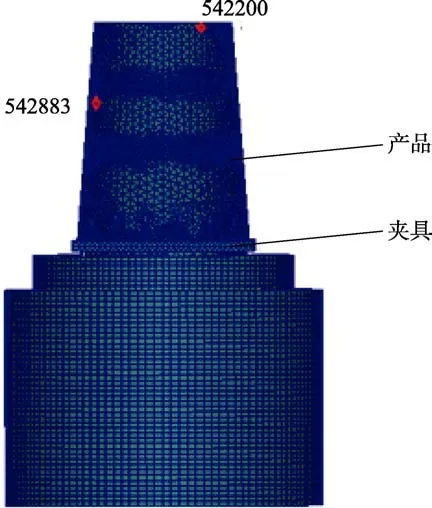
圖10 振動系統有限元模型及測量點Fig.10 Finite element model and measuring points of vibration system

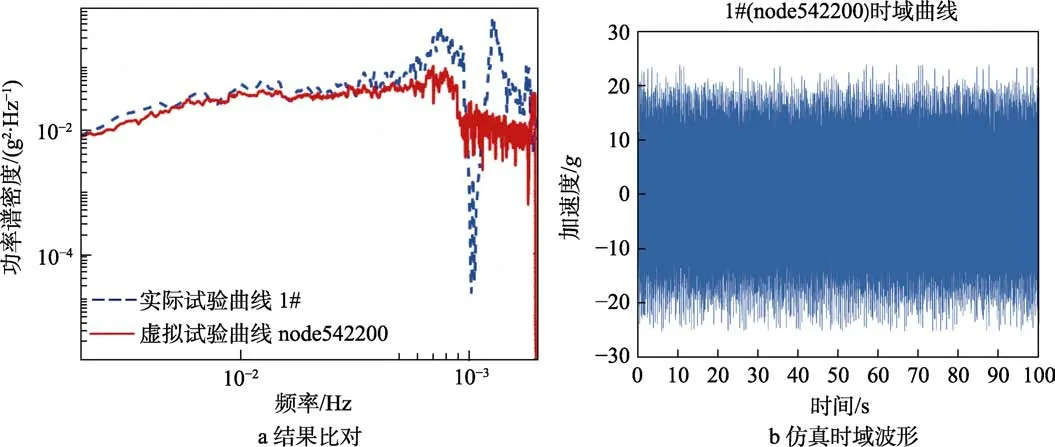
圖11 1#實物與虛擬試驗結果比對及仿真時域波形Fig.11 Comparison of 1# physical and virtual test results (a) and simulated time domain waveform (b)

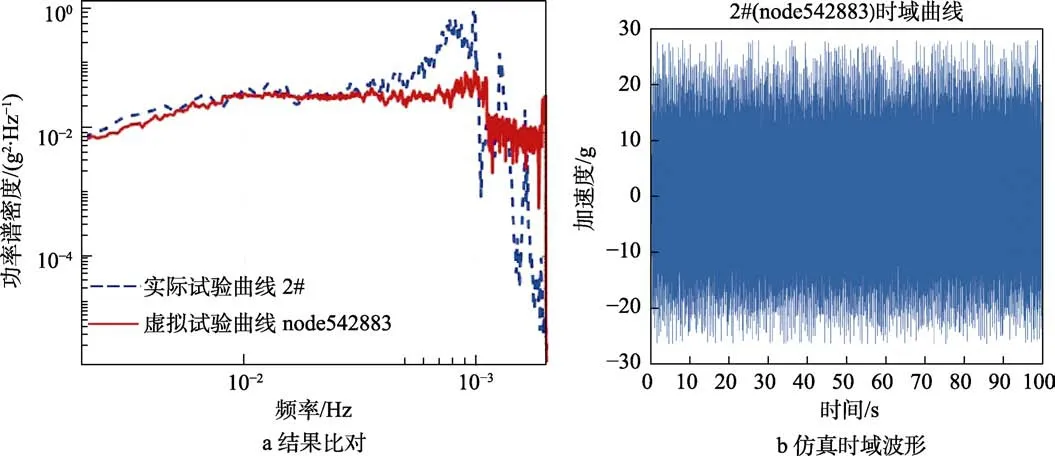
圖12 2#實物及虛擬試驗結果比對及仿真時域波形Fig.12 Comparison of 2#(node542883) physical and virtual test results (a) and simulated time domain waveform (b)

從表4 可以看出，400 Hz 以前，虛擬試驗和實物試驗的均方根值誤差明顯小于全頻段內的。另外，400 Hz 以內，1#的最大功率譜密度誤差為0.034g2/Hz，2#的最大功率譜密度誤差為0.038g2/Hz。在400Hz以上的高頻段內，功率譜密度誤差遠遠超過400 Hz前的低頻段。

表4 不同頻段實物試驗和虛擬試驗均方根值比較Tab.4 Comparison of root mean square values of physical test and virtual test in different frequency bands

通過比對實物試驗和虛擬試驗結果，由曲線的趨勢可以明顯看出，二者在400 Hz 之前的低頻段，整體趨勢一致性相對較好，在高頻段的一致性相對較差。這和高頻段模態比較復雜、隨機振動在高頻段難控制是一致的。在建模過程中，由于很多細節進行了簡化處理，會影響到高頻部分的仿真結果。另外，網格劃分受到計算機計算能力的限制，不能劃分足夠小的尺寸，也會影響到虛擬試驗高頻部分結果。同時，高頻段在實物試驗時難免會出現一定程度的非線性，但仿真計算是基于線性假設，這就難以保持二者在高頻段的一致[22]。

3 結語

結合有限元和閉環隨機振動控制方法搭建的隨機振動虛擬試驗系統在400 Hz 前的低頻段有相對較好的可信度，高頻段的虛擬試驗結果精度還有待提高。這種方法搭建的隨機振動虛擬振動系統的虛擬振動是一個比較復雜的過程，涉及到許多的技術細節，以上只是初步的工作，想要虛擬振動試驗系統通用性更強，得到更準確的結果，則需要進一步進行詳細建模和修正。另外，本文只進行了虛擬振動的初步探索，后續可結合工程實踐進一步完善和推廣應用。

1）單軸虛擬振動是雙臺振動和多維振動的基礎，在單軸虛擬振動的基礎上開展雙臺虛擬振動和多維虛擬振動。

2）虛擬振動還有很多局限，實物振動試驗中，裝備在振動載荷下，其動力學特性普遍存在變化，頻響函數是實時變化的，但目前基于有限元方法獲取頻響函數不能實時變化，虛擬振動試驗還和實物振動試驗有差異，虛擬振動試驗不能替代實物振動試驗。可開展基于數字孿生的虛擬振動試驗技術研究，根據實測試驗數據，對有限元模型進行實時修正。

3）基于有限元模型開展的虛擬振動在低頻段相對準確，結合產品經歷振動環境的頻段，高頻段可結合統計能量法開展相關的研究。