汽車前縱梁結構耐撞性分析及多目標優(yōu)化設計

汪 婷，李翼良，張代勝，谷先廣*

（1.合肥工業(yè)大學 智能制造技術研究院，安徽 合肥 230009；2.合肥工業(yè)大學 汽車與交通工程學院，安徽 合肥 230009）

前縱梁是汽車前端結構的重要組成部分之一，不僅要作為承重結構，還要作為汽車發(fā)生前部碰撞時的主要吸能結構。根據汽車在發(fā)生碰撞時撞擊位置的不同，可以將碰撞劃分為前部碰撞、側面碰撞和尾部碰撞三種類型。在這三種類型中，前部碰撞最為常見且碰撞工況較為復雜，其中包含正面100%、正面40%和其他小角度偏置碰撞，且正面40%偏置碰撞涵蓋了汽車在正常行駛中與對向車輛發(fā)生碰撞的情況，而絕大多數正面碰撞都具有不同的百分比重疊碰撞[1]。在汽車發(fā)生前部碰撞時，前縱梁約能吸收60%的沖擊能量[2]，在保障乘員安全方面發(fā)揮著不可替代的作用。

近年來，大量學者對前縱梁的耐撞性和吸能性進行了研究。例如：劉珊[3]基于100%剛性壁障碰撞和正面40%可變形壁障碰撞兩種工況對具有誘導結構的前縱梁和不帶誘導槽的前縱梁做了對比研究，結果表明帶有誘導結構的縱梁可以產生穩(wěn)定的外延變形模式，且提高了整車的耐撞性。陳吉清[4]等人通過研究材料厚度、結構的截面尺寸以及結構間的連接方式對前縱梁在受到沖擊載荷下耐撞性的影響。

綜上所述，前縱梁作為汽車發(fā)生正面碰撞時主要的吸能部件，其性能的好壞關系著車內乘員的生命安全，因此，本文系統(tǒng)的將試驗設計、代理模型技術、多目標優(yōu)化理論及可靠性優(yōu)化方法應用于前縱梁，在提高結構耐撞性的同時兼顧其輕量化。

1 模型建立與驗證

1.1 前縱梁有限元模型建立

前縱梁在軸向方向受到的動態(tài)沖擊工況的模擬在有限元軟件ABAQUS 中進行。仿真采用四節(jié)點的殼單元網格，其尺寸設置為5 mm，同時為防止沙漏出現(xiàn)，在殼單元厚度方向上設置五個積分點。根據動態(tài)落錘沖擊試驗，約束前縱梁仿真模型底端每個節(jié)點的六個自由度，落錘沖頭簡化為一塊同樣質量的剛性板，并賦予剛性質量板向下壓的初速度（12.5 m/s）。模型中不考慮焊點失效的情況，所以采用剛性連接方式模擬前縱梁里面的焊點單元。整個有限元模型包含33 225 個節(jié)點，31 936 個殼單元，總質量為5.38 kg，整體采用通用接觸，接觸時的摩擦系數定義為0.15。邊界條件只定義軸向壓潰方向上的自由度，其余自由度全部固定。有限元模型的材料的密度為7 850 kg/m3，泊松比為0.33，彈性模量為210 GPa，材料塑性段力學響應由CA340/590DP、B280VK、SPHC 和DC03 這四種材料準靜態(tài)和高速拉伸試驗所獲得的J-C 金屬本構模型[5]來描述，由準靜態(tài)得到的材料參數如表1 所示，真實應力應變曲線圖如圖1所示。有限元模型如圖2 所示。

圖1 真實應力應變曲線

圖2 前縱梁有限元模型

表1 前縱梁材料基本參數

1.2 有限元模型驗證

將建立好的有限元模型提交計算后查看計算結果，總能量為17 160 kJ，沙漏能為56.6 kJ，占據總能量的0.33%，滿足要求。結構的初始峰值力為289 kN，壓縮距離為203 mm。對長為1 120 mm的前縱梁進行動態(tài)落錘沖擊試驗，最后整個前縱梁只有三個焊點發(fā)生失效，其余變形均屬正常，壓縮距離為256 mm，剩余144 mm 的部位沒有產生形變。為了驗證有限元模型的準確性，首先需要將有限元模型的變形模式與結構的實際變形模式進行對比，其變形圖如圖3 所示。從圖3 可以清晰的看出，結構基本上的變形模式是屬于漸進式壓潰，曲面的引入并沒對結構的變形造成很大的影響，且兩者的變形模式幾乎相同，由此可以初步判定有限元模型的準確性。

圖3 前縱梁仿真與試驗對比圖

在比較完結構的變形模式之后，還需比較有限元仿真模型與實際試驗在沖擊力方面的差別，從這兩方面來驗證有限元模型的有效性。圖4 為結構在動態(tài)沖擊工況下的力-位移曲線圖。從試驗曲線與仿真曲線的走勢來看，兩者基本相同。

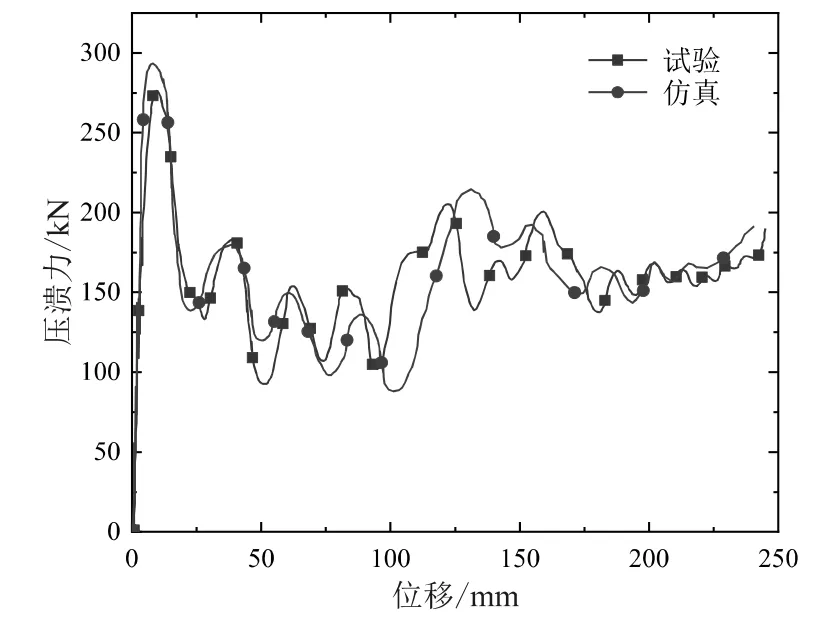
圖4 前縱梁壓潰力位移曲線圖

通過結構的變形模式與壓潰力-位移曲線兩者基本上可以確定前縱梁仿真模型具有較高精度，因此，前縱梁結構的有限元建模方法可以應用到后文中的優(yōu)化設計部分。

2 優(yōu)化設計

在前面的模型建立與驗證中，前縱梁結構中主要變形的部分其材料強度均參差不齊，其中CA340/590DP 和DC03 兩者的屈服強度差距更是不止一倍，由于CA340/590DP 材料的屈服強度與抗拉強度均高，因此，將前縱梁材料全部替換為CA340/590DP，為了進一步提高前縱梁結構的耐撞性，將對前縱梁的結構進行多目標優(yōu)化，其目標是將質量減輕量和比吸能提高5%以上。優(yōu)化設計主要包括有限元模型的建立和驗證、優(yōu)化問題定義、試驗設計、代理模型建立、確定性優(yōu)化設計、可靠性優(yōu)化設計和優(yōu)化結果驗證。

2.1 多目標優(yōu)化問題定義

前縱梁的優(yōu)化主要目的在于提高其耐撞性和減輕質量。因此，以前縱梁比吸能（Specific Energy Absorption, SEA）和質量M 作為設計目標；以前縱梁結構的平均壓潰力（Mean Crushing Force,MCF）以及其初始峰值力（Initial Peak Crushing Force, IPCF）為設計約束；以發(fā)動機艙邊梁及其外板、內部兩塊加強板的厚度以及外板加強板的高度作為設計變量。目標函數與約束條件初始響應如表2 所示，設計變量示意圖如圖5 所示，各設計變量的初始取值及變化范圍如表3 所示。

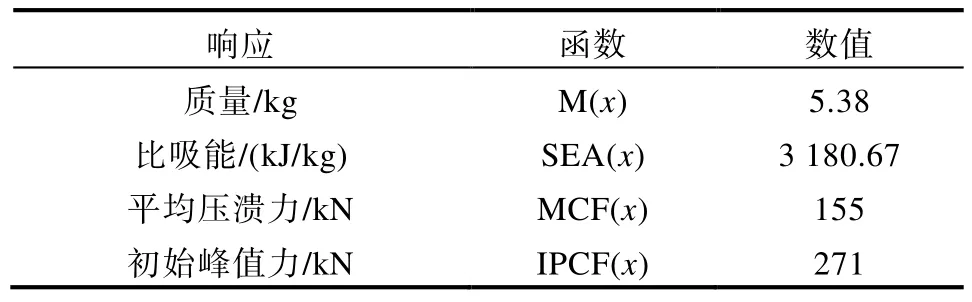
表2 目標函數與約束條件初始響應

圖5 設計變量示意圖

表3 設計變量初始取值及變化范圍

2.2 試驗設計與近似模型搭建

試驗設計與代理模型相結合的數學預測方法，能夠有效降低計算成本，提高優(yōu)化效率，目前已被廣泛應用于汽車工程研究領域。本文采用優(yōu)化拉丁超立方試驗設計（Optimal Latin Hypercube Design, OLHD）[6]，在有限的設計空間內生成50 組樣本點用以構建近似模型。為驗證代理模型的精度，還需要另外生成20 組樣本數據。再利用有限元分析軟件計算各樣本點處的響應值，完成樣本數據的構建。

本文基于實驗設計樣本數據，采用支持向量機回歸（Support Vector Regression, SVR）近似模型[7-8]來代替有限元模型，針對質量響應與設計變量之間的線性關系可以選用線性的核函數來搭建近似模型；而比吸能響應與設計變量之間為非線性關系，則需要采用非線性的核函數搭建近似模型，常見的核函數如表4 所示。

表4 支持向量回歸模型核函數類型

常用的代理模型精度評估參數有確定性系數（Coefficient of Determination）R2、最大相對誤差（Maximum Relative Error）max(RE)，表達式為

式中，yi為有限元仿真值；為近似模型響應值；為有限元仿真的平均值；n為采樣點數量。

線性核函數的基本參數設置以及近似模型精度驗證如表5 所示。在非線性的核函數中，本文需要采用粒子群優(yōu)化（Particle Swarm Optimization,PSO）算法[9]對SVR 近似模型中的懲罰系數C、不敏感系數ε以及核函數參數進行優(yōu)化，以構建出精度較高的PSO-SVR 近似模型。優(yōu)化后的核函數參數如表6 所示。

表5 線性核函數參數設置

表6 非線性核函數參數設置

前縱梁結構PSO-SVR 近似模型的精度驗證指標如表7 所示，所有響應的確定性系數R2都大于0.9 且最大相對誤差max(RE)值都小于0.1，達到了近似模型的精度要求，可用于后續(xù)優(yōu)化。

表7 PSO-SVR 近似模型精度指標

2.3 確定性優(yōu)化設計

依據上文中對優(yōu)化問題的定義，對前縱梁結構進行多目標優(yōu)化設計，確定性優(yōu)化設計的數學表達式如下：

為了兼顧前縱梁結構的耐撞性和輕量化兩個目標，本文采用多目標優(yōu)化算法非支配排序遺傳算法Ⅱ（Non-dominated Sorting Genetic AlgorithmⅡ, NSGA-Ⅱ）[10]在給定的設計變量取值范圍內進行全局尋優(yōu)，尋找出各個設計變量最佳值。經過NSGA-Ⅱ算法對上文搭建的PSO-SVR 近似模型的700 次左右的迭代尋優(yōu)，最終得到了確定性優(yōu)化設計的解集，通過最小距離選解法，得到最優(yōu)設計變量取值，如表8 所示，其目標的優(yōu)化結果如表9 所示。

表8 設計變量取值對比

表9 確定性優(yōu)化設計結果分析

從表9 可以看出，確定性優(yōu)化設計的結果相比較于原始結構設計有著一定的提升，在質量方面，減重達到了3.4%，比吸能方面也有著9.1%的改善，所以在前縱梁結構與材料重新設計與選用之后，對結構耐撞性有著明顯的改善作用。

2.4 可靠性優(yōu)化設計

通過確定性優(yōu)化設計，前縱梁結構的耐撞性以及輕量化都得到了明顯的改善，但是在實際設計過程中，會存在很多不可控因素，例如加工精度、裝配誤差等等，導致確定性優(yōu)化設計結果不滿足要求。因此，本節(jié)在確定性優(yōu)化的基礎上開展結構的可靠性優(yōu)化設計。

在進行可靠性優(yōu)化設計時，本文采用正態(tài)分布來描述設計變量的不確定性，變異系數設置為0.05，并采用蒙特卡羅模擬方法對設計變量的確定性優(yōu)化解進行可靠度評估，因此，需要基于描述性抽樣法在設計空間內采集10 000 個樣本點，將新采集樣本點通過前文所搭建的PSO-SVR 高精度近似模型求解其輸出響應，并計算其可靠度。確定性優(yōu)化設計最優(yōu)解中約束條件的可靠度值如表10 所示。

表10 確定性優(yōu)化解的可靠性評估

基于確定性優(yōu)化設計解，本文可靠性指標為95%的前縱梁優(yōu)化設計的數學模型可表示為

式中，μ為目標函數M(x)與SEA(x)兩個目標函數響應的均值；P為平均壓潰力小于155 kN 時的概率，對于初始峰值力設置的概率同平均壓潰力一樣。

可靠性優(yōu)化設計與確定性優(yōu)化設計基本相同，都是需要通過運用PSO-SVR 近似模型以及NSGA-Ⅱ優(yōu)化算法經過多次的迭代求解，最終獲得滿足約束條件的最優(yōu)解。表11 為前縱梁結構可靠性優(yōu)化設計的設計變量取值結果。

表11 可靠性優(yōu)化設計的設計變量取值

優(yōu)化設計的結果是根據近似模型預測所得到，所以還需要通過有限元模型進行驗證其響應是否準確，表12 為可靠性優(yōu)化設計與有限元仿真結果的誤差對比，由表可知，近似模型的優(yōu)化值與仿真值之間的各項誤差均小于4%，因此，可以證明優(yōu)化結果具有較高的準確性。

表12 可靠性優(yōu)化設計與有限元仿真結果誤差對比

為了清晰對比前縱梁原始結構、確定性優(yōu)化設計與可靠性優(yōu)化設計的耐撞性分析，表13 展示了不同設計方案的優(yōu)化結果對比，圖6 展示了不同設計方案下的壓潰力位移曲線圖。

表13 不同設計方案的優(yōu)化結果對比

從表13 和圖6 可以看出，相比于原始結構，確定性優(yōu)化設計與可靠性優(yōu)化設計在質量響應與比吸能響應方面均有提升，峰值壓潰力也都比初始結構低，雖然可靠性優(yōu)化設計中的比吸能要低于確定性優(yōu)化設計，但可以明顯地看出可靠性的峰值壓潰力比確定性要低，說明可靠性優(yōu)化的結構在壓潰時比較穩(wěn)定，在前縱梁的實際應用中，可靠性優(yōu)化設計更具有實際工程價值。

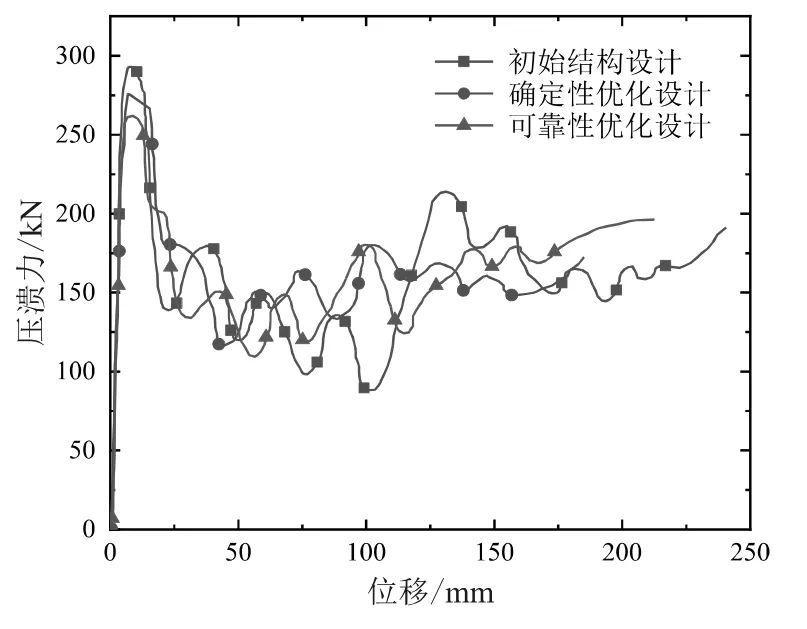
圖6 壓潰力位移對比曲線圖

3 總結

1）本文建立了前縱梁結構的有限元模型，并基于動態(tài)落錘試沖擊試驗驗證了有限元模型的準確性和建模方法的可靠性。

2）本文對前縱梁結構進行了多目標優(yōu)化設計，通過優(yōu)化拉丁超立方試驗設計生成樣本空間，并通過PSO-SVR 近似模型對前縱梁結構開展確定性優(yōu)化設計與可靠性優(yōu)化設計。

3）優(yōu)化結果表明，優(yōu)化的前縱梁質量減輕了5.5%，比吸能提高了了6.2%，都達到了質量減輕量和比吸能量提高量均為5%的優(yōu)化目標。在實現(xiàn)輕量化的同時，前縱梁的耐撞性也得到了提升。