代理模型技術在船舶結構優化設計的應用

周廣群

（濟寧市港航事業發展中心，山東 濟寧 272004）

隨著技術的進步和產品的不斷升級換代，對船舶的性能提出了越來越高的要求，船舶結構的高可靠性和穩健性是未來的發展方向[1,2]。所以，船舶的制造企業必須秉承不斷創新的發展理念，采用新技術促進船舶制造技術的進行，尤其在船舶結構設計方面，促進結構的合理升級，在保證結構強度等性能指標的情況下減少質量，提高船舶制造效率[3]。

在對船舶的優化研究方面，文獻[4]采用代理模型和遺傳算法對船舶框架結構進行了輔助優化設計，取得了良好的應用價值。文獻[5]調用代理模型代替板架有限元仿真模型的方法對船體結構子系統進行迭代計算，獲得最佳的設計方案。文獻[6]采用Kriging 模型對船舶板架強度和穩定性計算的適用性研究，模型精度滿足船舶的工程精度要求。文獻[7]采用Kriging 代理模型，對船舶興波阻力、垂蕩和縱搖運動幅值進行了多目標優化，取得了好的優化效果。基于Kriging 模型，文獻[8]對船舶底板架強度和穩定性繼續了全局敏感度分析，得到了敏感度分析結果。

本文闡述了基于代理模型的船舶結構的優化設計思路框架，并探討了常用的技術，包括樣本點試驗設計、代理模型技術和智能尋優技術。

1 船舶總體結構設計

在進行船舶的總體結構設計時，首先要進行總體的方案設計，主要包括：分析同類型船的資料，確定各個設計參數可能的選擇范圍，設立一個初步的新船總體設計方案；估算并分析新船的主要技術和經濟指標，考慮并解決可能存在的主要矛盾。

在船型特征和總體布置構思時，考慮如下的內容：主船體特征、機艙位置、甲板層數、貨艙形式、上層建筑的大小和位置和船體結構特點。

船舶設計時涉及的變量參數多，且信號源不統一，如聲信號、振動信號及光信號等變量的綜合優化，這牽涉到多學科知識的交叉耦合融合研究。在這種情況下，需要進行多物理場的耦合仿真計算，以得到多信號變量下的響應參數，現代多物理場耦合計算軟件Ansys 能完成仿真計算工作，但是，計算過程漫長，每一次迭代運行可能要幾小時甚至幾十個小時，而智能優化過程往往迭代計算上百次以上才能得到全局最優解，如果每次的迭代響應值都由軟件仿真計算完成，那么總體的優化計算時間是冗長而無法忍受的，代理模型的運用很好的解決了計算時間問題，以滿足精度要求的代理模型替代軟件仿真計算，這就能夠極大的節省仿真時間而使優化過程順利進行，特別是像船舶結構的大型仿真優化計算，不借助于代理模型幾乎是無法完成的。

2 船舶結構的代理模型技術框架

船舶結構的技術框架如圖1所示。通用的代理模型即利用代理方法對離散的數據進行擬合的數學模型。而實際的船舶結構的實際物理模型往往非常復雜，多物理場下設計變量與目標響應間不具有顯式的函數關系式而表現為多參數非線性。所以在優化算法中，用滿足精度要求的代理模型代替多物理場仿真模型，具體包括船舶結構參數的選取、樣本點配置和高精度代理模型構建。

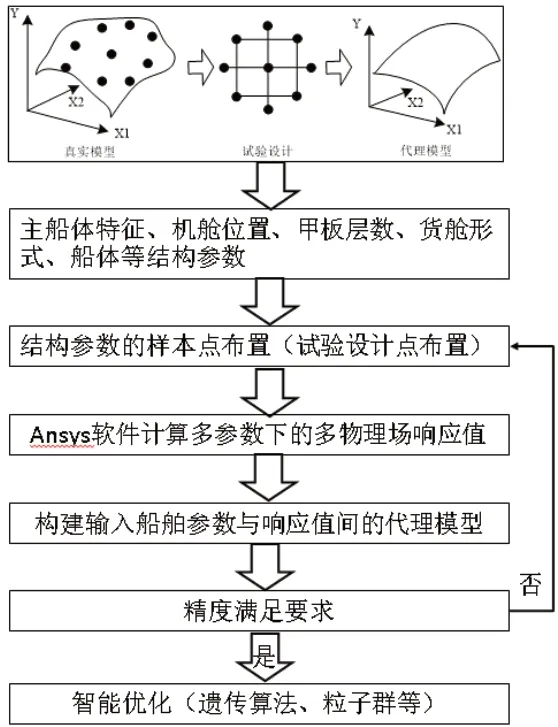
圖1 船舶的代理模型優化技術框架

船舶結構的代理模型構建包括樣本點配置、代理模型的函數擬合、代理模型精度的評價，具體步驟如下：

（1）選取船舶的結構參數，設定其取值范圍，采用試驗設計方法在參數范圍內生成若干樣本點；

（2）通過Ansys 仿真軟件獲得與輸入數據參量相對應模型下的輸出響應參數；

（3）根據代理模型理論構建上述船舶輸入結構參數與輸出響應間的擬合模型，即建立輸入與輸出變量間的擬合代理模型；

（4）代理模型的誤差精度分析，當達到精度要求的代理模型可以代理仿真模型進行優化迭代計算，否則，通過增加樣本點對代理模型改進直至滿足精度要求。

3 船舶的優化相關技術

代理模型主要包含兩方面的內容，其一是構造模型的樣本點如何選取，屬于試驗設計的范圍，主要包括全因子試驗設計、正交試驗設計、拉丁超立方試驗、均勻試驗設計等；其二是數據擬合與預測模型的建模，這是代理模型的主體，主要包括神經網絡、徑向基模型、Kriging 代理模型等。

3.1 試驗設計方法

試驗設計的作用是合理且有規劃的構建采樣點，其實質上是挑選有代表性的試驗點，其指導原則是均勻分散，且使試驗點均勻的散布于整個試驗空間內，另外要整齊可比，便于試驗結果的分析。試驗設計方法為代理模型的搭建提供了有代表性的樣本點。常用的試驗設計方法有：全因子試驗設計、正交試驗設計、拉丁超立方試驗設計和均勻試驗設計等。

3.1.1 全因子試驗設計

全因子試驗設計是對設計變量的各因子與各水平間的所有組合安排試驗。比如，當優化變量為n，且每個變量分別取p 個不同的水平值時，采用全因子試驗的次數為pn，當優化變量和水平數目比較大時，這種方法的試驗次數非常大。所以在實際的試驗方案設計中一般不采用這種方法，而全因子試驗設計僅僅用于優化變量和水平數都比較少的場合，其優點是能夠比較全面的分析優化變量的交互性對響應結果的影響。

3.1.2 正交試驗設計

正交試驗設計方法是根據“整齊可比且均勻分散”的思路提出的。并采用正交表安排試驗，此方法的最大優點是能用較少的試驗次數來大體上反映出全部試驗數據的最大信息。并通過對試驗結果的方差分析得出對試驗結果影響最大的設計參量。

在數學上，如果兩個向量的內積之和等于零，則稱這兩個向量正交，而正交試驗設計的“正交”是從空間幾何中向量正交的定義引申而來的。而其它試驗設計方法如均勻設計、因子設計等都包含著正交的思想。在正交試驗設計中，主要用到正交表，其中，正交表的符號表示為，式中t 為試驗次數；n 為水平數；q 為因子數。

3.1.3 拉丁超立方試驗

1979年， 拉丁超立方抽樣（Latin Hypercube Sampling，LHS）由Mckay 等人提出。其主要用于計算機仿真試驗，能夠使樣本點均勻的散布于較大的設計空間，拉丁超立方試驗設計的原理如下：

假設優化問題中有n 個優化設計變量，且各變量有q 個水平值，則拉丁方表為q×n 階矩陣，拉丁方設計表中，n 為設計變量個數；q 為變量的水平數目。具體設計步驟如下：確定試驗次數q；把每個優化設計變量的水平取值的區間劃分成q 組（即q 個水平），且使每組選取到的概率為1/q；在上述劃分的子區間中，采用隨機數的方式選取；重復操作上述步驟。

拉丁超立方試驗設計采用數學表示為：

3.1.4 均勻設計方法

均勻設計方法是由我國方開泰和王元兩位數學家在1978年創立的，此法主要是從均勻性角度考慮的試驗設計法。

試驗設計中每個設計變量的每個水平選取一次，這也是均勻試驗設計的最主要的特點，所以試驗次數相對較少。而當設計變量多且每個變量的水平數較多時，為了減少試驗次數以節約成本，可以采用均勻設計。

其它試驗設計方法有，響應曲面設計類型的中心組合設計、基于回歸模型的最優設計和最大化熵設計等。

3.2 代理模型技術

3.2.1 神經網絡模型

人工神經網絡主要是通過模仿動物神經系統研究得出的。1943年，數理學家Pitts 和心理學家Mcculloch提出了神經元的數學模型，這種模型是在分析和總結神經元特性基礎上歸納出來的。

按照神經網絡之間連接方式的不同，神經網絡可分為前向（Feedforward）、反饋（Back Propagation）與自組織神經網絡（Self-organizing Neural Network）。其中，反饋神經網絡（Back Propagation Neural Networks，BPNN）在工程優化中應用比較廣泛，BPNN 也就是通常所說的BP 神經網絡，在工程上運用最廣泛的是三層前向BP 神經網絡，該網絡由輸入層（Input layer）、隱含層（Hidden Layer）及輸出層（Output Layer）所組成，其結構網絡如圖2所示。

圖2 三層前向神經網絡示意圖

3.2.2 徑向基代理模型

1985年，多維空間插值技術-徑向基函數模型由Powell 提出，徑向基函數模型是通過對徑向函數的線性加權計算來構造出來的。徑向基函數是樣本點與預測點間的歐氏距離來定義的單調函數，其優點是通過歐式距離，把多維復雜問題轉變為相對簡單的一維歐式距離問題，徑向基函數的數學表達式如下：

式中，wi為權重系數；為徑向基函數；為樣本點與預測點間的歐氏距離。

3.2.3 Kriging 代理模型

1951年，Kriging 近似法由南非地質學者Krige 首先提出，主要用于礦產儲量的部分探測，Kriging 法主要是采用方差的變化來表示空間的變化，并能保證預測值的誤差最小。

Kriging 代理模型是基于統計理論的方差最小無偏估計模型，響應值與自變量之間的關系表示為：

另外，支持向量機、隨機森林等模型也常用于代理模型的構建。

3.3 智能尋優技術

3.3.1 遺傳算法

遺傳算法是根據大自然中生物體進化規律而設計，根據遺傳、選擇、交叉和變異操作，使適應度強的個體得以保存和繁衍，進而達到尋優的目的。

遺傳算法已被人們廣泛地應用于各類優化問題以及機器學習、信號處理等領域。

3.3.2 粒子群優化算法

PSO 算法的實質是粒子在空間中不停做有方向的變速運動，通過自身的記憶和群體的交流來找到下一個位置，從而尋找最優解。速度和位置的更新公式為：

以船舶結構輸入和響應構建的代理模型導入到智能算法中，并作為適應度函數進行尋優，進而達到優化船舶結構的目的。

4 結論

論文分析了船舶的總體結構設計方案，探討了船舶結構的代理模型技術框架，在此基礎上闡述了船舶結構設計的代理模型技術，包括樣本點設計、代理模型構建和智能尋優技術，這對船舶結構的多參數設計提供了有益的參考和思路。