快堆堆芯單排組件抗震計算關鍵算法研究與驗證

周世安,黑寶平,高付海

(中國原子能科學研究院,北京 102413)

對于反應堆及核設施,在強烈的外部載荷如地震作用下確保安全運行是最基本的要求之一。液態金屬快堆(LMFR)中包含低壓運行的系統以及薄壁柔性組件,這使其在地震作用下受到的影響極其顯著。對于快堆堆芯,其地震下的運動主體十分龐大,全堆芯的六角形套管組件多達成百上千根,每根組件與相鄰的6根組件均可能發生碰撞,且每時每刻的運動狀態都在發生變化,從而導致碰撞的部位也隨之變化,同時會受到液體金屬冷卻劑與組件流固耦合的影響,這使得堆芯抗震問題變得尤為復雜,因此建立針對快堆堆芯的抗震分析方法很有必要。

快堆堆芯的抗震分析方法通常分為設計試驗和程序分析,試驗數據直觀可靠,但開展全堆芯組件抗震試驗成本高昂,相比之下,研發專用程序以準確高效地進行全堆芯抗震計算和評價是一種經濟可行的方式。國外許多國家已研發出了成熟的快堆堆芯抗震分析軟件[1-5],有的軟件是專用于堆芯抗震的計算程序,如日本研發的FINAS及REVIAN-3D、印度研發的CORE-SEIS、韓國研發的SAC-CORE和意大利研發的CORALIE及CLASH;有的則是在原有的通用成熟軟件中進行了更新,使其具備快堆堆芯抗震計算能力,如法國的CASTEM,美國的COSMOS,俄羅斯的DINARA以及日本的FINDS、SAFA和SALCON。

程序設計采用的計算方法通常分為2種:模態疊加法和直接積分法。模態疊加法可提升計算速度,但忽略了高階模態的影響;直接積分法則計算速度較慢。使用模態疊加法的程序有COSMOS、FINDS和SAFA等,SAFA還配置了專用于單自由度系統的Nigam時間積分法,更大程度地提高了計算效率。使用直接積分法的程序有CORE-SEIS、SACCORE、FINAS和SALCON等,SALCON在直接積分法的基礎上采用GUYAN自由度凝聚方法減少矩陣維度,并通過變時間步長進一步提升計算效率。程序中堆芯組件管腳約束方式通常有3種:固支約束+等效彈簧、簡支約束+間隙彈簧,以及固支約束+等效旋轉彈簧元。大多數程序都可對管腳底端施加固支或簡支約束,并在管腳球形密封處添加等效彈簧以施加間隙等效剛度,而FINDS與FINAS除對底端施加固支約束或簡支約束外,還能使用旋轉彈簧元來模擬管腳處的運動。碰撞動力方程的常用求解方法有中心差分法、Newmark法和基于Newmark法衍生的Wilson-θ法,其中Newmark法的參數γ和β變化時,算法的顯隱式、計算速度和穩定性條件隨之改變。本程序取γ=1/2、β=1/4,使Newmark法為平均加速度法,這種參數取法使算法為隱式且無條件穩定,通過這種取法保證求解的穩定性。冷卻劑與堆芯組件的流固耦合計算方式有3種:集中附加質量法、均質化方法[6]和有限元計算法[5,7]。大部分程序常用集中附加質量法,該方法可調整組件的1階固有頻率以體現冷卻劑對組件的附加作用。

中國原子能科學研究院曾使用ANSYS、FINAS以及CASTEM對快堆堆芯組件進行了初步的單根[8]以及單排組件抗震分析計算[9],但一直沒有形成自主開發的堆芯抗震分析專用軟件程序。

針對我國在快堆堆芯抗震計算自研專用程序方面的空白,本文研究建立適用于大規模快堆堆芯抗震分析的理論模型,研發能解決地震載荷作用下堆芯組件復雜非線性多點碰撞問題的時間歷程關鍵算法,并從簡單的懸臂梁振動理論解到國際原子能機構(IAEA)組織的法國RAPSODIE堆單排19根組件試驗結果進行從下到上的逐步驗證,完成單排組件情況下地震分析理論的建立與驗證,證明算法的正確性和可行性,為后續多排組件乃至全堆芯抗震分析奠定基礎。

1 理論模型

快堆堆芯組件在地震動時的動力學方程為:

(1)

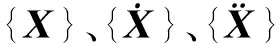
鑒于組件在地震過程中主要表現的行為是水平碰撞且在碰撞中基本沒有軸向變形和剪切變形,故將組件簡化為歐拉梁,并以此為根據構建初始的質量矩陣與剛度矩陣。

1.1 質量矩陣和剛度矩陣

僅考慮兩端受載的情況,則歐拉梁的梁平衡方程為:

(2)

其中:u為梁的撓度,即梁單元節點處垂直于軸線方向的位移;E為梁的彈性模量;I為梁的慣性矩。

通過Hermite插值方程表示的梁形函數與虛位移原理,可推導出梁的單元剛度矩陣和單元質量矩陣,通過對不同參數梁的單元矩陣進行裝配最終獲得總的質量矩陣和剛度矩陣。為保證計算精度足夠高并大幅提升計算效率,本文采用GUYAN縮減法[10]進行相應的自由度縮減。首先需要選定主從自由度,其中主自由度是施加了力、計算邊界條件和需要輸出結果的所在自由度,其余的則是從自由度。本質上,縮減矩陣是使用主自由度來表示從自由度。對于包含阻尼和外力作用的系統,其動力學方程為:

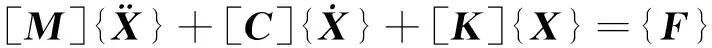
(3)

其中,{F}為受到的外力向量。

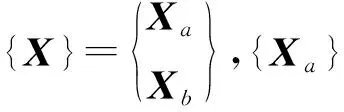
(4)

根據靜平衡近似,可得到:

(5)

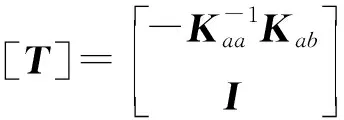
[K][T]{Xb}={F}

(6)

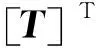
(7)

(8)

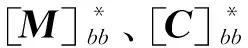
1.2 結構阻尼矩陣

對于地震作用下的堆芯組件,除流固耦合產生的附加阻尼及碰撞時產生的碰撞阻尼,組件結構本身存在結構阻尼,工程上常用Rayleigh阻尼[11]來表示。Rayleigh阻尼可表示為:

[C]=a0[M]+a1[K]

(9)

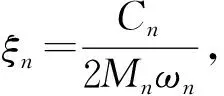
(10)

對于新型結構,通常情況下需通過試驗測量獲取各階精確阻尼比和頻率。快堆堆芯組件材料一般為不銹鋼,但燃料組件和屏蔽組件內部結構材料和工藝設計有所差異,因此二者阻尼比不同。由于快堆堆芯組件為細長梁結構,第1階和第2階振型對相鄰組件的碰撞行為起主要作用,故在求解堆芯抗震總動力方程的結構阻尼矩陣時,分別選取對應上述振型的第1階和第2階固有頻率和阻尼比。在確定ω1和ω2及ξ1和ξ2的基礎上,若ξ1=ξ2=ξ,則a0和a1可表示為:

(11)

1.3 碰撞剛度及阻尼

通常情況下,快堆堆芯組件的碰撞剛度可通過以下兩種方法獲取:1) 直接法,通過對真實組件進行碰撞試驗直接獲取程序所需碰撞剛度;2) 間接法,通過組件壁面的擠壓剛度間接計算求得程序所需碰撞剛度。本文采用間接法計算碰撞剛度Kgap,可通過式(12)求得[1]。

(12)

其中,Ket1和Ket2分別為發生碰撞的兩根組件的擠壓剛度。

擠壓剛度可通過對組件施加如圖1所示的壓力使其發生形變來求得。通過有限元對組件進行建模,兩端施加力F,計算出ΔD,便可求出組件的擠壓剛度Ket:

(13)

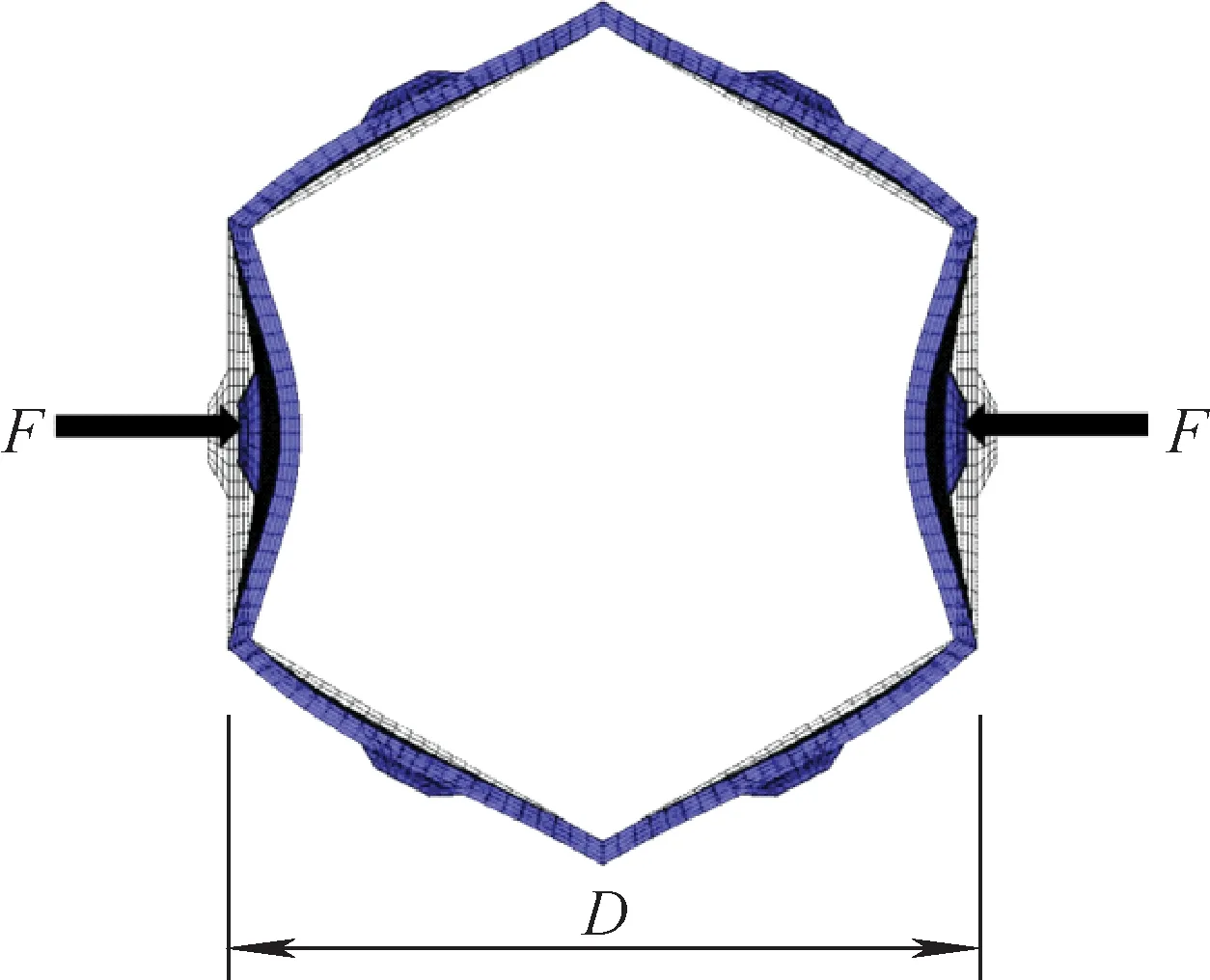
圖1 擠壓剛度計算示意圖Fig.1 Schematic diagram of extrusion stiffness calculation

當發生碰撞的兩根組件的結構材料和截面形狀一致時,Ket1=Ket2=Ket。根據碰撞剛度Kgap計算得到沖擊阻尼Cgap:

(14)

其中,e為材料的彈性系數,對于不銹鋼,e一般為0.55。

在單排組件的情況下,組件墊塊處節點的位移無需根據幾何位置關系進行分解,此時剛度的設置得到相應的簡化。當第j根組件受到前后兩根組件的沖擊時,總剛度矩陣和阻尼矩陣變為如下形式:

(15)

aj-1=cj-1+Pgap

(16)

bj-1=-Pgap

(17)

其中:c為原始總剛度矩陣和阻尼矩陣在碰撞組件處的對應項;Pgap為碰撞產生的沖擊剛度或沖擊阻尼;a為碰撞對剛度矩陣和阻尼矩陣在對角項上產生的影響;b為碰撞對剛度矩陣和阻尼矩陣在非對角項上產生的影響。

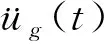
2 基準例題驗證

2.1 等截面懸臂梁固有頻率驗證

對于簡單的等截面懸臂梁(圖2),其存在固有頻率理論解。將梁截面參數輸入到研發的自研程序內,計算固有頻率并與理論解進行對比,以驗證梁單元的構建與裝配,以及自由度縮減法則的正確性。

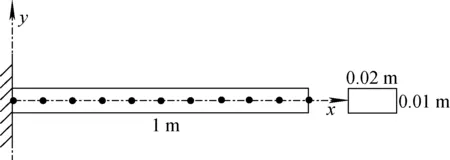
圖2 簡單等截面懸臂梁示意圖Fig.2 Simple uniform cantilever beam

圖2所示等截面矩形梁,長為0.02 m、寬為0.01 m、高為1 m。其楊氏模量為2.1×105MPa、密度為7.85×103kg/m3、泊松比為0.3。將該梁分別在ANSYS與自研程序中建模并與理論解進行對比,結果列于表1。對比發現:自研程序計算的前3階固有頻率與理論解和ANSYS的計算結果完全吻合,隨著階數的升高,誤差逐漸變大,在前5階,頻率相對誤差均小于1%。

2.2 中國實驗快堆堆芯燃料組件固有頻率驗證

真實組件管腳和柵板插座為間隙配合裝配。對中國實驗快堆(CEFR)堆芯燃料組件進行質量等效與剛度等效,等效參數列于表2。

表1 簡單等截面懸臂梁固有頻率計算結果對比Table 1 Comparison between theoretical and calculation results of nature frequency in simple uniform cantilever beam example

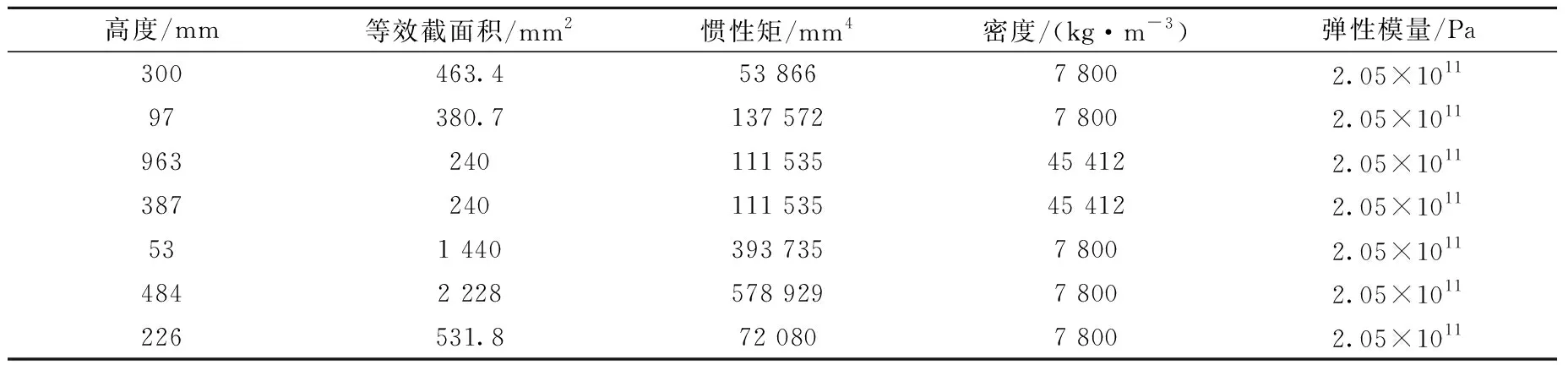
表2 CEFR堆芯燃料組件等效后的梁參數Table 2 CEFR core fuel assembly equivalent beam parameter

組件可等效為變截面梁,在管腳底端設置為簡支約束,且在管腳球形密封處設置剛度為8.8×105N·m的等效彈簧[12],將模型參數輸入自研程序和ANSYS中計算固有頻率并進行對比,結果列于表3。從表3可知,二者吻合較好,最大誤差在第3階處,僅為0.49%。2.1和2.2節中梁的約束條件不同、截面參數不同,因此梁單元的構建和矩陣自由度縮減方式均不同,通過這兩個案例可驗證組件等效方法的合理性,同時也可驗證程序梁單元構建以及GUYAN縮減法的正確性。

表3 CEFR堆芯燃料組件ANSYS與自研程序固有頻率計算結果對比Table 3 Comparison between nature frequenciesin CEFR core fuel assembly by ANSYS and code

2.3 CEFR單根組件空氣中時程分析驗證

在堆芯組件大規模非線性碰撞情況下,ANSYS計算精度低且計算時間長,但單根組件不存在碰撞時其計算結果是具有可信度的。通過單根組件在自研程序和ANSYS中計算結果的對比,可驗證時程分析法的正確性。

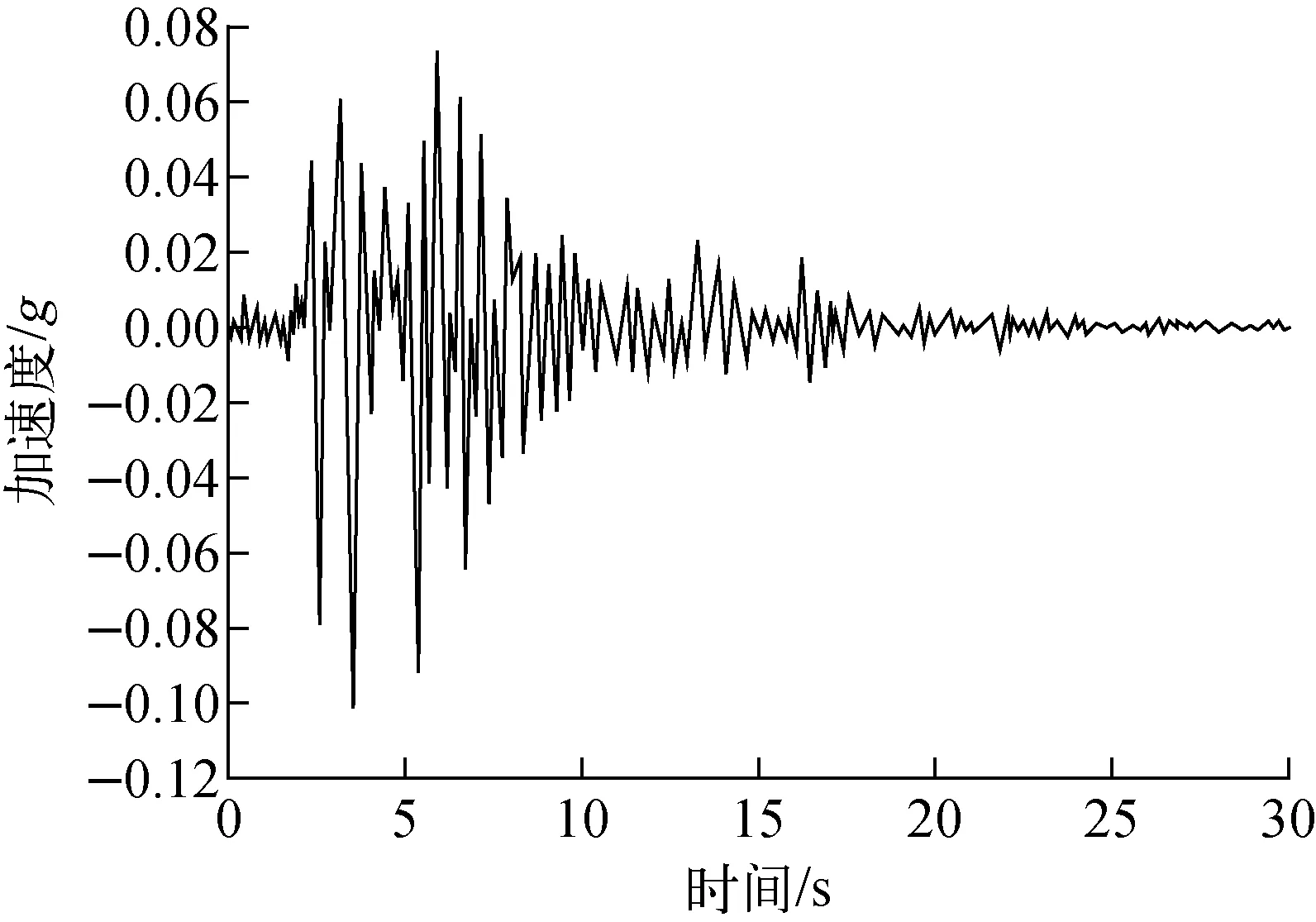
圖3 KOBE波地震輸入Fig.3 Kobe earthquake seismic input

針對2.2節中提到的CEFR燃料組件模型,采用ANSYS和自研程序分別進行時程分析計算,其中KOBE波地震輸入如圖3所示,計算結果對比如圖4所示。由圖4可知,二者基本吻合,其中ANSYS計算的組件頂點處位移最大值為5.263×10-4m,自研程序計算的組件頂點處位移最大值為5.320×10-4m,二者相對誤差為1.08%,由此證明單組件的時程分析法是正確的。

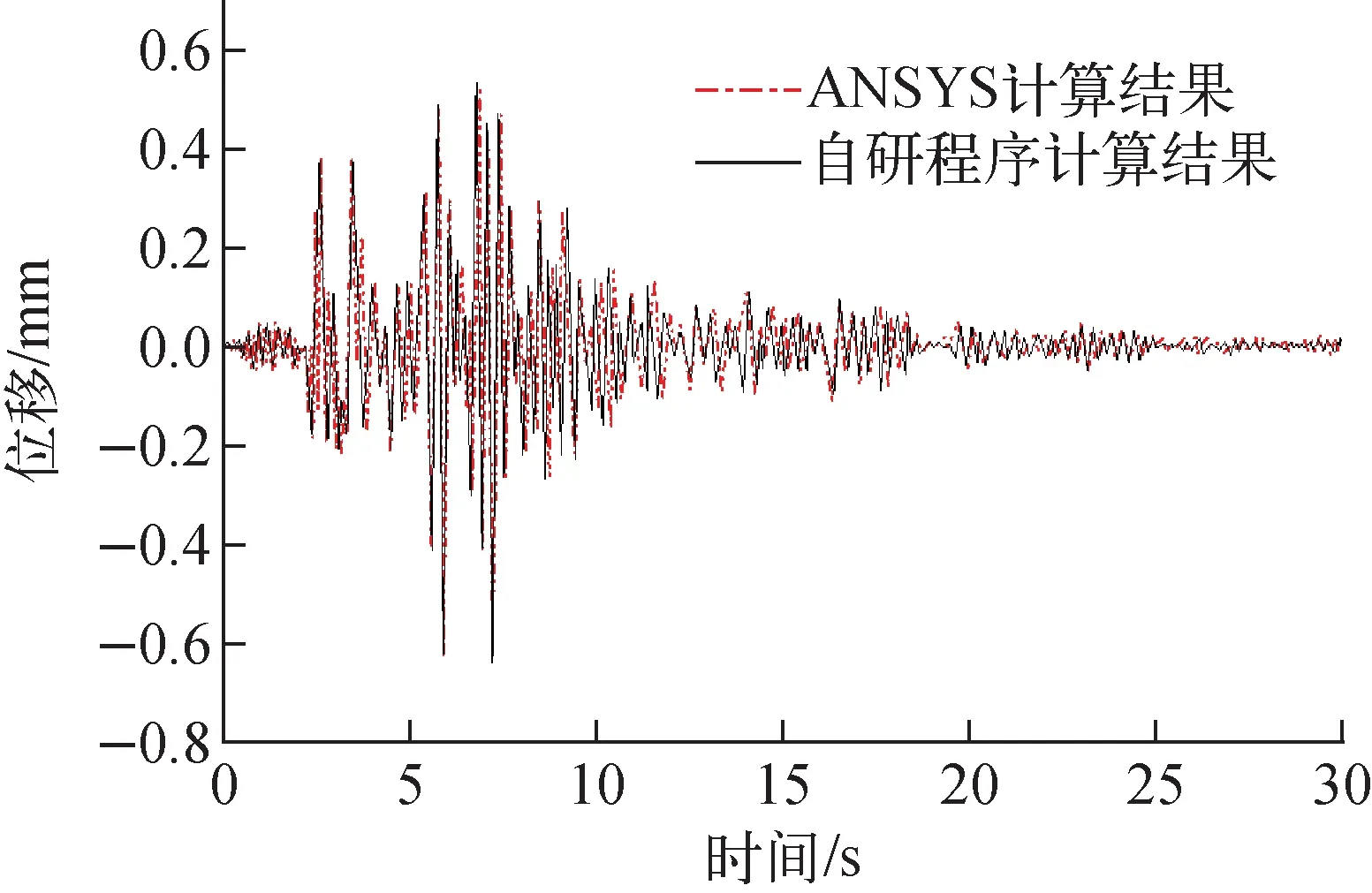
圖4 ANSYS與自研程序對CEFR單組件時程分析結果對比Fig.4 Comparison between time historical calculation results calculated by ANSYS and code

2.4 RAPSODIE堆單排19組件空氣中時程分析驗證

IAEA于1987年到1995年以法國、日本和意大利快堆堆芯抗震試驗為基準組織并開展了各成員國快堆堆芯抗震程序對比驗證的大型會議活動,試驗的組織情況列于表4。

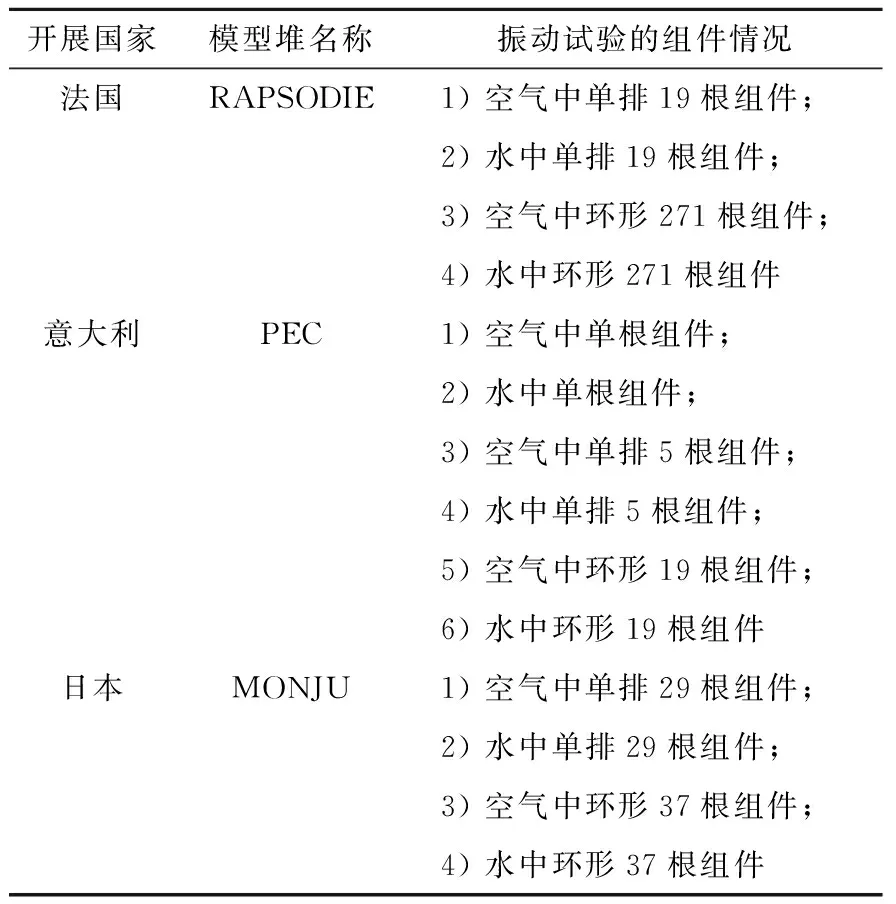
表4 IAEA試驗組織情況Table 4 Model reactor and seismic testconducted by IAEA

為驗證相鄰組件碰撞時碰撞剛度和阻尼設置的正確性,采用表4中法國RAPSODIE堆空氣中單排19根組件碰撞試驗數據對自研程序進行驗證。該試驗包含燃料組件(F/A)和屏蔽組件(N/S),排列方式如圖5所示。組件上下兩個碰撞墊塊分別位于1.28 m和0.71 m處,燃料組件的1階、2階阻尼比為3%,屏蔽組件的1階、2階阻尼比為1%,梁截面參數與試驗測得的碰撞剛度和碰撞阻尼參考日本FINDS程序的設置[2]。

在自研程序中,燃料組件與屏蔽組件底端均設置為固定約束,而燃料組件在管腳球形密封處設置一個剛度為6×106N/m的彈簧以等效間隙帶來的影響,計算固有頻率并與試驗結果對比,如表5所列。可發現,第1階固有頻率程序計算結果和試驗結果符合良好。試驗未給出第2階和第3階固有頻率。

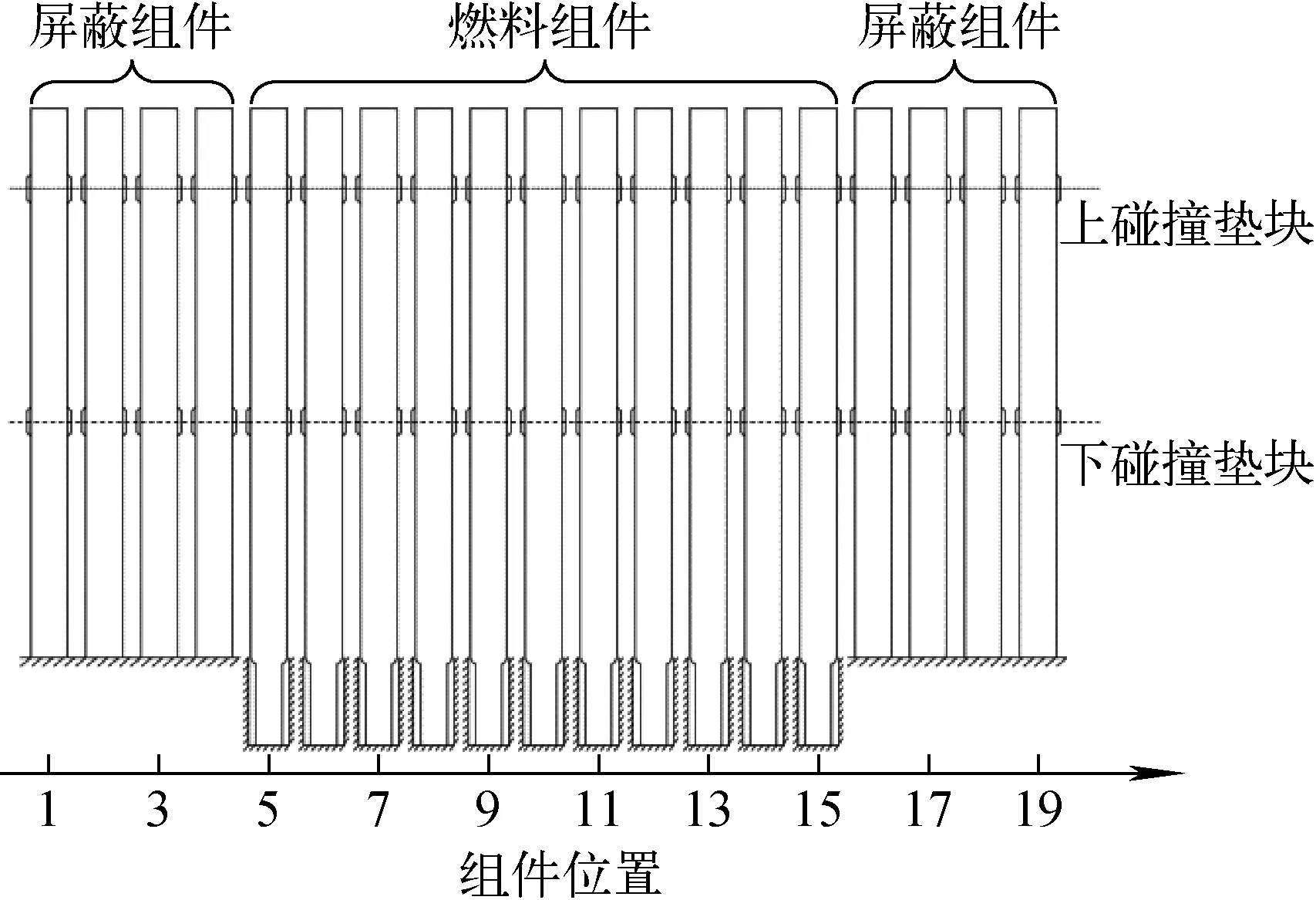
圖5 RAPSODIE單排試驗排列簡圖Fig.5 Layout of RAPSODIE reactor in single row assemblies test

表5 程序計算和試驗所測固有頻率對比Table 5 Comparison between natural frequency results calculated by code and measured from test

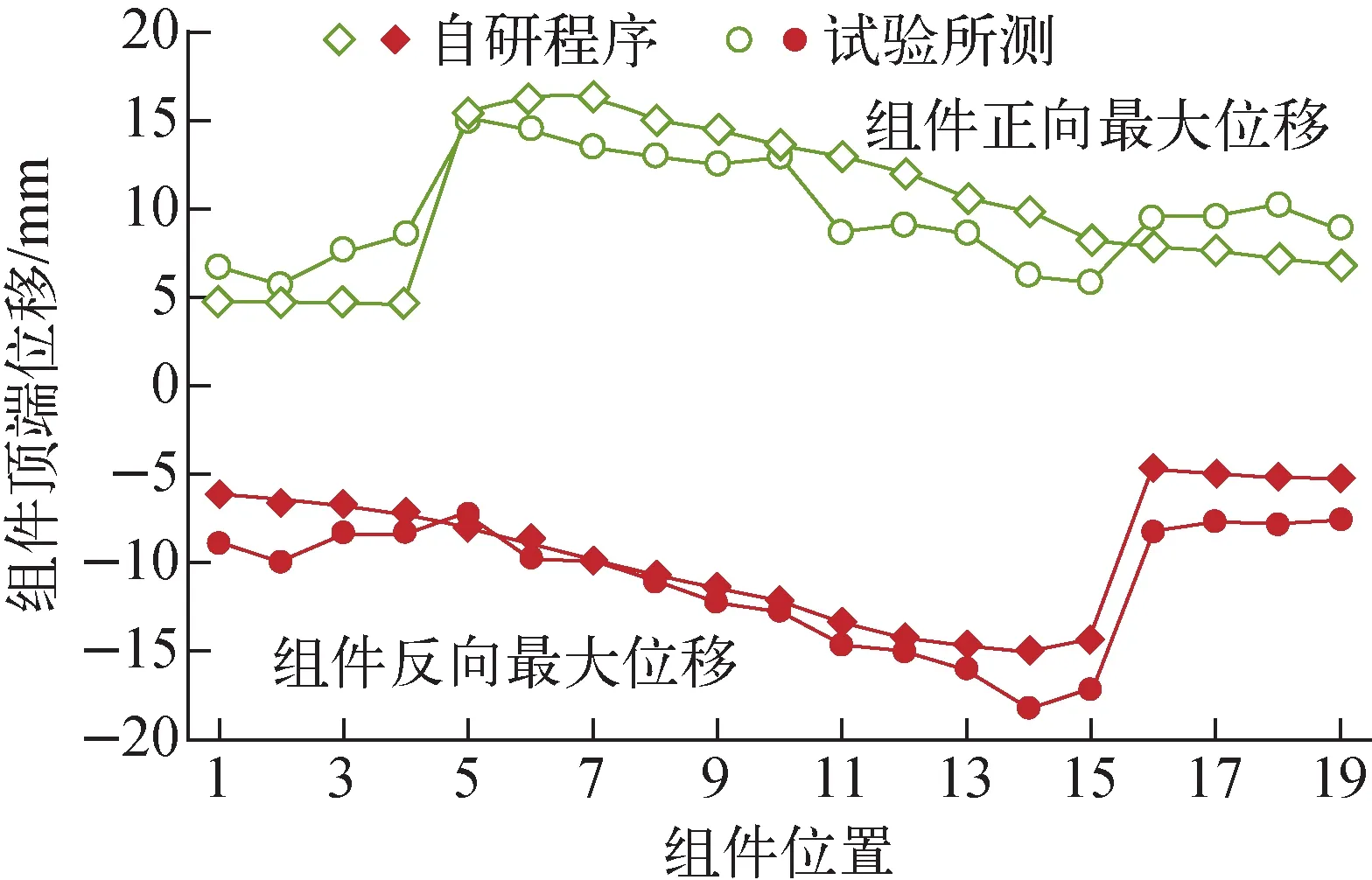
圖6 程序計算和試驗所測組件最大位移對比Fig.6 Comparison between max assembly displacement calculated by code and measured from test

將水平地震波RAP087[2]輸入自研程序,在考慮組件間碰撞的情況下進行時程計算,提取每根組件頂部的最大位移并和試驗所測結果作對比,如圖6所示。可看出二者計算結果接近,其中燃料組件的最大位移基本吻合,誤差主要出現在屏蔽組件上,但堆芯抗震更加關注燃料組件的沖擊與變形,因此證明程序時程分析法的計算結果是可靠的。

3 結論

本文在國內外快堆抗震程序開發和試驗驗證調研的基礎上,建立了快堆堆芯抗震理論模型,闡述了堆芯組件等效簡化以及碰撞剛度和阻尼處理方法,解決了堆芯組件多點復雜非線性碰撞的關鍵性問題,選擇適用于快堆堆芯組件在地震載荷作用下的隱式Newmark法進行了時程分析計算,提出了快堆單排組件抗震分析理論算法,并將該理論算法進行代碼開發。通過從簡單懸臂梁到復雜變截面簡支梁的固有頻率計算,以及單組件和單排多組件的時程分析計算,從下而上逐步驗證了本文所建立的抗震模型和算法的正確性。后續將進一步考慮液體對組件運動的流固耦合影響并將二維算法擴展到三維,拓展程序適用范圍的同時提高計算精度。