具有非單調(diào)發(fā)生率的隨機(jī)離散SIR傳染病模型的穩(wěn)定性

譚偉,劉茂省

(中北大學(xué) 理學(xué)院,太原 030051)

自古以來,人類就飽受各種傳染病的困擾.通常,傳染病可以通過空氣、水、食物、接觸、垂直傳播(母嬰傳播)、體液傳播等方式在人與人之間或人與動(dòng)物之間廣泛傳播.傳染病不但會(huì)影響人們的正常生活,人們的生命安全還會(huì)遭受嚴(yán)重威脅.因此,傳染病的預(yù)防和控制已成為研究的熱點(diǎn).

傳染病研究的開始,人們普遍認(rèn)為是Daniel Bernoulli在1760年對天花疫苗接種的研究,對確定性傳染病數(shù)學(xué)模型的研究早在20世紀(jì)初就開始了.直到1927年,文獻(xiàn)[1-2]在研究倫敦流行的黑死病時(shí)提出了SI艙室模型,然后在1932年建立了SIS模型,對傳染病動(dòng)力學(xué)的研究做出了重要的貢獻(xiàn).之后許多學(xué)者對一些傳染病模型進(jìn)行了廣泛的研究,例如SIS模型和SIR模型[3-6].且SIR傳染病模型是傳染病動(dòng)力學(xué)中重要的數(shù)學(xué)模型之一[4-6].近幾十年來,許多學(xué)者建立了基于具有隨機(jī)擾動(dòng)的確定性模型的隨機(jī)流行病模型[6-8],并在近年來,越來越多的學(xué)者關(guān)注到差分方程模型[9-11].然而,大多數(shù)的學(xué)者都是將隨機(jī)模型和離散模型分別建模來研究的,如文獻(xiàn)[6,11],在流行病學(xué)中對差分方程所描述的隨機(jī)離散模型的穩(wěn)定性的研究很少.所以在本文中,主要是對隨機(jī)離散的傳染病模型進(jìn)行研究.

1 準(zhǔn)備知識(shí)

一般的確定性SIR傳染病模型可以用以下常微分方程來表示[12]:

(1)

其中,S(t),I(t)和R(t)分別代表t時(shí)刻易感者、染病者和恢復(fù)者的數(shù)量.α為種群的招募率,β為疾病的傳播率,μ為人群的自然死亡率,γ為感染個(gè)體的恢復(fù)率,α,β,μ,γ均為正參數(shù).

傳染率在流行病學(xué)中對研究起著至關(guān)重要的作用,改進(jìn)流行病中的傳染率更利于刻畫傳染病的傳播機(jī)制.現(xiàn)實(shí)中的情況是,隨著時(shí)間的推移,當(dāng)傳染病開始暴發(fā)時(shí),政府實(shí)施的各種防治策略和個(gè)人預(yù)防和控制疫情的意識(shí)逐漸增強(qiáng),從而對疫情的發(fā)病率有更強(qiáng)的抑制作用.為了使系統(tǒng)(1)具有更好的現(xiàn)實(shí)意義,在系統(tǒng)(1)的基礎(chǔ)上,文獻(xiàn)[12]進(jìn)一步研究了具有非單調(diào)發(fā)生率的SIR傳染病模型.模型能被表示為:

(2)

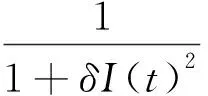
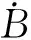
假設(shè)隨機(jī)擾動(dòng)強(qiáng)度與狀態(tài)S(t)和狀態(tài)I(t)在平衡點(diǎn)處的偏差成正比,也就是說當(dāng)系統(tǒng)狀態(tài)偏離平衡點(diǎn)的偏差增加時(shí),隨機(jī)擾動(dòng)強(qiáng)度也會(huì)增加[18].并且這種隨機(jī)噪聲已經(jīng)被許多學(xué)者應(yīng)用于不同的數(shù)學(xué)模型[19-20].在上述假設(shè)下,將系統(tǒng)(2)加上隨機(jī)白噪聲后的表達(dá)式為:

(3)

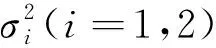
通常用Euler-Marryama方法[21]對連續(xù)模型進(jìn)行離散化,這種方法在之前就已經(jīng)被許多學(xué)者所應(yīng)用[22-23].現(xiàn)在對系統(tǒng)(3)用Euler-Marryama方法進(jìn)行離散化,得到:

(4)

其中h>0是時(shí)間步長,且初始條件為S(0)=φ1(0),I(0)=φ2(0).并且在完備的概率空間(Ω,F,P)中,Fn∈F,n∈Z=(0,1,2,…)是一個(gè)σ代數(shù)簇.通常由E來表示數(shù)學(xué)期望,ωi(n+1)(i=1,2)(n∈Z)是一個(gè)在F中相互獨(dú)立的隨機(jī)序列且服從標(biāo)準(zhǔn)正態(tài)分布,并且對于ωi(n+1)(i=1,2,n∈Z),滿足

(5)

因?yàn)橄到y(tǒng)(4)中有關(guān)R的第3個(gè)式子并不影響對其動(dòng)力學(xué)行為的研究,所以將其忽略,只對以下系統(tǒng)進(jìn)行研究:

(6)

對系統(tǒng)(6)的正平衡點(diǎn)Ee進(jìn)行平移變換,u(n)=S(n)-S*,v(n)=I(n)-I*.然后可以得到以下系統(tǒng):

(7)

系統(tǒng)(7)的零解與系統(tǒng)(6)的正解Ee=(S*,I*)是等價(jià)的.

將正平衡點(diǎn)進(jìn)行平移變換到原點(diǎn)后,然后在點(diǎn)u(n)=0,v(n)=0處對系統(tǒng)(7)進(jìn)行線性化.就可以用以下形式來表示系統(tǒng)(6)在平衡點(diǎn)Ee=(S*,I*)下的線性近似系統(tǒng):

(8)

(9)

(10)

令φ(n)=(u(n),v(n))T,z(n)=(x(n),y(n))T,φ(n)=(φ1(n),φ2(n))T,T代表轉(zhuǎn)置.

為了更好地研究系統(tǒng)的動(dòng)力學(xué)行為,將引入文獻(xiàn)[24] 中的一些重要的定義和定理.

定義1(文獻(xiàn)[24]定義7.1) 系統(tǒng)(7)或(9)是依概率穩(wěn)定的,如果對任意的ε1>0和ε2>0存在一個(gè)δ>0使得系統(tǒng)(7)或(9)的解φ(n)=φ(n,φ)滿足不等式P{supn∈Z|φ(n)|>ε1}<ε2對任意初始函數(shù)S(0)=φ1(0),I(0)=φ2(0)使得P{|φ|<δ}=1.

對一個(gè)任意的非負(fù)函數(shù)Vi=V(i,z(0),z(1),…,z(i)),i∈Z,定義ΔVi為

ΔVi=V(i+1,z(0),z(1),…,z(i+1))-V(i,z(0),z(1),…,z(i)).

定理1(文獻(xiàn)[24]定理1.1) 對于線性系統(tǒng)(8)或(10),若存在一個(gè)非負(fù)函數(shù)Vi=V(i,z(0),z(1),…,z(i))滿足條件EV(0,φ)≤c1‖φ‖2和EΔVi≤-c2E|z(i)|2(i∈Z),其中c1和c2是正常數(shù).那么系統(tǒng)(8)或(10)的零解是漸近均方穩(wěn)定的.

現(xiàn)在考慮以下的隨機(jī)差分系統(tǒng):

(11)

其中σ1,σ2是常數(shù),ωi(n+1)(i=1,2)是Fn自適應(yīng)隨機(jī)變量的相互獨(dú)立的序列且滿足條件(5).可以看出系統(tǒng)(8)和(10)的一般形式就是系統(tǒng)(11),因此,為了更加簡便地研究系統(tǒng)(11)解的穩(wěn)定性,令

(12)

矩陣P和D是對稱矩陣.對于實(shí)對稱矩陣P和Q來說,若P-Q是一個(gè)正定矩陣,那么P>Q.

定理2(文獻(xiàn)[24]中定理5.1) 假設(shè)存在一個(gè)正定矩陣P,使得一個(gè)形式為(12)的半正定矩陣D滿足矩陣方程ATDA-D=-P的解,且矩陣P滿足

(13)

那么系統(tǒng)(11)的零解是漸近均方穩(wěn)定的.

證明借助式(12),可以將系統(tǒng)(11)表示為:

z(n+1)=(A+θ(ω(n+1)))z(n),

其中

考慮Lyapunov函數(shù)V(n)=zT(n)Dz(n),所以有

ΔV(n)=V(n+1)-V(n)=zT(n+1)Dz(n+1)-zT(n)Dz(n).

然后計(jì)算ΔV的期望,得到:

EΔV(n)=E(zT(n+1)Dz(n+1)-zT(n)Dz(n))=EzT(n)[(A+θ(ω(n+1)))TD(A+

θ(ω(n+1)))-D]z(n)=EzT(n)[ATDA-D+θT(ω(n+1))Dθ(ω(n+1))]z(n)=

EzT(n)[-P+θT(ω(n+1))Dθ(ω(n+1))]z(n).

根據(jù)式(5),可以求得:

然后根據(jù)式(13),可以得到:

其中c是正數(shù),所以憑借定理1,可以得出系統(tǒng)(11)的零解是漸近均方穩(wěn)定的.證明完成.

接下來,將應(yīng)用定理2來研究系統(tǒng)(6)的正平衡點(diǎn)和邊界平衡點(diǎn)的穩(wěn)定性.

2 正平衡點(diǎn)的穩(wěn)定性

現(xiàn)在應(yīng)用定理2來分析系統(tǒng)(8),它是式(11)的一種特殊形式,在這種情況下,系統(tǒng)(8)的系數(shù)矩陣是

(14)

因?yàn)锳TDA-D=-P,所以可以得到:

(15)

將矩陣A的元素帶入式(15)中有

(16)

根據(jù)式(13),可以得到:

(17)

然后有以下推論.

推論1若存在一個(gè)正定矩陣P,使得條件(17)對于矩陣方程(16)的解(d11,d12,d22)被滿足,并且矩陣D是半正定的,那么系統(tǒng)(8)的零解是漸近均方穩(wěn)定的.因此,對系統(tǒng)(7)的零解來說其就是依概率穩(wěn)定的,這等同于系統(tǒng)(6)的正平衡點(diǎn)Ee是依概率穩(wěn)定的.

α=4,μ=0.06,γ=0.01,β=0.2,δ=0.2,h=0.1.

(18)

并將易感個(gè)體和染病個(gè)體的初始值設(shè)為

S(0)=80,I(0)=20.

(19)

正平衡點(diǎn)Ee可以通過以上參數(shù)值算得Ee=(S*,I*)=(39.18,23.56).通過求解(14)得到:

對于正定矩陣P,取p11=p22=1,p12=0,所以有

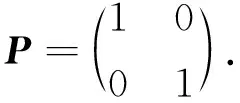
且半正定矩陣D通過求解(16)式得到:

借助推論1,可以了解到如果σ1,σ2滿足以下條件:

(20)

那么,系統(tǒng)(8)的零解是漸近均方穩(wěn)定的.因此,是依概率穩(wěn)定的對于系統(tǒng)(7)的零解,這等同于是依概率穩(wěn)定的對于系統(tǒng)(6)的正平衡點(diǎn)Ee.

接下來,將驗(yàn)證之前的闡述借助數(shù)值仿真.在圖1中展示了噪聲擾動(dòng)強(qiáng)度σ1=σ2=0的情況,圖1(a)和圖1(b)分別表示系統(tǒng)(6)和線性系統(tǒng)(8)的解曲線.

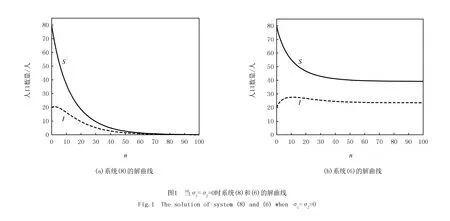
如圖1所示,圖1(a)中線性系統(tǒng)(8)的解曲線最終收斂到0.圖1(b)中系統(tǒng)(6)的解曲線最終收斂于正平衡點(diǎn)Ee=(S*,I*)=(39.18,23.56).因此,通過觀察圖像也可以得出系統(tǒng)(8)的零解是漸近均方穩(wěn)定的,系統(tǒng)(6)的正平衡點(diǎn)Ee是依概率穩(wěn)定的.

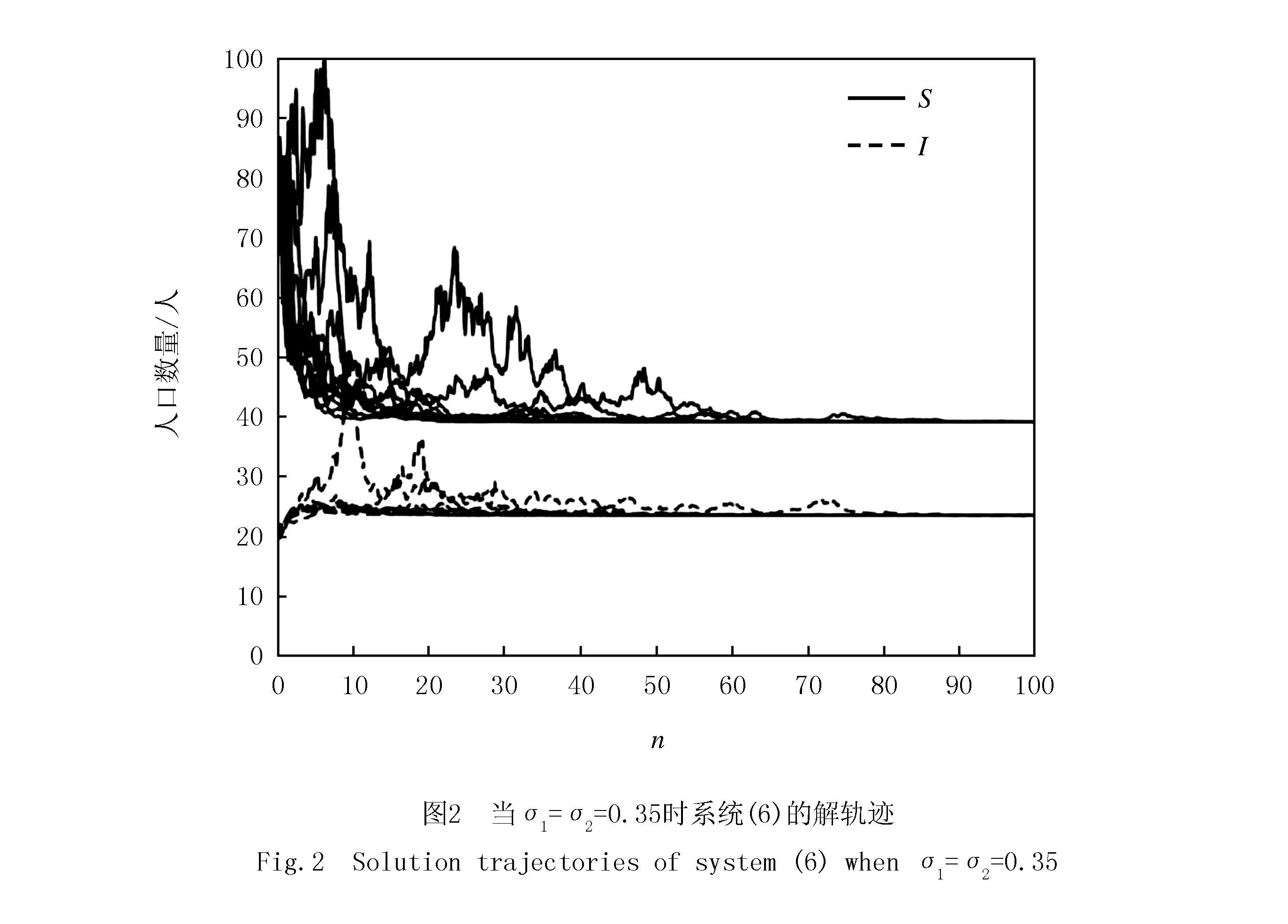
然后將對加入噪聲擾動(dòng)的系統(tǒng)(6)的解進(jìn)行模擬.借助式(18)和(19)中已給出的參數(shù)值和初始值,并且假設(shè)σ1,σ2的值滿足條件式(20),取σ1=σ2=0.35,具有噪聲擾動(dòng)的系統(tǒng)(6)的解軌跡就可以被得到.

從圖2中可以看出,隨機(jī)噪聲并不影響曲線的最終走向,系統(tǒng)(6)的解軌跡最終還是收斂到正平衡點(diǎn)Ee,這就表明系統(tǒng)(6)在正平衡點(diǎn)處是依概率穩(wěn)定的.

3 邊界平衡點(diǎn)的穩(wěn)定性

研究邊界平衡點(diǎn)E0=(S0,I0)的穩(wěn)定性將要借助線性系統(tǒng)(10).類似地,將定理2應(yīng)用于系統(tǒng)(10),在這種情況下,系統(tǒng)(10)的系數(shù)矩陣為

(21)

將矩陣A的元素帶入式(15)中,然后得到

(22)

與推論1類似,根據(jù)式(17),以下推論可以被得到.

推論2對于線性系統(tǒng)(10)的系數(shù)矩陣(21),如果存在一個(gè)正定矩陣P,使方程(22)的解(d11,d12,d22)滿足條件(17),且矩陣D為半正定的,則系統(tǒng)(10)的零解是漸近均方穩(wěn)定的.因此,系統(tǒng)(9)的零解是依概率穩(wěn)定的,這也就是說系統(tǒng)(6)的邊界平衡點(diǎn)E0是依概率穩(wěn)定的.

當(dāng)所選擇的參數(shù)不滿足正平衡點(diǎn)存在的條件時(shí),系統(tǒng)(6)中只有一個(gè)邊界平衡點(diǎn).在這里,取以下參數(shù)值:

α=4,μ=0.1,γ=0.9,β=0.01,δ=0.2,h=0.1.

(23)

并且初始值仍為式(19)中所給出.

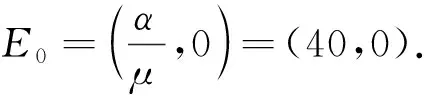
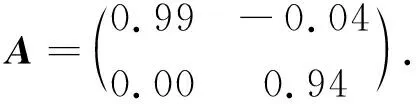
同樣,對于正定矩陣P,仍取p11=p22=1,p12=0,得到

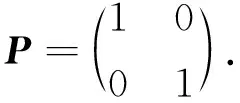
半正定矩陣D的具體形式通過求解方程(22)求得:

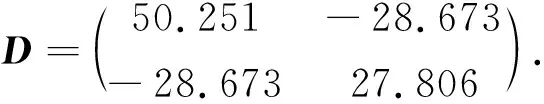
并且如果σ1,σ2滿足以下條件:

(24)

那么,根據(jù)推論2,可以得出系統(tǒng)(10)的零解是漸近均方穩(wěn)定的.因此,是依概率穩(wěn)定的對于系統(tǒng)(9)的零解,這等同于是依概率穩(wěn)定的對于系統(tǒng)(6)的邊界平衡點(diǎn).

根據(jù)式(23)中的參數(shù)值和式(19)給出的初始值,當(dāng)隨機(jī)擾動(dòng)強(qiáng)度為0時(shí),得到系統(tǒng)(6)和(10)的解曲線.如圖3中的(a)和(b)所示.

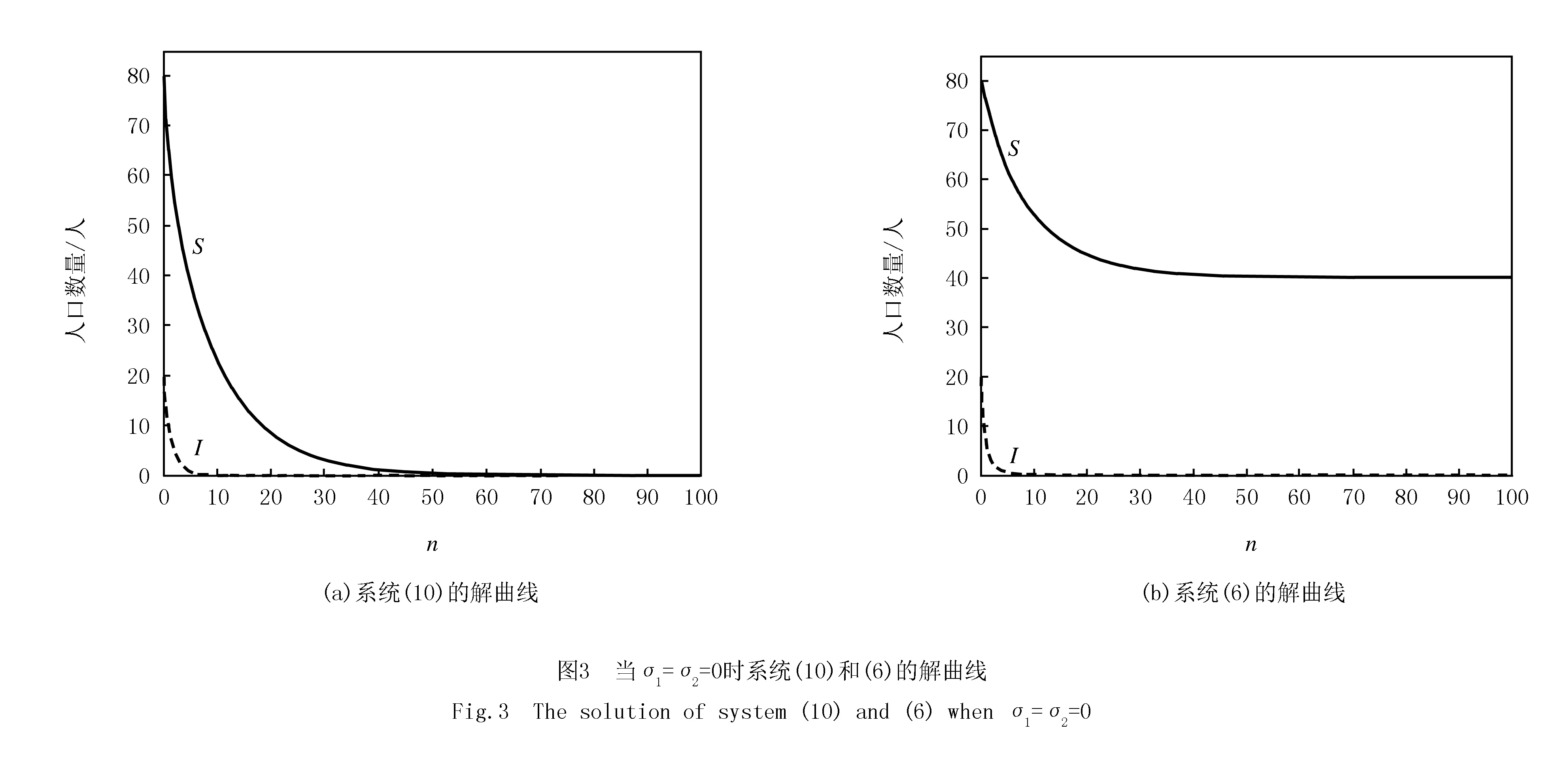
如圖3所示,圖3(a)中線性系統(tǒng)(10)和圖3(b)中系統(tǒng)(6)的解曲線最終都分別收斂到它們的平衡點(diǎn).因此,通過圖像,也可以得到系統(tǒng)(10)的零解是漸近均方穩(wěn)定的,而系統(tǒng)(6)的邊界平衡點(diǎn)E0是依概率穩(wěn)定的.

當(dāng)隨機(jī)噪聲強(qiáng)度不為0,且σ1和σ2的值滿足條件(24)時(shí),取σ1=σ2=0.4,參數(shù)值和初始值仍為式(23)和(19)中給出,然后可以得到具有隨機(jī)噪聲擾動(dòng)的系統(tǒng)(6)的解軌跡.

如圖4所示,可以看到,具有噪聲擾動(dòng)的系統(tǒng)(6)的解軌跡最終收斂于邊界平衡點(diǎn)E0=(40,0),這也表明系統(tǒng)(6)的邊界平衡點(diǎn)是依概率穩(wěn)定的.

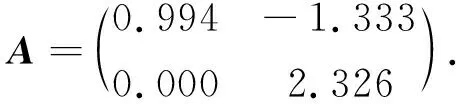
并且P仍為單位矩陣,此時(shí)求得矩陣D為

然而,矩陣D不是一個(gè)半正定矩陣,因此根據(jù)推論2,在這種情況下系統(tǒng)(6)的邊界平衡點(diǎn)是不穩(wěn)定的.

如圖5所示,發(fā)現(xiàn)當(dāng)隨機(jī)噪聲強(qiáng)度為0時(shí),圖5中代表染病者的曲線I是趨向于無窮的,所以此時(shí)系統(tǒng)(10)的零解是不穩(wěn)定的.

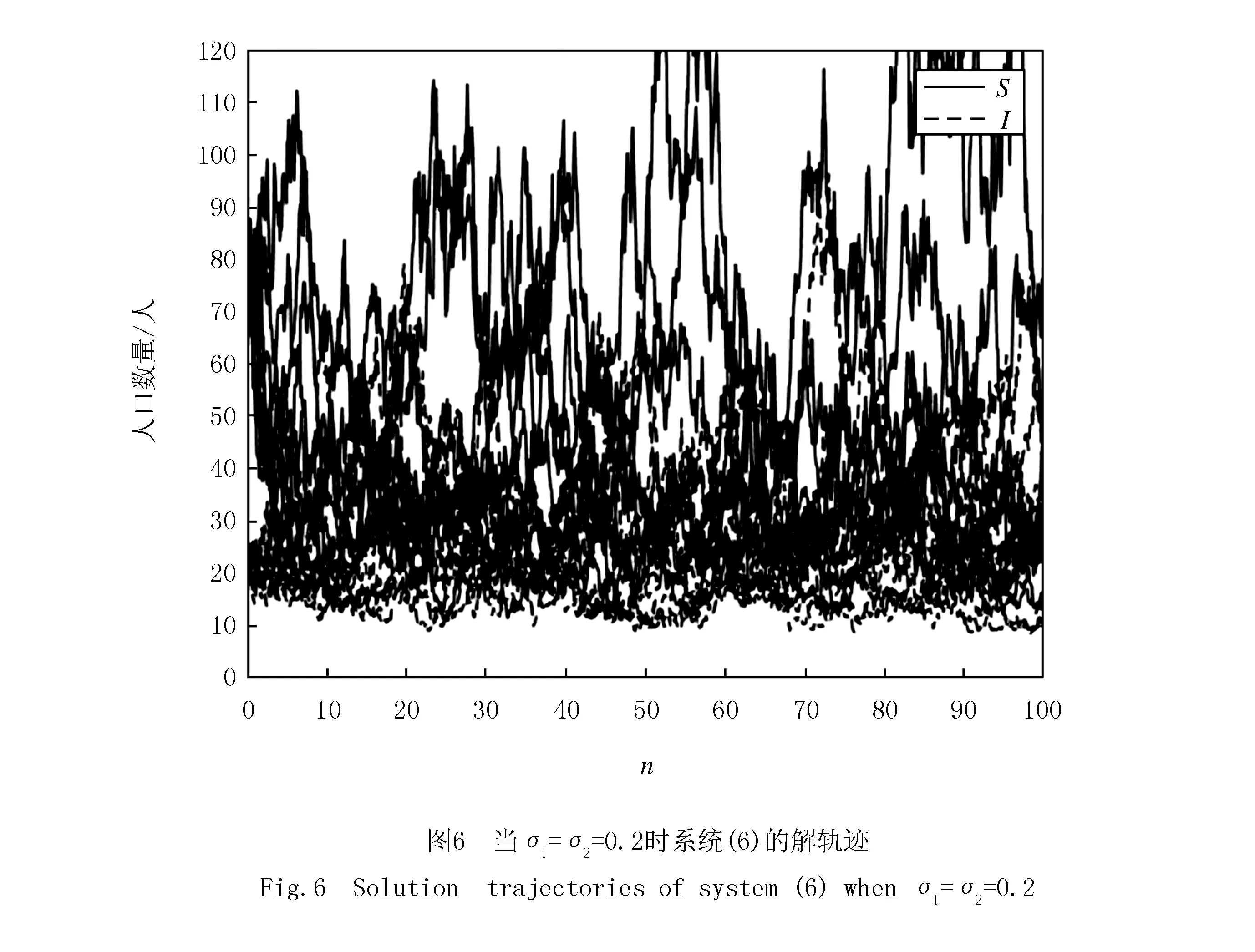
然后在這種情況的基礎(chǔ)上加入隨機(jī)擾動(dòng).如圖6中,當(dāng)加入一個(gè)較小的噪聲強(qiáng)度后,發(fā)現(xiàn)此時(shí)系統(tǒng)的解軌跡在圖中是非常不規(guī)則的.因此,當(dāng)一個(gè)正平衡點(diǎn)存在時(shí),無論隨機(jī)擾動(dòng)是否存在,對于系統(tǒng)(6)來說,它的邊界平衡點(diǎn)都是不穩(wěn)定的.

4 結(jié) 論

本文基于一個(gè)具有非單調(diào)發(fā)生率的SIR傳染病模型,考慮到疾病在傳播過程中不可避免地受到一些隨機(jī)因素的影響,在系統(tǒng)中加入一個(gè)隨機(jī)擾動(dòng)項(xiàng),并假設(shè)隨機(jī)擾動(dòng)強(qiáng)度與狀態(tài)S(t)和I(t)偏離平衡點(diǎn)的偏差成正比.通過應(yīng)用歐拉方法離散化系統(tǒng),得到一個(gè)隨機(jī)離散系統(tǒng).用Lyapunov函數(shù)方法證明了系統(tǒng)在平衡點(diǎn)處穩(wěn)定的充分條件.之后,論證了隨機(jī)離散SIR傳染病模型在正平衡點(diǎn)和邊界平衡點(diǎn)處的穩(wěn)定性.

最后,應(yīng)用數(shù)值仿真對正平衡點(diǎn)和邊界平衡點(diǎn)的穩(wěn)定性進(jìn)行了驗(yàn)證.當(dāng)所選參數(shù)和噪聲強(qiáng)度滿足給定條件時(shí),發(fā)現(xiàn)適當(dāng)?shù)脑肼晱?qiáng)度不會(huì)影響系統(tǒng)在平衡點(diǎn)處的穩(wěn)定性.并且還發(fā)現(xiàn),當(dāng)正平衡點(diǎn)存在時(shí),無論隨機(jī)擾動(dòng)強(qiáng)度是多少,邊界平衡點(diǎn)的穩(wěn)定性都不會(huì)被改變,并且在這種情況下,邊界平衡點(diǎn)是不穩(wěn)定的.