一類非線性中立型廣義彈性桿方程的振動判據
羅李平
(衡陽師范學院 數學與統計學院,湖南 衡陽 421002)
非線性振動問題是近代力學、物理學和工程技術等領域的重要研究課題,如單擺的振動,杠、梁的振動,建筑物和機器的振動,飛行器的結構振動等.在力學上非線性彈性桿(組)結構是工程上最普通的構件之一,廣泛應用于交通工具、傳動軸系、船舶推進、石油鉆探、海底電纜等眾多工程場合,而彈性桿(組)在數學上都是通過偏微分方程(組)來描述的,因此,可以通過對偏微分方程(組)的振動性進行準確分析,從而分析出所對應的機械或部件的振動狀態,這對工程上的機械減振和降噪等實際應用具有重要的理論指導意義.近年來,關于這一方面的研究取得了一些很好的結果,例如文獻[1-2]研究了兩類具泛函變元的二階非線性中立型廣義彈性桿方程的振動性問題;文獻[3-5]研究了幾類具分布時滯的二階中立型廣義彈性桿方程的振動性問題;文獻[6]研究了一類具混合非線性項的二階廣義彈性桿方程的強迫振動性問題;文獻[7-9]研究了幾類具分布時滯的偶數階非線性中立型廣義彈性桿方程(組)的振動性問題.本文擬考慮如下的一類具分布時滯的偶數階非線性中立型廣義彈性桿方程
a1(t)h1(u)Δu+a2(t)h2(u(x,ρ(t)))Δu(x,ρ(t)),(x,t)∈Ω×R+≡G
(1)
解的振動性,其中u=u(x,t),n≥2是偶數,Ω?Rm是有界域,?Ω逐片光滑,R+=[0,∞),且Δ是Rm中的m維Laplacian算子.
同時考慮Dirichlet邊值條件:
u=0,(x,t)∈?Ω×R+.
(2)
本文總假定下列條件成立:
(H1)r(t)∈Cn(R+,R+),0<α<β,0 引理1[10]設y(t)∈Cn([t0,∞),R)為常號,在[t0,∞)上y(n)(t)≠0且滿足y(n)(t)y(t)≤0,則 (i)存在t1≥t0,使得y(i)(t)(i=1,2,…,n-1)在[t1,∞)上常號; (ii)存在l∈{0,1,2,…,n-1},n+l為奇數,使得y(i)(t)>0,t≥t1,i=0,1,2,…,l;(-1)i+ly(i)(t)>0,t≥t1,i=l+1,…,n. 在下文中,總假設邊值問題(1)、(2)的解是整體存在的. 定理1設如下條件成立: (H6)r(t)>1是一個單調遞減函數; 若 (3) 則邊值問題(1)、(2)的所有解在G內振動. 方程(1)兩邊關于x在Ω上積分,有 (4) 由Green公式,邊值條件(2)及(H5)有 (5) (6) 其中N是?Ω的單位外法向量,dS是?Ω上的面積元素. 又由(H2)、(H3)有 (7) (8) (9) 由式(9)有 (10) 從而有 (11) 注意到Z(t)≥r(t)U(t)≥U(t),Z′(t)>0,t≥t2,由式(11)有 (12) 注意到Z′(t)>0,r(t)單調遞減,t≥t2,從t2到t(t>t2)積分(12)可得: 進而有 但這與式(3)矛盾,故定理1得證. 由定理1,有如下推論. 推論1若微分不等式(9)無最終正解,則邊值問題(1)、(2)的所有解在G內振動. 定理3設如下條件成立: 若 (13) 則邊值問題(1)、(2)的所有解在G內振動. 證明如同定理1的證明,可得式(11).注意到r(t)<1,由式(11)有 (14) 注意到Z(t)≥r(t)U(t)≥γU(t),Z′(t)>0,t≥t2,由式(14)有 (15) 注意到Z′(t)>0,t≥t2,從t2到t(t>t2)積分式(15)可得: 進而有 但這與式(13)矛盾,故定理3得證. 類似地,可得如下定理. 定理4設(H8)成立.若 則邊值問題(1)、(2)的所有解在G內振動. 借助如下的特征值引理,可得到許多關于邊值問題(1)、(2)的類似結果.下面,假設h1(u),h2(u)都是常數(不妨假設都是1). 引理2[11]設λ0是如下Dirichlet特征值問題 (16) 的最小特征值,φ(x)是與λ0對應的特征函數,則λ0>0,φ(x)>0,x∈Ω. 定理5設定理1中的條件均滿足,則邊值問題(1)、(2)的所有解在G內振動. 將方程(1)兩邊同乘以Dirichlet問題(16)的最小特征值λ0所對應的特征函數φ(x),并在區域Ω上關于x積分,得 (17) 由Green公式及邊值條件(2),并結合引理2,有 (18) (19) 又由(H2),(H3)有 (20) (21) (22) 由式(22)有 余下證明同定理1的后半部分的證明.故略.定理5證畢. 由微分不等式(22),有 類似于定理5的證明,可得如下定理. 定理6設(H6)、(H7)成立.若 則邊值問題(1)、(2)的所有解在G內振動,其中λ0由問題(16)確定. 由微分不等式(22),有 類似于定理5的證明,可得如下定理. 定理7設(H6)、(H7)成立.若 則邊值問題(1)、(2)的所有解在G內振動,其中λ0由問題(16)確定. 由定理5,有如下推論. 推論2若微分不等式(22)無最終正解,則邊值問題(1)、(2)的所有解在G內振動. 類似地,可得如下定理. 定理8設定理3中的條件均滿足,則邊值問題(1)、(2)的所有解在G內振動. 定理9設(H8)成立.若 則邊值問題(1)、(2)的所有解在G內振動,其中λ0由問題(16)確定. 定理10設(H8)成立.若 則邊值問題(1)、(2)的所有解在G內振動,其中λ0由問題(16)確定. 注1定理6、定理9中的判據僅依賴于擴散系數a2(t). 注2利用本文的思想,還可以考慮其他邊值條件.譬如,考慮如下的Robin邊值條件 (23) 其中μ(x)∈C(?Ω,(0,∞)).只要將文中的假設條件(H5)改為: 不難得到邊值問題(1)、(23)的若干振動判據.限于篇幅,在此省略之. 下面給出一個例子來闡述本文主要結果的有效性. 例1考慮具分布時滯的四階非線性中立型廣義彈性桿方程 (24) 及邊值條件 u(0,t)=u(π,t)=0,t≥0. (25)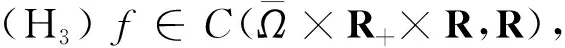

1 主要結果及其證明

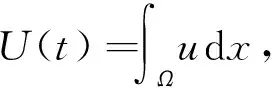







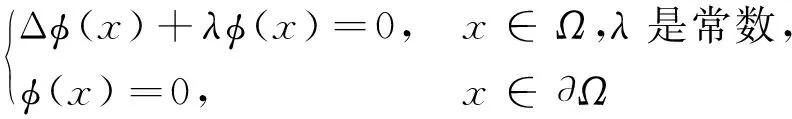
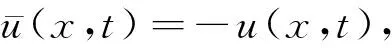
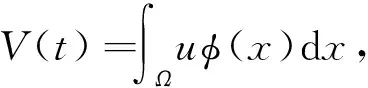






2 應用舉例