在“變”與“不變”中感悟本質

陶芳

摘要：為了讓學生學會從變量的角度認識兩種量之間的關系，初步感受函數的思想方法，《正比例的意義》一課教學，引導學生“變中識不變，變中思不變，變中知不變”。重要的節點包括：比較對照，感悟正比例的意義；多元表征，建構正比例的模型；操作體驗，體會正比例的圖像。

關鍵詞：小學數學；變與不變；《正比例的意義》；函數思想

正比例關系是從對應的角度認識和研究兩種相關聯的量之間“變”與“不變”的規律。“對應”兩個數量之間的“比值不變”是正比例關系的本質屬性。從研究單個量走向多個量，從研究固定（具體）的量走向變化的量，從研究單個數據的靜態情況走向多個數據的動態關系，是學生認識過程中的一次重大飛躍。同時，正比例的知識在日常生活中有著廣泛的應用，學好這部分內容，既可以鍛煉學生用數學的眼光觀察現實生活的意識，提高思考現實問題的能力，又可以為學生初中進一步學習函數知識奠定扎實的基礎。為了讓學生學會從變量的角度認識兩種量之間的關系，初步感受函數的思想方法，《正比例的意義》一課教學，引導學生“變中識不變，變中思不變，變中知不變”。

一、教學過程

（一）理解正比例意義中的“變”

1.通過猜拳游戲，理解“相關聯”

（課始，教師讓學生同桌玩“石頭剪刀布”的游戲，贏一次得5分，共玩9次。游戲結束后，全班匯報得分。）

師 得分的多少和獲勝的次數是有聯系的。獲勝的次數多，得分也多；獲勝的次數少，得分也少。像這樣“一種量變化，另一種量也隨著變化”，我們稱這兩種量為“相關聯的量”。

2.舉例與辨析

師 生活中相關聯的量很多。（出示一輛汽車勻速行駛的時間和路程對照表，見表1）請大家認真研究：表格中有哪兩種量？

生 行駛的時間和路程。

師 它們是相關聯的量嗎？為什么？

生 汽車行駛的時間長，行駛的路程也長，行駛的時間和路程同時增加；時間短，路程也短，時間和路程同時減少。所以，時間和路程是相關聯的量。

師 行駛的時間和路程的變化是——

生 一致的。

師 請帶著這樣的思路繼續研究這幾張表中的數據。

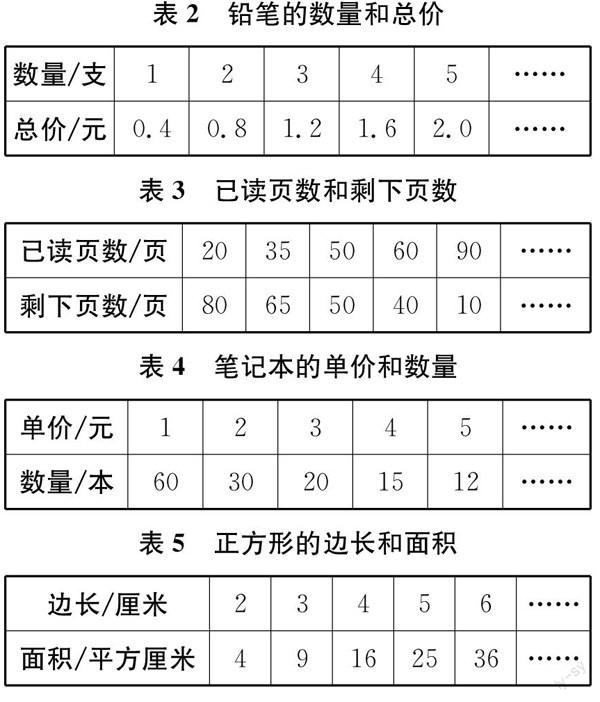
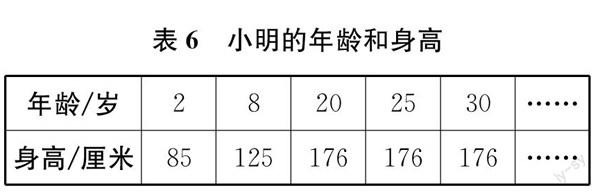
（依次出示購買一種鉛筆的數量和總價、讀一本書時的已讀頁數和剩下頁數、用同樣多的錢購買不同的筆記本的單價和數量、正方形的邊長和面積、小明的年齡和身高等對照表，見表2—表6。）

生 鉛筆的數量和總價變化方向一致，二者是相關聯的量。

生 已讀頁數和剩下頁數變化方向不一致，但二者是相關聯的量。

生 筆記本單價和數量變化方向不一致，但二者是相關聯的量。

生 正方形的邊長和面積變化方向一致，二者是相關聯的量。

生 小明的年齡和身高不是相關聯的量，因為年齡變化，身高不一定發生變化。

（二）理解正比例意義中的“不變”

1.獨立探究，初步感知意義

師 根據剛才的分類，仔細觀察表1、表2和表5這三張表，其中相關聯的兩種量變化方向都一致，那它們有沒有什么變化規律呢？如果有，又是按什么規律變化的呢？（指表1）先來看表1，路程和時間在變化的過程中有什么規律呢？

（學生計算驗證。）

生 路程和所對應的時間的比值都是80。

師 還真是這樣的，那么，這個比值80就是汽車的——

生 速度。

師 所以，我們還可以用怎樣的數量關系式來表示？

生 路程時間=速度（一定）。

師表2和表5中相關聯的兩種量又有怎樣的變化規律呢？和你的同桌一起說一說，算一算，完成研究單。

（學生交流并完成研究單。）

生 （展示自己的研究單，如下頁圖1所示）表2中總價和數量是兩種相關聯的量，總價和數量的比值是不變的，也就是單價是一定的。數量關系為：總價/數量 =單價（一定）。

生 （展示自己的研究單，如圖2所示）正方形的邊長和面積是兩種相關聯的量，面積隨著邊長的變化而變化，但是面積和邊長的比值是變化的，并不一定。

2.歸納總結，揭示正比例意義

師 同學們，剛才的三張表中，兩種量的變化方向都是一致的，但是對應的兩種量的比值有的一定，有的不一定。當比值一定時，我們就說兩種相關聯的量成正比例關系，這兩種相關聯的量是成正比例的量。比如，路程和時間是兩種相關聯的量，當路程和時間的比值一定，也就是速度一定時，我們就說路程和時間成正比例關系，路程和時間是成正比例的量。（板書：路程和時間成正比例關系）總價和數量成正比例關系嗎？為什么？

生 總價和數量是兩種相關聯的量，總價和對應的數量的比值一定，也就是單價一定，所以總價和數量是成正比例的量。

師 這就是我們今天所要研究的正比例的意義。（板書課題：正比例的意義）比較一下，成正比例關系的兩種相關聯的量有什么特點？（板書：變化的量，不變的量）那正方形的邊長和面積成正比例關系嗎？為什么？

生 正方形的邊長和面積的比值不一定，所以不成正比例關系。

師 看來，兩種相關聯的量，只有比值一定，才成正比例關系。那怎樣來判斷兩種量是否成正比例關系呢？同桌互相說一說。

（學生討論。）

師 看一看兩種量是不是相關聯的量，也就是“變”；算一算相關聯的兩種量的比值是不是一定，也就是“不變”。

3.抽象概括，建立模型

師 像這樣比值一定的式子，寫得完嗎？

生 （齊）寫不完。

師 如果用字母x和 y分別表示兩種相關聯的量，用k表示它們的比值，正比例關系可以用怎樣的式子來表示？

［教師根據學生的回答板書：yx=k（一定）。］

（三）從正比例的意義到正比例的圖像

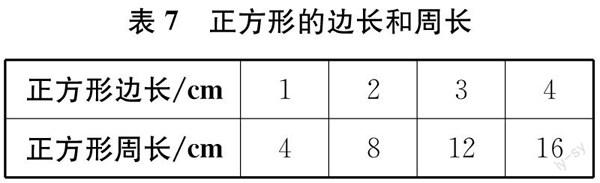
師 判斷正方形邊長和周長是否成正比例。

（學生自主列出表7，并判斷、說理。）

師 （出示下頁圖3）往同一個圓柱形杯子中倒水，水的體積和高度成正比例嗎？為什么？

（學生回答。）

師 （出示下頁圖4）我們發現，當水的體積和高度成正比例關系時，把體積和高度的對應點連起來正好是一條直線。

二、教學思考

（一）“變”中識“不變”：比較對照，感悟正比例的意義

判斷兩個變量是否成正比例，首先要看這兩個量是否相關聯，而判斷的核心是看這兩個變量在變化過程中，比值是否一定。所以，讓學生明確研究的方向是兩個變量的比值，是本節課的關鍵。課始，采用學生喜歡的猜拳游戲引入，為“兩種相關聯的量”進行思維預熱。接著，選擇6個具有較強對比性的學習素材，讓學生判斷每份材料中的兩種量是否相關聯。學生在比較、反思中逐步發現，“相關聯”的概念還是比較寬泛的，無論是變化方向相同還是變化方向相反，只要是一個量變化，另一個量也隨著變化，這樣的兩個量就是相關聯的量。學生在研究變化規律時發現，有的是比值一定，有的是乘積一定，有的是和一定，有的是差一定，從而在對比中主動確定研究的方向，總結出成正比例的兩個量在變化過程中的不變為比值一定。

（二）“變”中思“不變”：多元表征，建構正比例的模型

函數有三種數學表示方法：表格、解析式和圖像。本課的教學從表格和列式切入，對數量關系進行抽象的梳理，從中認識常量和變量的主要特征，并概括出變量關系的共同特征。學生學習兩個現實情境中的正比例關系之后，教師通過富有啟發性的問題，引導學生比較、提取共同的本質：都有兩種相關聯的量，對應數量的比值不變，都成正比例關系。在此基礎上，引導學生學習用解析式符號表征正比例關系，從而在抽象層面認識正比例關系的本質。而練習再次聯系生活，結合相似圖形，孕伏呈現函數圖像。多元表征，讓概念更加飽滿豐盈。

（三）“變”中知“不變”：操作體驗，體會正比例的圖像

“正比例的圖像”主要是下一課時的教學內容，而本節課的練習環節，通過水的體積和高度，引導學生將相對應的點連起來，初步感知正比例的圖像呈一條直線。引入圖像，更能讓學生在數形結合中體驗變與不變的函數思想、一一對應思想、極限思想等，同時也為下一課時的學習做了鋪墊。在學生認識各點含義的基礎上，引導學生連點成線，體驗正比例圖像的形成過程，讓正比例關系的內涵 “看得見”。教學時，可從“往大”和“就小”兩個方面追問：比圖中時間更大的點還有嗎？比圖中路程更小的點呢？引導學生更好地感知符合不變規律的“每組數”的無限性，在圖像的延伸中使正比例的內涵“看得清”。這樣，學生初步認識到兩個數量的正比例關系既可以通過具體的數據體現出來，也可以通過直觀的圖像表現出來。從正比例的圖像再回頭看正比例的意義，無疑更能加深學生對正比例意義的理解，使學生從具體形象的靜態認識，上升到動態建構的過程。