2023年全國高考三角命題預測

梁業興

縱觀近年高考，三角內容的命題往往是“兩小一大”，且“一大”常規會與解三角形、平面向量結合.試題難度中等及以下，對于考生來說是基礎題、是普遍可以得分之題.因此，此類題很重要，它才是真正拉開距離的題，為了確保你不被對手“拉開”，你必須保證這些題“毫無懸念”的產生正確結論.它是你的“助力器”，它從命題的角度，結合試題類型進行全方位的剖析與預測，對你的復習與提升將會有幫助，請仔細往下看：

預測一：從基本技能入手，設計精巧的客觀性試題

三角中的客觀性試題并不一定都是基礎題、簡單題，有時它會與其它章節的知識結合在一起，從某一基本知識點或某一技能處進行設計，往往試題新穎、獨特，求解艱苦有難度也有靈活性.

例1.（1）已知函數f（x）=3sin（2ωx+π3）（ω>0）的

圖像與x軸相鄰兩個交點的距離為π2.若將f（x）的圖像向

左平移m（m>0）個單位長度得到函數g（x）的圖像恰好經過點（－π3，0），則當m取得最小值時，g（x）在［－π6，7π12］上的單調遞增區間為______．

（2）已知α，β，γ是互不相同的銳角，則在sinαcosβ，sinβcosγ，sinγcosα三個值中，大于12的個數的最大值是（）

A. 0

B. 1

C. 2

D. 3

（3）如圖，圓O的半徑為1，A是圓上的定點，P是圓上的動點，角x的始邊為射線OA，終邊為射線OP，過點P作直線OA的垂線，垂足為M，將點M到直線OP的距離表示為x的函數f（x），則y=f（x）=＼[0，π＼]上的圖像大致為（）

解析：（1）由函數f（x）的圖像與x軸相鄰兩個交點的距離為π2，得函數f（x）的最小正周期為T=2π2ω=πω=1，函數f（x）的解析式為f（x）=3sin（2x+π3）.將f（x）的圖像向左平移m（m>0）個單位長度得到函數g（x）=3sin［2（x+m）+π3］的圖像，根據g（x）的圖像恰好經過點（－π3，0），得sin2（－π3+m）+π3=0即m=kπ2+π6（k∈Z）.

因為m>0，所以m的最的小值為π6.此時，g（x）=3sin2x+2π3.

因為x∈－π6，7π12，所以2x+2π3∈π3，11π6.

當2x+2π3∈π3，π2，即x∈－π6，－π12時，g（x）單調遞增.

當2x+2π3∈3π2，11π6，即x∈5π12，7π12時，g（x）單調遞增．

綜上，g（x）在區間－π6，7π12上的單調遞增區間是－π6，－π12和5π12，7π12.

（2）由基本不等式有sinαcosβ≤sin2α+cos2β2，同理sinβcosγ≤sin2β+cos2γ2，sinγcosα≤sin2γ+cos2α2，

故sinαcosβ+sinβcosγ+sinγcosα≤32，故sinαcosβ，sinβcosγ，sinγcosα不可能均大于12.取α=π6，β=π3，γ=π4，則sinαcosβ=14<12，sinβcosγ=64>12，sinγcosα=64>12，

故三式中大于12的個數的最大值為2．故選C.

（3） 如下圖：過M作MD⊥OP于Ｄ，則 PM=｜sin x｜，

OM=cosx，在Rt△OMP中

，MD=OM·PMOP=cosx·sinx1=cosxsinx=12sin2x，

∴f（x）=12sin2x（0≤x≤π），選B.

點評：（1）本題包含了函數圖像的多種基本性質，稍有不慎或有一處不過關，想產生結論都非常困難.（2）本題基本不等式與同角三角函數關系的巧妙結合，再加上一定的分析判斷，恰到好處地產生了結論.（3）本題隱含了函數的解析式，如果你能順利地產生函數解析式，最后產生結論就易如反掌.

預測二：設計多選題，從多角度、多層次考查基礎知識與基本技能

多選題對于數學（Ⅰ）卷來說是后起之秀，雖然才進入試卷兩年，但已引起了全體數學教師及高考命題人員的廣泛關注.它可以橫向考查多個知識點與技能點，有一個未掌握或未理解，本題你可能就只得兩分.也可以縱向考查對某一知識與技能掌握的深度，尚若深度未達標，得分也很少.三角是設計各種類型多選題的“良田”，一定要引起我們重視.

例2.（1）使sinαcosβ=－13，使cosαsinβ成立的一個必要不充分條件是 （）

A.－23，43______

B.－34，34

C.－43，43

D.－23，23

（2）已知定義域為R的函數f（x）滿足f（1+x）+f（1－x）=0，函數g（x）=f（x）sinωx（ω>0），若函數y=g（x+1）為奇函數，則ω的值可以為（）

A.π4

B. π2

C.π

D. 3π2

（3）對于函數f（x）=sinπx，0≤x≤212f（x－2），x>2下列結論中正確的是（）

A.任取x1，x2∈［1，+），都有|f（x1）－f（x2）|≤32

B. f（12）+f（52）+…+f（12+2k）=2－12k+1，其中k∈N

C.f（x）=2kf（x+2k）（k∈N*）對一切x∈［0，+）恒成立

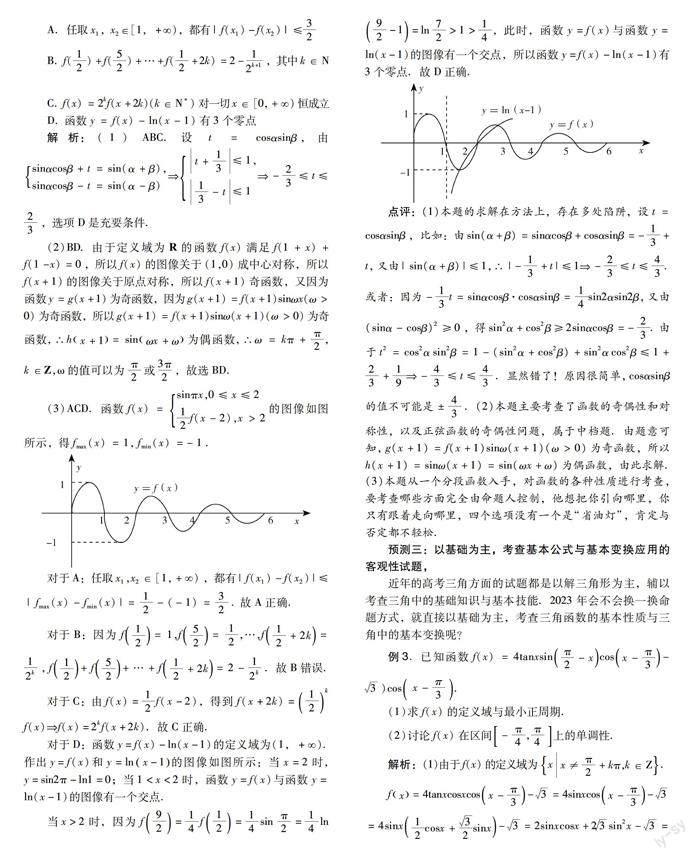
D. 函數y=f（x）－ln（x－1）有3個零點

解析：（1）ABC.設t=cosαsinβ，由sinαcosβ+t=sin（α+β），

sinαcosβ－t=sin（α－β）t+13≤1，

13－t≤1－23≤t≤23，選項D是充要條件.

（2）BD.由于定義域為R的函數f（x）滿足f（1+x）+f（1－x）=0，所以f（x）的圖像關于（1，0）成中心對稱，所以f（x+1）的圖像關于原點對稱，所以f（x+1）奇函數，又因為函數y=g（x+1）為奇函數，因為g（x+1）=f（x+1）sinωx（ω>0）為奇函數，所以g（x+1）=f（x+1）sinω（x+1）（ω>0）為奇函數，∴hx+1=sinωx+ω為偶函數，∴ω=kπ+π2，k∈Z，ω的值可以為π2或3π2，故選BD．

（3）ACD.函數f（x）=sinπx，0≤x≤2

12f（x－2），x>2

的圖像如圖所示，得fmax（x）=1，fmin（x）=－1．

對于A：任取x1，x2∈［1，+），都有|f（x1）－f（x2）|≤|fmax（x）－fmin（x）|=12－（－1）=32.故A正確.

對于B：因為f12=1，f52=12，…，f12+2k=12k，f12+f52+…+f12+2k=2－12k.故B錯誤.

對于C：由f（x）=12f（x－2），得到f（x+2k）=12kf（x）f（x）=2kf（x+2k）.故C正確.

對于D：函數y=f（x）－ln（x－1）的定義域為（1，+）.作出y=f（x）和y=lnx－1的圖像如圖所示：當x=2時，y=sin2π－ln1=0;當1

當x>2時，因為f92=14f12=14sinπ2=14ln92－1=ln72>1>14，此時，函數y=f（x）與函數y=ln（x－1）的圖像有一個交點，所以函數y=f（x）－ln（x－1）有3個零點.故D正確．

點評：（1）本題的求解在方法上，存在多處陷阱，設t=cosαsinβ，比如：由sin（α+β）=sinαcosβ+cosαsinβ=－13+t，又由|sin（α+β）|≤1， ∴|－13+t|≤1 －23≤t≤43.或者：因為－13t=sinαcosβ·cosαsinβ=14sin2αsin2β， 又由（sinα－cosβ）2≥0，得sin2α+cos2β≥2sinαcosβ=－23.由于t2=cos2αsin2β=1－（sin2α+cos2β）+sin2αcos2β≤1+23+19－43≤t≤43 .顯然錯了！原因很簡單，cosαsinβ的值不可能是±43.（2）本題主要考查了函數的奇偶性和對稱性，以及正弦函數的奇偶性問題，屬于中檔題．由題意可知，g（x+1）=f（x+1）sinω（x+1）（ω>0）為奇函數，所以h（x+1）=sinω（x+1）=sin（ωx+ω）為偶函數，由此求解．（3）本題從一個分段函數入手，對函數的各種性質進行考查，要考查哪些方面完全由命題人控制，他想把你引向哪里，你只有跟著走向哪里，四個選項沒有一個是“省油燈”，肯定與否定都不輕松.

預測三：以基礎為主，考查基本公式與基本變換應用的客觀性試題，

近年的高考三角方面的試題都是以解三角形為主，輔以考查三角中的基礎知識與基本技能.2023年會不會換一換命題方式，就直接以基礎為主，考查三角函數的基本性質與三角中的基本變換呢？

例3.已知函數f（x）=4tanxsinπ2－xcosx－π3－3）cosx－π3.

（1）求f（x）的定義域與最小正周期.

（2）討論f（x）在區間－π4，π4上的單調性.

解析：（1）由于f（x）的定義域為xx≠π2+kπ，k∈Z.

fx=4tanxcosxcosx－π3－3=4sinxcosx－π3－3

=4sinx12cosx+32sinx－3=2sinxcosx+23sin2x－3

=sin2x+31-cos2x－3=sin2x－3cos2x=2sin2x－π3.

所以，fx的最小正周期T=2π2=π.

（2）令z=2x－π3，函數y=2sinz的單調遞增區間是－π2+2kπ，π2+2kπ，k∈Z.

由－π2+2kπ≤2x－π3≤π2+2kπ，得－π12+kπ≤x≤5π12+kπ，k∈Z.

設A=－π4，π4，B=x－π12+kπ≤x≤5π12+kπ，k∈Z，易知A∩B=－π12，π4.

所以，當x∈－π4，π4時，f（x） 在區間－π12，π4上單調遞增，在區間－π4，－π12上單調遞減.

點評：此題很基礎、很簡單，把它設計為解答題的第一題，也就是第17題完全可以.三角函數是以角為自變量的函數，因此解三角函數題，首先從角進行分析，善于用已知角表示所求角，即注重角的變換.角的變換涉及基本公式，選用恰當的公式，是解決三角問題的關鍵. 對于三角函數來說，常常是先化為y=Asin（ωx+φ）+h的形式，再利用三角函數的性質求解．三角恒等變換要堅持結構同化原則，即盡可能地化為同角函數、同名函數、同次函數等，其中切化弦也是同化思想的體現.降次是一種三角變換的常用技巧，要靈活運用降次公式．

預測四：以分析探索為主，設計探索性客觀性試題

探索性試題，一直倍受各級各類考試命題人的青睞，以分析探索為主，設計三角函數的探索性試題也可能是命題方向之一.

例4.已知函數f（x）=sinωx（sinωx+cosωx）－12（ω>0）圖像的相鄰兩條對稱軸之間

的距離為2π．

（1）求f（x）的單調遞增區間以及f（x）圖像的對稱中心坐標.

（2）是否存在銳角α，β，使α+2β=2π3，fα+π2·f2β+3π2=38同時成立？若

存在，求出角α，β的值.若不存在，請說明理由．

解析：（1）由f（x）=sinωx（sinωx+cosωx）－12=22sin2ωx－π4.

因為f（x）圖像的相鄰兩條對稱軸之間的距離為2π，得T=4π=2π2ωω=14.

于是f（x）=22sin12x－π4.

由－π2+2kπ≤12x－π4≤π2+2kπ－π2+4kπ≤x≤3π2+4kπ（k∈Z）.

所以f（x）的單調遞增區間為－π2+4kπ，3π2+4kπ（k∈Z）.

由12x－π4=kπx=2kπ+π2（k∈Z）.

所以f（x）圖像的對稱中心坐標為2kπ+π2，0（k∈Z）.

（2）存在，理由如下：

因為fα+π2=22sinα2，f2β+3π2=22sinβ+π2=22cosβ，

那么fα+π2·f2β+3π2=22sinα2·22cosβ=12sinα2cosβ.

由α+2β=2π3α=2π3－2β，

得sinα2cosβ=sin（π3－β）cosβ=

32cosβ－12sinβcosβ

=32·1+cos2β2－14sin2β=34+34cos2β－14sin2β.

即fα+π2·f2β+3π2=38+38cos2β－18sin2β.

若fα+π2·f2β+3π2=38，則38cos2β－18sin2β=0tan2β=3.

又β為銳角，得β=π6，由α+2β=2π3α=2π3－2β=π3.

點評：本題主要考查了三角函數恒等變換的應用，正弦函數的周期公式，正弦函數的圖像和性質的綜合應用，考查了轉化思想和運算求解能力，屬于較難題．（1）由已知利用三角函數恒等變換的應用可得函數解析式f（x）=22sin2ωx－π4，利用正弦函數的周期公式可求ω的值．進一步得到增區間以及對稱中心．（2）由已知利用三角函數恒等變換的應用可求tan2β=3，結合范圍β為銳角產生結論．

預測五：注重選擇性，設計條件或結論不完備的客觀性試題

條件或結論不完備試題是近年才出現的，由于它具有選擇性，而試題的難易與運算的

繁簡又不可能絕對一致，因此，恰當的選擇（或運氣的選擇）也許會使求解簡單一些，因此，它很受考生喜歡，當然，也受到命題專家的關注.

例5.在①f（x）的圖像關于直線x=5π6ω對稱，②f（x）=cosωx－3sinωx，③

f（x）≤f（0）恒成立這三個條件中任選一個，補充在下面問題中．若問題中的ω存在，求出ω的值，若ω不存在，請說明理由．

設函數f（x）=2cos（ωx+φ）（ω>0，0≤φ≤π2），______，是否存在正整數ω，使

得函數f（x）在0，π2上是單調的？（注：選擇多個條件分別解答，按第一個解答計分）

解析：若選①，令ωx+φ=kπ，k∈Z代入x=5π6ωφ=kπ－5π6，因為0≤φ≤π2，

所以φ=π6，f（x）=2cosωx+π6，當x∈0，π2時，ωx+π6∈π6，πω2+π6.

若函數f（x）在0，π2上單調，則有ωx2+π6≤π0<ω≤53，

所以存在正整數ω=1時，使得函數f（x）在0，π2上單調的;

若選②，f（x）=cosωx－3sinωx=2cosωx+π3φ=π3，

當x∈0，π2時，ωx+π3∈π3，πω2+π3，

若函數f（x）在0，π2上單調，則有πω2+π3≤π0<ω≤43，

所以存在正整數ω=1時，使得函數f（x）在0，π2上是單調的.

若選③，因為f（x）≤f（0）恒成立，即f（x）max=f（0）=2cosφ=2cosφ=1.

因為0≤φ≤π2，所以φ=0此時f（x）=2cosωx，當x∈0，π2時，ωx∈0，πω2，

若函數f（x）在0，π2上單調，則有πω2≤π0<ω≤2，

所以存在正整數ω=1或2時，使得函數f（x）在0，π2上是單調的．

點評：本題考查三角函數的圖像與性質，屬于開放性的中檔題．若選①，要注重在對稱軸處取得最大值或最小值.若選②，要注重“化一公式”的應用.若選③，要注重函數最值的特點．無論選哪一個都需要抓住0，π2是函數的一個單調區間的子區間即可.

預測六：從實際應用入手，設計與生活實際聯系密切的客觀性試題

數學建模是數學的六大核心素養之一，是高考重點考查的內容.用所學知識處理實際應用問題的能力又是數學的重要能力，從實際應用入手設計與生活實際聯系密切的客觀性試題完全在情理之中，當然，要注意試題的難度.

例6.如圖，我市某污水處理廠要在一個矩形污水處理池ABCD

的池底水平鋪設污水凈化管道（Rt△FHE三條邊，H是直角頂點）來處理污水，管道越長，污水凈化效果越好.要求管道的接口H是AB的中點，點E，F分別落在線段BC，AD上，已知AB=20m，AD=103m，記∠BHE=θ．

（1）試將污水凈化管道的總長度L（即Rt△FHE的周長）表示為θ的函數，并求出定義域;

（2）問θ取何值時，污水凈化效果最好·并求出此時管道的總長度．

解析：（1）由題意可得EH=10cosθ，FH=10sinθ，EF=10sinθcosθ，

由于BE=10tanθ≤103，AF=10tanθ≤10333≤tanθ≤3π6≤θ≤π3.

所以L=10cosθ+10sinθ+10sinθcosθ，θ∈π6，π3.

即L=10×sinθ+cosθ+1sinθcosθ，θ∈［π6，π3］.

（2）設sinθ+cosθ=t，則sinθcosθ=t2－12，

由于θ∈π6，π3，t=sinθ+cosθ=2sinθ+π4∈3+12，2，

由于L=10（t+1）t2－12=20t－1在3+12，2上是單調減函數，

所以，當t=3+12時，即θ=π6或θ=π3時，L取得最大值為203+1m.

點評：本題考查三角函數在實際問題中的應用、兩角和與差的三角函數，考查轉化思想以及計算能力，是中檔題，也是完全可能作為考題的題，值得我們關注．

預測七：從新定義入手，設計與基本技能相關的客觀性試題

新定義問題一直是高考命題的熱點，在三角函數中設計一道中檔題，用以考查三角函數的基礎知識與基本技能是一個很好的創意，值得我們關注.

例7.設函數f（x）=cos2x+asinx+a．

（1）當a=1時，求函數f（x）在區間0，π3上的值域;

（2）設函數φ（x）的定義域為I，若x0∈I，且φ（x0）=1，則稱x0為函數y=φ（x）的

“壹點”，已知f（x）在區間［0，2π］上有4個不同的“壹點”，求實數a的取值范圍．

解析：由于f（x）=cos2x+asinx+a=－2sin2x+asinx+a+1，

（1）當a=1時，f（x）=－2sin2x+sinx+2，x∈［0，π3］，易得值域為3+12，178．

（2）由題意可知，－2sin2x+asinx+a+1=1在區間［0，2π］上有4個不同的零點，

令g（x）=－2sin2x+asinx+a，則g（x）在區間［0，2π］上有4個零點，令t=sinx∈［－1，1］，則h（t）=－2t2+at+a，

①若h（t）在（－1，1）上有2個非零零點，則

h（－1）<0，

ha4>0，

h（1）<0，

－1

h（0）≠00

②若h（t）的2個零點為0和1，則

a=0，

a2=1，無解，舍去.

③若h（t）的2個零點為0和－1，則

a=0，

a2=－1，無解，舍去．

綜上所述，0

點評：本題考查了二倍角公式的應用，換元法求三角函數值域，二次函數根的分布，屬于難題．（1）先利用余弦的二倍角公式，將原函數變形，然后換元法，變成關于t的二次函數，再求函數的值域，需要注意新元的取值范圍.（2）將題干描述的“壹點”可以轉化為函數的零點問題來處理，再結合二次函數根的分布，分類討論每種情況．

預測八：從與其他知識點交匯點入手，設計新穎的客觀性試題

試題的交匯性也是高考試題的一大亮點，曾經的概率統計與數列交匯、立幾與導數交匯等都讓人們記憶猶新，其實數學中的所有內容幾乎都是可可交匯的，只是看命題人如何進行設計.

例8.設函數f（x）=2acos2x+（a－1）cosx－1，其中a>0，記|f（x）|的最大值為A．

（1）若a≥1，求A.

（2）證明：|f′（x）|≤2A

解析：（1）當a≥1時，|f（x）|=|2acos2x+（a－1）cosx－1|=|acos2x

+（a－1）（cosx+1）|≤|acos2x|+（a－1）（|cosx|+1）≤a+2（a－1）=3a－2=f（0），

因此，A=3a－2.

（2）當0

則A是|g（t）|在［-1，1］上的最大值.g（-1）=a，g（1）=3a-2，

且當t=1-a4a時，g（t）取得極小值，極小值為g1-a4a=-a2+6a+18a．

令-1<1-a4a<1，得a<-13（舍去），或a>15．

（i）當0

∵|g（-1）|<|g（1）|，∴A=2-3a．

（ii）當150，∴g（-1）>g（1）>g1-a4a．

又∴g1-a4a-|g（-1）|=（1-a）（7a+1）8a>0，∴g1-a4a>|g（-1）|．

∴A=g1-a4a=a2+6a+18a，∴A=2-3a，0

a2+6a+18a，15

3a-2，a≥1

由于f′（x）=－4acosxsinx－（a－1）sinx=－2asin2x－（a－1）sinx，

那么|f′（x）|=|－2asin2x－（a－1）sinx|≤2a+|a－1|.

當0

當151|f′（x）|≤1+a<2A.

當a≥1時，|f′（x）|≤3a－1≤6a－4=2A.

綜上，得|f′（x）|≤2A.

點評：本題將三角函數與導數、不等式交匯在一起，求解過程用到三角基本公式、不等式放縮及復合函數求導等，難度不大，但考點的覆蓋、基本技能的考查都十分到位，可以說是一道比較好的試題.

責任編輯徐國堅