基于hash表的華容道算法研究

周揚 陳伊琳 韋妮君 周一諾

關鍵詞：華容道；時間復雜度；hash表

1引言

目前對華容道算法的優化主要集中在改進搜索策略和減少搜索狀態[1-2]，即基于深度優先或廣度優先的改進。這兩種算法的時間復雜度都為O（V+E）[3]，其中V為頂點數，E為邊數。對于華容道游戲，可以將棋盤上的每個狀態看作一個頂點，最小正方形棋子的大小視為1*1，則棋盤的大小為4*5，共20個位置。為了估算不考慮棋子重合情況，所有狀態數就是在20個位置上放10個棋子的排列，共A=670442572800種狀態，即便除去棋子重合的非法情況，也有65 880種狀態。保守估算1個狀態對應2條邊，則對于華容道游戲頂點和邊總數約為65880*3=197640。深度優先和廣度優先算法本質是在以萬為數量級的狀態中找到最優解。實際情況是，幾個經典開局都要搜索約2萬個狀態，效率較低。

鑒于此，可以考慮：（1）能否求出華容道一共幾種狀態？（2）是否能將所有狀態枚舉出來？（3）存儲所有狀態和對應最優解所需的內存空間能否接受？如果這3個問題都是肯定回答，那么就可以提前將狀態和對應的最優解存人hash表。下文將分析這3個問題。

2基本定義

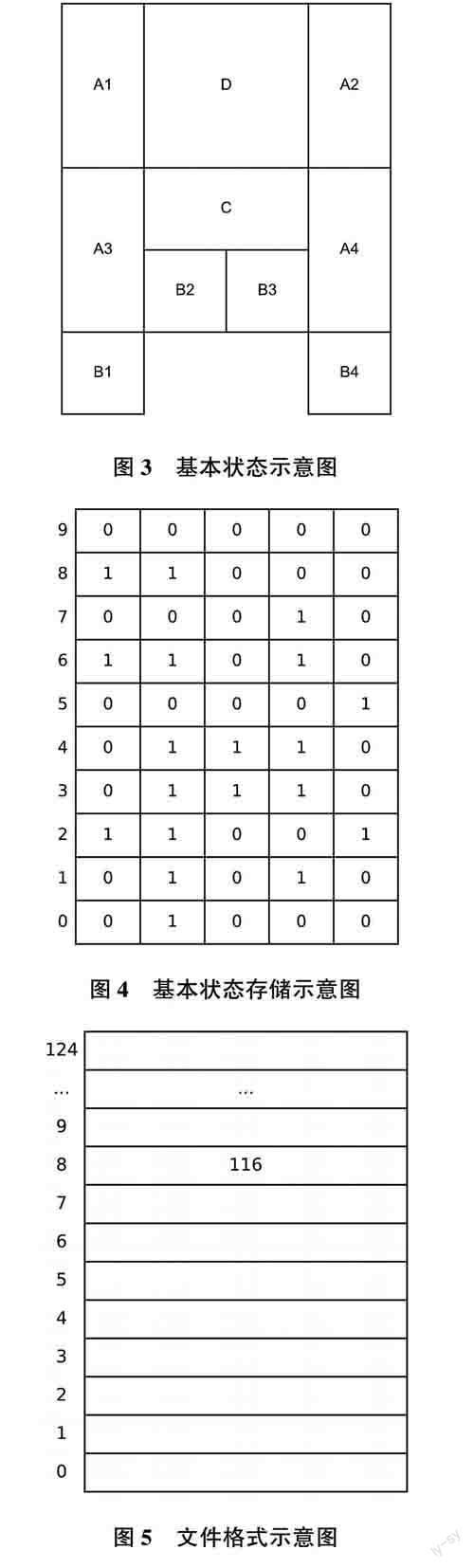
定義1狀態：10個棋子在棋盤的排列方式。

定義2棋盤坐標系：棋盤左上角為坐標原點D（0，0）；從坐標原點出發，水平向右為x軸正方向，長度為4；垂直向下為y軸正方向，長度為5，x與y為整數。

定義6狀態坐標：是一個長度為10的數組。第0～3個元素分別為趙云，馬超，張飛，黃忠；第4～7個元素分別為兵1，兵2，兵3，兵4；第8個元素為關羽；第9個元素是曹操。

定義7

基本狀態坐標：是一個長度為10的數組。第O—3個元素分別為4個1*2型棋子的坐標，順序記為AIA2A3A4；第4～7個元素分別為4個1*1型棋子的坐標，按順序記為BIB28384。其中，1*2型和1*1型棋子坐標按y從小到大的順序排列，若y相等，則再按x從小到大的順序排列。第8個元素為2*1型棋子的坐標，記為C：第9個元素是2*2型棋子的坐標，記為D。

圖1和圖2是兩個不同狀態，有不同的狀態坐標，但有相同的基本狀態坐標。

定義8

基本狀態：基本狀態坐標對應的狀態定義為基本狀態。

3枚舉所有合法狀態

3.1位置排列轉化為一維狀態坐標

根據一維棋子坐標的定義，d=0，20）。根據文獻[4]排列的定義及計算方法，從整數[0，20）取10個整數的排列共有P（20，10）種。每一種排列都是一個長度為10的數組，若將該種數組當作一個基本狀態坐標（數組中的每個數值對應一個一維棋子坐標），不考慮棋子重合的非法狀態，理論上共有P（20，10）=670442572800種狀態。

3.2合法狀態篩選

算法1

驗證狀態坐標是否合法

產生不合法狀態的原因是排列組合算法沒有考慮棋盤的形狀和棋子的形狀。比如，某個1*2型的棋子的坐標是（0，4），棋子就會超出棋盤范圍；若某個1*2型的棋子的坐標是（0，0），另外一個1*1型棋子的坐標是（1，0），這就會造成棋子重合。篩選合法狀態本質上是從所有狀態中去除超出棋盤范圍和棋子重合的情況，具體步驟如算法1所示。

4壓縮存儲

根據定義6和定義7．對于任意一個狀態坐標，都能求得其對應的基本狀態坐標。比如，記下“張飛”對應A1，那么可由基本狀態坐標還原成狀態坐標。基于這個事實，可以只存儲基本狀態坐標和其對應的最優解。對于基本狀態坐標，有A1～A4，B1～B4，C，D共10種棋子（圖3）。根據定義2，x軸的值為[0，4）的整數，y軸的值為[0，5）的整數，所以保存x軸的坐標需要2bit，保存v軸坐標需要3bit，保存一個棋子的坐標共需要5bit，10個棋子共需要50bit（圖4），即7個字節即可保存一個基本狀態坐標。但是，考慮到實際程序實現方便，用64位的整數（8字節）存儲基本狀態坐標。根據算法1，求得65880種合法狀態，對應65880個基本狀態坐標。

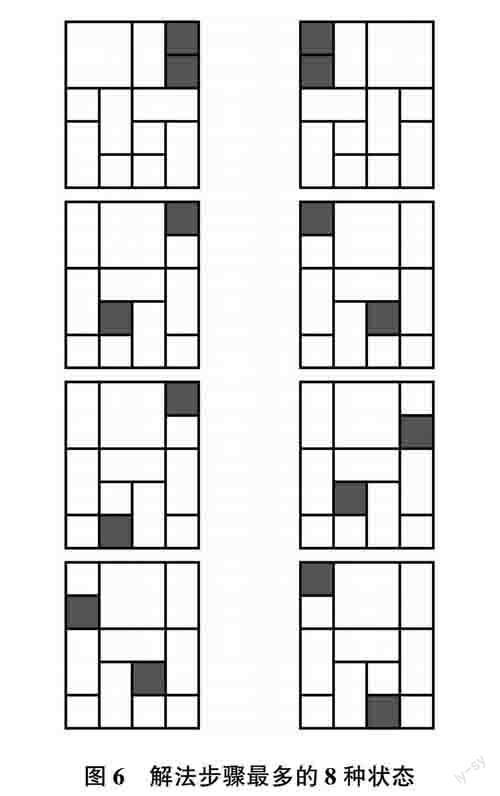
用改進的深度優先算法[5]，可得到53954種基本狀態有解。一個狀態占用8字節，存儲53954種約占421KB。由實驗結果可知．53954種有解的基本狀態中，最優解最多為126步，1字節就能表示。共有10個不同棋子，需要4bit表示，移動方向有上下左右4種，要2bit表示。因此，表示移動一步要用6bit。實驗部分為了實現方便，用1字節表示移動一步。如圖5所示，0—7個字節為基本狀態坐標。第8個字節為該基本狀態坐標的最優解有幾步。假定第8個字節為116，那么之后的116個字節表示116步具體內容。116個字節之后的8個字節又是下個基本狀態坐標，以此類推。如圖6所示。

5實驗

上文已經討論過華容道游戲共有P（20，10）種狀態，執行算法1后，得到65880種合法狀態。再執行文獻[5]的算法求得53954種基本狀態有解。用Python實現該過程，把基本狀態坐標及對應的最優解保存成第4節討論的二進制文件。結果表明，該文件僅2.8 MB。將該文件存人Python的字典（相當于hash表），用于求解最優解步數最多的8個狀態（圖6）。得到的結果如表1。表1第1列為基本狀態坐標，每個棋子的坐標用一維棋子坐標表示。第2列和第3列為運行時間對比。時間保留4位小數，單位是ms。文獻[5]是用C#實現的算法，C#是編譯型靜態語言。Python是動態語言，對于執行CPU密集型的算法，C#程序的效率要明顯高于Python。但是，同樣用Python實現文獻[5]和本文算法，在同樣的硬件上運行，在語言和硬件層面，兩個算法是公平的。由表1可知，基于hash表的算法尋找最優解的時間較短，個別小于0.001ms。從理論上分析，時間復雜度0（1）要低于0（V+E），所以表1的時間從理論上分析也是合理的。

6結束語

針對目前華容道算法的效率問題，利用排列算法求得華容道游戲所有可能的狀態，刪除不合法的狀態后，對每一種狀態求解，將每種狀態及最優解保存在hash表中。本質是將圖的遍歷算法轉化成查詢hash表，將時間復雜度由0（V+E）降為接近0（1）。理論分析和實驗結果表明，利用hash表解決華容道問題可以減少找到最優解的時間。