密度峰值聚類算法研究綜述

王森 邢帥杰 劉琛

摘要：密度峰值聚類（DPC）是一種新提出的基于密度和距離的聚類算法，由于其原理簡單，無需迭代和能處理形狀數據集等優點，正在數據挖掘領域得到廣泛應用。但DPC算法也有著一定的缺陷，如：對截斷距離參數敏感，初始聚類中心的選擇非自動化，后續標簽分配存在鏈式問題，時間復雜度較高等。文章對DPC算法的研究現狀進行了總結與整理，首先介紹了DPC的算法原理和流程;其次，針對DPC算法的不足對DPC算法的優化進行概括和分析，指出了優化算法的核心技術以及優缺點;最后，對DPC算法未來可能面對的挑戰和發展趨勢進行展望。

關鍵詞：聚類算法;密度峰值;截斷距離;初始聚類中心;微簇合并;時間復雜度

中圖分類號：TP391 文獻標志碼：A

本文引用格式：王森，邢帥杰，劉琛. 密度峰值聚類算法研究綜述[J]. 華東交通大學學報，2023，40（1）：106-116.

Survey of Density Peak Clustering Algorithm

Wang Sen， Xing Shuaijie， Liu Chen

（School of Science， East China Jiaotong University， Nanchang 330013， China）

Abstract：Density peak clustering（DPC） is a novel clustering algorithm based on density and distance. It is widely used in the field of data mining because of its simple principle， no iteration and the ability to process shape datasets. However， DPC algorithm also has some defects，including the sensitive cutoff distance parameter， non-automatic selection of initial clustering center， the chain problem in subsequent allocation and? high time complexity. This paper summarizes the research status of DPC algorithm. Firstly， it introduces the principle and process of DPC algorithm. Secondly， in view of the deficiencies of DPC algorithm， the optimization of DPC algorithm is summarized and analyzed， and the core technology， advantages and disadvantages of the optimization algorithm are pointed out. Finally， the possible challenges and development trend of DPC algorithm in the future are concluded.

Key words： clustering algorithm; density peak; cutoff distance; initial cluster center; micro-cluster merge; time complexity

Citation format：WANG S，XING S J，LIU C. Survey of density peak clustering algorithm[J]. Journal of East China Jiaotong University，2023，40（1）：106-116.

隨著互聯網和信息技術的快速發展，數據量每天都在以驚人的速度增加，人類社會已步入大數據時代，如何從海量數據中挖掘潛在的有價值的信息是一個迫切的問題。聚類分析是數據挖掘和機器學習領域一種處理大數據的重要方法，無需先驗知識[1]。其主要目的是根據數據集的某些特征將數據集劃分為幾個不同的潛在的簇，并且使簇內數據對象的相似性盡可能高，簇間的相似性盡可能低[2]。各種聚類算法已經成功應用于許多領域，如：圖像處理[3-4]、短文本聚類[5]、損傷診斷[6]、模式識別[7]、生物信息學[8]、信息檢索[9]等。

目前得到廣泛使用的聚類算法非常多，并且研究人員仍在尋找新的聚類算法以應對各種不同的聚類任務。在過去的幾十年里，涌現出了許多不同類型的聚類算法，主要包括基于劃分的K-Means[10]和K-Medoid[11]算法，基于密度的DBSCAN[12]和OPTICS[13]算法，基于層次的CURE[14]和BIRCH[15]算法，基于網格的方法[16]，基于圖論的方法[17]，基于模型的方法[18]以及基于深度學習的方法[19]等。

2014年，Rodriguez和Laio[20]在SCIENCE提出了一個基于密度和相對距離的新算法（clustering by fast search and find of density peaks，DPC）。其主要基于兩個假設：① 聚類簇的中心的密度要比其周圍數據對象的密度高;② 聚類中心到比它密度更高的數據對象的距離較遠。由于DPC算法可解釋性強，無需迭代，算法簡單且能處理不同類型的數據集而備受矚目。但DPC算法也有著一定的局限性，比如截斷距離參數的選取需要提前確定，初始聚類中心的確定受人為主觀影響，后續標簽分配的鏈式問題，算法的復雜度較高等。為了提高DPC的性能以及克服上述缺點，各個領域的學者已經做了很多工作并提出了一系列的優化算法。

本文首先簡述傳統DPC算法的原理以及算法流程，然后針對DPC算法的不足，按照4個優化方向分類討論了不同優化算法的關鍵技術與優缺點，最后對DPC算法的未來發展所可能面臨的挑戰及優化方向進行了展望。

1 傳統密度峰值聚類算法

1.1 密度峰值聚類算法原理

DPC算法是一種基于距離和密度的無監督的聚類算法，且無需提前輸入簇的真實個數。DPC算法首先尋找密度峰值點作為初始聚類中心，之后按照距離將剩余非中心點分配至最近的聚類中心所在的簇。尋找簇中心（密度峰值點）作為算法最重要的一步，主要思想基于兩個假設：① 簇的中心局部密度較高且被密度比它低的數據所包圍;② 簇中心到比其密度更大的數據對象的距離相對較大。針對以上假設，DPC的作者提出了兩個重要參數描述每一個數據對象：局部密度ρ和與密度更高點的相對距離δ。

對于數據集X={x1，x2，…xn}，采用歐式距離計算兩點之間的相似性

dist（xi，xj）= （1）

式中：m為數據的維度;xil是數據對象xi在第l個維度下的取值。

DPC算法使用截斷距離dc或者高斯核計算數據對象的局部密度ρi，對于數據集X每一個數據對象xi，其局部密度ρi的計算為

ρi=φ（dist（xi，xj）-dc） （2）

式中：φ（x）為判斷函數，當x≥0時，φ（x）=1;當x<0時，φ（x）=0。

ρi=exp-

（3）

式中：dist（xi，xj）表示數據對象xi和xj之間的歐氏距離，dc>0。式（2）計算的局部密度即為以數據對象xi為中心，以截斷距離dc為半徑的鄰域內包含的點的個數，或者可以認為是與數據對象xi的距離小于dc的數據對象的個數。式（3）計算的則是所有數據對象到該點的高斯距離之和。

相對距離δi定義為

δi=（dist（xi，xj））? ? ?（4）

對于具有最大局部密度的數據對象，其相對距離δi為

δi=（δj）? （5）

DPC算法認為，當局部密度ρ和相對距離δ的值都比較大時，此時對應的數據對象即為初始聚類中心（密度峰值點）。通過繪制出關于ρ和δ的二維決策圖，初始聚類中心點與非聚類中心點明顯分開，故通過人為選擇位于右上角區域（較大的ρ和δ）的點作為初始聚類中心點，且挑選出的點的個數即為最終聚類簇的個數。圖1（a）為數據實際分布情況，圖1（b）為投影至二維空間得到的決策圖。密度峰值點即為決策圖右上角的突出的點1和點10，參考圖1（a），這兩點位于每一個簇的中心位置，表明選擇的初始聚類中心是合適的。點7雖然也有較高的密度，但其相對距離δ的值很小，這說明在點7的周圍存在密度比其更大的點（點1），點7不能作為初始聚類中心。另外點28具有較高的值但密度較小，這表明點28是遠離聚類簇的噪聲點。

另外也可以通過決策值γi=ρi δi選擇聚類中心，選擇具有較大決策值的點作為初始聚類中心。最后再將所有的非聚類中心點分配至距離最近的聚類中心點所在的簇中，完成聚類過程。

1.2 傳統DPC算法流程

密度峰值聚類算法的主要步驟如下：

1） 輸入數據集X={x1，x2，…，xn};

2） 根據式（1）計算n個數據對象之間的歐式距離矩陣Dn×n;

3） 根據式（2）或（3）計算數據對象局部密度參數ρi;

4） 根據式（4）或（5）計算數據對象xi到具有更高密度的數據點的最近距離δi;

5） 根據密度參數ρi和相對距離參數δi繪制決策圖;

6） 根據決策圖或決策值γ挑選合適的初始聚類中心;

7） 將剩下的非聚類中心點分配至具有更高的密度ρi中距離最近的點所在的簇;

8） 輸出最終聚類結果φ={C1，C2，…，Cm}。

2 密度峰值聚類算法的優化

2.1 實現DPC算法的自動化

提前確定合適的截斷距離參數與密度峰值點的選取阻礙了算法的自動化。DPC算法的核心即尋找密度峰值點，而決定密度參數大小的因素主要取決于dc。DPC算法對輸入dc的值異常敏感，過大或者過小的dc值可能產生完全不同的聚類結果，聚類精度波動大，但提前確定合適的dc的值是非常困難的。另外，密度峰值點的選取是人為通過決策圖選取的，當決策圖復雜時難以選取合適的峰值點，且操作人員得到的峰值點受主觀影響較大，同一個數據集可能會產生不同的選擇結果。

Liu等[21]在ADPC-KNN中引入K-最近鄰的思想自動計算截斷距離dc以及基于K-最近鄰的密度ρi計算方式

ρi=exp（）? ? （6）

dc=μK+? ? ?（7）

μK=δiK? ? ? （8）

式中：dij為兩點間的歐氏距離;δiK為數據點i與第K個最近鄰之間的距離;N為整個數據集的容量;μk為不同數據點的δik的均值。ADPC-KNN能自適應地找到合適的dc值和初始聚類中心。雖然算法減少了對dc的依賴性，但同時引入了需要提前確定的K-最近鄰參數。另外，算法仍然需要通過人工確定初始聚類中心的個數。

王芙銀等[22]提出一種結合鯨魚優化算法的WOA-DPC算法，建立ACC目標函數，利用鯨魚優化算法迭代尋找使指標最大時所對應的dc值即最優的截斷距離參數。另外，根據加權的決策值斜率的變化情況確定初始聚類中心。該算法實現了自動化，降低了對截斷參數的依賴性。但WOA-DPC算法的時間復雜度高于傳統DPC算法，在針對大型數據集時耗時較長。

Wang等[23]引入物理學中的數據場的勢能熵，自動確定計算密度參數時的截斷參數dc，避免了人為確定的隨機性。場函數中數據對象的潛在勢能φi即數據分布的局部密度，越密集的對象φi的值越大，能很好地反應數據分布的情況。熵用來描述數據集的不穩定性，最小的熵取值對應于σ的最優取值。最后根據高斯分布的3σ準則，得到最優dc的值為σ。實驗結果表明，針對小型數據集，該算法的聚類效果優于傳統算法且能自動確定截斷參數dc的取值，但面對大型數據集時的有效性還有待研究。

王洋等[24]引入基尼指數描述數據的不純度，自適應地確定截斷距離參數dc同時自動獲取初始聚類峰值點。當基尼指數的值最小時所對應的σ的取值即為截斷距離參數dc。按γ對數據點降序排列，并繪制二維圖像，橫坐標為數據點的排列序號，縱坐標為γ值。然后通過尋找決策值的臨界值p自動選擇初始聚類中心，如果p滿足

p=max{i | ki-ki+1≥β，i=1，2，3，…，n-2}? （9）

β=a（j）/（n-2）? ? （10）

a（j）=kj-kj+1? ? ?（11）

式中：ki為γ排序圖上相鄰兩點之間的斜率;a（j）為γ序列圖中相鄰兩點之間斜率差的和，β為數據集中a（j）的平均值。

Flores等[25]提出一種通過檢測決策值γ在連續數據點之間的差距gap進而自動確定聚類中心的方法。首先將所有數據對象{x1，x2，…，xn}按照γ值降序排列為P={p1，p2，…，pn}。并定義點距離di=

γi+γi+1，平均點距離為d=，則最后一次出現的di≥d所對應的點i即為閾值點，比點xi的γ值大的數據點將被自動視為初始中心。

Ding等[26]提出新的判斷初始聚類中心的參數，提出了DPC-GEV和DPC-CI自動選擇初始聚類中心。首先采用“最小最大化”將局部密度ρ和相對距離δ標準化，DPC-GEV認為新的判斷參數θ=min（ρ*，δ*）大致遵循廣義極值分布，利用式（12）確定分位數p，θ>p的點被視為初始中心。

p=

-

（1-yp-ξ），

≠0

-

log yp，

≠0 （12）

yp=-log p? ? ? （13）

式中：，，的值均通過最大似然估計確定。DPC-CI借助切比雪夫不等式，如果點i滿足式（14）則被視為初始聚類中心。

θi>（μ+ε×σ），?ε>0 （14）

式中：μ和σ分別為判斷指標θ的均值和標準差。實驗結果表明，DPC-GEV與DPC-CI可以選擇出合理的初始中心，保證了DPC的連續性。但由于新的判斷指標θ需參考局部密度參數，對于截斷參數dc的依賴仍然存在。

關于上述DPC自動化的優化策略的對比分析如表 1 所示。

2.2 優化密度參數ρ和相對距離δ

盡管DPC算法能處理大部分形狀數據集，但局部密度的定義過于簡單，當面對形狀結構復雜的數據集時聚類精度下降。例如一個簇內存在多個密度峰會導致簇被分割，數據分布的稠密性差異較大時DPC會忽視稀疏簇，流形數據集中位于不同簇但距離較近的數據對象被誤分配標簽等。需要對DPC算法中的密度ρ和相對距離δ進行優化以適應不同類型的數據集。

Guo等[27]提出的NDPC認為無論是在密集或者稀疏的簇中，相比于其他點，聚類中心被包含在更多的K-最近鄰中。將數據對象的局部密度定義為其鄰居包含該點的數據對象的個數，從而公平對待密度分布差異較大的區域。基于此定義，初始聚類中心的挑選不會造成稀疏簇的遺漏。另外，若一個簇中存在多個密度峰值，提出NDPC結合凝聚層次聚類算法的NDPC-AC將被分割的小簇迭代合并，直到最終簇的個數等于真實簇的個數，但NDPC-AC算法的凝聚策略需要提前知道真實簇的個數。劉娟等[28]提出一種借助自然反向最近鄰的密度峰值聚類算法，利用反向最近鄰計算密度參數，利用密度自適應距離計算初始中心的距離，之后挑選更為合適的初始聚類中心（密度峰值點）。Du等[29]提出的DPC-KNN-PCA中將K-最近鄰的思想引入密度峰值聚類算法并改進局部密度的定義，同時結合主成分分析（PCA）降維處理高維數據。

Hou等[30]認為造成DPC算法性能不佳的原因是算法假設與實現過程的不一致性。假設基于數據對象間的相對密度關系，而算法實施過程中密度參數的計算卻是絕對密度關系，故作者提出了一個新的基于相對密度關系的初始聚類中心識別準則。首先，作者提出從屬點和直接上級點的定義，并認為數據點與其上級點存在于同一個簇中。如圖2所示，箭頭由從屬點指向直接上級點。

如果x2是x1最近的高密度點，即δ1=d（x1，x2），那么x1是x2的直接從屬點，x2是x1的直接上級點。為防止兩個獨立簇的合并，滿足δ>T的點被視為聚類中心，聚類中心點不會作為任意點的從屬點。其次，數據對象x1的局部密度ρi′通過只考慮直接從屬點的個數ηi確定

ρi′=ζ（si，xj）? ? （15）

ζ（u，v）=1， v為u的直接從屬點且v∈

S

0， 其他 （16）

式中：S代表數據點xi的ηi最近鄰的集合。該算法在數據密度分布不均勻時的聚類效果優于其余聚類算法，但閾值T和初始聚類中心仍需要人為提前指定，且算法結果受K-最近鄰參數K的影響較大。

Xu等[31]提出的RDPC-DSS在DPC算法中用密度自適應距離代替歐式距離處理流形數據集。在流形數據集中，如果兩點可以通過一條穿過高密度區域的路徑連接，那么稱他們具有較高的相似度。數據集X={x1，x2，…，xn}中的數據對象可以被視為圖G=（V，E）的結點，P={p1，p2，…，pl}為p1至pl的路徑，pij為連接v1至v2的所有路徑。密度自適應距離Sij的計算為

Sij= （17）

式中：ρ′為放縮因子。之后將密度自適應距離引入DPC算法，更新局部密度和相對距離的定義。RDPC-DSS在流形數據集上的聚類效果優異，但計算密度自適應距離的時間復雜度遠高于DPC算法，使得處理大型數據集需要消耗大量的時間。

Lotfi等[32]提出的DPC-DBFN根據一種新的模糊核進行局部密度的計算，減少離群點的影響。根據決策圖篩選出簇主干，簇主干能大致保持數據集的形狀且距另一簇的主干距離較遠，然后完成對剩余非主干點標簽的傳播。

第1步，基于模糊鄰域的密度參數ρi定義為

ρi=max1-

dxi，xj，0? ? （18）

式中：KNN（xi）為數據點xi的K-最近鄰。

第2步根據決策圖確定聚類中心點，簇主干點，邊界點以及噪聲點。score函數值最大的c個數據作為初始聚類中心

score（i）=

2×? ? （19）

對于其余數據，如果ρi>ρ，則xi為主干中的密集點;如果ρi<ρ且δi<λσδ2，則xi為簇的邊界點;如果ρi<ρ且δi<λσδ2，則xi為噪聲點。其中，λ為控制參數，σδ2為相對距離的方差。

第3步分配標簽主要包括主干點的分配以及邊界點的分配。標簽分配過程始于將簇中心的標簽分配到附近的主干點，首先將每個簇的標簽傳給初始中心的K個最近的主干鄰居，之后再將標簽傳遞給鄰居的鄰居，重復此過程，直到所有主干密集點都被分配簇標簽。DPC-DBFN成功地克服了初始DPC算法以及大部分優化算法帶來的問題，該算法能有效地識別聚類中心，并且能對形狀復雜的數據進行聚類，并且對于噪聲點具有魯棒性。但該算法中仍存在兩個參數需要確定，控制參數和最近鄰參數K，且其對于聚類性能有著較大的影響。

基于共享最近鄰的快速搜索密度峰值聚類算法SNN-DPC[33]提出了共享最近鄰的概念，充分考慮數據集的結構和形狀提出了新的兩個數據對象的相似性度量。并采用補償值的方式來處理簇間密度差異較大的數據集，為改善DPC算法后續非中心點分配過程的鏈式問題，提出了兩步分配的策略。共享最近鄰SNN定義為K-最近鄰的交集SNN，基于SNN的相似性sim（xi，xj）定義為

sim（xi，xj）=，

若xi，xj∈SNN（xi，xj）

0，? ? ? ? ? ? ? ? 其他 （20）

式中：局部密度ρ定義為具有最大SNN相似性的K個數據對象的相似性之和。當數據分布的稀疏程度差異較大時，為避免忽視稀疏簇，提出基于補償值的相對距離δ的定義。SNN-DPC在面對復雜形狀數據集時取得了優異的聚類結果，且對噪聲點具有魯棒性。但缺點在于需要提前確定K-最近鄰的參數K，以及初始聚類中心仍需要通過人工選取，打斷了算法的連續性。

本小節基于DPC優化密度參數和相對距離的不同策略，分析了優化算法的核心技術以及優缺點，優化算法的對比分析如表 2 所示。

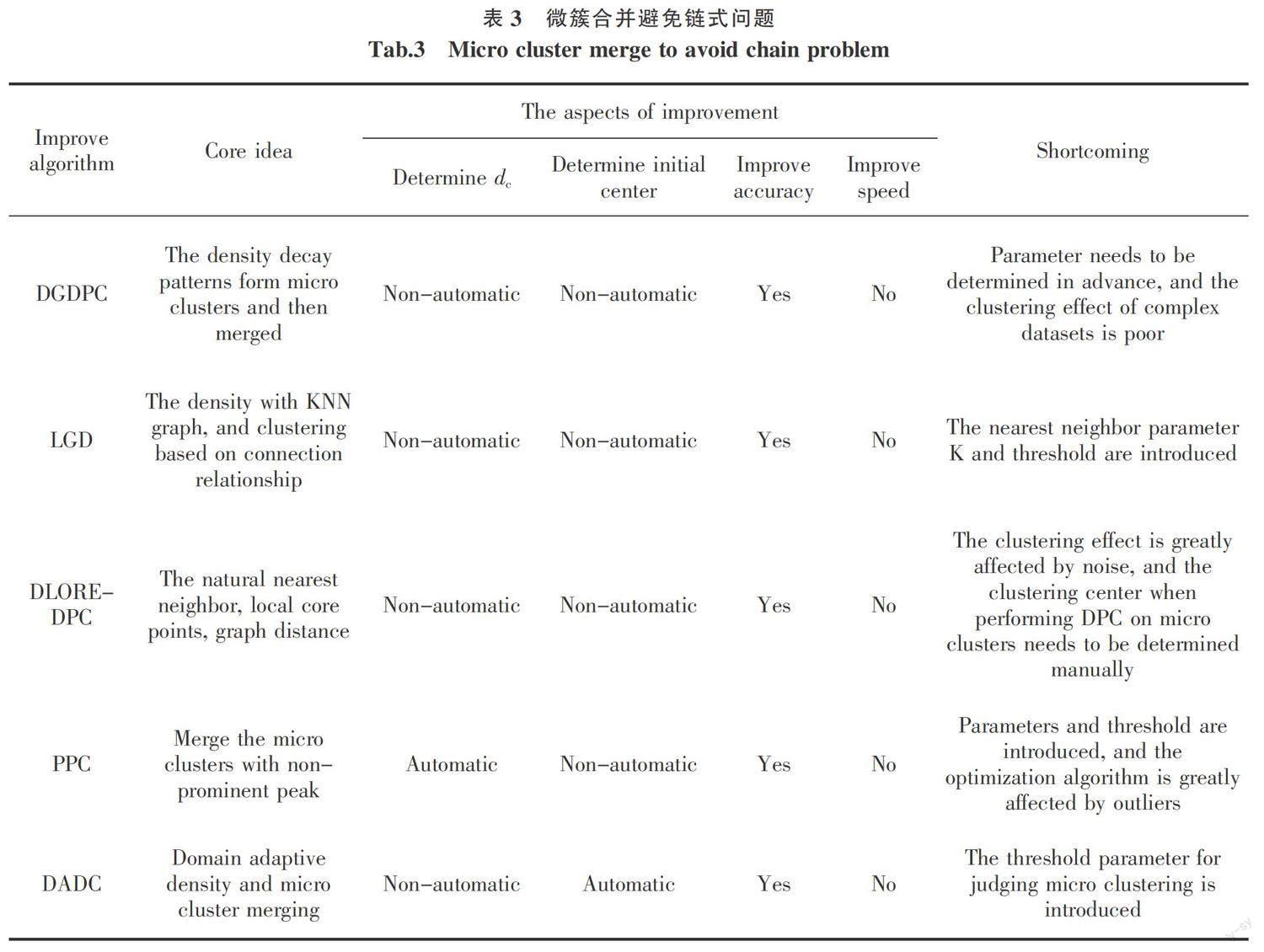
2.3 微簇合并避免鏈式問題

DPC算法在面對流形數據集時，受算法假設的影響，即使挑選了合適的初始聚類中心，但在后續非中心點標簽的分配過程中可能會產生鏈式問題：一個誤分配點可能會導致大范圍數據標簽的錯誤傳播。凝聚層次聚類算法將數據對象看作單獨簇，每次合并相似度最高的兩個簇，直至合并到真實簇的個數。研究人員提出了一些類似于層次聚類的算法，先將數據集劃分成多個微簇，對數據對象進行局部范圍內的標簽的分配，避免鏈式問題。微簇的個數往往大于真實簇的個數，之后根據提出的簇間相似性不斷地將微簇進行合并以形成最終的聚類結果。

Zhang等[34]受自然界衰減現象的啟發，提出基于密度衰減圖的DGDPC算法，通過密度衰減圖形成初始簇，之后根據同一衰減現象下的數據對象屬于同一個簇完成聚類過程。Li等[35]定義一種局部密度差異處理高維且數據分布不均勻的數據集，考慮了數據對象與其鄰居的密度差異，公平對待稠密程度不同簇的確定核心點。之后在K最近鄰圖上尋找潛在的交叉簇的邊，并刪除連接了噪聲的邊以及距離過遠的邊，最后根據得到的新的K-最近鄰圖完成聚類。Bie等[36]提出了Fuzzy-CFSFDP算法借助模糊規則對不同的密度峰挑選不同的聚類中心，并且將具有相近的內部模式的密度峰進行合并，最后通過一種啟發式的方式挑選合適的初始中心。

Cheng等[37]將自然最近鄰的概念引入密度峰值聚類算法，提出了一種無需參數的基于局部核心密集成員的DLORE-DPC算法，其本質是先尋找微簇核心再進行微簇間的合并。通過挑選局部核心代表整個數據集，形成不同的微簇核心，之后在局部核心點之上通過圖距離完成DPC，最后根據代表點完成對剩余點的標簽的分配。數據點xi局部密度den（xi）為

den（xi）=? ? ?（21）

式中：k為xi的自然最近鄰數。如果數據對象p是q的局部鄰域里具有最大den的點，則p稱作數據對象q的代表點，記作REP（q）=p。在此基礎上，如果REP（p）=p，數據對象p被認為是一個局部核心點。將局部核心點的集合視為一個較小數據集，對其執行DPC算法，兩個局部核心點p，q之間基于圖的距離DG（p，q）定義為

DG（p，q）=DS（pk，pk+1）? ?（22）

DS（p，q）=

，

若SNN（p，q）≠0

maxd，? ? ? ? ? ? ? ? 其他（23）

式中：pk，pk+1為最短路徑上相鄰的局部核心點;m為連接核心點的節點數;dlsore（p，q）為局部核心點之間的共享最近鄰。實驗結果表明，DLORE-DPC算法無需人為輸入參數能發現不同形狀的聚類簇，由于該算法只計算局部核心之間的圖距離且只對核心點執行DPC算法，算法的時間復雜度得到大大降低，但自然最近鄰搜索算法受噪聲點的影響較大且核心點集上的初始聚類中心的選取仍未自動化。

Ni等[38]提出了一種尋找突出峰值點的優化算法PPC，其通過將數據集劃分為多個潛在的簇，然后將密度峰值不突出的簇合并，從而獲得準確的聚類結果。首先根據統計學中標準差和均值可以衡量數據的中心化趨勢，將滿足δi>δ+S的數據點視為潛在的簇中心，δ和S分別代表相對距離參數的均值和標準差，此時得到的簇的個數多于真正簇的個數。然后使用兩個密度峰之間的密度差確定峰值是否突出。如果此峰的密度差異大于閾值th，則足夠突出，就是一個聚集中心;否則，它與密度較高的鄰近峰在同一簇中。

Chen等[39]認為對于具有變密度分布（VDD）數據集，繼續使用統一的密度函數會導致稀疏簇的丟失，故提出了針對數據密度分布不均勻的優化算法DADC。首先定義了一種基于K-最近鄰（KNN）的區域自適應密度，以自適應地檢測不同密度區域的密度峰值。區域自適應密度ρi定義為

ρi=i×

i=max

i×

（dij），其他? ? （24）

i=denk（i）+j∈K（（j）（denk（j）×ωi）? ? （25）

denk（i）=? ? （26）

其中：ωi=1/dij為數據與其K-最近鄰的權重值;denk（i），denk（j）為中間變量。最后根據簇間融合度是否大于閾值決定微簇的合并。

基于微簇合并避免鏈式問題的優化DPC算法的對比分析如表3所示。

2.4 提升算法速度

DPC算法的時間復雜度較高，DPC算法的時間復雜度主要由三方面組成：第一，計算數據點之間的歐氏距離矩陣需要消耗O（N2）;第二，對于每個數據對象的局部密度和相對距離的計算都需要遍歷數據集中的每一個點，時間復雜度為O（N2）;第三，對于非聚類中心點的分配過程的時間復雜度為O（N2）。因此，DPC算法整體的時間復雜度為O（N2），算法的時間消耗較大，處理大型數據集時的效率不高。

Chen等[40]提出的FastDPeak算法基于降低原始DPC算法中計算局部密度和對距離的時間復雜度。首先采用Cover-tree尋找每個數據對象的K-最近鄰，并利用KNN密度代替原始密度。其次對于相對距離的計算，將數據對象分為局部密度峰值和一般點（非局部密度峰值）。局部密度峰值點是數據對象在其K-最近鄰具有最大的局部密度，否則為一般點。一般數據點的相對距離的計算只需要遍歷其K-最近鄰，而對于局部峰值點，通過逐漸擴大K值的方式計算其相對距離，大大降低了算法計算密度的時間消耗，時間復雜度約為。Wu等[41]提出了DGB聚類算法，DGB運用了網格化的思想減少數據空間中不必要的歐式距離的計算。首先將數據空間進行網格化得到一些小單元格Cell，將原本每個數據點之間的歐氏距離替換為計算少量的非空單元格Cell之間的距離，這大大地提升了算法的計算速度。Sami等[42]提出一種優化的快速密度峰值聚類算法FastDP，在對聚類質量沒有明顯影響的情況下實現了算法的加速。其使用一種快速且通用性強的K-最近鄰圖計算局部密度和相對距離參數，傳統DPC算法二次時間復雜度的問題得到消除，并允許對大規模的數據集進行聚類。

表4對比分析了基于提升速度的優化DPC算法。

3 結束語

本文主要將DPC的優化算法基于4大類進行了詳細闡述和分析：實現DPC的自動化，優化密度參數和相對距離，微簇合并避免鏈式問題與提升算法速度，并指出優化算法的核心技術及優缺點。

參考文獻：

[1] XU R，WUNSCH D. Survey of clustering algorithms[J]. IEEE

Transactions on Neural Networks，2005，16（3）：645-678.

[2] JAIN A K，Murty M N，FLYNN P J. Data clustering：a review[J]. ACM Computing Surveys（CSUR），1999，31（3）：264-323.

[3] HOU J，LIU W，XU E，et al. Towards parameter-independent data clustering and image segmentation[J]. Pattern Recognition，2016，60：25-36.

[4] SULAIMAN S N，ISA N A M. Adaptive fuzzy-K-means clustering algorithm for image segmentation[J]. IEEE Transactions on Consumer Electronics，2010，56（4）：2661-2668.

[5] YIN J，WANG J. A dirichlet multinomial mixture modelbased approach for short text clustering[C]//Association for Computing Machinery：Proceedings of the 20th ACM SIGKDD international conference on knowledge discovery and data mining，2014.

[6] 韓慶華，馬乾，劉名，等. 溫度變化下基于固有頻率聚類分析的空間網格結構損傷診斷[J]. 華東交通大學學報，2021，

38（4）：8-17.

HAN Q H，MA Q，LIU M，et al. Damage diagnosis of space grid structure based on natural frequency clustering analysis under varying temperature effects[J]. Journal of East China Jiaotong University，2021，38（4）：8-17.

[7] HAMZA A B. Graph regularized sparse coding for 3D shape clustering[J]. Knowledge-Based Systems，2016，92：92-103.

[8] TRUONG H Q，NGO L T，PEDRYCZ W. Granular fuzzy possibilistic C-means clustering approach to DNA microarray problem[J]. Knowledge Based Systems，2017，133：53-65.

[9] BORDOGNA G，PASI G. A quality driven hierarchical data divisive soft clustering for information retrieval[J]. Knowledge-

based systems，2012，26：9-19.

[10] MACQUEEN J. Some methods for classification and analysis of multivariate observations[C]//Berkelay：Proceedings of the fifth Berkeley symposium on mathematical statistics and probability. 1967，1（14）：281-297.

[11] KAUFMAN L，ROUSSEEUEW P J. Finding groups in data：an introduction to cluster analysis[M]. London：John

Wiley & Sons，2009.

[12] ESTER M，KRIEGEL H P，SANDER J，et al. A density-based algorithm for discovering clusters in large spatial databases with noise[J]. Data Base System and Logic，1996，

96（34）：226-231.

[13] ANKERST M，BREUNIG M M，KRIEGEL H P，et al. OPTICS：Ordering points to identify the clustering structure[J]. ACM Sigmod Record，1999，28（2）：49-60.

[14] GUHA S，RASTOGI R，SHIM K. CURE：An efficient clustering algorithm for large databases[J]. ACM Sigmod Record，1998，27（2）：73-84.

[15] ZHANG T，RAMAKRISHNAN R，LIVNY M. BIRCH：an efficient data clustering method for very large databases[J]. ACM Sigmod Record，1996，25（2）：103-114.

[16] WANG W，YANG J，MUNTZ R. STING：A statistical information grid approach to spatial data mining[J]. Programming，1997，97：186-195.

[17] VON L U. A tutorial on spectral clustering[J]. Statistics

and Computing，2007，17（4）：395-416.

[18] DEMPSTER A P，LAIRD N M，RUBIN D B. Maximum likelihood from incomplete data via the EM algorithm[J].

Journal of the Royal Statistical Society：Series B（Methodological），1977，39（1）：1-22.

[19] 章永來，周耀鑒. 聚類算法綜述[J]. 計算機應用，2019，

39（7）：1869-1882.

ZHANG Y L，ZHOU Y J. Review of clustering algorithms[J]. Journal of Computer Applications，2019，39（7）：1869-1882.

[20] RODRIGUEZ A，LAIO A. Clustering by fast search and find of density peaks[J]. Science，2014，344（6191）：1492-1496.

[21] LIU Y H，MENG E M，YANG F. Adaptive density peak clustering based on K-nearest neighbors with aggregating strategy[J]. Knowledge-Based Systems，2017，133：208-220.

[22] 王芙銀，張德生，張曉. 結合鯨魚優化算法的自適應密度峰值聚類算法[J]. 計算機工程與應用，2021，57（3）：94-102.

WANG F Y，ZHANG D S，ZHANG X. Adaptive density peaks clustering algorithm combining with whale optimization algorithm[J]. Computer Engineering and Applications，2021，57（3）：94-102.

[23] WANG S，WANG D，LI C，et al. Clustering by fast search and find of density peaks with data field[J]. Chinese Journal

of Electronics，2016，25（3）：397-402.

[24] 王洋，張桂珠. 自動確定聚類中心的密度峰值算法[J]. 計算機工程與應用，2018，54（8）：137-142.

WANG Y，ZHANG G Z. Automatically determine density of cluster center of peak algorithm[J]. Computer Engineering and Applications，2018，54（8）：137-142.

[25] FLORES K G，GARZA S E. Density peaks clustering with gap-based automatic center detection[J]. Knowledge Based

Systems，2020，206：106350.

[26] DING J，HE X，YUAN J，et al. Automatic clustering based on density peak detection using generalized extreme value distribution[J]. Soft Computing，2018，22（9）：2777-2796.

[27] GUO Z，HUANG T，CAI Z，et al. A new local density for density peak clustering[C]//Springer Cham：Pacific-Asia Conference on Knowledge Discovery and Data Mining，2018.

[28] 劉娟，萬靜. 自然反向最近鄰優化的密度峰值聚類算法[J]. 計算機科學與探索，2021，15（10）：1888-1899.

LIU J，WAN J. Optimized density peak clustering algorithm by natural reverse nearest neighbor[J]. Journal of Frontiers of Computer Science and Technology，2021，15（10）：1888-1899.

[29] DU M，Ding S，JIA H. Study on density peaks clustering based on K-nearest neighbors and principal component analysis[J]. Knowledge-Based Systems，2016，99：135-145.

[30] HOU J，ZHANG A，QI N. Density peak clustering based on relative density relationship[J]. Pattern Recognition，2020，

108：107554.

[31] XU X，DING S，WANG L，et al. A robust density peaks clustering algorithm with density-sensitive similarity[J].

Knowledge-Based Systems，2020，200：106028.

[32] LOTFI A，MORADI P，BEIGY H. Density peaks clustering based on density backbone and fuzzy neighborhood[J].

Pattern Recognition，2020，107：107449.

[33] LIU R，WANG H，YU X. Shared-nearest-neighbor-based clustering by fast search and find of density peaks[J]. Information Sciences，2018，450：200-226.

[34] ZHANG Z，ZHU Q，ZHU F，et al. Density decay graph-based density peak clustering[J]. Knowledge Based Systems，2021，224：107075.

[35] LI R，YANG X，QIN X，et al. Local gap density for clustering high-dimensional data with varying densities[J].

Knowledge Based Systems，2019，184：104905.

[36] BIE R，MEHMOOD R，RUAN S，et al. Adaptive fuzzy

clustering by fast search and find of density peaks[J]. Personal and Ubiquitous Computing，2016，20（5）：785-793.

[37] CHENG D，ZHANG S，HUANG J. Dense members of local cores based density peaks clustering algorithm[J]. Knowledge Based Systems，2020，193：105454.

[38] NI L，LUO W，ZHU W，et al. Clustering by finding prominent peaks in density space[J]. Engineering Applications of Artificial Intelligence，2019，85：727-739.

[39] CHEN J，PHILIP S Y. A domain adaptive density clustering algorithm for data with varying density distribution[J]. IEEE Transactions on Knowledge and Data Engineering，2019，33（6）：2310-2321.

[40] CHEN Y，HU X，FAN W，et al. Fast density peak clustering for large scale data based on KNN[J]. Knowledge Based Systems，2020，187：104824.

[41] WU B，WILAMOWSKI B M. A fast density and grid based clustering method for data with arbitrary shapes and noise[J]. IEEE Transactions on Industrial Informatics，2016，13（4）：1620-1628.

[42] SIERANOJA S，FRANTI P. Fast and general density peaks clustering[J]. Pattern Recognition Letters，2019，128：551-

558.