多孔介質中Brinkman方程組解的連續依賴性*

石金誠

廣州華商學院數據科學學院，廣東 廣州 511300

Straughan et al.（1999）引入了具有Soret 效應且不可壓縮的對流擴散Brinkman 方程，他們在有界區域內建立了解對Soret 系數的連續依賴性，有關Brinkman 方程更系統的介紹見文獻（Nield et al.，1992；Straughan，2008）。偏微分方程（組）的連續依賴性或收斂性，稱之為結構穩定性，關于結構穩定性的本質見文獻（Ames et al.，1997）。

近年來，多孔介質中流體方程組的研究越來越受到學者們的關注，其中較為典型的流體方程組有Brinkman、Darcy 和Forchheimer 方程組，文獻（Payne et al.，2007）討論了這些方程組的Saint-Venant 原理。文獻（Franchi et al.，2003；Lin et al.，2007；Ciarletta et al.，2015；Cichon et al.2015；Chen et al.，2016；Liu，2017；Liu et al.，2018a；Liu et al.，2018b；李遠飛，2019a；李遠飛，2019b；李遠飛等，2019；李遠飛，2020）討論了包括Brinkman、Darcy 和Forchheimer 方程組在內更多偏微分方程組的結構穩定性，獲得了一些新的成果。本文我們考慮如下Brinkman方程組

其中ui，p，T，C分別為速度、壓強、溫度和鹽濃度，gi(x)和hi(x)為重力函數且|gi|，|hi|≤1，?為拉普拉斯算子，σ> 0是Soret系數，λ> 0是Brinkman系數。

方程組（1）在Ω ×[0，τ]內成立，其中Ω 是R3中有界單連通的凸區域，τ是固定的一個常數且0 ≤τ< +∞.我們所考慮的溫度與鹽濃度的邊界是絕緣的，并且溶質通過邊界的通量為0。其邊界條件為

此外，初始條件為

本文研究了方程組（1）的解對Brinkman系數λ的連續依賴性。為了獲得連續依賴性的結果，通常的做法是利用溫度和鹽濃度的最大值，去推導出交叉項的先驗界，而本文方程組（1）的第4 個方程中含有溫度的拉普拉斯項，該項的存在導致鹽濃度C的最大值估計難度很大。為了克服這個難題，我們采用給出C的四階范數的先驗界。為了推導出到C的四階范數的先驗界而構造的函數是文中最大創新點。

1 先驗估計

本節中將給出在后面定理的證明中所需的若干估計。

引理1 對于溫度T，我們有如下估計

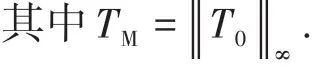
證明在方程組(1)的第3個方程兩邊同時乘以T2p?1，p≥1，并在Ω上積分得

且式（5）化為

即證明了式（3）。

在式（6）中取p= 1，有

則

證畢

引理2 對于鹽濃度C，我們有如下估計

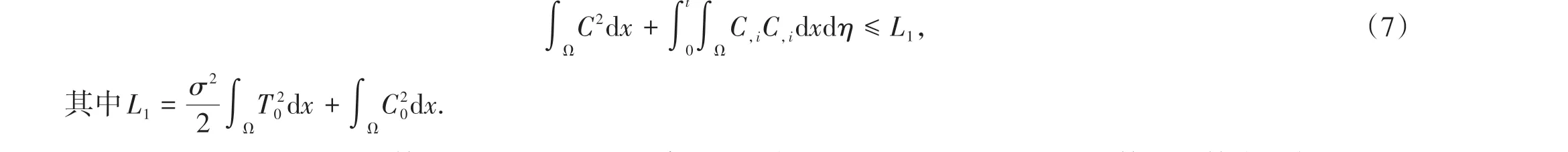
證明在方程組(1)的第4個方程兩邊同時乘以C，并在Ω上積分，由H?lder不等式和算術幾何平均不等式得

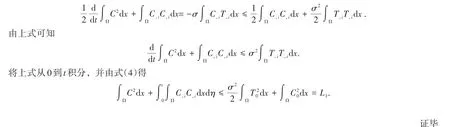
引理3 對于鹽濃度C，我們有如下的4階范數估計

運用式（3），H?lder不等式和算術幾何平均不等式，可得

其中ε1，ε2是大于零的任意常數。

運用方程組(1)的第3個、第4個方程以及H?lder不等式，可得

再運用式（3），H?lder不等式和算術幾何平均不等式，可得

其中ε3，ε4是大于零的任意常數。

聯合式（9）～（10），可得

其中k是大于零的任意常數。

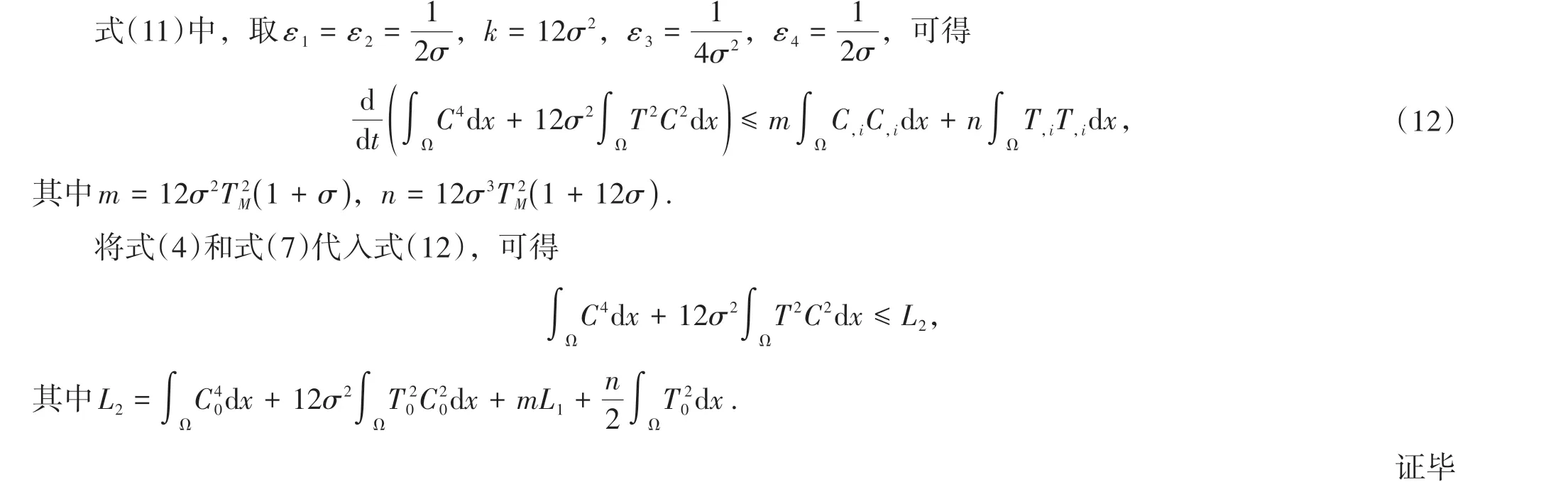
2 連續依賴性

假設(ui，T，C，p)是如下Brinkman方程組初邊值問題的解

邊界條件為

初始條件為

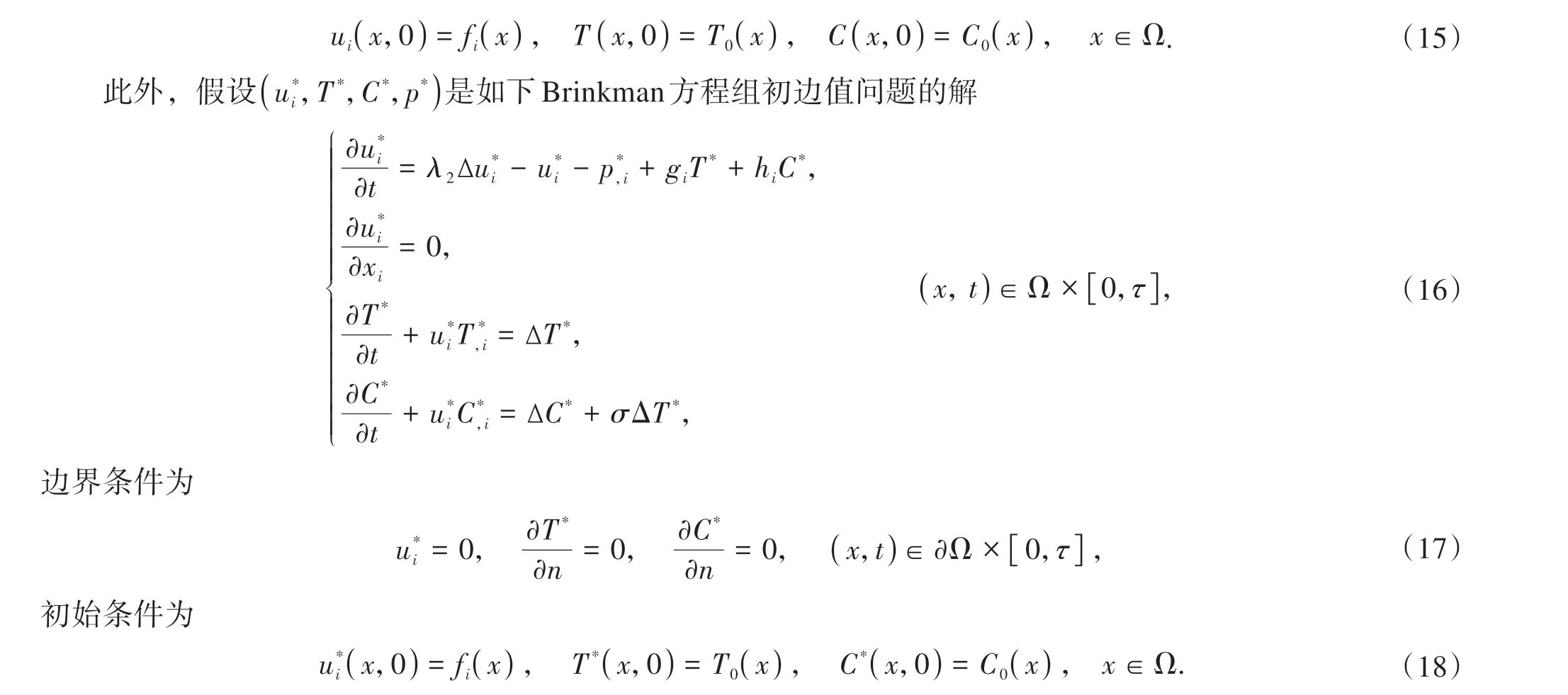
我們定義解的差為：ωi=ui?u*i，θ=T?T*，S=C?C*，π=p?p*，λ=λ1?λ2，則(ωi，θ，S，π)滿足如下初邊值問題

邊界條件為

初始條件為

引理4 對于速度ui，有如下估計

證明 在方程組(13)的第1個方程兩邊同時乘以2ui，并在Ω上積分得

其中k1，k2，k3是大于零的常數。

證明 在方程組(19)的第1個方程兩邊同時乘以2ωi，并在Ω上積分，由式（20）、H?lder不等式和算術幾何平均不等式，可得

對于滿足在邊界上為零的函數E，由文獻（Flavin et al.，1995）的結論，我們有如下Sobolev不等式

其中c1，c2是大于零的常數。

在式（26）中，取E= ωi，可得

聯合式（8）、（25）和（27），可得

注本文我們研究了流體模型的解對Brinkman系數λ的連續依賴性。利用文中的類似方法，依然可以建立方程組的解對其他方程系數的連續依賴性。接下來，將考慮在有界區域內方程組的解對邊界系數的結構穩定性。由于本文中的方程含有?ui項，通過該項較容易得到速度梯度的估計，接著我們將討論不含有該項的情況，此時如何獲取速度梯度的估計將會是面臨的最大障礙，我們會在后續文章中進行研究。