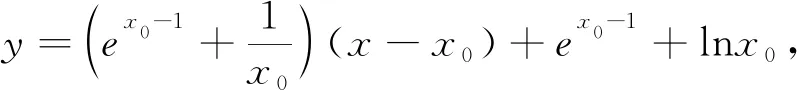對一道調研試題的深入剖析

湖北省武漢市第二中學 (430010) 張 鵠

2022-2023學年度武漢市部分學校高三年級九月調研考試數學第12題為:

若函數f(x)=ex-1+lnx,則過點(a,b)恰能作曲線y=f(x)的兩條切線的充分條件可以是( ).

A.b=2a-1>1B.b=2a-1<1

C.2a-1

試題表述簡潔明了、內涵豐富,重點考查了曲線的切線、函數的零點拐點與極值點、導數放縮等知識和方法,是一道綜合性強、能力要求高的導數壓軸客觀題.顯然,這道調研試題命題與下面的高考題存在一定的關聯.

(2021年新高考Ⅰ卷第7題)若過點(a,b)可以作曲線y=ex的兩條切線,則( ).

A.eb

C.0

可以看出,調考試題體現了新高考Ⅰ卷試題的命題特點與風格,但在考查考生的學科素養和關鍵能力上要求更高,難度更大.

在高三復習教學中如何把握試題之間的內在聯系以及如何發揮試題的潛在功能與價值,是復習備考中需要考慮的重要問題.為此,筆者結合試題剖析本題的思考過程.

首先,根據處理曲線的切線問題的一般解題方法設點設線進行分析.

①若g(x)在(0,+∞)上存在兩個零點,則g(1)=2a-1-b>0,b<2a-1.

②若g(x)在(0,+∞)上只有一個零點,則g(1)=2a-1-b=0,b=2a-1≤-1.

③若g(x)在(0,+∞)上無零點,則g(1)=2a-1-b<0,b>2a-1.

(ii)當0

①當g(1)=2a-1-b=0即b=2a-1時,g(x)有兩個零點,此時-1

②當g(1)=2a-1-b>0且g(a)=f(a)-b<0,即f(a)

③當g(1)=2a-1-b<0或g(a)=f(a)-b>0即b>2a-1或b

(iii)a>1時,令g′(x)=0,則x=a或1.

①當g(1)=2a-1-b=0即b=2a-1時,g(x)有兩個零點,此時b=2a-1>1,選項A正確.當g(a)=f(a)-b=0即b=f(a)時,g(x)也有兩個零點,此時b=f(a)>1.

②當g(1)=2a-1-b<0且g(a)=f(a)-b>0,即2a-1

③當g(1)=2a-1-b>0或g(a)=f(a)-b<0即b>f(a)或b<2a-1時,g(x)有一個零點.

綜上所述,答案為AD.

圖1

(Ⅰ)曲線存在一條切線的情形有:

①當點P(a,b)為拐點G(1,1)時,過點P(a,b)能作曲線y=f(x)的切線只有一條,即直線l;

②當點P(a,b)在直線l上且a≤0時,b=2a-1≤-1,過點P(a,b)能作曲線y=f(x)的切線只有一條,切點橫坐標等于1;

③當點P(a,b)在直線l上方且02a-1,過點P(a,b)能作曲線y=f(x)的切線只有一條,切點橫坐標大于0而小于1;

④當點P(a,b)在曲線y=f(x)下方且0

⑤當點P(a,b)在直線l下方且a>1時,b<2a-1,過點P(a,b)只能作曲線y=f(x)的一條切線,且切點橫坐標大于1;

⑥當點P(a,b)在曲線y=f(x)上方且a>1時,b>f(a)>1,過點P(a,b)只能作曲線y=f(x)的一條切線,且切點橫坐標大于0而小于1.

(Ⅱ)曲線存在兩條切線的情形有:

①當點P(a,b)在直線l下方且a≤0時,b<2a-1≤-1,過點P(a,b)恰能作曲線y=f(x)的兩條切線,例如圖1中的過點P的切線m,n;

②當點P(a,b)在直線l上且0

③當點P(a,b)在曲線y=f(x)上且0

④當點P(a,b)在直線l上且a>1時,b=2a-1>1,過點P(a,b)恰能作曲線y=f(x)的兩條切線,其中一條切線為直線l,另一條切線的相應切點的橫坐標大于1;

⑤當點P(a,b)在曲線y=f(x)上且a>1時,b=f(a)>1,過點P(a,b)恰能作曲線y=f(x)的兩條切線,其中一條為在點P處的切線,另一條切線的相應切點的橫坐標大于0而小于1.

(Ⅲ)曲線存在三條切線的情形有:

①當點P(a,b)在曲線y=f(x)的上凸部分、直線l以及y軸所夾的陰影區域內(不含邊界)(如圖左下方陰影部分)時,f(a)

②當點P(a,b)在曲線y=f(x)的下凸部分的下方與直線l所夾陰影區域內(不含邊界)(如圖右上方陰影部分)時,2a-11,過點P(a,b)恰能作曲線y=f(x)的三條切線.

(Ⅳ)曲線不存在切線的情形有:當點P(a,b)在直線l上方且a≤0時,b>2a-1,過點P(a,b)不能作曲線y=f(x)的切線.

通過從數和形兩方面對這類問題進行深入的剖析,得到本文中的調考試題與高考真題的通解通法:先畫出相應的函數圖像,挖掘圖像背后的各種函數性質,如單調性,凸凹性等,然后再找出特殊點(如拐點)處的切線,考察切線與曲線分割的各個平面區域(含邊界),過這樣的每個區域及其邊界的點向曲線作切線,分析并寫出對曲線的切線條數構成影響的各種因素(如參數之間的數量關系).若要求對上述剖析過程進行邏輯推理,則不難結合前面圖像分析過程并利用相關定理和方法對各種情形進行嚴格論證.