單位分數跨集中阻尼弦本征解的結構及其性質

鄭罡，王夢麗，廖偉，張曉東

［省部共建山區橋梁及隧道工程國家重點實驗室（重慶交通大學），重慶400074］

斜拉索的減振問題迄今仍是工程界重視的實際問題［1-2］，在索端安裝阻尼器對拉索低階模態的減振效果已得到證明，并廣泛用于工程實際中［3-5］.隨著斜拉橋跨度的增大，高階模態的振動問題引起了新的重視［6-11］，因此有必要進一步研究拉索-阻尼（器）系統本征解的結構及性質.

研究中常將拉索-阻尼（器）系統簡化為帶有集中阻尼的張緊弦［12-15］，簡稱集中阻尼弦［16］.就作者掌握的資料，文獻［14-16］均給出了一致的超越函數形式的頻率方程，鑒于求解超越方程的困難，文獻［14］在阻尼（器）充分靠近弦端時，給出了近似條件下本征值的解析表達式；文獻［15］以數值方法求得系統本征解，并繪制阻尼（器）位于有理數位置時的頻率與阻尼（器）位置關系圖；文獻［16］給出了阻尼（器）位于跨中時的解析解.注意到，文獻［14］引入了阻尼（器）位于弦端的假設，并在此假設下進行了近似解析求解；文獻［15］用數值方法避開了超越方程解析求解的困難；文獻［16］則針對單一案例（即集中阻尼位于跨中的情況），得到頻率方程的代數形式.由上述文獻成果可知，集中阻尼弦本征問題的困難仍集中于其超越方程的解析求解.注意到，文獻［16］在特殊情況下首次得到了代數形式的頻率方程，并求得該情況下的解析解，因此本文嘗試利用頻率方程代數化進一步探索解析求解的路徑，以便于利用代數方程相關理論（如代數基本定理）實現該問題解析求解的突破.

同時注意到，文獻［16］采用的方法僅適用于阻尼（器）位于跨中這一情況，對于其他情況［如本文所討論的阻尼（器）位于1/n跨位置，且n≥3］不適用.因此，本文利用雙曲函數多倍角公式突破文獻［16］的頻率方程代數化方法僅適用于單個案例（即集中阻尼位于跨中）的限制，使頻率方程代數化過程適用于集中阻尼置于任意單位分數跨的情況.進一步，對于所得代數方程可解析求解的若干情形（即n=2，3，4，5時），求得集中阻尼弦本征問題封閉形式的解析解，當n=2 時，自然退化為文獻［16］的結果.最后，基于新導出的代數方程和解析解，討論解的結構和性質，從而克服了非解析方法（如文獻［15］的數值方法）在討論解的結構（如解支間的相互關系等）方面存在的固有困難.

1 問題描述

考慮的問題如圖1 所示，其具有線質量密度，張力，弦長，阻尼（器）位于張緊弦上處，并且阻尼（器）位置滿足

圖1 帶有集中阻尼的張緊弦Fig.1 A tension string with a lumped damping

該帶有集中阻尼的張緊弦的自由振動方程可以寫為［17］：

式中：為有量綱本征值. 引入以下無量綱參數和函數：

即可根據文獻［16］的方法對圖1 所示系統進行徹底的歸一：

該歸一化系統具有單位線質量密度m，單位張力T，單位弦長l，并在1/n跨位置設有線黏性阻尼（器），其頻率方程為［16］：

式中：p為無量綱本征值，根據該方程知，其分母shp若為0，則方程無意義，而實際上，當shp為0 時，p為純虛數，此時系統做無衰減自由振動，不受阻尼影響. 這類振動對應于阻尼（器）位置恰好為無阻尼弦自由振動本征函數駐點的情況，為文獻［16］中討論的Ⅱ類本征解，故本文對此類解不展開討論，而重點研究分母shp不為0的情況，對應于阻尼（器）置于非無阻尼弦自由振動本征函數駐點，即Ⅰ類本征解.

由于復頻率方程式（5）為超越方程，其一般通過數值手段求解.但在某些特殊情況下，即阻尼（器）位于單位分數跨時，可將復頻率方程從超越方程形式轉化為代數方程形式，從而利用代數基本定理對方程解的結構及其性質進行詳細討論.

2 復頻率方程代數化

針對阻尼（器）位于弦單位分數跨的情況，將阻尼（器）位置xd=1/n代入復頻率方程式（5）中，并化簡得：

注意到式（6）中雙曲函數自變量存在倍數關系.利用正弦函數倍角公式［18］以及雙曲函數與三角函數的關系推得雙曲正弦函數倍角公式：

根據雙曲余弦函數ch（p/n）的性質知，其值必不為0，故令式（8）除以chn（p/n），則方程未知數僅為th（p/n）：

注意到當th（p/n）為0 時等式始終成立，此時sh（p/n）為0，根據第1 節對其討論可知，該解屬于Ⅱ類本征解，故不再對此進行討論.當其不為0 時，令z=th（p/n）得：

式中：ar為奇數次項系數；bm為偶數次項系數.

至此，復頻率方程式（5）轉化成關于z的n-1 次方程式（11），且此方程不存在零解.需要注意的是，該方程的解是關于阻尼系數的函數.

根據z=th（p/n），本征值p可有如下表達：

式（13）為對數函數，其具有多值特性.求解代數方程式（11），將其根代入式（13），可利用方程根的序列對本征值p的解進行歸類，即所有本征值p可歸為若干解分支，每一解支一一對應于代數方程的每一個根.這種解支關系稱為解的結構.后文將從解的結構角度對集中阻尼弦系統進行研究.

3 解的結構與性質

根據代數基本定理的推論：復數域中，n次代數方程有且僅有n個根.則求解n-1 次代數方程式（11），可得n-1 個根，將其根代入本征值對數表達式（13）后，一個根可求出一組本征值，故頻率方程有且僅有n-1 個解支，并且解支的具體個數與阻尼（器）布設位置有關.

本征值對數表達式（13）亦可寫為復數形式p（i）=σ（i）+jω（i），其中j 為虛數單位，上標i表示第i個解支.由對數函數相關公式得本征值實、虛部表達式：

式中：常數s=0，±1，±2，±3，…；σ是本征值的實部，由于對數衰減率除以振動周期即為本征值實部的相反數，這表明本征值實部的相反數本質上是單位時間對數衰減率，故將本征值實部的相反數命名為單位時間對數衰減率，其符號記為“η”，代表單位時間內自由振動衰減的快慢；ω是本征值的虛部，為系統圓頻率，簡稱頻率.

對于系統的單位時間對數衰減率，由式（14a）可知：

1）當同時給定阻尼（器）位置與阻尼系數時，同一解支下的各階本征值實部均相同，這表明該解支所表征的系統運動具有相同的單位時間對數衰減率，與模態階次無關.

2）單位時間對數衰減率解的個數與解支個數一致，而解支的個數與阻尼（器）位置有關，故系統單位時間對數衰減率的具體個數與阻尼（器）位置有關，為n-1個.

結合上述兩條發現，系統單位時間對數衰減率具有兩條性質：一是單位時間對數衰減率解的個數有限，其具體個數與阻尼（器）位置有關；二是系統存在兩階幅值和能量衰減速度相同的模態.當系統第k1階和第k2階本征值同屬于第i個解支時（k1＞k2），兩者單位時間對數衰減率相等，經過相同時間Δt時，兩階模態的位移響應幅值均按指數項eσΔt衰減，故兩階模態的幅值和能量衰減速度相等.

對于系統的頻率，由式（14b）知：

1）同一解支下鄰階本征值的虛部差值相同，即各階頻率構成等差數列.該性質類似于無阻尼弦鄰階頻率差值為（其中.注意到，由于布設了集中阻尼，任意解支下的各階頻率不再是某個頻率（基頻）的整數倍，但仍保留差值為常數的性質.

2）由于同一解支下鄰階本征值的虛部差值為常數，因此無法充分保證在單一解支內各階本征值具有共軛性.實際上，這點是由代數方程根的性質決定的，即對于代數方程，若出現復根，則必為成對的共軛復根，這就意味著單一根所對應的解支通常無法滿足共軛關系，需將方程另一共軛根對應的解支考慮在內，方可構成共軛關系.關于這點將在下文結合具體算例進行說明.

值得注意的是，結合上述關于單位時間對數衰減率與頻率的討論，對于任一解支下的各階本征值，只需求得每一解支中的某一組單位時間對數衰減率和頻率，即可得解支下完整的解.

上述關于系統單位時間對數衰減率和頻率兩者的討論是從解的結構角度出發的，揭示了集中阻尼弦自由振動的一般通用性質.但注意到，兩者的大小一般隨著阻尼系數c的變化而變化，為進一步研究其性質，下文將利用代數方程式（11），從解析角度探究兩者隨阻尼系數c變化的規律.

可以發現，當n≤ 5時，代數方程式（11）為4次及以下方程，可由求根公式求得本征值閉合解，此有助于詳細討論本征值各解支的性質.表1 提供了n=2、3、4、5（即二分點跨、三分點跨、四分點跨和五分點跨）四個集中阻尼弦系統代數方程的系數，根據表1和代數方程相應的求根公式，即可求出系統本征值閉合解.

表1 代數方程系數表Tab.1 Coefficient of the algebraic equation

將表1 中的系數代入代數方程式（11）中，將求出的根代入本征值表達式（13）中，即可求得本征值的閉合解析解，圖2～圖5 分別為四個系統單位時間對數衰減率和頻率隨阻尼系數變化曲線.

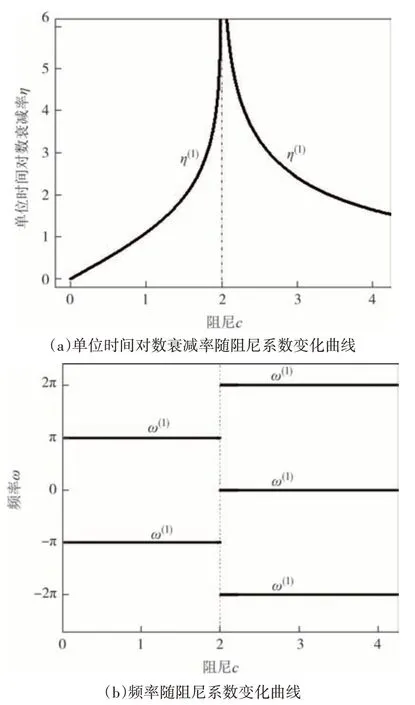
圖2 二分點跨集中阻尼弦Fig.2 The taut string with a lumped damping at midspan

圖3 三分點跨集中阻尼弦Fig.3 The taut string with a lumped damping at one-third-span

圖4 四分點跨集中阻尼弦Fig.4 The taut string with a lumped damping at quarter-span

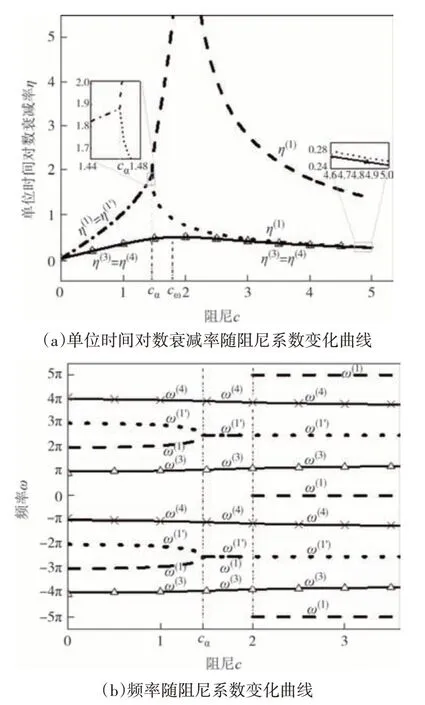
圖5 五分點跨集中阻尼弦Fig.5 The taut string with a lumped damping at one-fifth-span

由圖2（a）、圖3（a）、圖4（a）、圖5（a）可知，上述四個系統均存在一特殊解支（記為p（1）），對于該解支下的單位時間對數衰減率，當阻尼系數從0 增加至2時，其從0 單調增加至無窮大；當阻尼系數從2 增加至無窮大時，其從無窮大單調減小至0.可以發現，當阻尼系數c取2 時，解支p（1）所表征的各階運動將會瞬時衰減至0，阻尼振動將被瞬間抑制.

由圖2（b）、圖3（b）、圖4（b）、圖5（b）和頻率表達式（14b）可知，對于特殊解支p（1）的頻率，當c大于2時，其頻率為常數snπ，當s=0 時，頻率為0（系統做非震蕩衰減運動）.當阻尼系數c小于2 時，根據阻尼（器）位置的不同，頻率出現不同現象：當n為偶數時，其為非零常數（s+1/2）nπ；n為奇數時，其在阻尼系數小于某一值（該值用cα表示，且cα＜ 2）時隨阻尼變化，當阻尼系數在cα和2 之間時，其為非零常數（s+1/2）nπ，與n為偶數時一致.注意到，對于特殊解支p（1）出現常數的情況，其單位時間對數衰減率不為0，這點與阻尼（器）位于無阻尼弦駐點（頻率同樣為常數）的情況不同.

可以發現，當阻尼（器）位于奇數點時，除特殊解支p（1）的單位時間對數衰減率在阻尼系數c取2 時存在無窮大不可導點外，還出現了一新解支的單位時間對數衰減率，在阻尼系數c取cα時同樣不可導（記為p（1'），以此代替p（2））.解支p（1'）的單位時間對數衰減率，在阻尼系數c從0增加至cα時，從0單調增加至最大值；在阻尼系數c從cα增加至無窮大時，其從最大值單調減小至0.其頻率在阻尼系數小于cα時隨阻尼系數變化，在阻尼系數大于cα時為非零常數n（s+1/2）π.

值得注意的是，在此阻尼（器）位置條件下，解支p（1）和解支p（1'）在阻尼系數c小于cα時互為共軛解支，即此時兩者單位時間對數衰減率相同，頻率互為相反數；當阻尼系數c在cα和2 之間時，兩者不再共軛，前者單位時間對數衰減率隨阻尼系數的增大而增大，后者單位時間對數衰減率隨阻尼系數的增大而減小，但兩者頻率為相等的常數；當阻尼系數超過2時，兩解支的頻率仍為常數，但值不相同.

當n大于3 時，出現了一類新的解支，其單位時間對數衰減率隨阻尼系數的變化而變化，在阻尼系數c取cω（cω≠cα）時，取得最大值；其頻率亦隨阻尼系數連續變化.同時注意到，該類型的解支均兩兩以共軛對形式出現，且對于任意阻尼系數都成立.

結合上述關于解支的討論，根據其隨阻尼系數變化的特點，可將其歸納為3 類：第一類解支的頻率均依賴于阻尼（例如四分點跨系統的解支p（2）和p（3），五分點跨系統的解支p（3）和p（4））；第二類解支的頻率均不受阻尼影響（例如二分點跨情況下的解支p（1），四分點跨情況下的解支p（1））；第三類解支綜合第一類和第二類解支特點，頻率在一定范圍內（0＜c＜cα）與阻尼系數取值有關，一定范圍內（cα＜c）為常數（例如三分點跨情況下的解支p（1）和p（1'），五分點跨情況下的解支p（1）和p（1'））.

實際上，三類解支與復頻率代數方程式（11）的根的情況一一對應：第一類解支對應于方程的共軛復根，故該類解支以共軛解支對形式出現，解支個數必為偶數，且此類解支僅當n≥ 4 后才會出現；第二類解支對應于方程的實根，對于任意阻尼系數，該實根均為負實根，此類解支僅當n為偶數時才會出現；第三類解支亦對應于方程的實根，但與第二類解支不同的是，該根的情況隨阻尼系數而變化，其在一定阻尼系數范圍內（0＜c＜cα）為復數根，而在另一阻尼系數范圍（cα＜c）內為實數根，故該類解支亦兩兩成對出現，并在一定阻尼系數范圍內，互為共軛解支，此類解支僅當n為奇數時才會出現.

將這三類解支的頻率與阻尼（器）位置的關系與文獻［15］進行對照發現（圖6），第一類解支對應于區域1和區域3，當阻尼系數從0增加至無窮大時，其阻尼比從0 增加至最大值后再減小至接近0；第二類解支對應于1 類和2 類垂直解，當阻尼系數從0 增加至無窮大時，其阻尼比從0 增加至1；第三類解支對應于中間特例，即區域1 與區域2、區域3 與區域2 的交界線，由于此類解支均兩兩成共軛對形式出現，故其阻尼比需兩兩一對進行討論，在阻尼系數從0 增加至無窮大時，兩相鄰階阻尼比從0 開始增加，在中間某一點相交后，其中一階阻尼比減小至接近0，另一階阻尼比增加至1，綜合了第一類和第二類解支阻尼比的特點.

圖6 三類解支的ω-xd關系與文獻［15］的對比圖Fig.6 Comparison of the ω-xd relation of the three types solution branches with reference ［15］

4 結論

本文在阻尼（器）位于單位分數跨的條件下，推導出關于頻率方程的代數方程形式，根據代數方程的相關性質，從解的結構角度對集中阻尼弦系統進行討論，結果表明：

1）系統所有本征解可歸為n-1 個解支，且解支的具體個數與阻尼（器）位置有關.

2）對于同一解支，各階本征值實部（其相反數即單位時間對數衰減率）均相同，各階本征值虛部（即頻率）構成等差數列.

根據具體算例，從解析角度進一步探討了本征值隨阻尼系數變化的規律，并將所有解支歸結于三類進行討論，結果表明：

1）第一類解支的頻率均依賴于阻尼.該類解支對應于代數方程的共軛復根，均以共軛形式出現，僅當n≥4時才會出現，且解支個數為偶數.

2）第二類解支的頻率均不受阻尼影響.該解支對應于代數方程的負實根，僅當n為偶數時才會出現，其有且只有1個.

3）第三類解支綜合第一類和第二類解支特點，頻率在一定范圍內（0 ＜c＜cα）與阻尼系數取值有關，一定范圍內（cα＜c）為常數.該類解支對應代數方程的根在0 ＜c＜cα時為共軛復根，cα＜c時為實根，且僅當n≥4時才會出現.