基于神經網絡PID 的多支路流量遠程控制仿真*

李澤東 孟祥印 彭 杰 周亮君

（西南交通大學機械工程學院 成都 610031）

1 引言

多支路流量控制經常運用在我們的日常生活和工業生產各個角落，如天然氣輸配、多支路調壓站等。眾所周知，氣體輸送系統是由多個支路同時配送，并且系統是一個相互聯系的整體，各個支路之間會相互影響，既某個支路的流量變化，勢必引起其它支路流量變化，支路與支路之間存在耦合關系［1］。如何控制支路變化，讓支路流量按照預定的輸送變得格外重。相反，如果無法準確控制各支路流量的變化，可能產生不堪設想的后果。例如，如果某個支路的流量過大，可能會造成超出其支路設備的最大限值而導致損壞，使整個系統不能正常運行，既所謂的失調［2～3］。如果系統失調長期存在，導致流體輸送系統的部分支路設備高負荷運行，而另一支路設備卻較低負荷工作，使得系統的整體使用壽命縮短。

針對系統中存在的這種流量失調現象，以及使得各支路能夠按照設定的流量進行控制，應當采用相應的措施，對管網進行平衡調節，盡量減少失調的程度，保證多支路氣體輸配系統的長期可靠安全運行［4～6］。并且隨著網絡技術的發展，遠程調流成為氣體輸送控制和輸配調度的重要技術手段，迫切需要提高系統參數調節的自動化、網絡化和智能化。在流量相互作用的多支路氣體輸配系統中，研究如何遠程控制壓力、調節和平衡支路間流量，并能自辨識、自適應不同參數的系統，具有一定的理論意義和重要的市場應用價值。

2 多支路流量調節模型

2.1 系統總體設計方案

在多支路系統中，由于各支路之間存在耦合關系，某個支路流量變化必然影響其他路流量變化，并且這些變化都是非線性的，因此，如果僅僅通過分別單獨對每個支路調節不但費時費力，并且很難精準控制各支路流量。本文通過神經網絡PID 同時控制多條支路，使流量得到精確控制。本文以三條支路為例，系統整體布局如圖1。

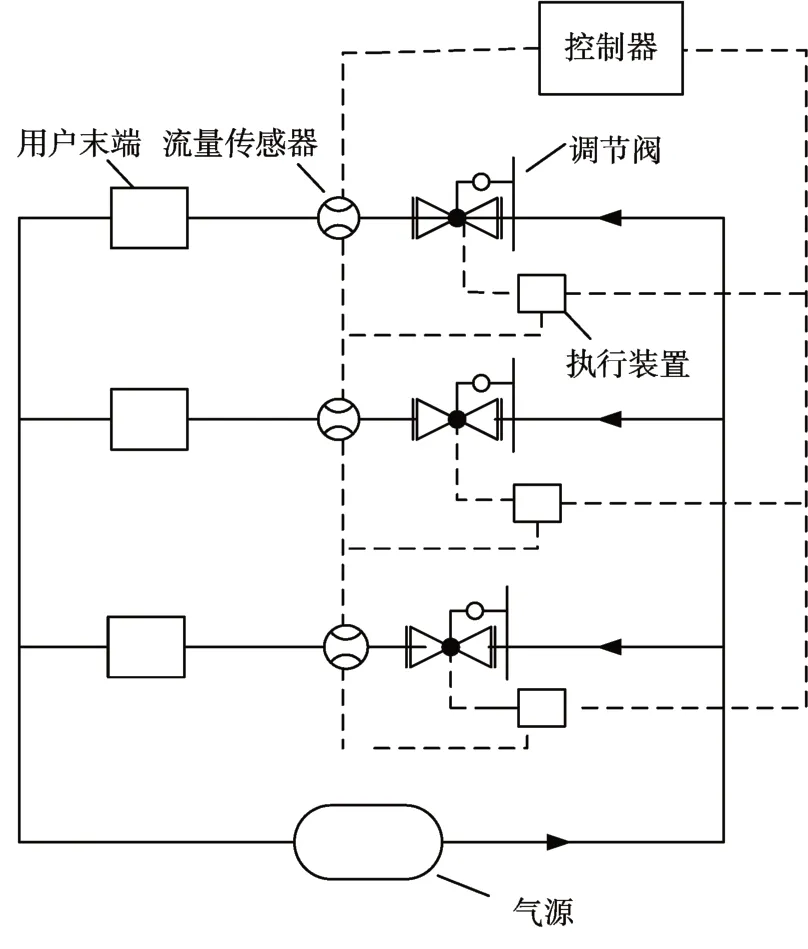
圖1 多支路流量控制整體布局圖

如圖1 所示，在整個多支路流量控制系統中，每條支路有相應的調節閥、流量傳感器、控制器、執行裝置等。流量傳感器實時監測各支路流量，控制器根據控制信號控制執行裝置，進而控制閥門的開度，最終實現流量的控制。

系統主要由遠程控制中心和調節閥終端組成，調節閥終端主要有微處理器、步進電機控制模塊、流量采集模塊、數據通信模塊。遠程控制中心主要包括數據通信模塊，服務平臺、用戶端等［7］。調壓閥終端通過Internet將流量數據傳送給遠程控制中心，遠程控制中心發送信號來控制閥門開度進而控制流量大小［8］。

2.2 調節閥閥門開度控制

調節閥控制系統主要由控制器、步進電機、蝸輪蝸桿傳動機構、調節閥構成［9］。具體控制過程為控制器根據設置流量和流量傳感器檢測實際流量對比，根據調壓算法進行運算，形成相應的控制信號，控制步進電機轉動，蝸輪蝸桿將步進電機的轉動變成絲杠的直線運動，進而控制調節閥門的開度，最后將控制所得流量反饋比較，形成閉環控制。控制原理，如圖3。

圖3 電動燃氣調節閥系統控制原理

2.3 調節閥系統數學模型建立

為了更好地分析調節閥的控制系統的響應，需要對調節閥控制系統進行數學建模，通過參考文獻［10］對步進電機、傳動系統（電機軸，減速器，絲杠軸，傳感器）、調節閥建模。得到了被控系統傳遞函數近似如下：

主要參數如表1所示［10］。

表1 調節閥系統模型參數［10］

3 多輸入多輸出神經網絡PID解耦

在大多數多輸入多輸出（MIMO）的系統中，都存在耦合現象，然而，在工業控制中希望各個支路之間耦合盡量削弱甚至消除，才能使系統安全平穩的運行。傳統的解耦控制器可以在一定程度上實現解耦，但解耦控制器的設計繁雜，計算量大。因此，本文以神經網絡為基礎，實現對多輸入多輸出系統的解耦控制［11～12］。

3.1 單輸出神經網絡PID

本文多輸入多輸出系統以三條支路并聯構成，是一個6 輸入3 輸出的多變量耦合系統，控制器是由3 個單輸出PID 神經網絡（SPIDNN）構成的多輸出PID 神經網絡（MPIDNN），單輸出PID 神經網絡（SPIDNN）輸入是由兩個神經元構成，對應系統分別是某支路的設定流量和流量傳感器檢測的實際流量，隱含層分別由比例（P）、積分（I）、微分（D）3個神經元構成，輸出層只有一個神經元，輸出控制信號［13］，控制電機的轉動。結構如圖4。

圖4 SPIDNN機構圖

3.2 多輸出神經網絡PID解耦

多輸出PID 神經網絡解耦控制器是有多個SPIDNN并聯而成，輸入層到隱含層獨立運算，但隱含層到輸出層互相交叉關聯，通過對隱含層的神經元定義不同的激活函數，使得比例、積分、微分之間有相應的關系［14］。根據誤差函數，通過正向計算和反向計算，不斷地訓練學習，修改完善連接權值，使得流量得到控制［15］，結構如圖5。

圖5 MPIDNN機構圖

3.3 PID神經網絡多變量解耦控制算法

輸入層：

輸入層包含有6 個神經元，輸出神經元的數據等于輸入的神經元數據，關系如下：

式中：m為并聯網絡序號；γm(k) 為設定流量值；ym（k）為流量監測值；μmi為輸入層神經元輸出值。

隱藏層：

隱藏層有9個神經元，比例、積分、微分各3個，各個神經元的輸入值可以表示為

比例神經元：

積分神經元：

微分神經元：

式中，j 為子網絡中隱含層神經元序號；χmi(k)為各子網絡輸出層神經元輸出值；ωij為各子網絡輸出層到隱藏層的連接權重。

輸出層：

輸出層有三個神經元，分別控制三個調壓閥的電機轉動，計算公式如下：

式中，h表示輸出層神經元序號，μmj(k)為隱藏層各神經元輸出值，ωjk為隱藏層到輸出層的連接權值。

連接權值修正：

神經網絡PID 通過控制誤差來反向運算調整連接權重，使誤差函數逐步減小，誤差函數為

權重修正：

輸出到隱藏層：

隱藏層到輸出層：

η為學習率。

4 多支路流量調節模擬仿真

通過將表1 的數值帶入式（1），采樣時間設置為0.01s時候，經過z變換得到的傳遞函數為

由z 變換可以求得系統的差分方程表達式如下：

設三條支路的傳遞函數差分方程分別為Y1(k)、Y2(k)、Y3(k)，為了簡化方程，將上述方程用以下參數代替：

由于三條支路之間存在耦合，并且耦合作用與管路系統、調節系統有關。因此，本文采用以下近似耦合關系進行仿真：

根據神經網絡學習速率選取規則，取η=0.06。初始權值為隨機數，三個被控量的目標值設置為0.7、0.65、0.6，循環次數設置為200，仿真圖像如圖6～7所示。

圖6 多支路流量控制控制階躍響應圖

圖7 多支路流量控制誤差圖

從圖6～7 可知，三條支路在大約0.2s 后趨于穩定，并且各個支路實際輸出和控制目標有之間有一定的誤差，系統整體誤差在0.0061左右。

針對以上存在的反應速度慢，神經網絡容易陷入局部最優造成的實際輸出與控制目標誤差較大的問題。在以上基礎上加入動量項以及神經元系數如下。

增加動量項：

增加神經元系數：

其中η1=0.001，kp=1.5、ki=1、kd=10、其他參數不變，所得的仿真圖如圖8～9所示。

圖8 改進后多支路流量控制控制階躍相應圖

圖9 改進后多支路流量控制控制誤差圖

從仿真圖可以看出，三個控制量在0.06s 左右全部趨于穩定，整體誤差控制在0.0005，相對于改進前，在速度、誤差、穩定性方面都有大幅度提升。并且實驗表明，PID 神經網絡能夠解決各支路的耦合關系，并且快速地調節各支路流量。

5 結語

本文通過建立系統傳遞函數，使用改進后的神經網絡PID 完成了對具有耦合作用的多支路流量控制，實現了快速、準確地控制各支路流量大小，為多支路流量輸送控制提供了一定的參考。