KR攪拌結合底噴粉新型脫硫工藝的數值模擬

商少偉,賈舒淵,王 強,劉艷賀,王睿之,賀 鑄

(1. 武漢科技大學省部共建耐火材料與冶金國家重點實驗室,湖北 武漢,430081;2. 武漢科技大學鋼鐵冶金及資源利用省部共建教育部重點實驗室,湖北 武漢,430081;3. 中國特種設備檢測研究院,北京,100029;4.中國寶武(寶鋼股份)中央研究院,上海,201900)

KR法鐵水脫硫因具有良好的脫硫動力學條件、較高的脫硫效率及較低成本,是目前應用最為廣泛的鐵水脫硫技術之一[1-3]。該工序中,鐵水流動對脫硫效率有顯著影響,根據其特征可分為三個區域:中心強制渦流區、自由渦流區及弱流區[4]。僅在自由渦流區,鐵水的循環流動可使脫硫劑與鐵水之間發生相對運動,能達到充分混合的效果[5];而在中心強制渦流區,由于表面張力和浮力的作用,脫硫劑難以卷入鐵水內部,并且在攪拌所產生的負壓作用下,大量脫硫劑在該區域凝并[6],即使這部分脫硫劑隨后卷入自由渦流區,也僅在其表層發生脫硫,脫硫劑分散效果不理想,導致脫硫劑因利用程度低而消耗量增大。

為解決脫硫劑先凝并后反應所導致的脫硫劑消耗量增大的問題,相關從業者針對KR方法中攪拌工藝開展了大量的數值模擬和水模型實驗研究[7-10]。例如龍鵬[1]研究發現,在同等潛入深度下,相較于四葉槳,三葉槳能夠使脫硫劑顆粒分布的更加均勻,且下沉深度更大。張送來等[11]認為,攪拌器浸入深度為187.5 mm時,軸向上鐵水平均速度差最大為0.132 m/s,而大速度差有利于脫硫劑的卷入。這些研究通過改善鐵水包內流場促進了脫硫劑脫硫效率的提升,但仍未能很好地解決脫硫劑隨攪拌渦團浸入鐵水過程中的團聚問題[12]。

為此,本文利用Fluent軟件建立鐵水包內各相流的數學物理模型,模擬槳葉旋轉過程,通過在鐵水包底部噴粉的方式,使脫硫劑粉末進入底部弱流區,直接與鐵水發生反應,并在浮力和槳葉的攪拌作用下使之均勻分布在鐵水包內,分析了槳葉攪拌耦合底噴粉時鐵水流動及脫硫劑彌散分布行為,并基于所建模型,對比研究了噴嘴位置對脫硫劑在鐵水包中分布情況的影響。

1 數學模型

1.1 基本假設

本文所建立的數學模型包含以下假設:①氣液兩相均為黏性不可壓縮牛頓流體;②不考慮鐵水包頂渣對流場的影響;③不考慮鐵水溫差引起的熱對流;④假設CaO顆粒為球體,密度不發生改變;⑤假設CaO顆粒與氬氣初始速度一致。

1.2 控制方程

1.2.1 氣液兩相流動及混合過程

本文利用VOF多相流模型模擬氬氣運動過程以及氣液交界面的波動情況,連續方程為:

(1)

式中:α為混合相體積分數,ρ為混合相密度,v為混合相的速度矢量。

動量方程為:

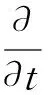
(2)

式中:p為壓力,Fσ為氣液間表面張力,Fother為單位質量離散相傳遞的相互作用動量,μ為混合相黏度,g為重力加速度。

(3)

式中:σ為表面張力系數,設為1.7 N/m;K為自由曲面的平均曲率。

混合相的物理性質與各項的體積分數有關,可表示為:

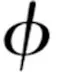
(4)

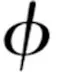
采用κ-ε方程描述氣液兩相流動的湍流特性,其中湍動能κ方程為:

(5)

湍動能耗散率ε方程為:

(6)

式中:Gκ為平均速度梯度產生的湍動能,Gb為浮力產生的湍動能,YM表示可壓縮湍流中波動膨脹對整體耗散率的貢獻,C1、C2、C1ε和C2ε均為常數,σκ和σε分別是湍動能和耗散率的湍流普朗特數,Sκ和Sε分別為湍動能和耗散率的源項,μl為運動黏性系數,μt為湍流黏度。

1.2.2 DPM離散相模型

本文利用DPM離散相模型模擬脫硫劑,其運動遵循牛頓第二定律:

(7)

式中:md和vb分別為離散相的質量和速度;FD、FG、FB、FP、FVM、FL分別是曳力、重力、浮力、壓力梯度力、虛擬質量力和升力,其控制方程為:

(8)

(9)

(10)

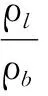
(11)

(12)

式中:Re為相對雷諾數,db為脫硫劑粒徑;CD、CVM、CL分別為曳力系數﹑虛擬質量力系數、升力系數。其中脫硫劑顆粒發生凝并的條件為:

(13)

f的定義式為:

(14)

We的定義式為:

(15)

式中:r1和r2表示脫硫劑粒徑,l為特征長度,f1為脫硫劑與鐵水的表面摩擦系數。

(16)

其中Y表示從0～1的隨機數。當兩個脫硫劑顆粒相撞時,若bcrit>b,則發生凝并。

1.2.3 脫硫模型

在KR法預處理鐵水時,脫硫劑與鐵水中硫元素發生反應,反應式如下:

(CaO) + [S] = (CaS) + [O]

(17)

此外,硫在鐵水中的對流和擴散也影響了脫硫率。本研究綜合考慮上述現象,建立脫硫傳質控制方程[14-16]:

(18)

式中:c為鐵水中硫的濃度;SdeS表示單個脫硫劑顆粒的反應速率;DS表示S元素的擴散系數,即

DS=

(19)

式中:T0為鐵水的初始溫度,R為理想氣體常數。基于Oeters等[17]提出的簡化表面積方法,單個脫硫劑的反應速率SdeS可寫作:

(20)

式中:δ為CaS層厚度,β[S]表示硫從熱金屬到粒子邊界的運動速率。

脫硫反應中,Sh表示硫傳質率和擴散傳質率之比,該參數反映了脫硫劑尺寸、速度和局部硫濃度對脫硫效果的影響:

(21)

式中:dp為脫硫劑的當量直徑,Re和Sc分別為局部雷諾數和施密特數。在脫硫反應中,脫硫劑表面會生成CaS,S元素需要滲透CaS層才能與內部的CaO發生反應,該固相擴散過程降低了脫硫反應速率。

脫硫劑表面的CaS厚度增長速率可表示為:

(22)

式中:MCaS和MS分別為CaS、S的相對摩爾質量,ρ(CaS)為CaS的密度。

1.3 模型的建立

模型中使用的各項物理參數如表1所示。采用滑移網格(SM)模擬攪拌過程,圖1為網格劃分示意圖。將計算域劃分為旋轉區和靜止區,中間為旋轉區,由于其結構復雜,故采用非結構化網格,并對該區網格進行加密處理以提高計算精度,而靜止區采用結構化網格,二者通過交界面進行數據交換。對比分別采用10萬、30萬、60萬、90萬網格的模擬計算結果后可知,60萬與90萬網格的模擬結果差距小于4.7%,故本文選擇采用60萬網格劃分進行模擬計算。另外,本文使用的數學模型已在課題組前期研究中進行了詳細的實驗驗證。并且數值模擬結果與實驗結果符合較好,所建模型的有效性已得到驗證[17-19]。

圖1 模型網格劃分

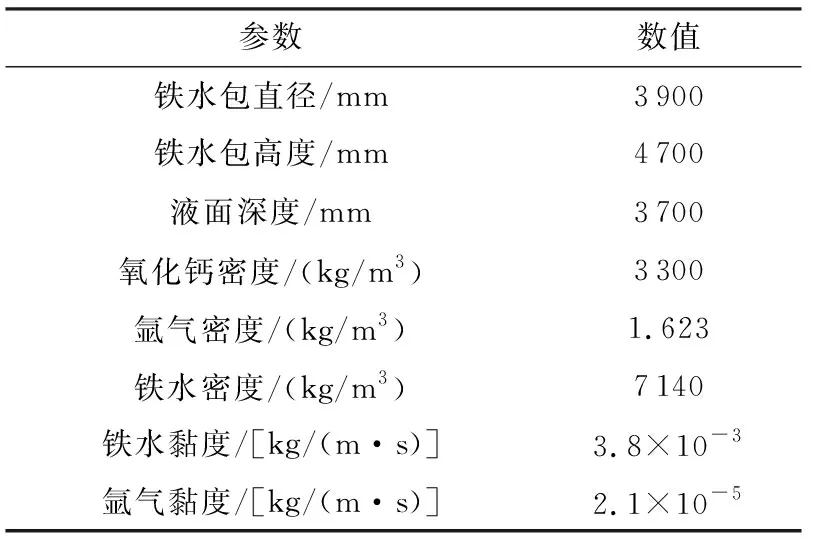
表1 物理參數

1.4 邊界條件及求解方法

鐵水包壁面和底面設為靜止壁面,攪拌槳葉和攪拌軸均為旋轉壁面,轉速為80 r/min,氬氣吹入邊界條件為速度入口,雙孔噴吹速度均為6.9 m/s,噴吹氣量為6000 NL/min,上表面為壓力出口;鐵水初始硫濃度為0.03%,初始溫度為1573 ℃,鐵水包底部和壁面散熱系數均為2000 W/(m2·K)。設定脫硫劑初始速度與噴氣速度一致,初始溫度為300 K。軸對稱噴嘴(藍色短線)的位置如圖2所示,分別距離鐵水包軸心0.4R、0.6R、0.8R。

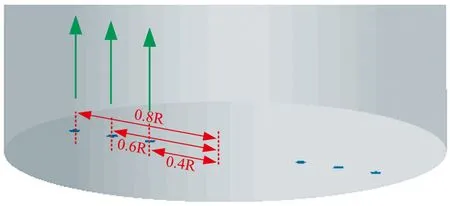
圖2 噴嘴位置分布

使用SIMPLE算法對速度和壓力進行耦合,采用二階迎風格式進行求解,時間步長為0.005 s,計算40 s待流場穩定后,從包底噴入粒徑為0.5～3 mm且呈正態分布的氧化鈣粉末分布情況。

2 結果與分析

2.1 噴吹位置對鐵水包流場的影響

圖3所示為不同位置噴粉時鐵水包內氣體分布情況,可以看出,當噴嘴位置靠近包底中心時(距包底中心0.4R),由于噴嘴間距較近,氣體受鐵水曳力作用,卷吸在一起形成氣柱,氣體更為集中地上浮;隨著噴嘴向壁面靠近,槳葉底部的氣柱直徑逐漸增大,隨著噴嘴間距繼續增大至超過一定值后,槳葉底部氣體難以形成氣柱。氣體上浮至槳葉位置時被高速旋轉的槳葉甩出,隨后上浮至液面,鐵水包上部氣體分布較為均勻。

(a)0.4R (b)0.6R (c)0.8R

圖4為不同位置噴粉下鐵水流場剖面的流線圖與速度云圖,可以看出,在槳葉攪拌作用下,鐵水在近鐵水包壁面處形成上下兩部分。由于氣體上浮能推動鐵水流動,故當噴嘴位置靠近包底中心(距包底中心0.4R)時,槳葉底部鐵水的流速更快,加強了包內鐵水循環流動,促進了鐵水硫濃度的平衡以及加強了鐵水與脫硫劑之間的相對運動,從而提高脫硫效率[7]。當噴嘴位置更靠近壁面(距包底中心0.8R處),如圖4(c)所示,氣體沿著紅色箭頭噴入鐵水包,并沿著該方向逐漸上浮,然而循環流動的鐵水沿著包壁向下流動,氣體上浮使得向下流動的鐵水動能減小,故難以形成較大的自由渦流區,而是在鐵水包底部兩側形成了較小的旋渦,鐵水循環流動性較差。

(a)0.4R (b)0.6R (c)0.8R

2.2 噴吹位置對脫硫劑運動的影響

圖5為不同位置噴粉下脫硫劑從包底噴入鐵水包后的運動軌跡。對脫硫劑從包底上浮至槳葉底部的時間進行統計,得到距包底中心0.4R、0.6R、0.8R時,脫硫劑上浮時間分別為6、8、12 s。當噴嘴位置越靠近壁面,氣體上浮對鐵水運動的推動作用越小,鐵水向上流動的速度越慢,脫硫劑在鐵水包底停留的時間也就越長,這有利于延長包底弱流區的脫硫時間,從而提高脫硫效率。

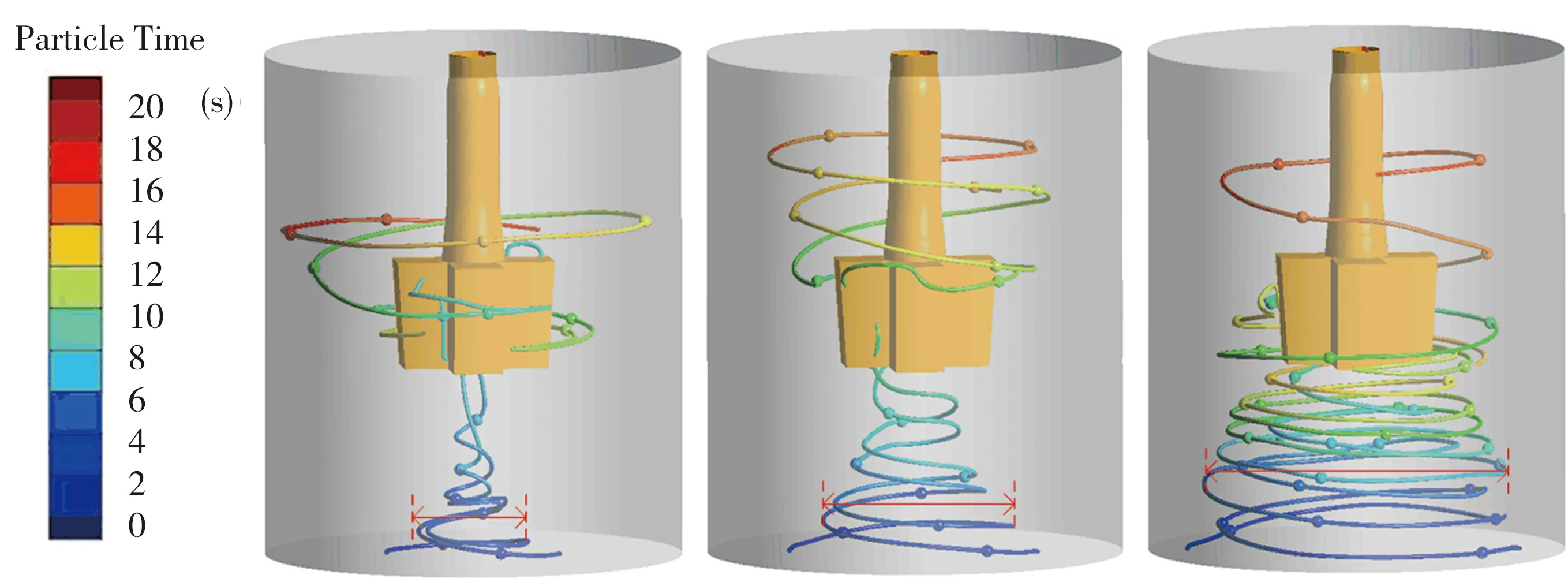
(a)0.4R (b)0.6R (c)0.8R

對槳葉底部以下的脫硫劑運動范圍進行統計,得到噴嘴距包底中心為0.4R、0.6R、0.8R時,脫硫劑運動半徑依次為0.3R、0.5R、0.9R。在槳葉攪拌作用下,包底鐵水從兩側向中心流動,脫硫劑在鐵水作用下向中心運動,故脫硫劑噴入鐵水包的位置越靠近壁面,脫硫劑向中心運動的距離越長。圖6為從距包底中心0.8R位置噴入的脫硫劑不同時刻在鐵水包內的分布情況,可以看出,脫硫劑運動受旋渦影響,在水平方向上的擺動較為明顯,而這種擺動使得脫硫劑在鐵水包底部弱流區的運動范圍增大。

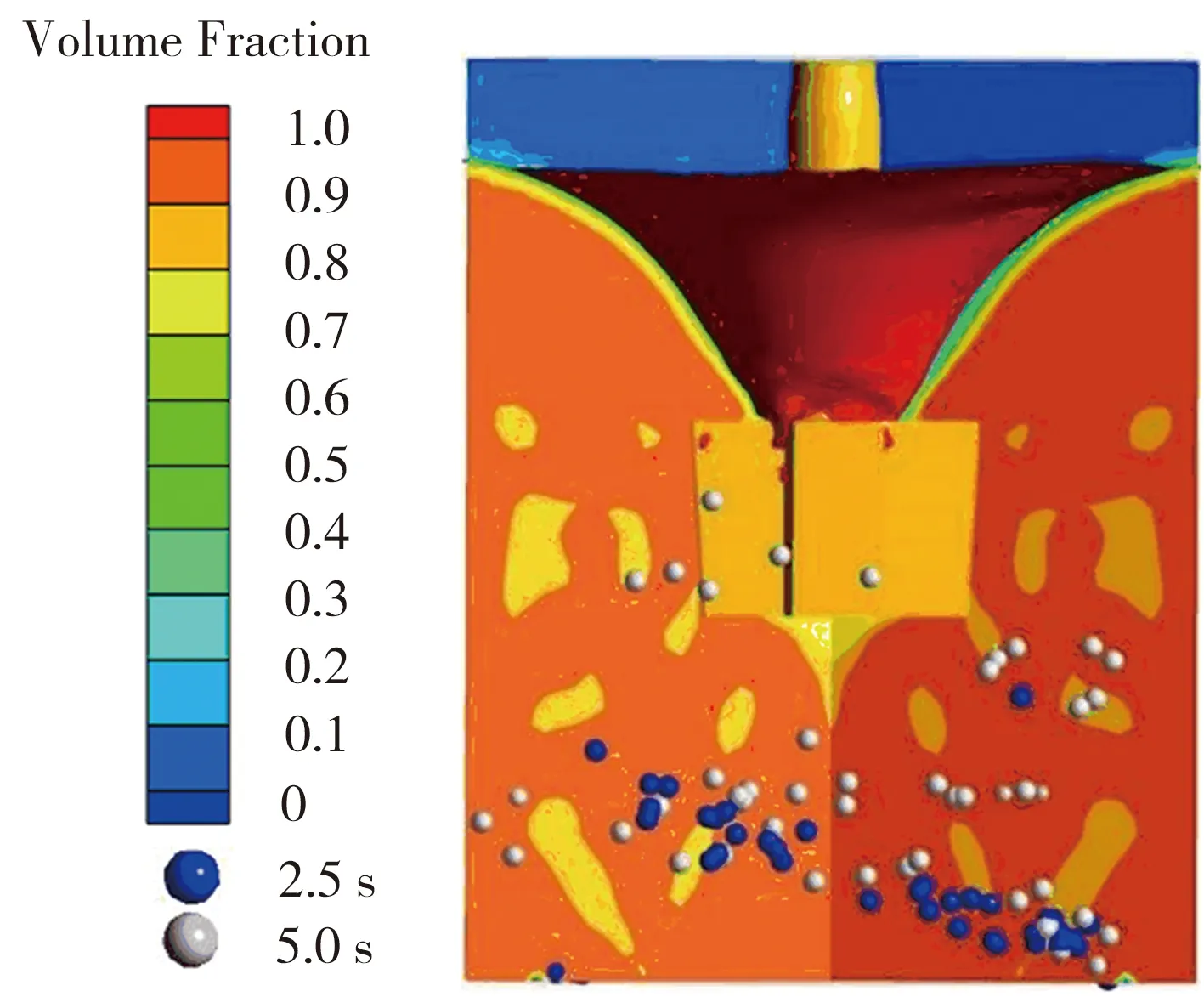
圖6 不同時刻鐵水包內顆粒分布情況(距包底中心0.8R)

2.3 噴吹位置對脫硫劑凝并的影響

圖7為底吹60 s時脫硫劑在鐵水包內分布云圖,可以看出,當噴粉位置距包底中心0.4R和0.6R時,脫硫劑在鐵水包上部聚集,凝并成大粒徑顆粒,而當噴粉位置靠近壁面(距中心0.8R),脫硫劑在鐵水包內分布均勻,凝并程度較低。以槳葉底面為界將鐵水包分為上下兩部分,并對脫硫劑粒徑統計,結果如圖8所示。由圖8(a)可見,從距包底中心0.4R噴粉時,在鐵水包下部有大粒徑的脫硫劑(粒徑≥7.7 mm),這是因為此條件下脫硫劑在鐵水包下部碰撞概率大,故凝并程度更高。由圖8(b)可知,從距包底中心0.4R和0.6R處噴粉時,鐵水包上部存在大粒徑的脫硫劑(粒徑≥9.5 mm),其凝并程度較高,而從距中心0.8R處噴粉,脫硫劑粒徑大部分分布在0.5～6.1 mm之間,凝并程度相對較低。由此可見,從靠近壁面處噴粉能使脫硫劑在鐵水包內分布更加均勻,可有效緩解脫硫劑凝并現象。

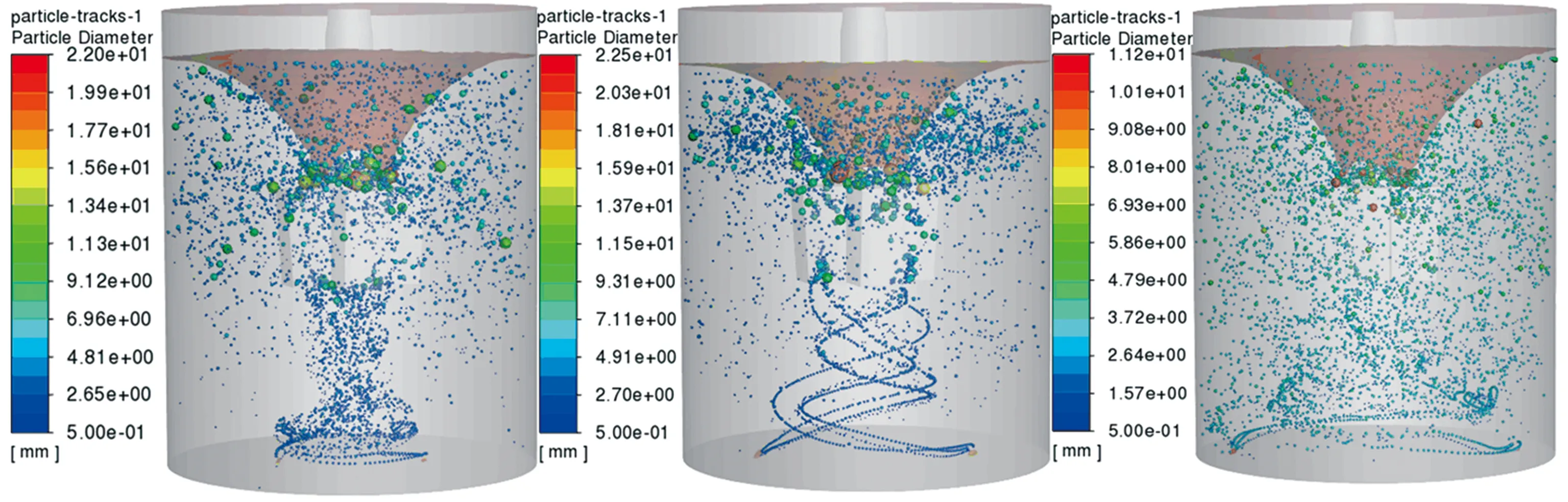
(a)0.4R (b)0.6R (c)0.8R

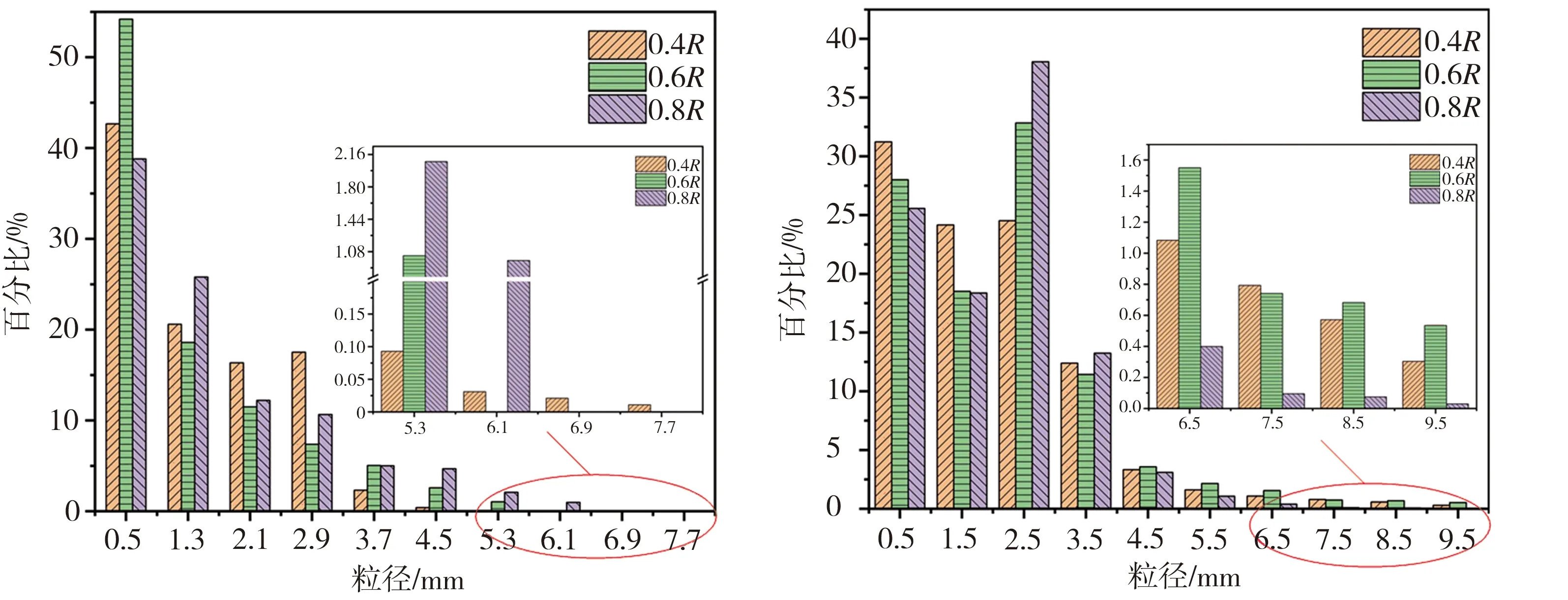
(a)鐵水包下部 (b)鐵水包上部

2.4 底吹加料與傳統表面連續加料的脫硫效率對比

由式(19)～式(20)可知,脫硫劑反應速率與硫的擴散速率及溫度有關,圖9為噴嘴距包底中心0.8R時鐵水包內鐵水溫度分布,由于大量氬氣從容器底部吹入與高溫鐵水進行熱交換,使得容器底部的鐵水發生溫降,但其溫降較小,故對脫硫反應的影響不大。

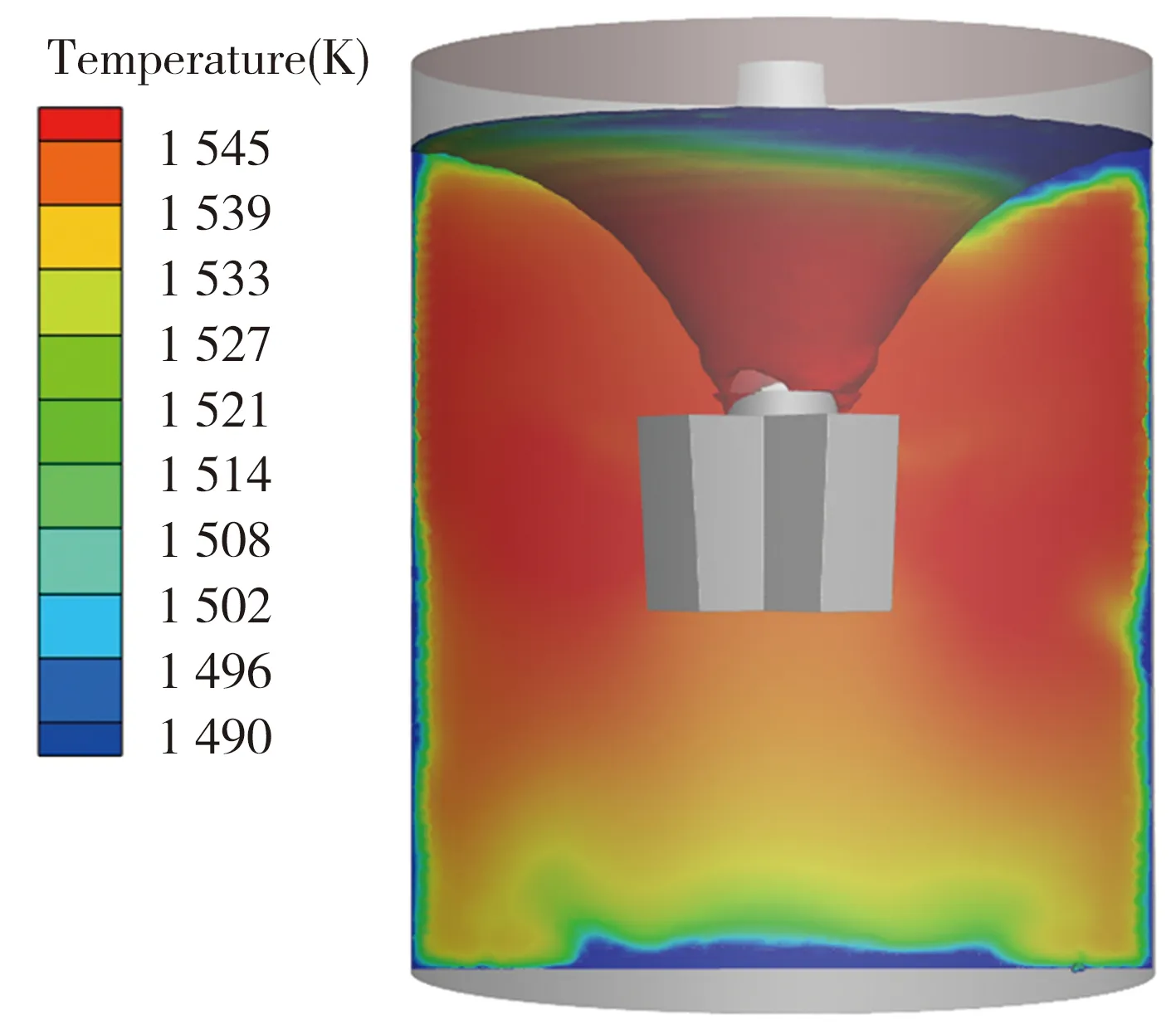
圖9 鐵水包內溫度分布

對鐵水的平均硫濃度進行監測,圖10所示為距包底中心0.8R噴粉時,不同時刻鐵水的硫濃度分布變化。由圖10可見,當脫硫劑進入鐵水包后在底部與鐵水發生脫硫反應,在渦流影響下,硫濃度較高的鐵水從兩側向容器底部流動,不斷與新噴入的脫硫劑發生反應,這進一步提高了脫硫劑的脫硫效率。

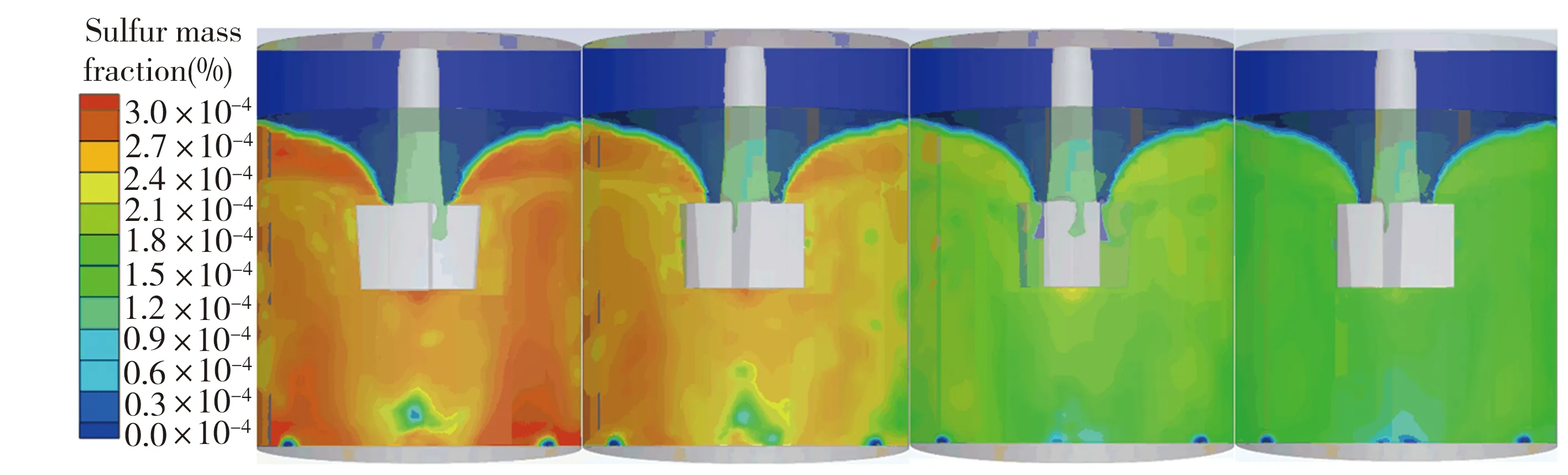
(a)60 s (b)90 s (c)120 s (d)150 s

根據寶鋼生產經驗可知,鐵水平均脫硫率須達到95%,故按照95%的脫硫率計算總投入鐵水包的脫硫劑質量。當鐵水平均硫濃度達到0.0015%時(即脫硫率達到95%)完成脫硫,記錄脫硫劑投放時間。底吹加料與傳統表面連續加料工藝投放脫硫劑質量速率均為3 kg/s,通過投放時間乘以脫硫劑的投放速率得到脫硫劑消耗量。經計算后得到, 通過表面連續加入脫硫劑達到95%的脫硫率需要453 s,共計投放1359 kg的CaO,而采用底噴粉送入脫硫劑達到95%脫硫率僅需要278 s,共計投放836 kg的CaO。由此可見,相較于傳統的表面連續加料工藝,底部噴粉的方式可使脫硫劑使用量減少了約40%,并且顯著提高了脫硫效率。

3 結論

(1) 當脫硫劑噴嘴位置分別設置在距包底中心0.4R、0.6R、0.8R時,脫硫劑上浮時間分別為6、8、12 s,脫硫劑運動半徑依次為0.3R、0.5R、0.9R,表明當噴嘴位置更靠近壁面時,鐵水在底部產生更多旋渦,能夠增加脫硫劑在鐵水包底部弱流區停留時間和運動范圍,并使脫硫劑在鐵水包內分布更均勻,從而降低脫硫劑的凝并程度。

(2) 相較于傳統KR法表面連續加料的方式,采用底噴粉加料方式有效解決了KR脫硫時脫硫劑在鐵水中先凝并后反應的問題,提高了脫硫劑的使用效率。在達到95%脫硫率的情況下,相較于表面連續添料的方式,底噴粉添料使脫硫劑使用量減少了約40%。