基于灰色理論的船舶溢油風險評估方法

馬 峰

(集美大學 航海學院，福建 廈門 361021)

0 引 言

海上原油運輸主要風險是海上溢油事故，原油泄漏不僅嚴重影響了海洋生態和環境，也造成嚴重的經濟損失[1]。

因此，提高海上船舶溢油事故的評估能力，及早對溢油事故進行預防，并建立合理的船舶溢油風險評估方法非常必要。本文系統分析海上原油運輸船舶的溢油風險和要素，結合灰色理論模型建立船舶溢油風險評估方法，對于改善當前原油運輸船舶的安全性，降低船舶溢油風險有重要意義。

1 船舶溢油風險因素分析

結合行業內大量的統計數據，將原油運輸船舶的溢油風險因素劃分為人為因素、海況因素、船型因素和其他因素這4個維度，并針對每個溢油風險維度的特點進行了詳細介紹。

圖1為船舶溢油風險要素的整體占比情況圖。

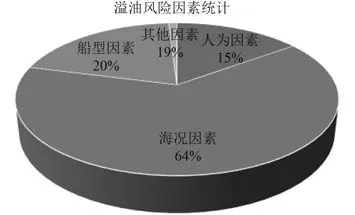
圖1 船舶溢油風險要素的整體占比情況圖Fig.1 Figure of the overall proportion of risk factors of ship oil spill

1）海況因素

海況因素是導致船舶發生溢油事故的最主要原因，海況因素又包括風浪流等自然條件因素和航道條件等硬件因素。

①自然條件因素

海上自然條件非常惡劣，尤其是遠洋和深海區域。一方面，劇烈的海風、海浪可能導致船舶結構的破壞，產生嚴重的燃油和貨物油泄漏；另一方面，劇烈的風浪會誘發和加劇船舶溢油事故造成的破壞作用，對海洋環境的破壞性推波助瀾。

②航道條件等硬件因素

港口、內河航道等硬件條件的限制也可能導致船舶出現溢油事故，比如航道內水深、礁石等因素導致的船舶擱淺事故。此外，良好的導航設備和系統也是保障船舶航行安全的重要措施，能夠從船舶避碰策略、傳感器等方面提升船舶航運安全。

2）船型因素

從港口及航道統計數據分析得知，船型因素在船舶溢油事故中占據的比例僅次于海況因素，船型因素又包括船舶的類型，比如單殼船還是雙殼船、船舶的噸位等。通常，單殼船由于撞擊等事故很容易發生船體破損，導致燃油泄漏，雙殼船甚至多殼船當發生事故時具有一定抗破壞能力，發生溢油事故的風險會明顯低于單殼船。

船舶的噸位與燃油泄漏事故也是呈正相關的關系，隨著船舶噸位的增加，船舶的吃水深度更深，船舶方向改變、速度控制等靈活性都會降低，從而使船舶整體的操作性較差，在港口、內河航道等水域內發生事故的概率更高。

3）人為因素

主要是指船舶操作人員因為誤操作或者疏于職守等原因，導致船舶未按照合理的航線行駛，發生擱淺事故。或者在船舶會遇過程中，操作人員轉向或減速不及時，造成船舶碰撞事故，進而導致船舶燃油的泄漏[2]。

4）其他因素

造成船舶溢油風險的其他因素包括交通密度等因素，隨著交通密度的增加，船舶發生碰撞事故的概率也在不斷增加。統計數據表明，海事事故的發生與距離海岸的距離存在正相關。

圖2表示為不同離岸距離下不同風險因素造成的船舶溢油事故統計。

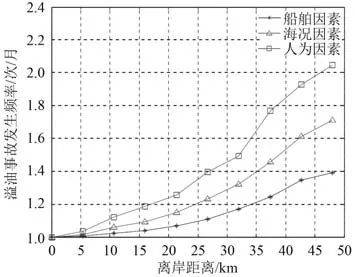
圖2 不同離岸距離下不同風險因素造成的船舶溢油事故統計Fig.2 Statistics of ship oil spill accidents caused by different risk factors at different offshore distances

2 基于灰色理論的船舶溢油風險評估方法

2.1 灰色理論建模

20世紀80年代初，鄧聚龍等率先提出灰色系統理論，該理論將客觀事物理解為不斷變化且相互關聯，并根據客觀事物的未知性將系統分為灰色、黑色和白色系統3種。其中，灰色系統理論主要針對不確定性問題的分析，這種應用場景通過對原始數據序列的建模，從離散的數據中尋找數據序列相互關聯的規律，進而進行非線性系統的建模和預測。

灰色系統模型從數學原理角度上講是一種非線性的數列模型，在利用灰色系統理論進行系統的分析時，首先需要對系統的原始數據進行轉化，將數據轉換為n階矩陣。

在工業控制系統中存在著許多非線性因素，這些因素會不同程度的影響系統的控制精度。采用灰色系統理論并通過定義非線性系統的灰導數等，可以有效對控制系統的變量進行轉化，因此，灰色系統理論的應用范圍很廣。

灰色系統理論的通用工作流程如圖3所示。

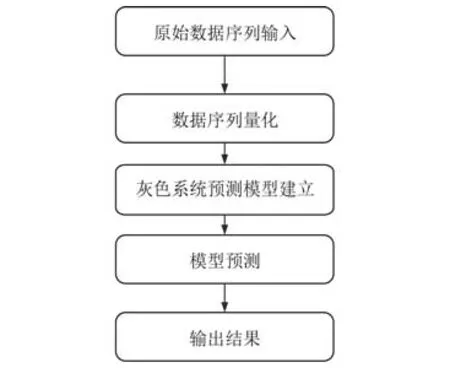
圖3 灰色系統理論的通用工作流程Fig.3 General workflow of grey system theory

灰色理論系統建模過程如下：

1）結合不確定系統的輸入信息，建立原始數列[3]：

2）定義系統的灰導數為：

3）建立灰色理論模型微分方程為：

4）將微分方程的解集轉化為時間序列，從而得到理論模型為：

式中：a，b為理論模型的因數。

2.2 船舶溢油風險評估的灰色理論模型建模

在使用灰色理論對船舶溢油風險進行評估時，根據系統的初始輸入，分別建立系統的因素集和評價集[4]如下：

1）因素集

其中，U1,U2,...,Un分別為人為因素、海況因素、船型因素和其他因素。

2）評價集

V1,V2,...,Vn分 別為船舶溢油風險指標的等級，如V1=表示溢油風險的可能性在10%，20%等。

設溢油評估系統因素集U=(U1,U2,...,Un)中，uij表示因素Ui，Uj的相對重要性，得到如下判斷矩陣：

矩陣的特性包括：

建立溢油風險評估矩陣為：

式中：Ai為指標權重；Ri為隸屬度。

將因素集和評價集矩陣視為時間t的連續函數，建立灰色系統理論模型：

式中：α0為模型的平滑性控制參數；。得到船舶溢油風險評估的響應模型為：

圖4為基于灰色理論的船舶溢油風險評估過程。

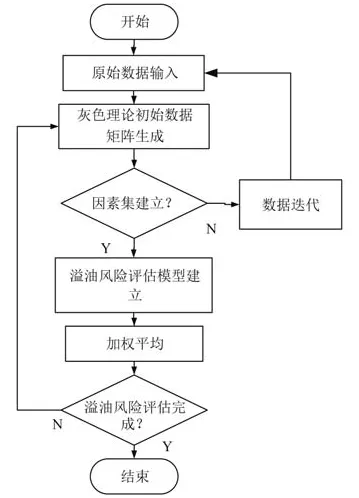
圖4 基于灰色理論的船舶溢油風險評估過程Fig.4 Risk assessment process of ship oil spill based on grey theory

2.3 船舶溢油風險評估與預測

為了驗證本文開發的船舶溢油風險評估方法的準確性，以大連海區的統計數據為基礎，假設大連海區內的船舶碰撞、擱淺等事故符合二項概率分布[5]，大連海區溢油事故統計歷史數據如表1所示。

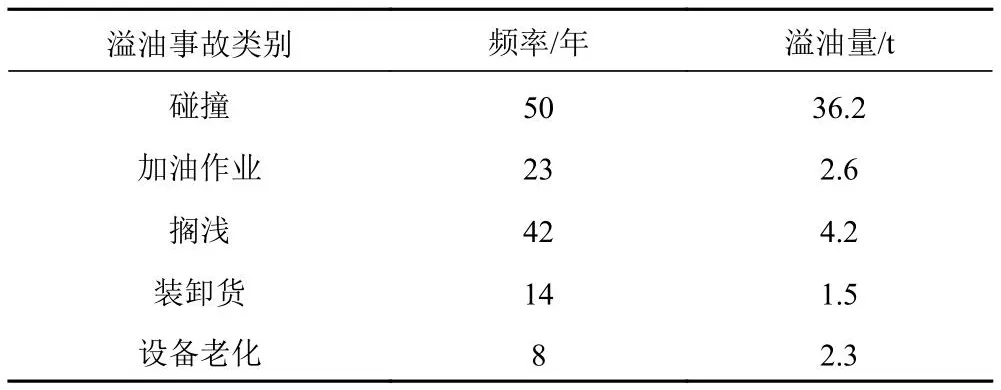
表1 大連海區溢油事故統計歷史數據表Tab.1 Dalian Sea oil spill accident statistical historical data table

本文得到基于灰色理論模型的一年內海域內船舶溢油量的預測數據如圖5所示，可以發現預測結果和實際溢油的誤差在可接受范圍內，因而本文建立的模型具有一定的應用價值。

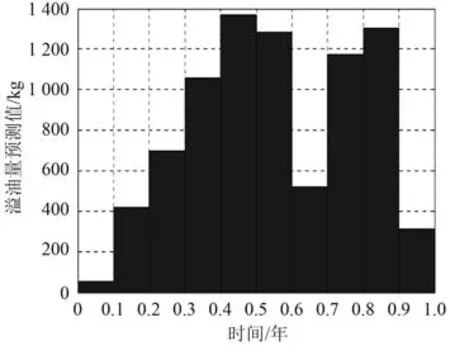
圖5 一年內海域內船舶溢油量的預測數據圖Fig.5 Forecast data of ship oil spills in the sea area in one year

3 結 語

海上船舶的溢油事故對海洋環境有嚴重破壞作用，也不利于船舶的航運安全，本文結合灰色理論原理，建立一種船舶溢油風向評估方法，介紹了評估原理和過程，并針對大連海區的溢油風險進行了預測。