小小“點”,大作用
游淑溶
尺規作圖是初中階段重要的幾何作圖方法。面對平行四邊形作圖題,當你手中只有一把無刻度的直尺時,你是否感到手足無措呢?不要急,這時候我們可以借助平行四邊形的對稱中心這個小小“點”,讓它來發揮大作用。
一、小小“點”牽手角平分線
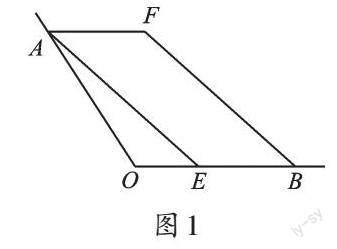
例1 如圖1,已知∠AOB,OA=OB,點E在OB邊上,四邊形AEBF是平行四邊形,在圖中畫出∠AOB的平分線。(只用無刻度的直尺作圖,請保留畫圖痕跡,不寫作法。)
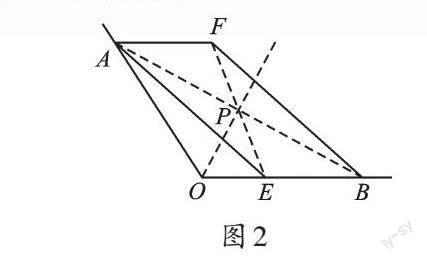
【分析】我們平時用圓規和直尺很容易作出已知角的平分線,但這道題要求用無刻度的直尺作角的平分線,也就是說只能借助直尺連線,該如何畫呢?從題目中的已知條件OA=OB,我們發現,兩條有一公共端點的線段(不在同一直線上)長度相等,說明存在等腰三角形,其實就是作等腰三角形頂角∠AOB的平分線。因為沒有圓規和量角器,所以不能直接作角平分線,只能從其他方面出發。我們知道等腰三角形的頂角的角平分線、底邊上的中線及底邊上的高線是互相重合的,那么我們就可以從底邊AB出發。而四邊形AEBF是平行四邊形,我們不難看出AB是[?]AEBF的一條對角線,也就知道了AB的“雙重”身份,即AB既是等腰三角形的底邊,又是平行四邊形的對角線。這樣我們就很容易想到平行四邊形的對稱中心這個特殊的點了。我們把它看成等腰三角形的底邊AB上的中點,再用無刻度的直尺連接點O和小小“點”即可。
解:如圖2,連接AB、EF,交于點P,射線OP即為所求。
二、小小“點”圓夢相等線段
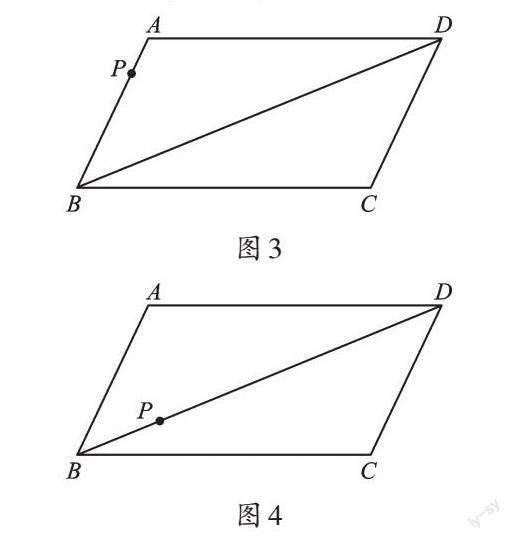
例2 已知BD為[?]ABCD的對角線,請僅用無刻度的直尺分別按下列要求畫圖。(保留畫圖痕跡。)
(1)如圖3,點P為AB上任意一點,在CD上找一點Q,使CQ=AP。
(2)如圖4,點P為BD上任意一點,在BD上找一點Q,使DQ=BP。
【分析】(1)我們知道平行四邊形是中心對稱圖形,點A與點C、點B與點D關于小小“點”(對稱中心)對稱,線段AB與CD也關于它中心對稱。明白了這一點,我們不難發現,這題就是找點P關于小小“點”的中心對稱點。(2)在平行四邊形的對角線上如何作相等的線段?其實我們可以借助第(1)問的方法,由于點P在對角線上,點A、點P所在直線與邊BC有交點(設為點M),所以我們找出點M關于小小“點”O的對稱點N,線段CN與BD的交點就是我們要找的點。
解:(1)如圖5,點Q為所作。
(2)如圖6,點Q為所作。
在解決與平行四邊形有關的作圖題時,我們可以嘗試從平行四邊形的對稱中心入手,發揮這個小小“點”的作用,輕松解決平行四邊形中用無刻度的直尺作圖的問題。
(作者單位:江蘇省泰州市姜堰區城西實驗學校)

