巧用“中心”分空地

徐小冬

我們知道三角形的穩定性在生活中被廣泛運用，如自行車車架、籃球架、三腳架、斜拉橋等，而平行四邊形的不穩定性也大有用處，如電動伸縮門、折疊傘棚、伸縮晾衣架等。平行四邊形有三角形所不具備的中心對稱性，那么平行四邊形的中心對稱性在生活中又有什么樣的妙用呢？下面，我們通過實例一起感受一下。

例題 如圖1所示，甲、乙、丙為小區的三塊空地，為美化小區環境，小區物業決定分別將三塊空地進行綠化。要求用一條直線將每塊空地分成面積相等的兩塊地，一塊用來種花，一塊用來種植綠色植被，特邀本小區居民提供設計方案。

愛動腦的小明結合近期所學中心對稱圖形的相關知識，設計了如下方案。

甲地設計方案：

方法一：利用特殊點或特殊位置（如圖3）。特殊點（矩形的頂點）：直線AC或BD；特殊位置（矩形各邊中點）：直線EF或GH。

方法二：利用矩形的中心對稱性（如圖4）。過矩形對稱中心的任意一條直線平分矩形面積。

我們不難推斷，對于任意的中心對稱圖形，經過對稱中心的任意一條直線平分圖形的面積。因此，今后我們平分圖形面積時，應先考慮它是否是中心對稱圖形，如果是，只要找到它的“中心”即可。但在生活實際中，我們遇到的也不都是中心對稱圖形，對于非中心對稱圖形的面積平分問題，又該如何解決呢？

乙地設計方案：

對于非中心對稱圖形，解決問題的關鍵在于能否將非中心對稱圖形轉化成中心對稱圖形。

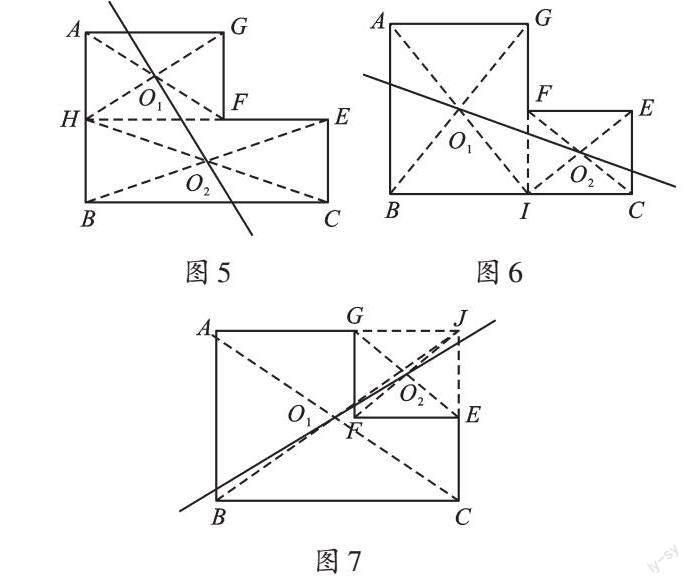
方法一：如圖5、圖6，利用“割”的方法將非中心對稱圖形（多邊形ABCEFG）分割成兩個中心對稱圖形（矩形AHFG和矩形HBCE或矩形ABIG和矩形FICE），找出兩個中心對稱圖形的“中心”O1、O2，則直線O1O2將原非中心對稱圖形（多邊形ABCEFG）的面積平分。

方法二：如圖7，利用“補”的方法將非中心對稱圖形（多邊形ABCEFG）補成兩個中心對稱圖形（矩形ABCJ和矩形EFGJ），找出兩個中心對稱圖形的“中心”O1、O2，則直線O1O2將原非中心對稱圖形（多邊形ABCEFG）的面積平分。

其實，通過“割”或者“補”尋找“中心”的方法具有局限性，即“割”或者“補”所得到的兩個圖形也必須都是中心對稱圖形。如果其中一個圖形不是中心對稱圖形，那又該如何解決呢？

如圖8、圖9，若通過簡單的“割”“補”，則無法平分△CFG的面積。我們可以利用本題EF∥BC這個條件，通過“等積”轉化，將非中心對稱圖形轉化為中心對稱圖形。

如圖10，過CF中點H作BE的平行線，交EF的延長線于點M，交BC于點N，連接EN、BM，交點為O。∵EF∥BC，H為CF中點，∴△CHN≌△FHM，即S△CHN=S△FHM，∴S四邊形BNME=S四邊形BCFE。則過O點的任意直線（直線必須與邊EF相交）將四邊形BCFE的面積平分。

數學源于生活又應用于生活，像小明這樣巧用“中心”設計平分空地方案的生活實例還有很多。我們只有學會用數學的眼光觀察現實世界，用數學的思維思考現實世界，用數學的語言表達現實世界，數學學習才會更有價值和意義。

（作者單位：江蘇省泰州市姜堰區白米初級中學）