含未知控制方向的多智能體系統輸出同步控制

陳宇翔,彭鈞敏

(1.義烏工商職業技術學院 建筑工程學院,浙江 義烏 322000;2.湖南工業大學 電氣與信息工程學院,湖南 株洲 412007)

由于多智能體的廣闊應用背景,自21世紀以來,多智能體的協同控制引起了控制界的廣泛關注。早期的相關工作聚焦于具有線性模型的個體,或一階非線性個體。目前,多智能體系統中個體模型是非線性系統的情形正在為研究者所關注,如分數階系統、鏈式系統、隨機系統、下三角系統、非標準三角系統、歐拉—拉格朗日系統和具有準單側李普希茨非線性動力學的系統等。此外,不確定性和擾動可以更準確地反映系統實際情況,包括不可測的速度信號、輸入約束、未建模的動態以及隨機擾動等情形也被同時考慮在內。當多智能體系統中個體為高階系統且含有不確定性時,目標將從狀態一致變更為輸出同步。高頻控制增益的符號,即控制方向,直接決定了控制是正反饋還是負反饋,對于系統的性能十分重要,已有的研究通常假設其符號為正,而在某些實際系統,如艦船姿態控制、硬盤伺服系統中,其符號是未知的,因此,在控制方向未知條件下如何對系統進行控制就成為了一個難題。Nussbaum[1]提出用Nussbaum函數處理未知控制方向的基礎上,Jiang等[2-7]的研究逐步將這一方法推廣應用至高階非線性系統,且考慮未知參數等情形。隨著多智能體系統研究的深入,Peng等[8-12]逐步將此類未知控制方向的系統模型引入到多智能體系統中,以考慮其協調控制問題。

相較于現有研究成果[9-12],筆者研究取消了對未知控制方向的諸多假設和限制,即智能體可以有不同且相異的控制方向,而控制器的設計并不需要提前知道控制方向的相關先驗信息。在傳統李雅普洛夫函數構造中,Nussbaum函數會在求導之后出現[3-5],筆者構造了一種新型的分析函數,即Nussbaum函數直接出現在分析函數中,而非其導數,不僅可以簡化證明過程,而且可以擴大此方法的適用范圍。

1 預備知識與問題描述

1.1 預備知識

1.1.1 符號定義

在筆者研究中,Rm×n表征i實矩陣。M≥(≤)0表示M是正(負)半定矩陣,M>(<0)表示M是正(負)定矩陣。Null(M)表示矩陣M的零空間,sup(·),inf(·)分別表示最小上界和最大下界,符號sing(·)是經典的符號函數。對于連續可微函數f:Rn→R,行向量?f/?x為[?f/?x1,?f/?x2,…,?f/?xn]。

1.1.2 圖論相關知識

加權圖用G=(V,E)表示,其中V={1,2,…,N}是一個由n個節點組成的非空有限集合,邊集E?V×V被用來描述智能體之間的通信。其中節點i的鄰居集用Ni={j|j∈V,(i,j)∈E}表示。j?Ni意味著不存在節點j到節點i的路徑。一系列邊{(i,k),(k,l),…,(m,j)}代表存在一個節點i到節點j的路徑,對于無向圖來說,如果對于任意節點i,j∈V,存在由節點i到節點j的路徑,則稱該圖是聯通的。

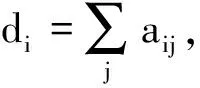
1.1.3Nussbaum函數

Nussbaum函數是具有下列性質的函數,表達式為

(1)

常用的Nussbaum函數包括ek2cos(k),k2sin(k)和k2cos(k)等。

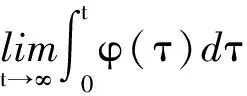
1.2 問題描述

1.2.1 已知條件

考慮一個由n個個體組成的多智能體系統,個體i的模型表達式為

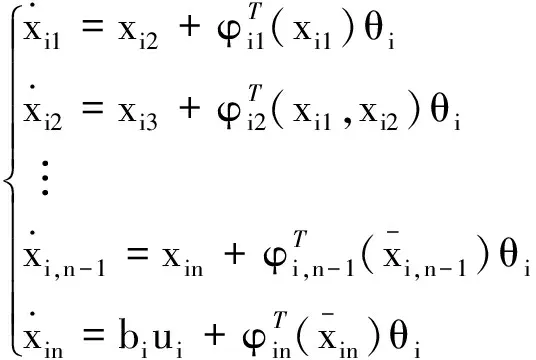
yi=xi1i=1,2…n

(2)

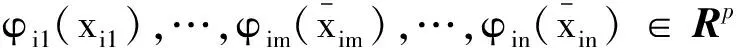
1.2.2 控制目標

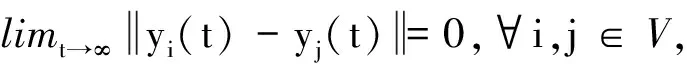
2 控制器設計

對于模型如式(2)的個體i,設計分散控制器,其表達式為

(3)

(4)

其中

(5)

其中a2,a3,…,an>0;函數φim,wim,ψjm表達式分別為

(6)

參數估計器更新率計算式為

(7)

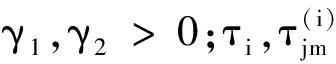
(8)

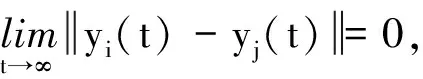
3 理論證明

第一步:定義

(9)

可得Vi1沿式(2)的導數為

(10)

進一步,將式(10)改寫為

(11)

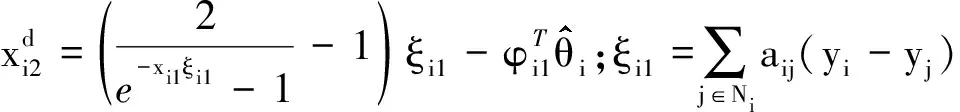
(12)

(13)

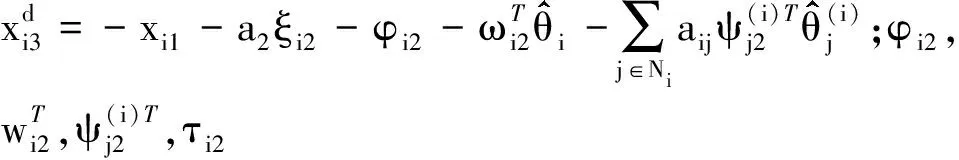
(14)

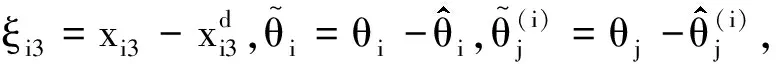
(15)

通過式(12,14),有

(16)

式中γ1,γ2>0為控制增益。

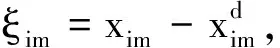
(17)

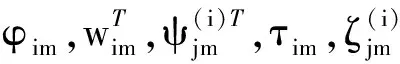
(18)

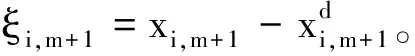
(19)

可得

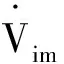
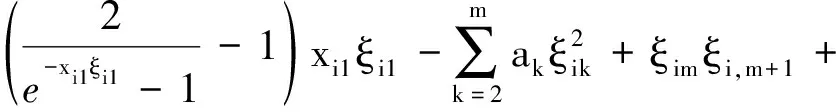
(20)

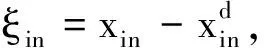
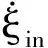
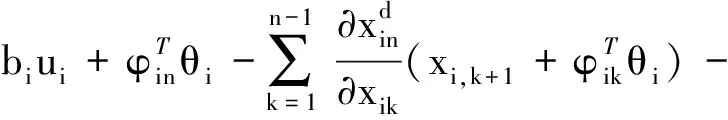
(21)

定義

(22)

注意到

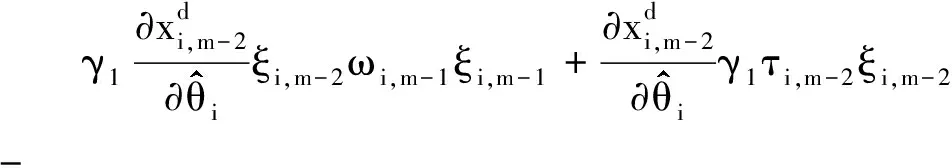
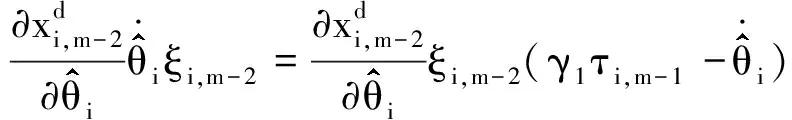
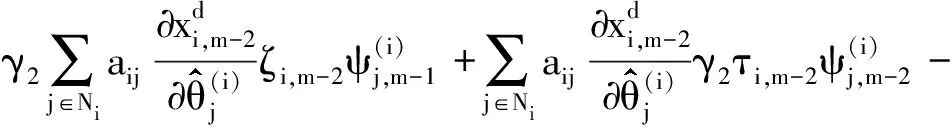
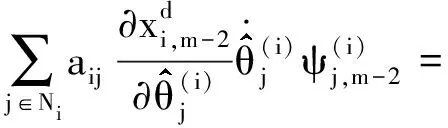
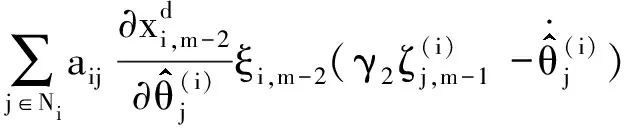
(23)

Vin的導數為

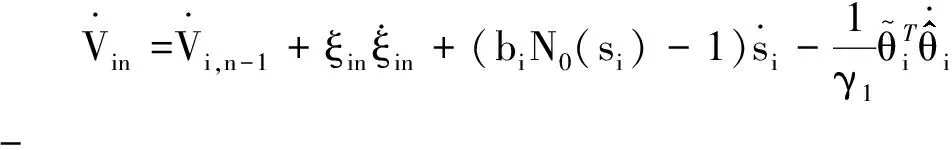
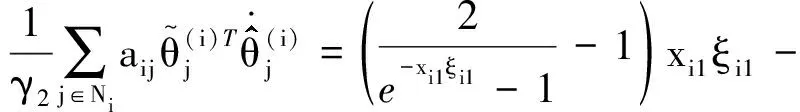
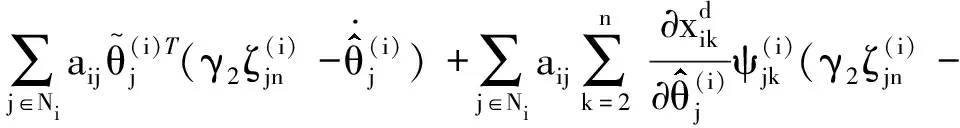
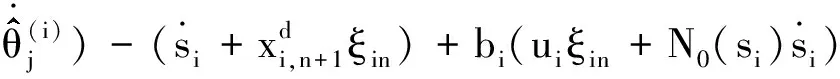
(24)

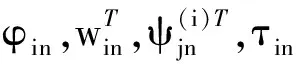
(25)

接下來,將采用反證法證明時間區間[0,+∞)上閉環系統解的存在性。

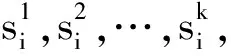
(26)

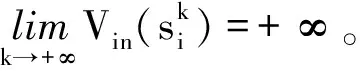
(27)

此外

(28)

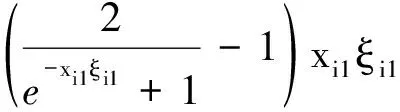
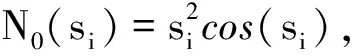
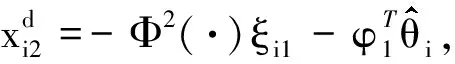
4 仿真結果

通過一個仿真案例來驗證筆者提出的控制器的有效性。考慮一組3個個體的輸出同步問題,個體在圖1中用‘1～3’表示。為了簡單起見,當aij>0時,將aij設置為1。個體i的動態模型為

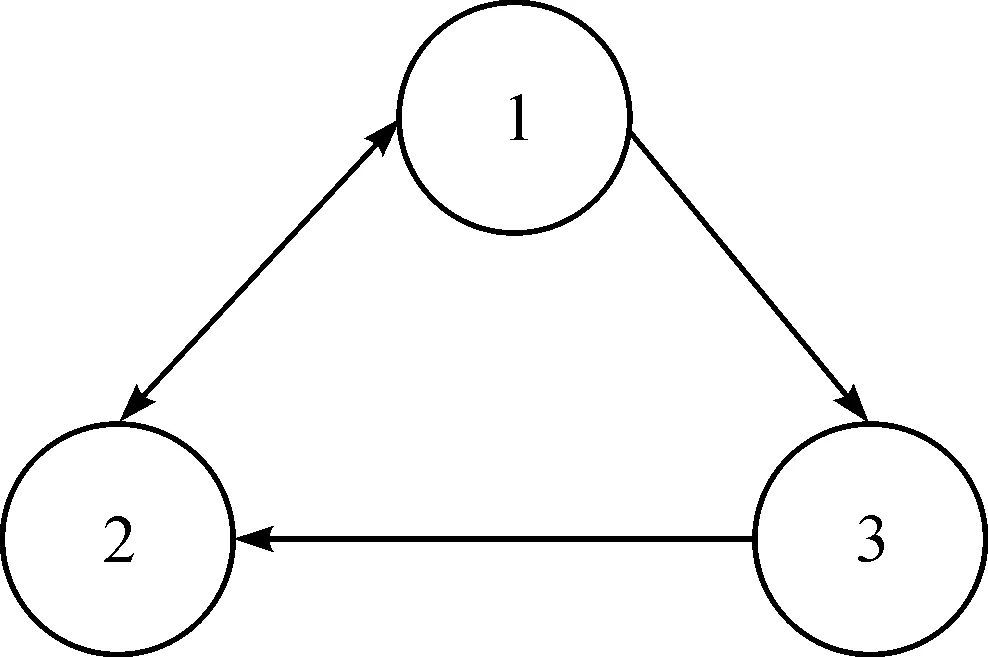
圖1 多智能體系統通信拓撲圖

(29)

對于xi=[xi1,xi2]T,yi和ui分別為個體i的狀態、輸出和輸入;不確定參數bi的符號代表控制方向,同樣未知;θi為未知參數。

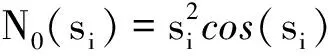
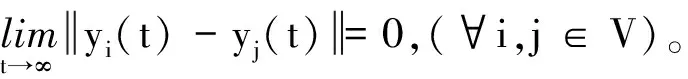
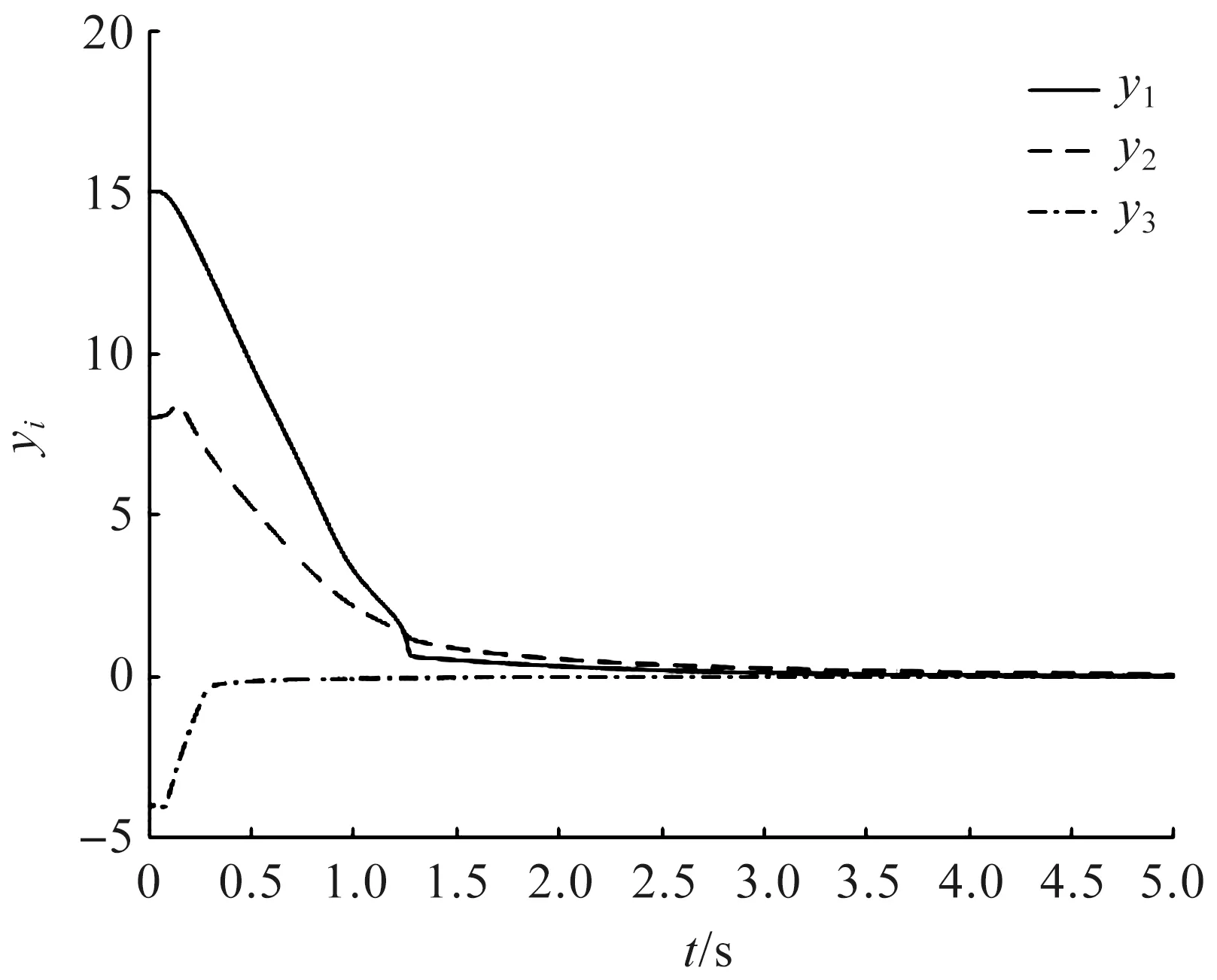
圖2 個體輸出軌跡yi(t)(i=1,2,3)

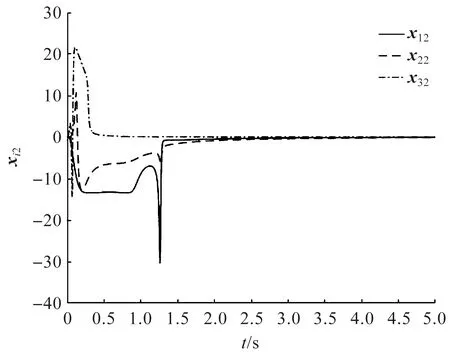
圖3 個體狀態xi2(t)(i=1,2,3)

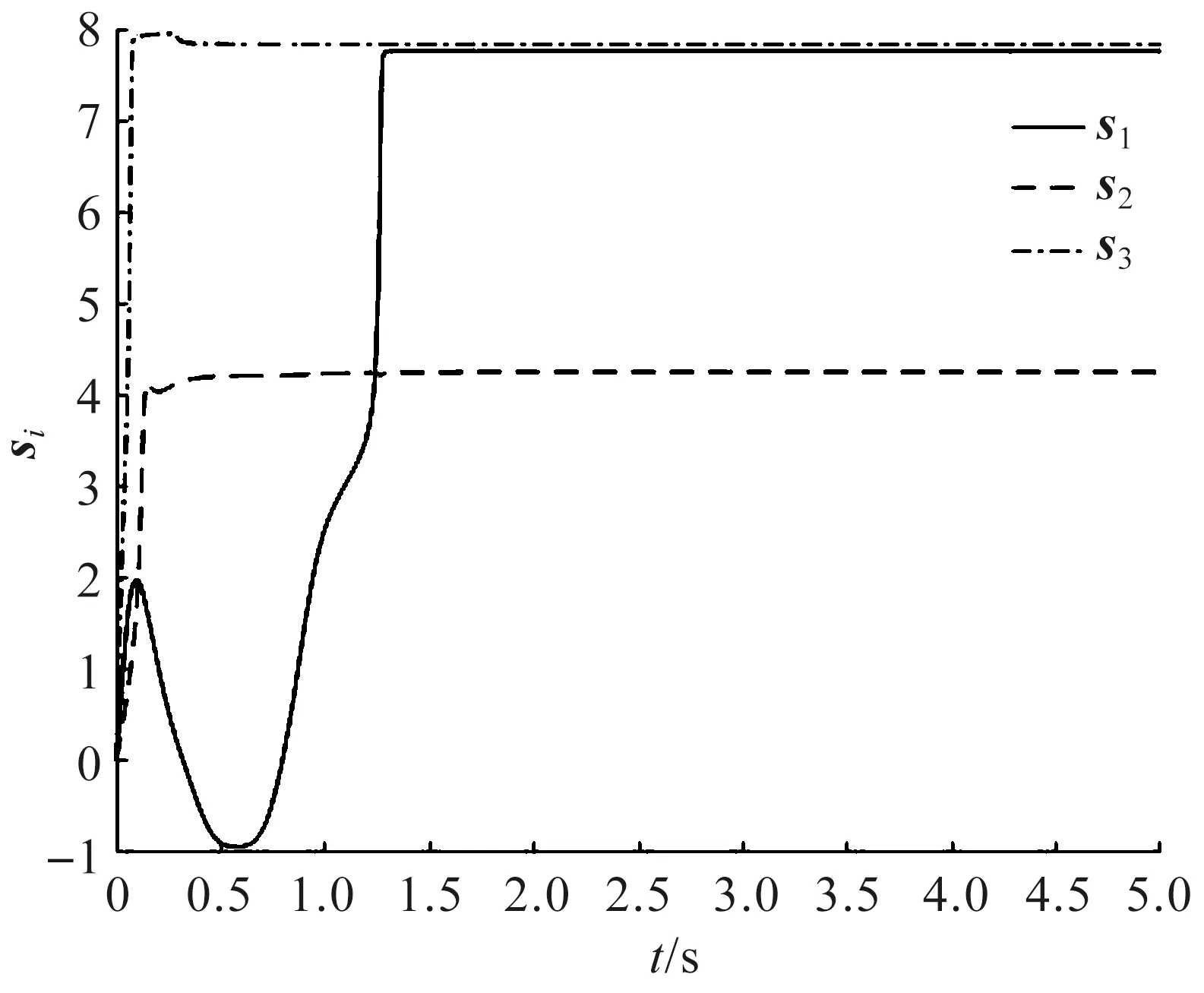
圖4 狀態量si(t)(i=1,2,3)

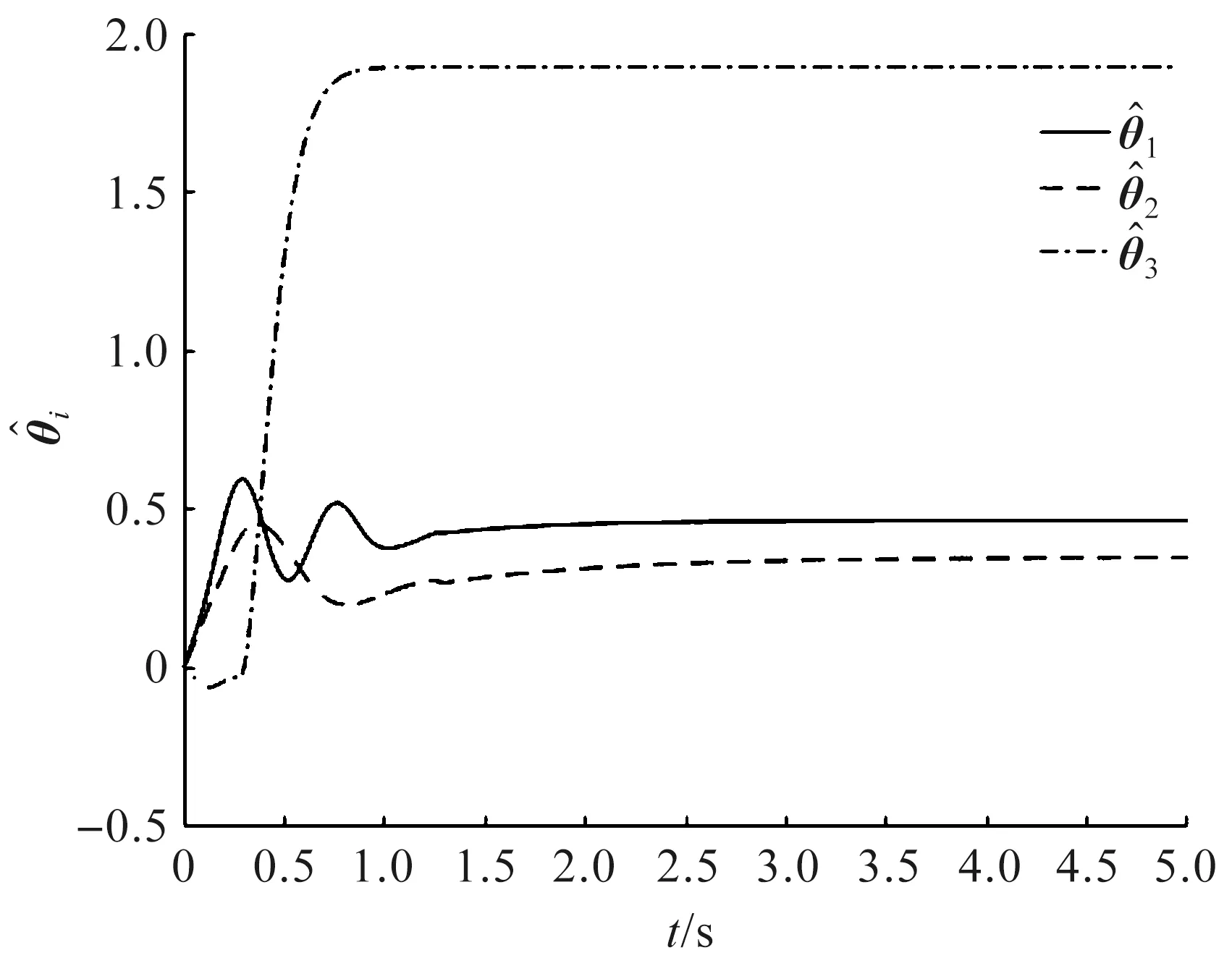
圖5 參數估計器

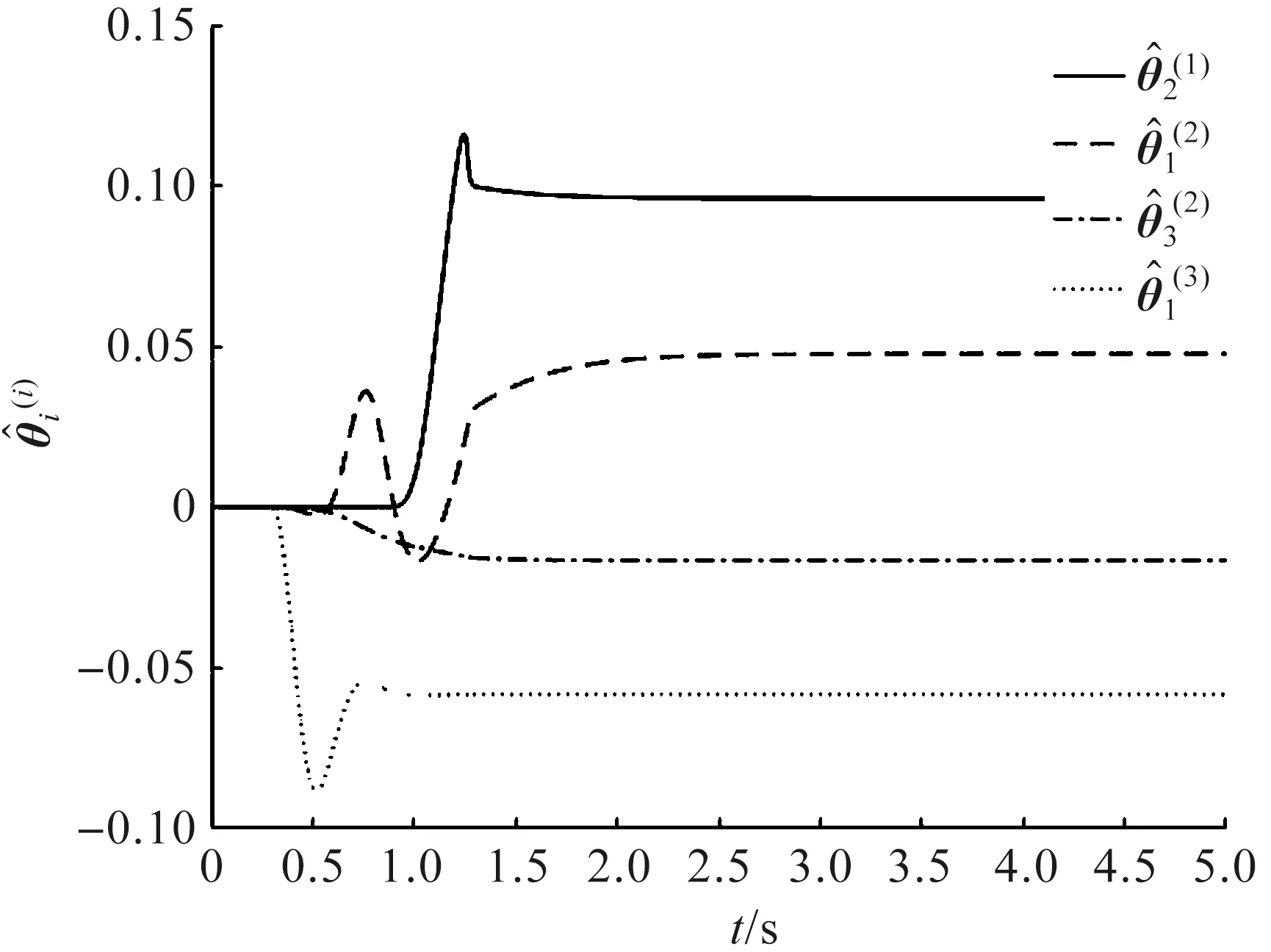
圖6 參數估計器

筆者未來的研究方向將聚焦于這種具有時變延遲的多智能體系統的收斂速度[18]和非嚴格反饋形式的個體模型[19]。

5 結 論

筆者研究了具有參數不確定性和未知控制方向的多個嚴格反饋系統構成的多智能體網絡系統的輸出同步問題,其中通信拓撲為有向圖結構。首先,為每個個體用反推方式設計了一個分散控制器,在實現輸出同步的同時保證整個系統有界;其次,提出了一種新的分析函數構造方法,即Nussbaum函數項直接出現在分析函數本身,而不是其導數中,從而可以簡化證明過程。仿真案例表明了筆者方法的有效性,后期將應用至超級電容儲能系統,以實現故障模式(即發生某些超級電容單體極性反轉)下的電壓均衡控制。