中國古代數學的圖騰:趙爽弦圖

張維忠 唐慧榮

(浙江師范大學教育學院 321004)

大家一定都聽過“大禹治水”的故事吧．“大禹治水十三載,三過家門而不入．”家喻戶曉的他是如何成功治水的呢?趙爽在《周髀算經注》中這樣提到:“禹治洪水,決流江河.望山川之形,定高下之勢.除滔天之災,釋昏墊之厄,使東注于海,而無浸溺.乃勾股之所由生也．”大禹治水竟然與著名的勾股定理有關,是不是有些出人意料呢?

一直以來,勾股定理作為“千古第一定理”,是浩瀚無垠的數學海洋中不可缺失的一顆耀眼明珠,在幾何學科中舉足輕重．它的神秘面紗吸引了廣大的數學愛好者,不同的民族對其都有著獨特的探索．目前,世人對其證明的方法已達500多種．在我國,那不得不提及的就是著名的“趙爽弦圖”．趙爽到底是如何證明勾股定理的呢?下面,我們一起來探究華夏文明中這顆幾何學的璀璨明珠——趙爽弦圖．

1 什么是“趙爽弦圖”

1.1 中國勾股定理的最早記載——《周髀算經》

在中國古代,人們把手臂彎曲成一個近似直角時,靠近肩膀的那部分就叫做“勾”,靠近手的那部分便叫做“股”．一般來說,“勾”的長度小于“股”的長度．西周初年,商高在與周公旦的對話中提到“勾廣三,股修四,徑隅五”．后人簡單地稱之為“勾三股四弦五”,這便是“勾股定理”的雛形．它如何產生的呢?

大約在4 000多年前,黃河流域洪水為患,洶涌的洪水淹沒了田地和房屋,百姓苦不堪言,部落治水九年卻得不到成效．善良的大禹不忍看到百姓飽受水害之苦,他吸取前人的經驗,利用“左準繩,右規矩”進行測量,走遍了山山水水,終于治水成功!咆哮的河水失去了以往的兇惡,百姓的日子變得安定．大禹在此所用的“準繩”和“規矩”就是我國最早的測量工具．簡單地說,準繩是定平、畫直線的工具,可以用來檢測水平和垂直．規矩則分別用來畫圓形和方形．

圖1 《周髀算經》書影

大禹是如何利用這兩個工具的呢?《周髀算經》(圖1)中提到,大禹是利用了“勾廣三,股修四,徑隅五”(32+42=52)的原理來進行距離的計算、規劃并劃分九州以達到疏通河道的目的的[1]．

對于32+42=52,這是勾股定理的一個特例,也是勾股定理在中國的最早記載．追根溯源,勾股定理是我國古代數學發展的重要起源,中華數學傳統中的精髓開方術、方程術等都與勾股定理密切相關．我們知道,數學是一門嚴謹的科學,任何結論的提出都必須經過一步步的邏輯推理．因此,定理的發現是一回事,但對其進行嚴格的證明更是一件了不起的事．千百年來,人們被它的魅力吸引,對此定理的證明趨之若鶩．目前,它是世界上已知證明方法最多的數學定理之一,但在《周髀算經》中尚未發現直接的相關證明．

1.2 中國數學界的圖騰——趙爽弦圖

我國最早對勾股定理進行證明的是三國時代的趙爽(約182—250)．趙爽是我國三國時代的數學家、天文學家．早在公元3世紀左右,他在為《周髀算經》作注釋時,便撰寫了《勾股圓方圖說》一文,介紹了“勾股圓方圖”(圖2)．這幅圖也就是著名的“趙爽弦圖”(圖3)．

圖2 勾股圓方圖 圖3 趙爽弦圖

圖4 第24屆國際數學家大會會標

“趙爽弦圖”被人們稱為“中國古代數學的圖騰”,它簡約美觀而不失深厚,是數形結合思想的典型體現．圖形呈中心對稱,內部是由4個全等直角三角形圍著一個小正方形形成,外部則是將這4個三角形的頂點連接成一個大正方形．一直以來,“趙爽弦圖”在數學人心中的地位非同小可．我國著名數學家華羅庚曾建議用一幅反映勾股定理的數形關系圖來作為與“外星人”交談的語言．2002年第24屆國際數學家大會會標(圖4)就依此制作．讓我們想象一下,這個古老而飽含智慧的圖案是不是還像一個轉動著的風車?它透露著中國人民熱情友好的民族特色[2]．

那趙爽是如何記載的呢?他在《周髀算經注》中寫道:“勾、股各自乘,并之為弦實.開方除之,即弦．”你們能看懂這句古文的意思嗎?

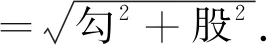
這樣來看趙爽所記載的內容就是大家所熟悉的勾股定理“原貌”.在初中教材中,一般把勾股定理簡單表述為:直角三角形兩直角邊的平方和等于斜邊的平方．

作為一條古老的數學定理,勾股定理包含著中國古代厚重的文明,它的出現和發展對于發揚古代數學文化起到了重要作用．縱觀數學史,它不僅為幾何學奠定了基礎,它衍生的許多分支也都得到了廣泛的應用,對數學學科的發展有著深遠的影響．比如,在中學數學學習中“利用數形結合,把直角三角形的特征轉化成三邊的數量關系”,勾股定理就與之密切相關．

2 趙爽弦圖與勾股定理

對于利用趙爽弦圖來證明勾股定理,目前有兩種比較主流的方法:一種是數學史家錢寶琮(1892—1974)解讀的“代數證明”,另一種是數學史家李文林提出的“出入相補”[3]．

2.1 “趙爽弦圖”與“代數證明”

我們跟著錢寶琮先生一起來解讀趙爽弦圖吧．

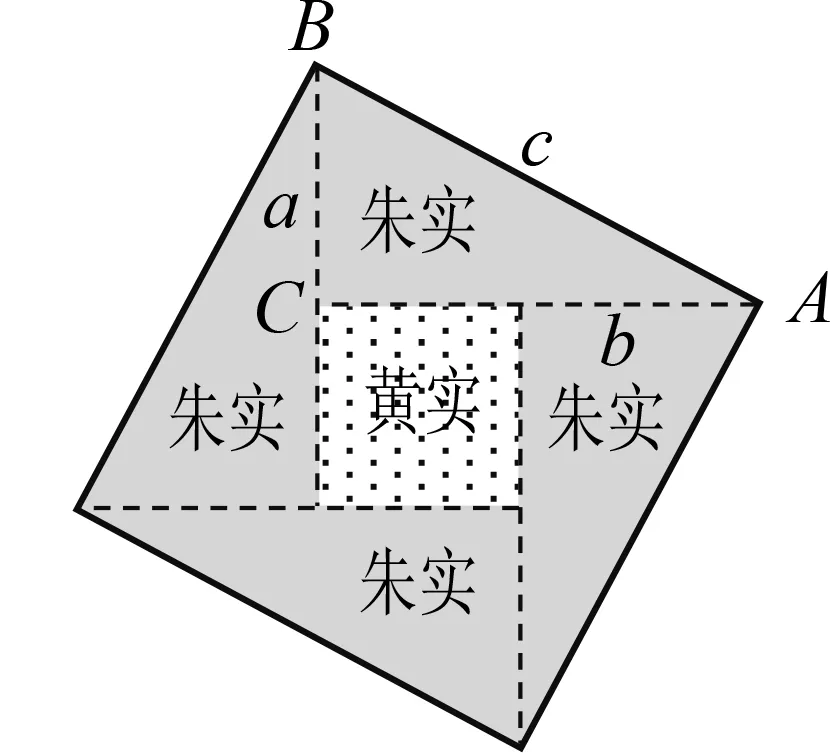
圖5 弦圖

觀察弦圖(圖5),圖中的4個全等直角三角形涂上了朱色,其面積被稱為朱實;中間的1個小正形涂上黃色,其面積被稱中黃實．趙爽寫道:“按弦圖,又可以勾、股相乘為朱實二,倍之,為朱實四.以勾、股之差自相乘,為中黃實.加差實,亦成弦實．”

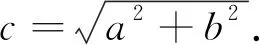
值得指出的是,在弦圖原圖中,雖然趙爽畫的是邊長為3,4,5的直角三角形,但其證明不失一般性,可見古代中國在數學上的成就不同凡響．

2.2 “趙爽弦圖”與“出入相補”

數學史家李文林認為,趙爽是利用了“出入相補”的原理來證明勾股定理的．“出入相補”原理,顧名思義,就是對圖形進行分割再移補而解決問題的方法．對此,有沒有似曾相識的感覺呢?在平面圖形面積計算的教學中,我們就是利用“轉化”的數學方法進行公式推導,如將三角形進行分割拼成長方形后進行面積公式的推導,這就是出入相補的應用．

在總面積相等的條件下,先對兩個正方形進行分割,根據需要移動補湊,對分割后的圖形進行位置上的變動,就這樣達到了證明勾股定理的目的．如圖6(1),根據一個直角三角形的兩條直角邊a,b為邊長的兩個正方形畫出的一個合并圖形,面積為a2+b2;再如圖6(2)這樣,截下兩個直角邊分別為a和b的全等三角形,并且將這兩個直角三角形旋轉至圖6(3),這樣就得到一個以原三角形之弦為邊的正方形,其面積應為c2．根據變化前后總面積不變,得到a2+b2=c2．在中國傳統數學中像這樣運用“出入相補”原理證明數學命題的方法十分普遍．

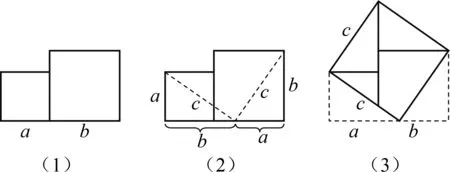
圖6

以上兩種對趙爽弦圖的解讀代表了中國古代數學以形證數、數形合一的特點,這種代數與幾何之間密不可分的特色在世界數學史上獨樹一幟．

2.3 穿越古今,感受數形結合的魅力

看了以上的兩種證法,如果給你提供以下2個活動材料(圖7),你能像古人一樣運用自己的智慧感受一下數形結合的證明過程嗎?

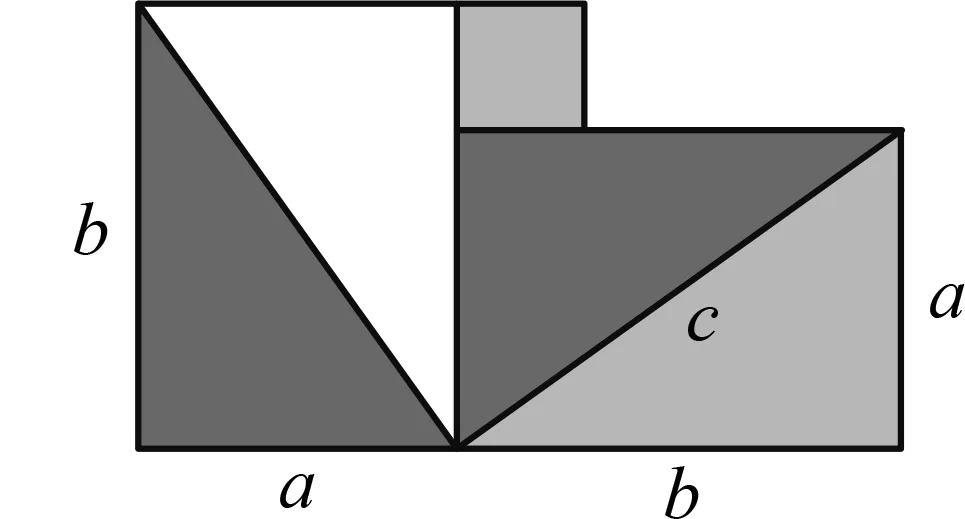
圖7

活動1 探究趙爽弦圖的證明

在白紙上先畫出圖7,再剪下試試．如果碰到困難,可以借助以下三條線索進行解決．

線索1 對比趙爽弦圖,利用提供的材料進行拼圖實驗．

線索2 每一塊區域的面積分別怎樣表示?它們之間有怎樣的關系?

線索3 趙爽弦圖還有其他的解讀方法嗎?你可以利用網絡等資源進行了解和探索．

活動2 探究畢達哥拉斯學派的證明

勾股定理作為世界的共同文化遺產,受到了全世界的重視．西方人們相信它是由古希臘思想家、數學家畢達哥拉斯(約前580—約前500)在公元前500年發現的,故稱之為“畢達哥拉斯定理”．畢達哥拉斯學派從鋪地磚問題中發現勾股定理(圖8、圖9),但由于學術的秘密性及歷史年代的久遠,他對勾股定理的證明并沒有流傳下來．畢達哥拉斯是怎樣發現勾股定理,又用了什么方法證明?后人對其做了合乎情理的推測．

圖8 圖9

請你完成下列任務,試著進行證明．

(1)請仔細觀察圖10,完成下表．

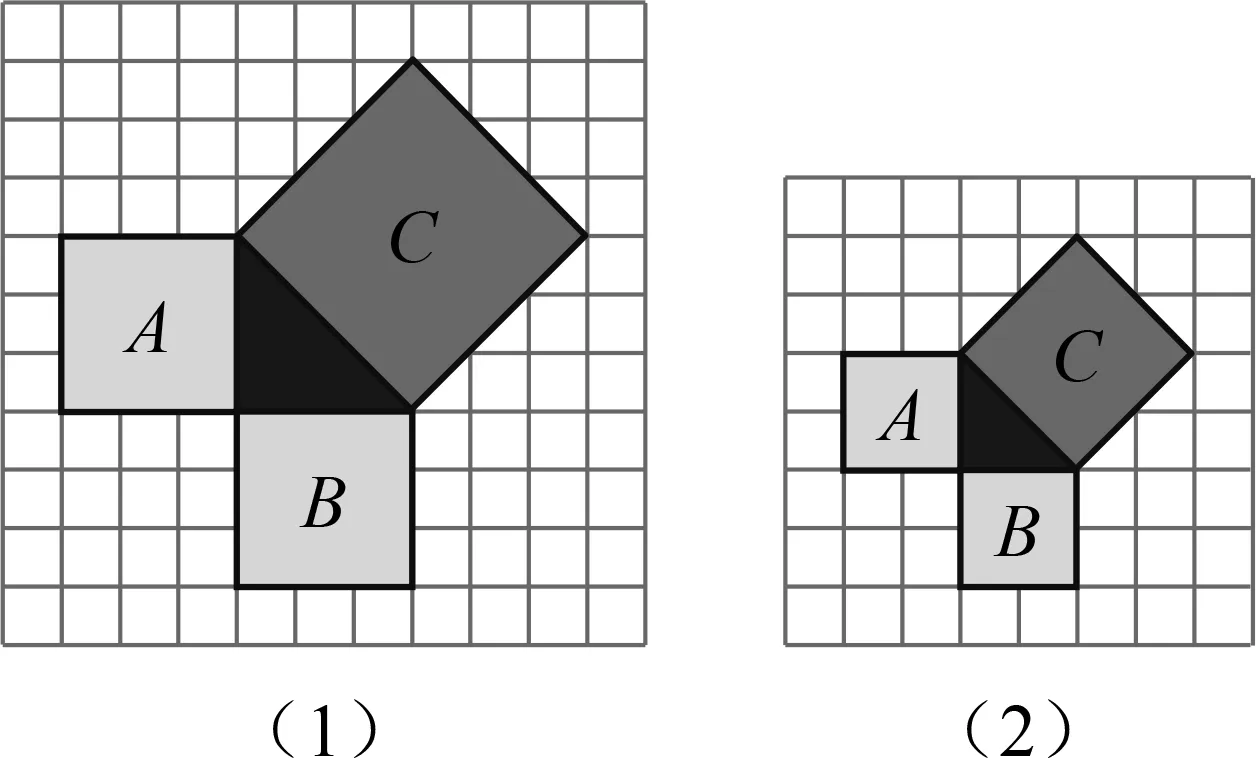
圖10

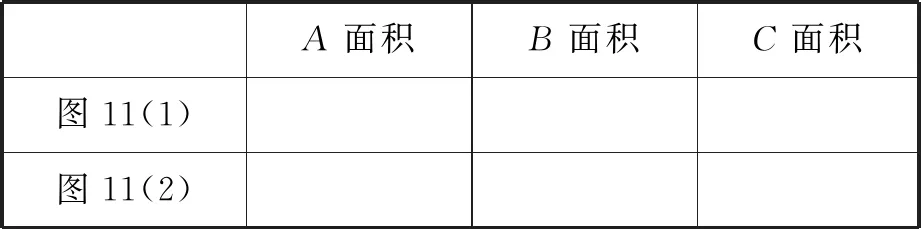
A面積B面積C面積圖11(1)圖11(2)

(2)你有什么發現呢?

(3)畢達哥拉斯發現了三角形直角邊上的兩個正方形合起來的面積等于斜邊上的大正方形的面積．你同意他的說法嗎?

對比兩種方法,你更喜歡哪一種?

(待續)