鐵路梁式橋震后通行能力評估

目前已有的地震易損性研究主要著眼于結構震后破壞概率，而對結構震后使用性能的評價則少有涉及。提出了一種通過地震易損性分析進行鐵路梁式橋震后通行能力評估的方法：選取橋梁合理位置的地震響應，建立與軌道平順度指標間的映射關系，再根據平順度指標確定通行能力評估等級，基于所確定的指標與分級標準可以得到平順度易損性曲線。以2座典型鐵路梁式橋為案例，基于Abaqus軟件建立有限元模型，通過非線性時程分析獲得結構地震響應，繪制易損性曲線并進行通行能力評估。結果表明：所提方法建立的平順度易損性曲線可以用于評估鐵路梁式橋的震后通行能力；軌道高低平順度是控制鐵路梁式橋整體通行能力的關鍵指標，可以作為鐵路橋梁震后修復和結構優化的主要方向之一。

鐵路橋; 通行能力; 易損性; 平順度

U445.7+5 A

［定稿日期］2022-02-22

［作者簡介］范樂雯（1997—），女，碩士，研究方向為現代橋梁橋式結構理論。

1 通行能力評估

1.1 線路平順度

經由十余年大規模的快速建設，我國高速鐵路運營里程已穩居世界第一，這嶄新的歷史階段也對當前高速鐵路的長期安全運營提出了更高期望。高速鐵路軌道質量狀態對列車運行的舒適性和安全性有著不可忽視的影響，是限制行車速度的主要因素。并且軌道不平順將加劇輪軌間的動力相互作用，增加列車與軌道結構損耗，導致其維修周期和使用壽命縮短，使行車條件惡化，甚至造成列車脫軌。

高速鐵路對軌面的高平順性有著近乎嚴苛的要求。當前各國的高速鐵路軌道不平順管理主要包含局部幅值管理和區段質量管理，以局部幅值管理為主［1］。我國現行的鐵路線路維修規則中，也針對普速鐵路、高速鐵路有砟和無砟軌道的動態不平順劃分了偏差等級和容許偏差管理值。此外，高速列車系統運行的平穩性與舒適性受到高速鐵路基礎結構服役性能的直接影響，需要額外關注路基、橋梁等下部結構的平順度。目前國內高速鐵路普遍采用無縫鋼軌［2］。地震作用下，鐵路橋發生橫向和豎向的變形變位，主梁與軌道的變形會受到彼此約束影響，使橋梁地震響應映射到軌面，由此產生的軌道不平順一旦超限，將對列車系統運行造成困擾。

1.2 通行能力等級

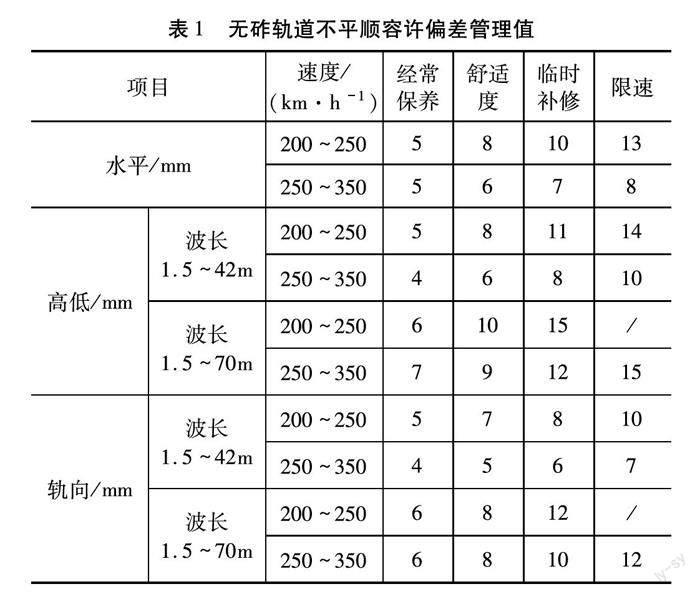
《鐵路線路維修規則》［3］中，軌道動態不平順偏差等級劃分為四級：Ⅰ級為經常保養標準，Ⅱ級為舒適度標準，Ⅲ級為臨時補修標準，Ⅳ級為限速標準。高速鐵路無砟軌道線路水平、軌向和高低的容許偏差管理值見表1。其中，在限速等級下，200～250 km/h線路列車行駛速度需下降至160 km/h，250（不含）～350 km/h線路列車行駛速度需下降至200 km/h。

參照《鐵路線路維修規則》的條文內容，對鐵路橋震后通行能力等級劃分見表2。列車處于舒適度等級時，全速運行會降低車內旅客乘坐舒適度，但對震后的物資運輸與搶險救災行動影響極小。列車處于修補等級時，在軌道經過及時修補后可以保持原速運行，該等級在日常運營維護中作為軌道整修的質量控制標準，對列車系統運行影響小，但在震后救災情形下需考慮臨時修補的必要性與所耗費時間。列車處于限速等級時，需控制運行速度并及時進行軌道修補以維持運行平穩性，在恢復至平順度要求前將影響列車系統運行效率。

1.3 易損性分析方法

地震易損性分析作為當前評估結構抗震性能的一種途徑，通過得到地震強度與結構失效概率間的關系，可以輔助判斷結構在地震下的預期損害或同類結構的潛在震害。易損性曲線可用于表現結構的地震易損性，其橫軸為表示地震

動強度的指標，縱軸為達到地震損害等級或破壞極限狀態的結構響應超越概率。因此，可以采用易損性分析與建立易損性曲線的方法評估鐵路橋震后通行能力。

通常，為評估橋梁震后的損傷水平，可以選取反應結構抗震能力的指標，按照地震烈度等參數對橋梁破壞狀態分類，進行橋梁地震易損性分析并形成結構易損性曲線［4］。同理，評估鐵路橋震后通行能力時，可以選取反應列車系統運行功能的指標，按照鐵路線路對平順度偏差等級的劃分，進行鐵路橋線路平順度的地震易損性分析并建立鐵路橋震后通行能力易損性曲線。

建立易損性曲線所采用的2類方法：經驗方法需要收集大量往期地震資料，進行可靠度分析；理論方法則可采用數值模擬進行較為精確的計算，且可使用簡化方法來提高計算效率。對鐵路橋震后通行能力的評估可以采用理論方法建立易損性曲線。

2 通行能力易損性

2.1 易損性指標

通過易損性分析的方法來評估地震后鐵路橋通行能力所受的影響，需要選取反應地震動強度的指標，以及表征軌道平順度、影響列車系統運行功能的橋梁結構參數。有學者以高鐵橋梁的地震易損性評估為目標結果，通過比較橋梁和軌道構件的抗震需求及承載能力，對比了峰值地面加速度（PGA）、譜加速度（SA）作為地震動參數的適用性，相比之下使用PGA可以獲得更保守的易損性曲線［5］。

高鐵簡支梁橋的橋墩震后破壞程度低，震致破壞多集中于梁縫，由支座轉動或移位引起的梁端錯位［6］。連續梁橋的墩柱、橋臺震后破壞程度低，震致破壞多集中于支座處，尤其是橋臺處活動支座［7］。由此可知，地震作用下由支座位移或轉動所引起的軌道不平順，更容易出現在墩臺支座處和跨中位置的鋼軌范圍內。故可選取簡支梁橋梁縫范圍內和連續梁橋支座處上部的軌道不平順值，作為表征高鐵橋梁列車系統通行能力的指標。

2.2 指標映射關系

為定量分析高鐵橋梁列車系統運行功能損失，需確定用于評估的軌道不平順值與易損性分析所用結構響應值間的映射關系。墩臺支座處和跨中位置主梁單元的地震位移響應所對應的軌道不平順值，可以作為鐵路橋易損性分析的計算指標。其中，與梁軌相互作用直接相關的軌道不平順值項目包括水平、高低和軌向。

水平不平順指軌道同一橫截面上左右兩軌頂面的高差，經換算后對應兩軌中線處橋梁結構單元在垂直縱橋向平面內的轉角與標準軌距的乘積。軌向不平順指軌頭內側面沿長度方向的橫向凹凸不平順，常將左、右軌方向的平均值作為軌道的中心線方向偏差，對應兩軌中線處橋梁結構單元在橫橋向位移的波峰波谷之差。高低不平順指軌道沿鋼軌長度方向在垂向的凸凹不平，對應兩軌中線處橋梁結構單元在豎向位移的波峰波谷之差。

綜上，可選取對應主梁單元3方向的地震響應為易損性分析的計算指標。各計算指標與評估指標間映射關系見表3。其中，順橋向為X軸，豎向為Y軸，橫橋向為Z軸。

2.3 易損性曲線

采用理論方法建立地震易損性曲線，首先需要建立地震需求概率模型：將橋梁的有限元模型與所選取的各條地震波荷載數據組合，采用有限元軟件對各組數值模型進行非線性時程分析，從而計算得到各條地震波荷載下反應橋梁需求的響應值［8］。地震需求概率模型以回歸模型的形式表示橋梁地震需求與地震動強度之間的關系，則易損性指標對應的地震需求可以表示為式（1）。

SD=a·IMb（1）

式中：a和b為回歸系數，IM為地震動強度參數。基于地震動強度值與非線性時程分析所得到的各組響應值，對2組數據進行回歸分析，可以得到地震需求概率模型的回歸系數a和b，從而確定易損性指標地震需求的表達式。

基于橋梁地震需求的回歸模型，以及各通行能力等級的平順度指標限值，可以通過對數正態累積概率密度函數，計算鐵路橋震后達到各級通行能力等級的超越概率見式（2）。

Pf=φln（Sd/Sc） β2d+β2c（2）

式中：Sd為平順度指標通過映射關系對應的地震需求值；Sc為各級通行能力等級對應的平順度指標限值； β2d+β2c為復合對數標準差，自變量選用PGA作為地震動強度參數時，取值為0.5［9］；φ［·］為標準正態分布函數，均值為0，方差為1。將式（1）取對數后代入式（2），可以得到以地震動強度為自變量的超越概率函數，見式（3）。

Pf=φb+a·ln（x）-ln（Sc）β2d+β2c（3）

若需分析整個結構系統的易損性，則應通過整合結構中各構件的易損性來得到結構系統的易損性曲線。基于第一可靠度原理可以確定系統易損性的上界和下界［10］，其中下界是各構件易損性的最大值，上界是各構件易損性的組合值。同理，為得到橋梁整體平順度易損性，可將各平順度指標的易損性進行整合，則通過上、下界確定的橋梁整體平順度易損性表示為式（4）。

max［P（Fi）］≤P（Fsys）≤1-∏mi=1［1-P（Fi）］（4）

式中：P（Fsys）為整體易損性，P（Fi）為某一指標的易損性。通過上界對系統易損性評估得出的結果偏于保守，因此在分析橋梁整體的平順度易損性時，選擇上界作為評估的依據更為合適。

3 案例評估

3.1 數值模型

選取一座典型鐵路簡支梁橋、一座典型鐵路連續梁橋作為評估對象，并應用有限元軟件ABAQUS建立橋梁模型。簡支梁橋為無砟軌道預應力混凝土雙線簡支梁橋，計算跨度為31.5 m。連續梁橋為無砟軌道預應力混凝土雙線連續梁橋，計算跨度為（48+80+48） m。2座鐵路橋的線路最高設計時速均為350 km/h，適用于地震動峰值加速度Ag≤0.2g地區，故選取Ag=0.2g。

為保證地震動數量充足，地震隨機性得到充分模擬，從太平洋地震工程研究中心（PEER）強震記錄數據庫中選取符合場地與橋型設計要求的22條歷史地震動，并通過系數調整分為5個級別，以及縱橫向2個方向，總計220條地震波作為輸入激勵進行地震時程反應分析。

采用ABAQUS對各條地震波與橋梁模型的組合進行非線性時程分析選取位于跨中與墩支座處4條鋼軌位置下方的橋面單元節點，提取所需指標對應的結構地震響應值： UR1平面轉角、U2豎向位移和U3橫向位移。基于指標映射關系對各組模型的3項響應值進行換算處理，再與對應的地震動強度進行回歸分析，得到表4中各組地震概率需求模型的回歸系數，從而確定各平順度指標的地震需求值Sd。

3.2 分析評估

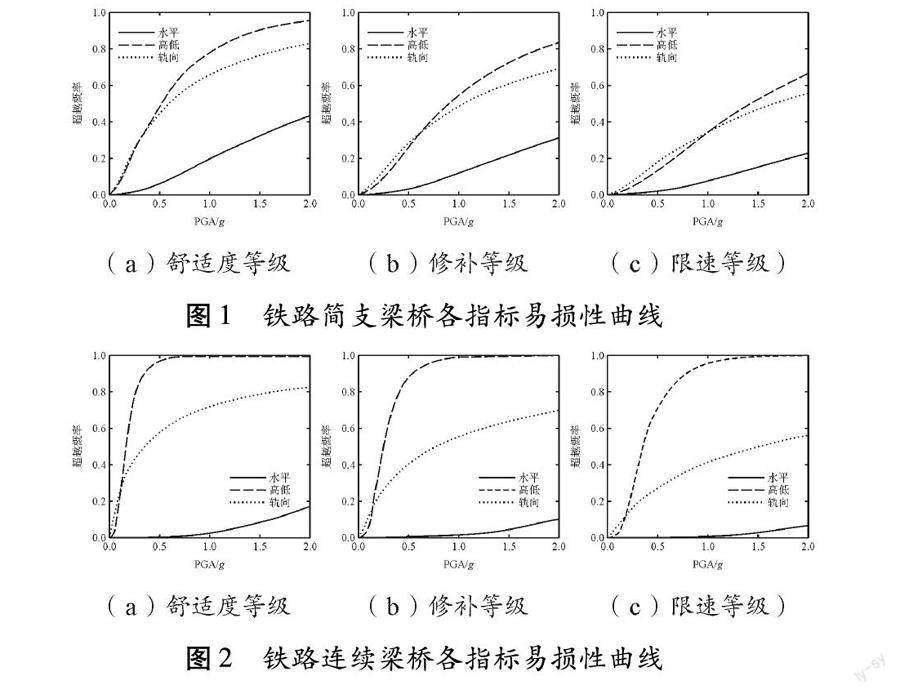
案例所選鐵路橋橋型為計算跨度31.5 m的簡支梁橋和（48+80+48） m的連續梁橋，列車運行速度均為350 km/h，據此可選取表5中用于評估鐵路橋震后通行能力的平順度指標分級限值。基于表格所確定的鐵路橋各級震后通行能力值Sc，以及數值模擬計算得到的地震需求值Sd，按照式（3）繪制出鐵路簡支梁橋和連續梁橋各平順度指標的易損性曲線，橫坐標為地震動峰值加速度PGA（g），縱坐標為橋梁震后達到各通行能力等級的超越概率。

圖1、圖2為鐵路簡支梁橋和連續梁橋在各通行能力等級下3項指標易損性曲線。通過對比同一等級下各指標的易損性曲線可得出，高低和軌向2項指標的易損性曲線增長速度始終高于水平指標。在地震動強度較低的范圍內，軌向易損性略高于高低易損性，但隨著地震動強度的增加，高低易損性曲線的增長速度開始高于軌向易損性并最先達到峰值，水平易損性則始終處于相對較低水平。

可通過式（4）整合2座橋梁在各通行能力等級下3項指標的易損性，獲得其概率范圍的上界作為鐵路橋在該等級的系統易損性曲線。圖3為鐵路簡支梁橋和鐵路連續梁橋的整體平順度易損性曲線。從左到右依次為舒適度等級、修補等級和限速等級。簡支梁橋的平順度易損性在1g后開始處于較高水平，連續梁橋的平順度易損性在0.3g后開始處于較高水平，超過該強度的地震有較大概率導致2座鐵路橋震后通行能力降低。簡支梁橋的舒適度等級易損性曲線在0.6g前增長迅速，在其后曲線趨于平緩且峰值出現在1g之后；修補等級和限速等級易損性曲線在0.1g和0.2g后增長均較快。連續梁橋的舒適度等級易損性曲線在0.3g前增長迅速，在其后曲線趨于平緩并在0.7g時達到峰值；修補等級易損性曲線在0.4g前增長迅速，在其后曲線趨于平緩并在1g時達到峰值；限速等級易損性曲線在0.5g前快速上升，在其后曲線開始趨于平緩且峰值出現在1g之后。

對比同一座鐵路橋各級的平順度易損性曲線可以發現，舒適度等級、修補等級和限速等級對應的3條易損性曲線間隔比較均勻，這是因為各通行能力等級定義的平順度限值具有一致的差值。對比同一等級下鐵路橋整體平順度曲線與其3項指標的平順度易損性曲線可以發現，橋梁各級的整體易損性曲線與其高低指標的易損性曲線十分接近，這是由于3項指標中高低平順度的易損性增長快且最先達到峰值，震后通行能力主要受鋼軌高低平順度的控制。

4 結論

本文提出了一種通過地震易損性分析進行鐵路梁式橋震后通行能力評估的方法，同時選取2座典型鐵路梁式橋的評估案例介紹了這種方法的應用，以期服務于未來鐵路橋梁的震后運行功能評價工作。典型鐵路梁式橋案例的震后通行能力評估結果：①在超過1g和0.3g強度的地震下，鐵路簡支梁橋和連續梁橋的震后通行能力具有較高的易損性；②兩座典型鐵路梁式橋的高低易損性增長快且最先達到峰值，震后橋梁通行能力主要受鋼軌高低平順度的控制。

參考文獻

［1］ 田國英，高建敏，翟婉明.高速鐵路軌道不平順管理標準的對比分析［J］.鐵道學報，2015，37（3）：64-71.

［2］ 闞正明. 地震作用下高速鐵路橋梁軌道變形研究［D］.南京：南京工業大學，2015.

［3］ 高速鐵路無砟軌道線路維修規則 TG/GW 115-2012（試行）［S］.

［4］ H.Hwang，劉晶波.地震作用下鋼筋混凝土橋梁結構易損性分析［J］.土木工程學報，2004（6）：47-51.

［5］ Wei， B.， Li， C. & He， X. The Applicability of Different Earthquake Intensity Measures to the Seismic Vulnerability of a High-Speed Railway Continuous Bridge. Int J Civ Eng 17， 981–997 （2019）. https：//doi.org/10.1007/s40999-018-0347-3

［6］ 國巍，王陽，葛蒼瑜，等.近斷層地震動下高速鐵路多跨簡支梁橋震致破壞特征［J］.振動與沖擊，2020，39（17）：210-218.

［7］ 李立峰，吳文朋，黃佳梅，等.地震作用下中等跨徑RC連續梁橋系統易損性研究［J］.土木工程學報，2012，45（10）：152-160.

［8］ Farahnaz Soleimani， Sujith Mangalathu， Reginald DesRoches. A comparative analytical study on the fragility assessment of box-girder bridges with various column shapes［J］. Engineering Structures，2017，153.

［9］ HAZUS. Earthquake loss estimation methodology. Technical Manual， National Institute of Building for the Federal Emergency Management Agency， Washington （DC）， 1997.

［10］ Eunsoo Choi， Reginald DesRoches， Bryant Nielson. Seismic fragility of typical bridges in moderate seismic zones［J］. Engineering Structures，2003，26（2）.