數形結合 讓思維可視化
——以《數與形》教學為例

文|胡冬南

數學是研究數量關系和空間形式的科學。數學來源于對現實世界的抽象，通過對數量和數量關系、圖形和圖形關系的抽象，得到數學的研究對象及其關系。由于小學生心理的發展特點，小學數學課堂教學以直觀和具象為主，這樣更適合學生對數的感知和認識。因此，數學課堂教學需要讓學生能從具象中抽象出數和關系，使學生獲得良好的數學教育，得到知識、技能，進而逐步形成適應終身發展的核心素養。可見，在一節課中，促進學生的思維進階就尤為重要。下面筆者以《數與形》一課教學為例，談談怎樣通過“數形結合”的方法進行圖解數學，引領學生在讀圖、畫圖、說圖等過程中將思維可視化，進而促進學生的思維進階。

一、《數與形》一課中的思維路徑分析

在人教版數學廣角《數與形》一課中，教材從兩道例題出發，讓學生從例1 的一組圖形中完成填空發現規律，通過例2 畫圖解決算式中的問題。但在以往的實際教學中發現，學生很難在兩道例題的解決中理解和感悟“數形結合”的數學思想，不同學生在學習這節課后的思維水平差異很大，且例2 中“無限”的概念非常抽象。因此，分析清楚這節課學生的思維發展路徑對教學的開展尤為重要。

（一）教材中的教學路徑

（二）學生學習的思維路徑

教材是靜態地呈現學生需要學習的內容，而學生在課堂上學習數學是動態的。所以，有經驗的數學教師不僅要“吃透”教材，而且更重要的是“吃透”學情。在教學前，通過讓學生進行簡單的預習和試做課后習題，發現學生存在“觀察——找規律——應用”簡單地套用“方法”，而不是真正內化方法、掌握方法并學會應用。因此，教師必須對學生學習的思維路徑進行調整和優化，在進行教學設計中，我把本課的教學分為兩大塊內容，即“以數助形”和“以形解數”。

在“用形想數”中通過學生自己舉例子，以自己的例子畫出對應的圖形，把自己的思維通過“畫圖”進行可視化，不同的例子對應不同的圖形，進而形成一組學生“思維可視化”的作品，引導學生發現和內化其中的規律。預設如下：

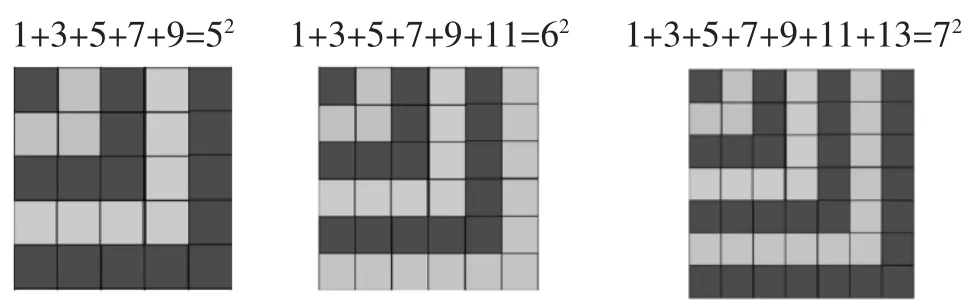
在“用數想形”中通過學生選用“正方形”或“圓”，用不同的畫圖方法來表示算式：把自己對這個算式計算過程的思維進行“可視化”，然后通過對自己的“作品”進行上臺講解，深化學生對數形結合方法的認識，擴展方法多樣性，突出數形結合方法的妙用。預設如下：

這樣，學生學習的思維路徑就變為：

例1：學生讀圖——算式對照——猜想規律——舉例寫算式并畫圖——得出規律

例2：學生觀察——試著計算——畫圖表示——說圖解題——直觀理解——感受極限

正是基于以上分析，我認為本節課的核心不是得出規律和結論，而是讓學生通過“數形結合”的方法，運用“讀圖”“畫圖”“說圖”把自己的思維可視化，通過不同的“圖形”解決方案來感知和體會數形結合的思想，而且在解決數學問題中真正提高學生運用數形結合的意識和能力。此外，通過本節課的教學，讓學生真正感受到學習數學最重要的不是“套用”方法，而是真正地把數學中的知識和方法進行內化并應用，從而做到舉一反三。

二、利用數形結合，在課堂中使學生的思維可視化

數形結合使抽象的數據形象化，使直觀的圖形數學化，從而把握圖形背后的數學本質。

片斷（一）：數形結合，“以數助形”

1.從圖形歸納出算式

師：出示3 個正方形，觀察它們有什么共同特點？

生：都是由若干個小正方形拼成的。

師：你能用一個算式表示小正方形的個數嗎？

生1：乘法算式：2×2（或22） 3×3（或32） 4×4（或42）

師：你還能用其他算式來表示嗎？

生2：加法算式：1＋3 1＋3＋5 1＋3＋5＋7

師：（追問）“1”在哪里？“3”在哪里？請學生上來指一指。這兩種算式有什么關系嗎？

生：它們是相等的。

教師小結并形成板書：1＋3=221＋3＋5=321＋3＋5＋7=42

2.由算式聯想出圖形

學生感知規律，教師啟發：我們由這3 個正方形想到了3 組這樣的等式。如果讓你繼續加上小正方形，像這樣的等式你能寫嗎？試著寫一個并畫出來。

預設如下：1＋3＋5＋7＋9=521＋3＋5＋7＋9＋11=62

1＋3＋5＋7＋9＋11＋13=72

師：現在我們一邊回憶一下這幾個圖形，一邊說一下它們所代表的算式。

3.歸納小結

師：這樣，我們就把算式和圖形對應起來啦！其實，這樣的算式還有很多。請大家一起來觀察它們，你有什么發現嗎？

學生四人小組交流討論，組間補充，得出規律：“從1 開始，幾個連續奇數相加的和等于奇數個數的平方。”

師生小結：通過剛才“讀圖”和“畫圖”，我們發現“數”與“形”是真的有聯系的，用形想數、用數想形、用數形結合的方法在探索形的過程中找到了數的內在特點，幫助我們很快地找到了規律。

教學片斷（二）：數形結合，“以形解數”

1.了解學情

生1：后面一個加數是前面一個的二分之一，也就是“一半”。

生2：加數越來越小了。

師：（追問）這個算式你在哪里看到過嗎？會算嗎？

學生交流討論發言說出自己遇到的困難。

2.自主畫圖，展示說圖

教師出示：一個正方形和還有一個圓，都表示“1”。

要求：任選一個圖形，畫一畫、算一算，記錄你的想法。

預設如下：

生2 敘述畫法：同一個圓的大小取決于圓心角的大小，于是每次取剩下圓心角的一半，第一次是180度，第二次是90 度，第三次是45 度……

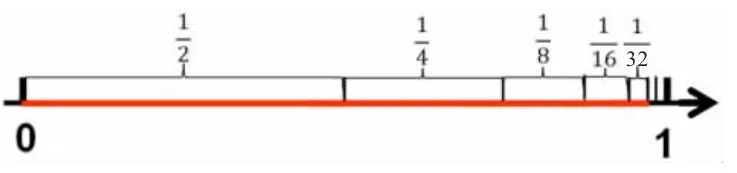
3.歸納小結（略）

三、思維可視化幫助學生思維進階

（一）利用圖解數學，數形結合，深刻體會“數與形”之間的緊密聯系

在課前，通過簡單的課前談話調查，了解學生對于“數與形”的認識，發現學生比較有代表性的兩個觀點:一種是把數與形分隔開來看待，數就是數，形就是形，約占65%；另一種認為“數與形”是有一定聯系的，但具體聯系在哪，學生并不能很好地說明和舉例，約占35%。而在這節課后，我讓學生舉例說明數與形之間的具體聯系（課本中的例子除外），95%的學生能舉出各種各樣的例子，植樹問題中的線段圖、扇形統計圖的百分數、分數乘除法等。

這就說明本節課的教學讓學生深刻地經歷了“數形結合”。通過讓學生深刻經歷數學知識和方法形成的過程，利用圖解數學、數形結合的方法，使學生從圖形中歸納出算式，由算式來聯想出圖形，再自己舉例畫圖，從而體會到數與形之間的緊密聯系，使學生感受圖解數學、數形結合的思維方式，把學生課堂上整個學習思維的過程進行了可視化，促進了學生解決此類問題思維的形成和發展。

（二）通過思維可視化，畫圖說圖，感悟數學思想方法，促使思維進階

“思維可視化”是為了促進認知結構的建構、優化，進一步提升思維能力及思維品質。在《數與形》的教學過程中，利用圖解數學、數形結合的方法，首先讓學生認識到了“數與形”之間密切的聯系，但并不足以建構和優化學生的認知結構，也無法一下子提升學生的思維能力及思維品質。所以，在建構和優化學生的認知結構和提升學生的思維能力及思維品質這兩個方面，都需要更好的“抓手”。通過讓學生從算式出發畫圖，就是在幫助學生把“數形結合”這個方法在自己的認識體系中建構起來，而不同的“畫圖方案”既是學生個體思維可視化的圖解表達，也拓展了群體解題方法的多樣性，從而完成本課知識的內化和方法的建構。

通過個體學生對自己“畫圖作品”的闡述，說圖展示讓群體學生了解不同個體學生思維上的一致性。雖然他們的“畫圖作品”略有不同，但利用圖解數學、數形結合解決問題的思維路徑卻是類似的。而學生個體通過群體學習，在解決同一個問題時，能利用“數形結合”進行方法多樣的圖解來表達，本身就是思維品質的提升，即思維的進階。

這節課在思維進階上，學生從學習《數與形》這一課對知識點的記憶，進而理解數形結合的方法，到應用數形結合的方法去解決問題的低階思維，發展到學生利用“數形結合”的方法去分析問題，用“圖解數學”讓思維可視化去評價，最后自己提出和創造數學問題進行思考的高階思維。