神奇的莫比烏斯

文|鄧亞紅

【教學內容】

北師大版六年級下冊第54、55 頁。

【教學過程】

一、情境導入，認識莫比烏斯帶

1.教學片斷——制作實驗，認識莫比烏斯帶。

師：這是一張長方形紙條，一只螞蟻在紙條的正面，在它的反面有一點面包屑。猜一猜，螞蟻能爬過去吃到面包屑嗎？注意，螞蟻不能爬過紙條的邊緣，也不能撕毀長方形紙條。

生：我覺得螞蟻爬不過去，因為有邊緣擋住了。

生：我覺得螞蟻爬不過去，除非把紙條撕斷。

生：我覺得在紙條的中間穿一個洞螞蟻可以爬過去。

生：我想也許可以爬過去，我們可以用一張紙條嘗試一下。

師：剛才有位同學提供了一個非常好的思路，我們可以試一試，看看會不會有奇跡發生。請同學們在自己的操作紙上模擬實驗一下，要使螞蟻能爬過去吃到面包屑，你有什么好辦法呢？

生：我把這張長方形紙條兩端首尾相連粘貼成一個紙環，螞蟻還是不能爬過去。

師：請你模擬一下螞蟻怎么爬的？

生：請看這里，螞蟻到邊緣就過不去了，因為螞蟻在紙環的一面，面包屑在紙環的另一面。

師：有實驗成功的嗎？

生：我發現螞蟻真的能爬過去。我先把長方形紙條扭轉了180°，然后再兩端首尾相連粘貼成一個紙環。

師：你來證明給大家看。

生：大家跟著我的手指看，螞蟻從這里出發，沿著紙環一直走，能走到面包屑這里。

師：螞蟻真的爬過去了！還有誰能用不同的方法來證明呢？

生：為了讓大家看得清楚一點，我用彩筆描了一下螞蟻爬行的路線，彩筆從螞蟻出發，沿著紙環一直往下畫，就可以到達面包屑的位置。螞蟻真的可以不跨越邊線就能吃到面包屑了。

師：請你來教教大家怎么做到的。

生：先把長方形紙條的一端扭轉180°，再把紙條的兩端首尾相連粘貼起來。

（學生互相學習，動手實驗證明，并把實驗的過程說給同桌聽）

【設計意圖：通過情境導入，充分激發學生探究的興趣，讓學生在猜測中產生解決問題的需要——怎樣改變長方形紙條的形狀，才能讓螞蟻爬過去吃到面包屑？學生通過制作莫比烏斯帶，模擬螞蟻爬行實驗，積累了豐富的活動體驗，感受莫比烏斯帶的神奇和數學的無窮魅力。】

2.教學片斷——對比實驗，探究莫比烏斯帶的特征。

師：剛才你們把長方形紙條扭轉180°做成的紙環，就是數學上說的莫比烏斯帶。

師：同樣是把長方形紙條做成紙環，為什么第一個紙環（普通紙環）上的螞蟻吃不到面包屑，第二個紙環（莫比烏斯帶）上的螞蟻能吃到面包屑？這兩種紙環有什么區別？大家用眼睛看一看，用手摸一摸，或者用彩筆描一描對比研究一下。

生：我用手摸了摸，發現普通紙環有兩個面，一個是里面一個是外面，還有兩條邊。

生：普通紙環粘貼后，長方形的正面與正面相接，反面與反面相接。但莫比烏斯帶粘貼后，正面與反面相接連成一個面了。

生：我用手指滑過莫比烏斯帶，手指經過紙環的每一部分又回到起點。所以我發現莫比烏斯帶只有一個面，而且這個面是一個彎曲的面。

師：這樣彎曲的面叫做曲面，每個同學都試著用手指滑過莫比烏斯帶的曲面，體會一下是不是只有一個曲面。

生：我用彩筆給莫比烏斯帶的曲面描色，從螞蟻開始描起，描過紙環的每一個部分，最后又回到了螞蟻這個起點。我發現莫比烏斯帶的曲面是首尾相連的。

生：我發現莫比烏斯帶的邊也具備這樣的特征，無論從哪個點開始，用彩筆沿著紙環的邊線描一圈，線條不會中斷，描過所有的邊線后又回到了這個起點。所以莫比烏斯帶只有一條邊線。

追問：如果給小螞蟻換個位置，它還能吃到面包屑嗎？

生：可以，因為這個紙環只有一個曲面，無論小螞蟻放在哪里，都能爬到這個曲面的任何一個點上。

小結：普通紙環是雙側曲面，有2 個面，2 條邊線；莫比烏斯帶是單側曲面，只有1 個面，1 條邊線，而且都首尾相連。

【設計意圖：通過對比實驗，讓學生在看一看、摸一摸、畫一畫的實驗操作中，運用不同的策略、從不用的角度探究普通紙環和莫比烏斯帶的區別，充分感受莫比烏斯環帶單側曲面的神奇之處，培養學生用數學的眼光觀察莫比烏斯帶的特征。】

二、剪環實驗，探究莫比烏斯帶等分特征

1.教學片斷———等分紙環，深入了解莫比烏斯帶的特征。

師：把一個莫比烏斯帶從中間畫一條線等分成兩份。如果沿著它的二等分線剪開，會是什么圖形呢？先猜一猜。

生：可能是兩個普通圓環。

生：可能是兩個一樣大小的莫比烏斯帶。

生：也有可能是一個大紙環。

師：我們一起來剪一剪，驗證一下。

師：我們已經沿著莫比烏斯帶的中線剪到這（快要剪完），停下來仔細看一看、摸一摸，想象一下完全剪開后會是什么圖形呢？

生：兩個莫比烏斯帶。

生：兩個普通圓環。

生：一個普通圓環。

生：一個莫比烏斯帶。

師：與上次相比，有了不一樣的猜測。請同學們繼續慢慢地沿著二等分線剪，一邊剪一邊思考，剪開后最終是什么圖形？剪完后，再看一看、摸一摸、描一描，驗證一下。

（學生慢慢剪開，仔細觀察，充分想象，小心求證）

【設計意圖：當快要剪完時停下來，再次引導學生進行二次猜測，意在讓學生體驗數學實驗的科學嚴謹，通過數學實驗培養學生的觀察能力、推理能力，發展空間想象和數學思維能力，加深學生對莫比烏斯帶特征的理解。】

師：剪開后是什么圖形呢？你是怎么驗證的？

生：剪開后不是平均分成兩個環，而是一個大環。

生：我用彩筆描一描，發現它出現了2 個側面。好神奇啊！

生：沿著二等分線剪開，邊線沒有剪斷，但變長了，變成了原來的兩倍長。所以成了一個大環。

生：我用筆描了一下，發現這個大環有2 條邊線，所以它不是莫比烏斯帶。

師：很有價值的思考，他們從面和邊線的角度進行解釋和判斷，發現剪開后不是莫比烏斯帶。

生：沿著二等分線剪開后是一個大環，但它不是莫比烏斯帶，因為它出現了2 個這樣的扭轉。

師：在制作莫比烏斯帶時，我們是把紙條的一端扭轉了1 次。這里紙條扭轉2 次后，為什么就不是莫比烏斯帶呢？

生：扭轉1 次，就是把長方形紙條的一端扭轉了180°，正面與反面連接起來成了一個面，就成了莫比烏斯帶。扭轉2 次，相當于紙條的一端扭轉了360°，紙條是正面與正面連接、反面與反面連接，這樣就與常見的普通圓環一樣有2 個側面，2 條邊。

小結：剛才同學們將一個莫比烏斯帶二等分后剪開，發現它不是一個大莫比烏斯帶。在剛才的學習過程中，我們先大膽猜測，再合理進行實驗操作，在操作中不斷觀察、不斷思考，最后證明自己的猜測是否正確。用這種嚴謹、科學的實驗態度來研究數學知識，是我們學習中非常重要的一個方法。

【設計意圖：這個環節放慢節奏，讓學生在數學實驗中完整地經歷觀察、猜測、實驗、求證的數學“再發現”的全過程，探究二等分莫比烏斯帶的特征，形成科學嚴謹的探究態度，培養有條理的分析、推理能力，發展數學思維。】

2.教學片斷——小組合作，實驗感悟莫比烏斯帶等分規律。

師：剛才同學們沿著二等分線剪開感受了莫比烏斯帶的神奇，如果沿著它的三等分線、四等分線剪開，又會是什么呢？

（學生小組合作，自由猜想，實驗探究，交流方法）

生：沿三等分線剪開后是1個大環套1 個小環。大環不是莫比烏斯帶，小環是莫比烏斯帶。

生：沿三等分線剪開，相當于是一次二等分后的大環加一個與原來一樣的小環，所以小環是莫比烏斯帶。

生：沿四等分剪開，相當于進行了兩次二等分，所以得到2 個大環。

生：沿四等分線剪開后是2個套在一起不能互相分離的大環，但都不是莫比烏斯帶。

生：我發現了一個規律，如果繼續沿著五等分線剪開，應該是先剪出1 個二等分后的大環，剩余的三等分再剪出1 個二等分后的大環和一個與原來一樣大小的莫比烏斯帶。

生：以此類推，是不是可以理解為沿著六等分線剪開，就是3個二等分后的大環，都不是莫比烏斯帶。

生：按照大家的思路繼續想，是不是有這樣的規律，沿著偶數等分線剪開，得到都是大環，都不是莫比烏斯帶；沿著奇數等分線剪開，得到的是若干個大環和1個小環，大環不是莫比烏斯帶小環才是莫比烏斯帶。

生：而且這些環都是套在一起的，永遠不能分離。

師：同學們真的善于觀察、善于思考，通過三等分、四等分剪，并大膽類推出五等分、六等分剪開后的規律，太了不起了。是不是真的有這樣的規律呢，我們一起來看看一段驗證視頻吧。

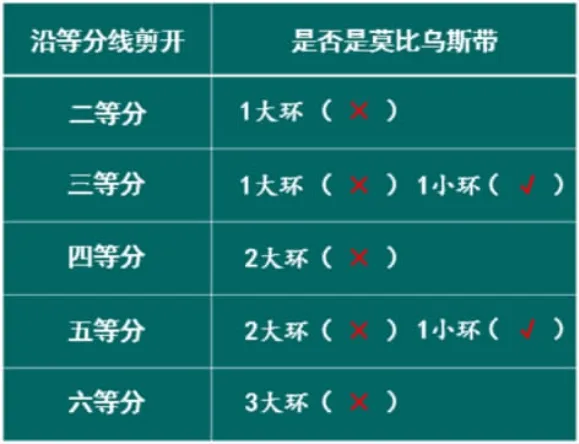
【設計意圖：學生通過豐富的剪環實驗，在觀察、猜測、驗證的過程中積累了充分的活動體驗，掌握莫比烏斯帶三等分、四等分剪開后的特征，并借助這些直觀感受，類推出莫比烏斯帶等分剪開后的規律。通過數學實驗，將抽象的數學知識變得可看可摸，直觀形象。】

師：在日常生活中，也有一些是利用莫比烏斯帶原理設計的物體和現象，如過山車的軌道等。莫比烏斯帶除了今天課內同學們發現的這些特征和規律，課后還可以繼續研究，如果把長方形紙條往不同的方向扭轉，得到的紙環一樣嗎？扭轉180°、360°、540°……分別得到什么紙環呢？期待同學們更多精彩的發現。