頻譜共存下面向多目標跟蹤的組網雷達功率時間聯合優化算法

時晨光 董 璟 周建江

(南京航空航天大學雷達成像與微波光子技術教育部重點實驗室 南京 210016)

1 引言

當前，空戰逐漸由信息化向智能化過渡，通過多雷達協同能夠提高空天目標的預警探測能力與情報保障能力，特別是能夠提高復雜戰場條件下對非合作特種軍用目標的連續探測跟蹤能力，已成為國內外研究人員的共識。與此同時，隨著軍事裝備技術的飛速發展，多雷達協同的作戰環境也變得越來越復雜，電磁頻譜環境的復雜性、時變性以及難以預測性，對雷達系統提出了嚴峻挑戰。如何讓雷達系統在與通信基站共享同一工作頻段的條件下，通過優化自身的射頻輻射資源配置以提升其探測跟蹤性能，已經成為一個熱點問題[1–7]。

對于共享頻譜的雷達和通信系統，需要設計有效的管理方案來減少兩者間的相互干擾，從而保證彼此都能正常工作[8–18]。針對該問題，Zheng等人[9]提出了一種非合作雷達/通信共存的自適應干擾消除方法，優先考慮保護通信系統性能，并通過求解凸問題對雷達參數和通信解調誤差進行估計，仿真結果驗證了算法的有效性與優越性。魯彥希[10]以雷達對通信系統的干擾能量為約束條件，對組網雷達節點選擇與功率參數進行自適應優化設計。文獻[11]提出了用于多雷達系統中多目標跟蹤的通信感知資源調度策略，考慮在最小化雷達對通信干擾的同時，對雷達發射功率和采樣間隔進行優化分配，仿真結果表明，該算法能夠有效提高系統多目標跟蹤性能。文獻[12]針對異構雷達與通信系統之間的頻譜共存問題，通過分配有限的發射功率、駐留時間和共享帶寬資源，來提高組網雷達的跟蹤性能，同時保持通信下行鏈路的吞吐量水平。文獻[13]對通信系統傳輸協方差矩陣以及基于稀疏感知和矩陣補全的多輸入多輸出(Multi-Input Multi-Output,MIMO)雷達采樣方案進行聯合設計，旨在保持通信系統的平均容量和發射功率的同時，最大限度地降低雷達接收機處的有效干擾功率。Hessar等人[14]采用具有低復雜度的空頻域隔離機制，并結合具體的雷達通信系統操作策略解決頻譜共存問題。韓凱峰等人[15]提出了一種雷達通信頻譜共存場景下基于塊對角化的通信雷達波束設計方案，該方案以通信對雷達無干擾及通信用戶間無干擾為約束，在滿足功率資源約束的條件下，最大化通信系統和速率。仿真結果表明，所提算法適用于多種場景，且與現有算法相比，具有更低的計算復雜度和更好的通信性能。文獻[16]針對多雷達通信一體化系統相互干擾的問題，提出了基于正交頻分復用(Orthogonal Frequency Division Multiplexing,OFDM)子載波分配的雷達通信一體化系統，利用子載波間的互相正交性，消除雷達與通信用戶間干擾以及通信用戶之間的相互干擾。文獻[17]提出了頻譜共存下基于Stackelberg博弈的多基地分布式雷達功率分配算法，在滿足預先設定的目標探測信干噪比閾值的情況下，最小化各雷達輻射功率，從而起到保護通信基站不受雷達射頻輻射干擾。

組網雷達具有多雷達探測資源協同運用與信息融合緊密結合的技術體制特點，且在目標檢測、跟蹤、識別等諸多場景中均具有顯著優勢[19]。射頻資源管理是組網雷達目標跟蹤任務中重要的一環，通過對輻射功率、駐留時間、信號帶寬和輻射采樣間隔等射頻參數進行優化，能夠有效提升雷達系統性能[20–35]。Zhang等人[20]對雜波環境下分布式MIMO雷達多目標跟蹤的資源分配問題進行了研究，通過對雷達節點和功率資源進行自適應優化配置，最小化多目標跟蹤誤差，并提出了次優解排序方法對該優化模型進行求解。Lu等人[21]提出了一種機載雷達路徑規劃與輻射資源聯合優化算法，該算法將機載雷達路徑規劃和輻射資源作為優化參數，并采用多目標跟蹤誤差效用函數作為優化目標，采用多步分解法和梯度投影法對該問題進行求解，仿真結果表明，該算法有效提升了雷達系統多目標跟蹤性能。文獻[22]提出了面向低截獲概率的機載雷達功率資源分配算法，該算法以包含雷達多目標跟蹤誤差和截獲概率的加權為目標函數，并采用兩步分解法對模型進行求解。仿真結果表明，該算法能夠有效降低跟蹤過程中雷達被敵方無源探測系統截獲的概率。文獻[23]提出了一種多目標跟蹤場景下的相控陣雷達最優資源分配算法，該算法以多目標跟蹤性能作為約束條件，以最小化雷達資源消耗為優化目標，對雷達的功率和帶寬參數進行聯合優化分配。Cheng等人[24]提出了同時多波束集中式MIMO雷達自適應時空資源與波形聯合優化算法，該算法采用智能優化方法對雷達采樣周期、發射能量、子陣列數和多波束方向矢量等多個參數進行聯合優化設計，能夠自適應選擇工作模式，從而在最大化目標跟蹤精度的同時，達到最小化雷達資源消耗的目的。文獻[25]以最小化雷達駐留時間和輻射功率資源加權和為優化目標，結合內點法和匈牙利算法對雷達節點分配方式、輻射功率和駐留時間進行優化，仿真結果表明，相較于資源均勻分配算法，該算法能夠有效提升雷達系統的射頻隱身性能。文獻[26]對多基地雷達之間的博弈優化模型進行分析，將預先設定的信干噪比閾值作為約束條件，結合凸優化方法和博弈思想，對多基地雷達功率分配和波束形成進行聯合優化，仿真結果驗證了該算法對雷達間的干擾抑制能力。文獻[27]提出了基于Stackelberg博弈的組網雷達功率分配算法，該算法旨在最小化功率消耗的同時最優化目標跟蹤精度，仿真結果表明，該算法能夠有效提高雷達系統的資源利用率。嚴俊坤等人[28]提出了基于機會約束的集中式MIMO雷達功率分配算法，該算法以MIMO雷達高概率滿足多目標跟蹤精度為約束條件，以最小化MIMO雷達的發射功率為優化目標，并采用凸優化方法對優化模型進行求解。文獻[29]提出了分布式MIMO雷達多目標跟蹤接收波束資源分配算法，該算法能夠基于跟蹤周期中的反饋信息，采用內點法實現接收波束與目標之間的最優分配。

綜上所述，上述研究成果為優化組網雷達目標跟蹤性能和解決雷達通信頻譜共存問題奠定了堅實的基礎。然而，針對多目標跟蹤場景，文獻[10,11]等已有研究并未充分考慮雷達通信頻譜共存環境下組網雷達功率時間資源的聯合優化配置，解決該問題對于提升我方雷達探測系統的目標跟蹤精度、射頻資源利用率及對敵作戰效能具有重要意義。因此，本文圍繞多目標跟蹤場景下雷達通信頻譜共存和組網雷達輻射資源管理領域，研究了頻譜共存下面向多目標跟蹤的組網雷達射頻資源聯合優化分配問題。首先，由于各優化參數的約束不同，采用發射能量作為優化參數的算法復雜度較高，因此針對頻譜共存環境下多目標跟蹤問題，建立了組網雷達功率時間資源聯合優化模型，以最小化多目標跟蹤貝葉斯克拉默-拉奧下界(Bayesian Cramér-Rao Lower Bound,BCRLB)為優化目標，以給定的組網雷達射頻資源和預先設定的通信基站最大可容忍干擾能量閾值為約束條件，通過聯合優化雷達節點選擇、發射功率和駐留時間等射頻輻射參數，提升組網雷達的多目標跟蹤精度。仿真結果驗證了本文所提算法的可行性和穩健性。

2 系統模型

考慮一個由N部雷達組成的組網雷達系統，各雷達節點分散部署于二維直角坐標系中，并保持時間、空間、頻率同步。第n部雷達的位置坐標可以表示為xR,n=(xR,n,yR,n),n=1,2,...,N。另外，假設組網雷達系統的探測范圍內存在Q個運動目標和C個通信基站。

2.1 目標運動模型

式中，rq表示過程噪聲強度。

2.2 雷達量測模型

2.3 干擾模型

通信基站在一定頻帶范圍內持續性向外輻射電磁信號，會使雷達系統的探測跟蹤性能下降。另外，在頻譜共存環境下，雷達在執行目標探測跟蹤任務時也會對通信基站的正常工作造成負面影響。因此，本節對雷達和通信基站兩者的相互干擾進行分析。首先，考慮通信基站對雷達的干擾，此類干擾可以看作多種隨機調制信號的組合。根據中心極限定理，假設信號形式可近似表示為占據一定帶寬的循環對稱帶限的復高斯序列，該信號的功率譜密度(Power Spectral Density,PSD)在雷達的工作通帶范圍內表現出了均勻特性[36]，即

式中，Nm,n表示信號PSD強度；fU,m,n和fL,m,n分別表示第m個通信基站和第n部雷達共同覆蓋頻帶的上界和下界。定義第m個通信基站對第n部雷達產生的干擾信號的時域協方差矩陣Ξm,n可以表示為[10]

式中，Ξm,n的第u行第v列的元素為對應信號延時的自相關函數，同時也是通信基站信號PSD的離散時間傅里葉逆變換；Ts表示信號采樣周期。考慮到距離衰減等因素影響，第m個通信基站對第n部雷達施加的干擾噪聲為

式中，χm,n表示傳輸信道的強度系數；表示第m個通信基站在第n部雷達頻帶范圍產生的干擾序列；表示通信基站m相對于雷達n的方位角。假設各通信基站的發射信號相互正交，則所有通信基站對雷達n的干擾時域協方差矩陣可以表示為

式中，xC,m表示第m個通信基站的位置。由式(8)可知，(fU,m,n-fL,m,n)值越大，則通信基站對雷達的干擾能量越強；如果第m個通信基站和第n部雷達在頻譜上沒有覆蓋，則fU,m,n-fL,m,n=0，即可認為對應的干擾強度為0。

雷達在跟蹤運動目標時對通信基站的干擾是時變的，且與目標的運動狀態有關。本文使用雷達發射信號能量的聯合空頻域分布來表征干擾強度，可以計算為

式中，sn=[sn(1),sn(2),...,sn(L)]T表示具有有限間隔的雷達波形序列；表示雷達發射信號能量的空間分布[10]，即

3 頻譜共存下面向多目標跟蹤的組網雷達功率時間聯合優化算法

針對頻譜共存環境下多目標跟蹤資源分配問題，提出一種面向多目標跟蹤的組網雷達功率時間聯合優化分配算法，旨在滿足給定雷達系統射頻資源和預先設定的通信基站最大可容忍干擾能量閾值等約束的條件下，對雷達節點選擇、發射功率和駐留時間等射頻參數進行自適應優化配置，從而在保證通信基站正常工作的同時，有效提升組網雷達的多目標跟蹤精度。

3.1 優化模型建立

在建立優化模型之前，需要推導表征目標跟蹤精度衡量指標的解析表達式。文獻[37]中指出，在參數無偏估計的條件下，BCRLB為運動目標跟蹤的均方誤差提供了下界，可以用來表征組網雷達跟蹤運動目標的性能衡量指標。首先，推導出k時刻目標q的預測貝葉斯信息矩陣表達式為

本文提出了一種頻譜共存下面向多目標跟蹤的組網雷達功率時間聯合優化算法，通過聯合優化分配雷達節點選擇、發射功率和駐留時間等射頻輻射參數，在滿足給定的雷達射頻資源和預先設定的通信基站最大可容忍干擾能量閾值的條件下，最大限度地降低組網雷達系統的多目標跟蹤誤差，可構建如下數學優化模型：

式中，Tmax和Tmin分別表示各雷達駐留時間的上界和下界；Pmax和Pmin分別表示各雷達發射功率的上界和下界；Ttotal和Ptotal分別表示照射各目標的所有雷達駐留時間和發射功率之和；Emax表示通信基站所能容忍的最大雷達干擾能量閾值；表示k時刻每部雷達最多可跟蹤一個目標；?max表示各時刻組網雷達跟蹤目標q可選擇的最多雷達節點數目。

3.2 優化模型求解

同樣地，設定發射功率和駐留時間兩個參數的優先級相同，采用SDP算法對優化模型(19)進行求解，得到所選擇雷達節點的發射功率和駐留時間分配值，進而可以得到(?max-1)個射頻資源配置方案及其對應的多目標跟蹤誤差。

步驟3 選取步驟2所有方案中最小的多目標跟蹤誤差與其對應的射頻資源優化分配方案作為備選方案，并將該資源優化分配結果作為下一次循環的初始值。跳轉至步驟1，直到連續兩次得到的備選方案多目標跟蹤誤差差值小于某一設定的閾值時，跳出循環，并將得到的優化分配方案作為k時刻跟蹤目標q的最優雷達節點選擇方案和功率時間優化分配方案。

步驟4 確定下一個跟蹤的目標，移除步驟3已選取的雷達節點，跳轉至步驟1，直到對所有目標的跟蹤方案都完成優化，即可得到k時刻組網雷達跟蹤多目標時的雷達節點選擇方案和功率時間聯合優化分配方案。上述算法流程如算法1所示。

4 仿真結果及分析

為了驗證頻譜共存下面向多目標跟蹤的組網雷達功率時間聯合優化算法的可行性與有效性，本節進行了如下仿真：假設組網雷達系統由N=6部位置固定且已知的雷達組成，各部雷達的系統參數均相同。組網雷達系統在k時刻需要同時跟蹤Q=2個目標，目標1的初始位置為[-70,0] km，以速度[900,400] m/s勻速飛行；目標2的初始位置為[70,80] km，以速度[-900,-400] m/s勻速飛行。在組網雷達探測區域中存在C=2個通信基站，如圖1所示，兩個通信基站位置分別為[50,50] km和[–40,50] km。雷達采樣間隔為ΔT=3 s，跟蹤持續過程時間為 150 s，共50幀。k時刻跟蹤某一目標的雷達節點數目最大值?max=3，通信基站最大可容忍干擾能量閾值為Emax=4.2J。其中，組網雷達仿真參數設置如表1所示。本文針對RCS不變、RCS變化和Emax閾值變化3種仿真場景分別進行仿真。

表1 仿真參數設置Tab.1 Simulation parameter settings

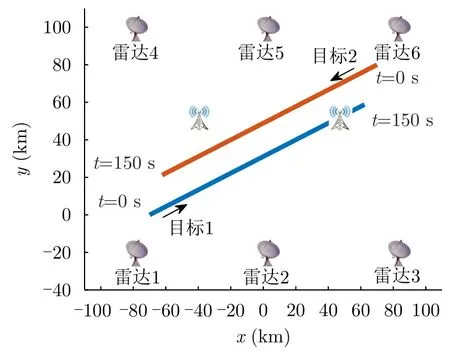
圖1 組網雷達布陣及多目標運動軌跡圖Fig.1 Deployment of radar networks and trajectories of multiple targets

4.1 RCS不變

在該仿真場景中，假設雷達節點觀測運動目標的RCS均為1 m2，組網雷達布陣及多目標運動軌跡如圖1所示。

圖2給出了組網雷達跟蹤目標1和目標2的節點選擇和功率時間資源優化分配結果，黑色部分表示該雷達節點在相應幀未被賦予目標跟蹤任務，即=0；反之，則表示該雷達節點在相應幀被賦予目標跟蹤任務，即=1。從圖2可以看出，組網雷達系統會優先選擇距離目標較近的雷達節點進行跟蹤，且各部雷達的發射功率和駐留時間分配情況均隨著目標運動狀態變化自適應進行調整。例如，前28幀組網雷達系統均選擇了距離目標1更近的雷達1和雷達2進行跟蹤，隨著目標1逐漸遠離雷達1而靠近雷達2，分配給雷達1的射頻資源也在不斷增加；對于目標2，前8幀組網雷達系統選擇了距離目標2更近的雷達5和雷達6進行跟蹤，并向與目標2距離變大的雷達6分配更多的射頻資源。

圖2 雷達節點選擇與功率時間資源優化分配結果Fig.2 Radar node selection and allocation results of power and dwell time resources

同時，組網雷達系統的節點選擇結果也受到通信基站最大可容忍干擾能量閾值的影響。例如，從第40幀開始，目標1與通信基站距離小，雷達對通信基站的干擾能量接近通信基站最大可容忍干擾能量閾值，導致每一幀都會選擇不同的雷達節點對目標1進行跟蹤。同樣地，對于目標2，從第9幀開始，組網雷達系統選擇對通信基站干擾較弱的雷達3替代雷達5對目標2進行跟蹤。

為了進一步驗證本文所提算法的優越性，將所提算法的多目標跟蹤誤差與其他4種對比算法進行比較。

(1) 無通信干擾算法。該算法不考慮通信基站與組網雷達之間的相互干擾，采用本文所提兩步分解求解方法對組網雷達節點選擇、發射功率和駐留時間等射頻輻射參數進行優化配置。

(2) 隨機節點選擇算法。該算法對各時刻跟蹤目標的雷達節點進行隨機選擇，并采用本文所提求解方法對選擇的雷達進行發射功率和駐留時間優化配置。

(3) 均勻時間分配算法。該算法固定各雷達駐留時間，僅優化雷達節點選擇和發射功率分配。

(4) 均勻功率時間分配算法。該算法固定各雷達的發射功率和駐留時間，僅優化雷達節點選擇。

定義k時刻目標跟蹤的平均均方根誤差(Average Root Mean Square Error,ARMSE)為

式中，NMC為蒙特卡羅實驗次數；為第n次蒙特卡羅實驗得到的目標位置估計，本文設定NMC=100。本文所提算法和上述4種算法的ARMSE對比結果如圖3所示。從圖3可以看出，本文所提算法相較于有固定資源分配算法和隨機節點選擇算法具有更低的多目標跟蹤誤差，這說明雷達節點選擇和射頻資源優化分配對提升多目標跟蹤精度有較大影響，而且優化的射頻資源越多，各目標跟蹤精度也越好。由于無通信干擾算法中不存在通信基站，即不考慮雷達與通信基站間的相互干擾，其所得多目標跟蹤誤差低于本文所提算法，這也進一步說明了通信基站的存在對組網雷達多目標跟蹤性能有一定影響。總的來說，本文所提算法能夠在給定組網雷達射頻資源條件和預先設定的通信基站最大可容忍干擾能量閾值下，通過聯合優化雷達節點選擇以及輻射功率與駐留時間等射頻資源配置，獲得相較于其他對比算法更優的多目標跟蹤精度。

圖3 RCS不變場景下ARMSE對比結果Fig.3 Comparison results of ARMSE with same RCS

4.2 RCS變化

在該仿真場景中，主要研究目標RCS的變化對組網雷達射頻資源配置與多目標跟蹤精度的影響。目標1和目標2相對于雷達3和雷達4的RCS模型為Swerling I型，其中，各目標RCS變化情況如圖4所示，目標相對于其他雷達節點的RCS值仍固定為1 m2。

圖4 各目標RCS數值Fig.4 RCS values of each target

圖5給出了RCS變化情況下組網雷達跟蹤目標1和目標2的雷達節點選擇和功率時間資源優化分配結果。從圖5可以看出，由于目標回波信噪比與其RCS值呈正比關系，組網雷達系統傾向于選擇相對目標RCS值較大的雷達節點來完成跟蹤任務。例如，各目標相對于雷達3和雷達4的RCS值在大多數跟蹤時刻均高于其他雷達，相較于RCS不變條件下的節點選擇方案，由于目標1和目標2相對于雷達3和雷達4的RCS值在多數時刻均高于RCS不變場景下的RCS設定值，因此組網雷達選擇雷達3和雷達4來跟蹤目標1和目標2的時刻顯著增多；同時，為了獲得更好的目標跟蹤精度，本文所提算法更多選擇3部雷達對目標進行跟蹤。

圖5 RCS變化場景下雷達節點選擇與功率時間資源優化分配結果Fig.5 Radar node selection and allocation results of power and dwell time resources with various RCS

同樣地，RCS變化情況下本文所提算法與其他對比算法的ARMSE對比結果如圖6所示。由于雷達節點選擇受到目標RCS變化的影響，組網雷達的跟蹤性能略差于RCS不變情況下的跟蹤性能，但仍優于同一場景下的其他對比算法，體現了本文所提算法的穩健性。

圖6 RCS變化場景下ARMSE對比結果Fig.6 Comparison results of ARMSE with various RCS

4.3 Emax變化

在該仿真場景中，主要研究通信基站最大可容忍干擾能量閾值，即Emax變化對組網雷達多目標跟蹤精度的影響。圖7給出了Emax=3 J時組網雷達跟蹤目標1和目標2的節點選擇和功率時間資源優化分配結果。從圖7可以看出，相較于第1種仿真場景，由于Emax值變小，通信基站對雷達干擾能量的可容忍度降低，此時，組網雷達選擇了滿足約束條件下的最優雷達射頻資源分配方案；類似地，組網雷達更多地選擇3部雷達對多目標進行跟蹤。

圖7 Emax=3 J時雷達節點選擇與功率時間資源優化分配結果Fig.7 Radar node selection and allocation results of power and dwell time resources with Emax=3 J

同樣地，圖8顯示不同Emax條件下本文所提算法與其他4種算法的ARMSE對比結果。從圖中可以看出，隨著Emax值不斷增加，通信基站對雷達干擾能量的可容忍度不斷提升，使得可供組網雷達配置的射頻輻射資源增多，于是，系統能夠得到更低的多目標跟蹤誤差，所得ARMSE值也更逼近無通信干擾條件下的跟蹤誤差。

圖8 不同Emax條件下ARMSE對比結果Fig.8 Comparison results of ARMSE under different Emax conditions

5 結語

本文考慮了頻譜共存環境下通信基站對組網雷達多目標跟蹤性能的影響，提出了一種面向多目標跟蹤的組網雷達功率時間聯合優化算法，以滿足組網雷達射頻資源和預先設定的通信基站最大可容忍干擾能量閾值為約束條件，以最小化多目標跟蹤BCRLB為優化目標，通過聯合優化分配雷達節點選擇、發射功率和駐留時間等參數，提高了組網雷達的多目標跟蹤精度。仿真結果表明，多目標跟蹤精度不僅與組網雷達和各目標的空間位置關系及目標散射特性有關，而且還受通信基站最大可容忍干擾能量閾值的影響；另外，與現有算法相比，本文所提算法能夠在保證通信基站正常工作的條件下，有效提升多目標跟蹤性能。下一步將圍繞頻譜共存環境下組網雷達射頻輻射參數與飛行路徑聯合優化問題進行研究。