基于小波能量比的同桿雙回輸電線路故障識別

楊 亮 吳 浩* 陳佳豪 顧小平 楊 杰 劉益岑

1(四川輕化工大學自動化與信息工程學院 四川 自貢 643000) 2(國網四川電力公司電力科學研究院 四川 成都 610000)

0 引 言

同桿雙回線路在超(特)高壓等級的輸電線路中應用得越來越廣泛。然而,同桿雙回線路的故障條件變得更加復雜,故障后的危害也更加嚴重,必須在故障后迅速切除故障線路。

眾多學者對同桿雙回線路進行了大量的研究[1-8]。張子衿等[9]對同桿雙回線路在特定條件下保護誤動的情況進行了分析,提出了改變零序反時限保護時間整定系數的方法來避免保護誤動;并對保護兩端的靈敏度配合和改變時間整定系數后帶來的時延問題提出了基于零序電流變化和零序功率方向的加速方案,但算法復雜,不易實現。李世龍等[10]對于同桿并架電流橫差保護在線路參數不平衡時存在的靈敏度低、相繼動作區較大等不足,提出利用同相差/和阻抗比值構造橫差保護,但存在出口死區問題,需要加入補充保護。司泰龍等[11]利用六序分量解耦后的反序負序分量特征,結合縱聯電氣量和縱聯邏輯信號兩種保護原理,提出了基于反序負序縱聯距離保護新方法,但對于單回線對稱故障和同名相跨線故障情況,還存在保護缺陷。綜上可知,由于同桿雙回線路的復雜性,現有的保護原理需要進一步完善。

本文借鑒王永進等[12]的研究方法,分析了同桿雙回線路發生區內/外故障后一段時窗內的反行波電流幅值關系,提出一種基于小波能量比的故障識別方法。本文方法將故障后一段時窗內兩端的反行波電流進行小波分解,提取兩端各尺度下的小波能量比作為特征向量,使用SMOTE算法對少數類樣本進行擴充后,訓練支持向量機分類器,對區內外故障進行識別。實驗結果表明,本文方法能有效保護線路全長,在高阻故障和各種故障類型的情況下都能快速、可靠地進行故障識別。

1 故障行波傳輸特性分析

圖1所示為文中所用的同桿雙回線路模型,其中:M和N為兩端母線;MN定義為保護區內,線路用L1和L2表示,分別代表Ⅰ回線和Ⅱ回線;PM和NO定義為保護區外,線路用L3和L4表示;R1-R6為區內/外靠近M或N端母線的行波保護單元。規定行波由母線流向線路的方向為正方向。

圖1 同桿雙回線路簡化模型

當線路發生故障時,可以等效為正常運行狀態和故障附加狀態的疊加[13]。故障分量狀態相當于在故障點附加一個電源,并且在故障點處產生向線路兩端傳輸的故障行波。

1.1 區內故障行波特性

以單相線路為例,當K1處發生區內故障時,故障行波傳輸過程如圖2所示。

圖2 區內故障時行波傳輸過程

圖2中,τM和τN分別為行波從故障點傳輸至M、N端母線所需時間;τ為行波從母線M傳輸到母線N所用時間;iMf和iMb為M端母線檢測到的前行波電流和反行波電流;iNf和iNb為N端母線檢測到的前行波電流和反行波電流。由圖2分析可知,區內故障時,兩端行波保護單元首先檢測到的故障反行波電流iMb和iNb。若線路一端首先檢測到反行波電流的時間為t,則[t,t+τ]內另一端必定能檢測到反行波電流。

1.2 區外故障行波特性

同樣,當K2處發生區外故障時,故障行波傳輸過程如圖3所示。故障后,N端行波保護單元首先檢測到故障前行波電流iNf,由于線路無斷點,iNf沿線路一直傳輸至M端,變為M端的反行波電流iMb,iMb在M端物理邊界發生反射,得到M端的前行波電流iMf,iMf沿線路傳輸至N端,就成為N端的反行波電流iNb[12]。

圖3 區外故障時行波傳輸過程

分析圖3可知,若故障發生后N端檢測到故障前行波iNf時間為t,則在[t,t+2τ)內,N端理論上檢測不到反行波iNb,而M端可以檢測到反行波iMb。

1.3 反行波電流特征總結

基于以上分析可知,區內故障時,在故障后[t,t+2τ)內,線路兩端行波保護單元都可以檢測到反行波,且兩端的幅值差異較小;區外故障時,在故障后[t,t+2τ)內,線路一端的行波保護單元可以檢測到反行波,但另一端理論上檢測不到反行波,反行波幅值差異較大,可以比較線路兩端的能量差異實現區內/外故障識別。

M、N端的電流反行波計算公式為:

(1)

式中:Zc為線路波阻抗;uM、uN、iM、iN分別為兩端電壓、電流。

2 算法實現

利用相模變換對同桿雙回線路兩端的行波電壓、電流進行解耦,選取同一模量計算兩端反行波模量電流,使用小波分解將模量電流分解到6個尺度的頻帶上,計算每個尺度故障后[τ,2τ)內的小波能量,提取兩端各尺度下的小波能量比特征構成訓練樣本,經SMOTE算法擴充少數類樣本后,訓練支持向量機分類器,對區內外故障進行識別。

2.1 相模變換

在同桿雙回線路中,為避免線路耦合的影響,需要利用相模變換矩陣將耦合線路解耦成相互獨立的單相系統[14]。本文采用王守鵬等[15]提出的相模變換方法,其變換矩陣如式(2)所示。

(2)

變換關系如式(3)所示。

(3)

式中:uT0、uT1、uT2、uF0、uF1、uF2分別為單端的同向和反向0模、1模和2模量電壓。

2.2 小波分解

小波分解就是將待分解信號進行雙通道濾波的過程。信號的小波分解過程如圖4所示,首先將信號X進行第1層高通、低通濾波,得到第1次分解的低頻概貌A1和高頻細節D1;保存D1為最終信息。A1再次分解得到第2次分解的低頻概貌A2和高頻細節D2,保存D1為最終信息。重復以上操作n次,最終得到D1,D2,…,Dn和An[16]。

圖4 小波分解過程

對采樣頻率為fs的信號進行小波分解,每層輸出的采樣率都在上層頻率的基礎上減半,則第n層信號所在頻帶為[fs/2n+1,fs/2n]。

2.3 區內外故障反行波電流分析

2.3.1 區內單回線故障反行波電流分析

保護區內L2線路A、B相發生短路接地故障后[τ,2τ)內的兩端反行波電流相關波形如圖5、圖6和圖7所示。從圖5可以看出,在[τ,2τ)內兩端都能夠檢測到反行波信號;比較圖6和圖7可知,反行波電流分解后,M端和N端的對應尺度上的電流大小相差不大,能量相差不大。

圖5 區內單回線故障兩端電流波形

圖6 區內單回線故障M端小波分解波形

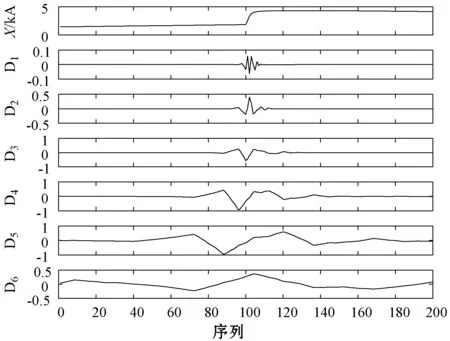
圖7 區內單回線故障N端小波分解波形

2.3.2 區內同名相跨線故障反行波電流分析

保護區內L1線路A相和L2線路A相發生同名相短路接地故障后[τ,2τ)內的兩端反行波電流相關波形如圖8、圖9和圖10所示。從圖8可以看出,在[τ,2τ)內兩端都能夠檢測到反行波信號;比較圖9和圖10可知,反行波電流分解后,M端和N端的對應尺度上的電流大小相差不大,能量相差不大。

圖8 區內同名相跨線故障兩端電流波形

圖9 區內同名相跨線故障M端小波分解波形

2.3.3 區外故障反行波電流分析

保護區外A、B相發生短路接地故障后[τ,2τ)內兩端的反行波電流相關波形如圖11、圖12和圖13所示。從圖11可以看出,在[τ,2τ)內一端母線能夠檢測到反行波信號,但另一端母線不能明顯檢測到反行波信號;比較圖12和圖13可知,反行波電流分解后,M端和N端的對應尺度上的電流大小相差較大,能量相差很大。

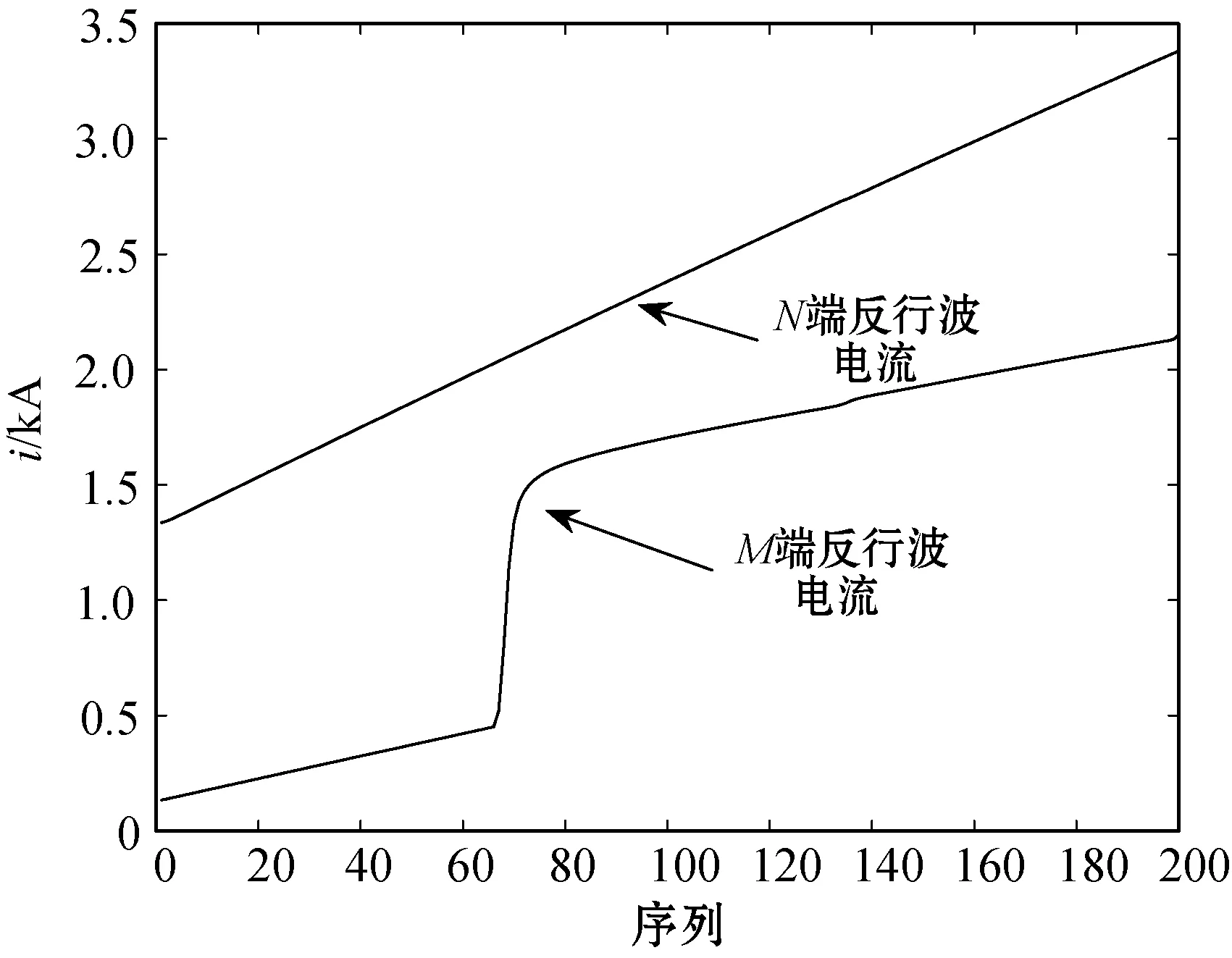
圖11 區外故障兩端電流波形

圖12 區外故障M端小波分解波形

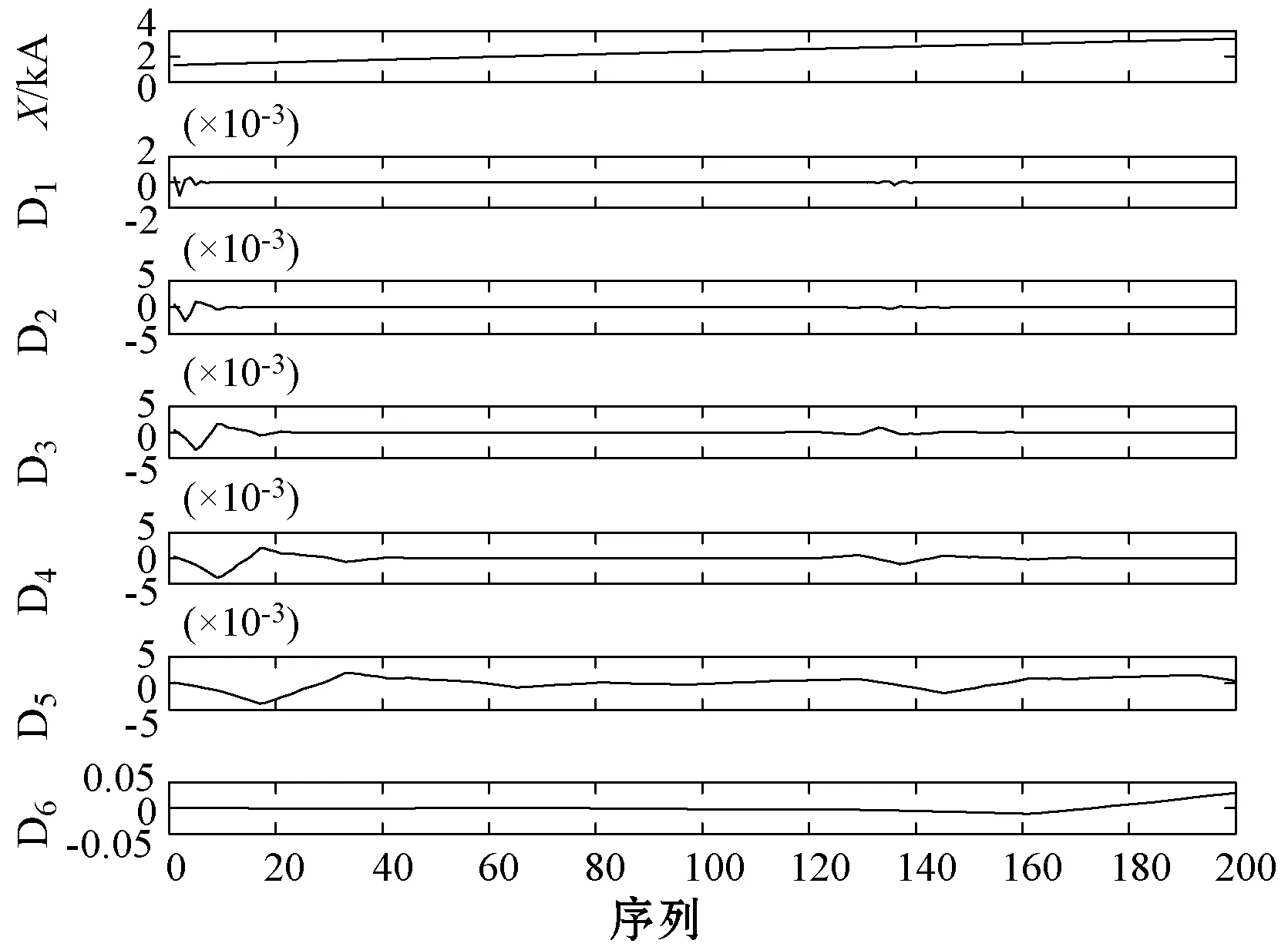
圖13 區外故障N端小波分解波形

仿真發現:區內故障時,兩端各尺度的能量相差不大;區外故障時,兩端各尺度的能量差異較大。驗證了理論分析的正確性,可以將兩端的小波能量比作為特征向量進行故障識別。

2.4 小波能量比故障特征提取

經小波分解可以得到分布在不同頻帶上的故障信號,且沒有頻帶重疊。各頻帶信號的能量包含豐富的故障信息,可用于故障識別。

定義某一尺度的小波能量為該尺度小波變換系數平方沿時間軸的積分[17]。表達式如下:

(4)

式中:EMn、ENn分別為M、N端第n層的小波能量;EMn(t)、ENn(t)為M、N端第n層的小波變換系數;t0為故障發生時間;τ為行波從母線一端傳輸到另一端的時間;本文線路全長為300 km,τ的取值為1 ms。

小波能量比計算式為:

(5)

Pn為第n層的反行波電流能量比。則能量比序列為:

P=[P1,P2,…,Pn,…]

(6)

將反行波模量電流進行6層分解,得到6個尺度的小波能量,最后將6個尺度的小波能量比特征向量[P1,P2,P3,P4,P5,P6]輸入支持向量機進行故障識別。

3 基于支持向量機的故障識別算法

3.1 SMOTE算法

SMOTE算法是樣本不均衡時的處理方法。其思路是在鄰近的少數類樣本間用隨機線性插值的方式來增加少數樣本的數量,使得樣本平衡。

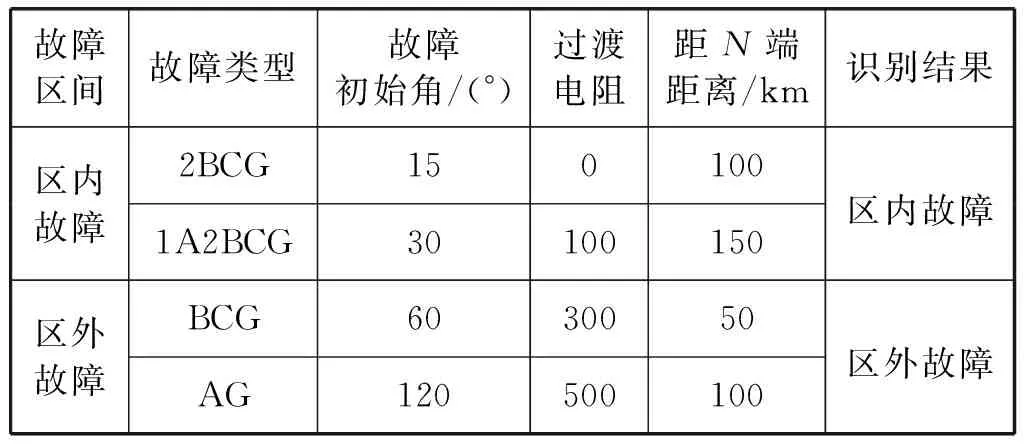
設pi=(xi1,xi2,…,xin)T為樣本集中少數類樣本,n為樣本屬性個數,使用k近鄰法確定pi的k個鄰近樣本,若鄰近樣本中含多數類樣本,則放棄該樣本插值[18]。從k個鄰近樣本中選取l個(l

(7)

3.2 支持向量機

支持向量機[19](Support Vector Machine,SVM)是建立在機器學習理論基礎上的網絡模型;其目的是通過映射函數把樣本映射到高維度的空間內,將非線性問題轉化為線性可分問題,實現對輸入樣本的分類。

選擇非線性變換φ(x)映射到高維空間內[20]。則SVM的目標優化為:

(8)

s.t.yi[ωTω(xi)+b]≥1-ξi

ξi≥0

i=1,2,…,n

式中:ω為方向向量;xi為輸入特征;yi為輸出目標;C是懲罰因子;ξi是松弛變量;b是偏置項[21]。

引入αi構造拉格朗日函數方程,得到目標函數:

(9)

當ω、b、ξ極小值且αi最大值時,對式(9)求偏導并拉格朗日對偶化得到決策函數:

(10)

0≤αi≤C,i=1,2,…,n

將核函數K(x,x′)=φT(x)φ(x′)代入式(10)可得到SVM的最優分類函數:

(11)

本文采用高斯核函數進行分類,它能最大化樣本間距[22],其表達式如下:

(12)

式中:σ為核函數的寬度系數。

3.3 算法流程

同桿雙回線路故障時,通過相模變換對兩端的行波電壓、電流進行解耦;選取同一模量計算兩端反行波電流;選取故障后[τ,2τ)內的反行波模量電流進行6層小波分解,再計算各尺度的小波能量,最后按照式計算兩端對應尺度的小波能量比;提取6個小波能量比[P1,P2,P3,P4,P5,P6]作為特征向量,使用SMOTE算法擴充少數類樣本后,訓練SVM分類器,實現區內外故障的識別。故障識別流程如圖14所示。

圖14 故障識別流程

4 仿真驗證

采用PSCAD軟件建立同桿雙回線路模型,模型如圖1所示。保護區內線路MN長300 km,保護區外線路NO長150 km。系統采樣為200 kHz;電壓等級為500 kV,頻率為50 Hz。

4.1 訓練樣本的構成

在不同故障類型和故障初始角情況下采集故障樣本,由于同桿雙回線路的復雜性,導致區外故障樣本遠少于區內故障樣本,使用SMOTE算法對區外樣本進行擴充,最后將擴充后的區外故障樣本和區內故障樣本組成訓練集樣本訓練SVM分類器。

4.2 訓練集預測結果

將擴充后的訓練樣本輸入SVM網絡進行訓練,得到一個SVM模型。該SVM模型對于訓練樣本的識別結果如圖15所示,能夠準確地識別區內/外故障。

圖15 訓練集預測結果

4.3 算法測試

將不同故障類型時采集8組區內故障測試樣本和10組區外故障測試樣本輸入SVN模型進行測試,測試的結果如圖16所示。

圖16 不同故障類型下的預測結果

表1、表2和表3分別為SVM模型在不同故障類型、過渡電阻和故障初始角情況下的預測結果,對應的故障條件分別在表中展示。為便于對不同類型的故障進行說明,用1、2分別表示L1、L2線路,用G表接地故障。以1A2BCG為例,它表明L1線路的A相與L2線路的B、C相產生了跨線短路接地故障。

表1 不同故障類型下的預測結果

表2 不同過渡電阻下的預測結果

表3 不同故障初始角下的預測結果

分析表1、表2和表3可知,本文算法在不同故障類型、過渡電阻和故障初始角情況下都能夠準確地識別區內/外故障。由此可得:本文算法不受故障類型、過渡電阻和故障初始角的影響。

4.4 算法性能分析

4.4.1抗CT飽和

為驗證算法的抗CT飽和能力,對于區內/外故障進行了CT飽和實驗;以M端CT飽和為例,采集區內/外故障的樣本輸入SVM模型進行測試,得到的測試結果如表4所示。可以看出,在CT飽和的情況下,本文算法依然能準確識別區內外故障。

表4 抗CT飽和測試

4.4.2 抗噪聲干擾

采集故障后的電壓、電流數據,加入噪聲信號,在信噪比SNR為40、50、60、70 dB的情況下提取能量比特征,輸入到SVM模型中進行測試,測試效果如表5所示。

表5 噪聲干擾測試

可以看出,在信噪比SNR為40 dB的條件下,本文方法也能夠有效識別區/內外故障,抗噪聲性能較強。

4.4.3 故障位置的影響

由于行波能量的衰減與故障點的位置有關,為了探究故障位置對本文方法的影響,以區內B相同名相短路接地故障為例,分別模擬線路上不同位置故障時的數據進行故障識別,測試的結果如表6所示,可以看出本文方法不受故障位置的影響,能夠有效保護線路全長。

表6 故障位置測試

5 結 語

本文分析了區內外故障后一段時窗內反行波電流變化特性,提出一種基于小波能量比的同桿雙回線路故障識別方法。通過理論分析和實驗仿真得到如下結論:

(1) 區內故障時,時窗內兩端行波保護單元都能檢測到反行波信號,且兩端的反行波幅值接近,其能量比值小;區外故障時,時窗內有一端行波保護單元無法檢測到反行波信號,兩端的反行波幅值差異較大,能量比值大。

(2) 本文所提的基于小波能量比的同桿雙回線路故障識別方法能有效保護線路全長,不受故障類型、過渡電阻、故障初始角的影響,并且在噪聲干擾和CT飽和的情況下也能進行故障識別,保護的靈敏性和可靠性較高。