基于LMD和DE-PNN的高壓斷路器機械故障識別方法
陳佳豪 吳 浩,2* 胡瀟濤 顧小平 宋 弘,2
1(四川輕化工大學自動化與信息工程學院 四川 自貢 643000) 2(人工智能四川省重點實驗室 四川 自貢 643000)
0 引 言
高壓斷路器是與日俱增的電力生產生活活動的重要保障,斷路器運行的穩定需要密切關注,而據調查分析表明,發現高壓斷路器故障當中主要是以機械故障(包括操動機構和控制回路)為主[1]。及時地診斷故障類型能有效避免事故的擴大化,于是需要對故障診斷方法進行研究。
高壓斷路器機械故障診斷方法主要基于振動信號進行故障診斷[2-3]。聲音信號與振動信號屬于同源信號,由于傳播介質的不同,聲音信號在采集過程中很大程度上會受到外界噪聲干擾。而且基于聲音信號進行故障診斷的診斷機理并未形成統一的研究標準,所以研究存在一定的局限性[4]。
現階段基于聲音信號進行斷路器故障診斷研究較少,文獻[4]通過篩選和標記正常信號與故障信號的聲音信號幅值分布差異性來實現故障診斷。文獻[5]針對斷路器診斷中聲音信號與外界噪聲難以分離的難題,通過信號的分解重構,利用快速獨立主成分分析法實現對有效信號的分離。近年來也出現一些以振聲信號聯合分析對斷路器故障進行診斷的研究。文獻[6]分別將振動信號和聲音信號進行小波包分解提取能量熵特征,將特征輸入Libsvm進行可信度分配,最后利用D-S證據融合理論進行故障診斷。文獻[7]提出利用聲振信號的特征熵矩陣偏差來診斷故障。文獻[8]通過對振聲信號的去噪以及分解,提取多個特征,利用多特征融合的方式提升特征識別的效果,相較于單一特征能有效提升故障診斷的穩定性以及準確性。
局域均值分解(Local Mean Decomposition,LMD)是Smith提出的一種自適應信號分解方法,可將非平穩信號自適應地分解為若干單分量純調幅-調頻信號之和,在信號處理中應用廣泛[9-10]。LMD與EMD方法相比,具有迭代次數少、端點效應抑制效果好等優點[11-12]。
概率神經網絡(Probabilistic Neural Network,PNN)是于1989年由Specht提出,因為其訓練時間短、擴充性能好、收斂速度快、分類能力強的性能特點在故障診斷領域得到了廣泛的應用[13-14]。但需要對參數進行經驗選取,差分進化算法(Differential Evolution,DE)是一種高效的全局優化算法,具有收斂快、控制參數少且設置簡單等優點[15],利用差分進化優化算法對PNN參數進行優化,能有效地提高故障診斷效果[16]。
本文提出一種基于LMD分解和DE優化概率神經網絡的斷路器機械故障診斷方法。對聲音信號進行LMD分解,選取PF分量與原信號的相關系數進行信號重構,計算重構信號的分段能量熵作為故障的特征向量,將特征向量集輸入DE優化的PNN故障診斷模型進行故障診斷,對斷路器機械故障具有較好的診斷效果,實驗結果表明,相較于傳統PNN算法,本文提出的基于差分進化優化的概率神經網絡算法具有更好的診斷效果,對能量熵的分段處理也能有效提升故障特征提取效果。
1 特征選取
1.1 LMD分解
LMD方法的實質是將復雜的非平穩信號由高頻到低頻自適應分解成多個純調頻信號和包絡信號的乘積,即PF分量和一個單調函數,對于信號具有更好的自適應性。其分解過程如下:
(1) 找出待分解信號x(t)的所有極值點pi,并對任意兩相鄰極值點pi和pi+1取平均值,第i段的平均值即局域均值可以表示為:
(1)
第i段的包絡估計值可以表示為:
(2)
用滑動平均法求取對應的局域均值函數m11以及包絡估計函數a11(t)。
(2) 從信號x(t)中剔除m11(t),得到信號h11(t):
h11(t)=x(t)-m11(t)
(3)
(3) 對h11(t)解調,得到解調信號s11(t):
(4)
重復步驟(1)和步驟(2),對獲得的解調信號s11(t)求局部包絡函數a12(t)。如果a12(t)等于1,則說明解調信號a11(t)是一個純調頻信號,信號分解完畢;如果a12(t)不等于1,則把s11(t)作為待分解數據重復步驟(1)和步驟(2)q次,直到獲得一個純調頻信號s1q(t)時,迭代終止,此時包絡估計函數a1(q+1)(t)等于1。
公式說明如下:
(5)
迭代終止條件為:
(6)
1.2 分段能量熵
LMD分解后的PF分量并不是每個分量都存在利用價值,部分分量可能只包含背景噪聲以及無用的特征信息,與需求的信號特征不同,需要進行篩選。
皮爾遜相關系數是統計學概念,用來描述隨機變量之間的線性相關性,在一般的相關系數準則當中相關系數在0.00~±0.30表示兩列數據微相關,±0.30~±0.50表示實相關,±0.50~±0.80表示顯著相關,±0.80~±1.00表示高度相關。
表1表示每一種狀態的部分特征向量集。其中:CD表示傳動機構卡澀;SD表示基座螺絲松動;TH表示合閘彈簧儲能不足;ZC表示正常狀態。
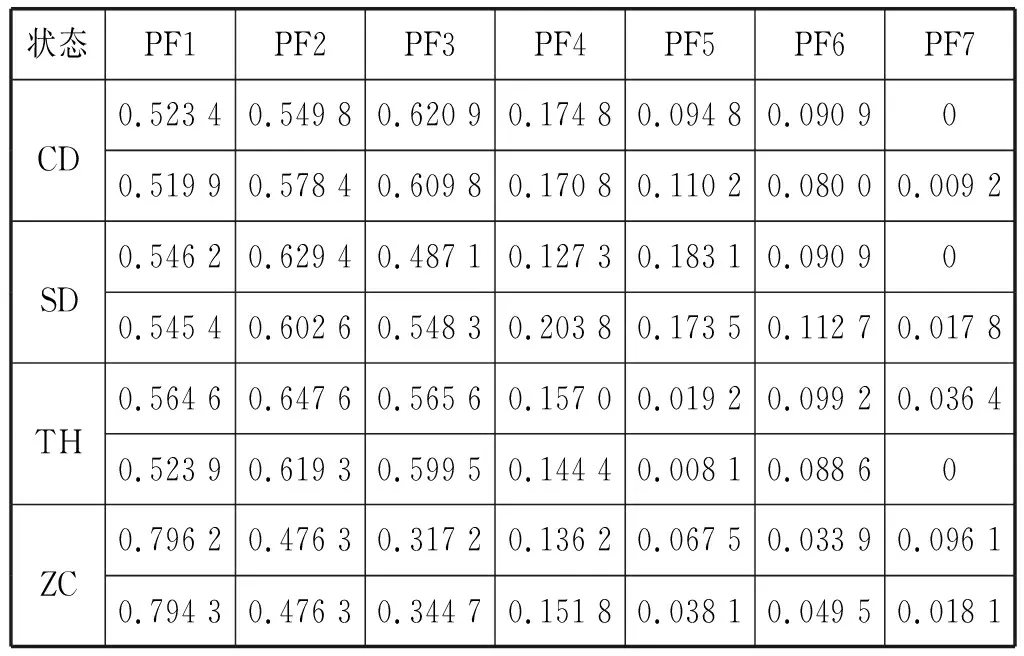
表1 LMD分解7個分量與原始信號的相關系數
依據表1中各分量與原始信號的相關系數值,選取相關系數大于0.3的前3個IMF分量來重構信號。
以傳動機構卡澀為例,圖1是傳動機構卡澀故障的重構前后波形,可以看出經過重構,能有效地剔除一部分干擾,保留更多的有用信息。
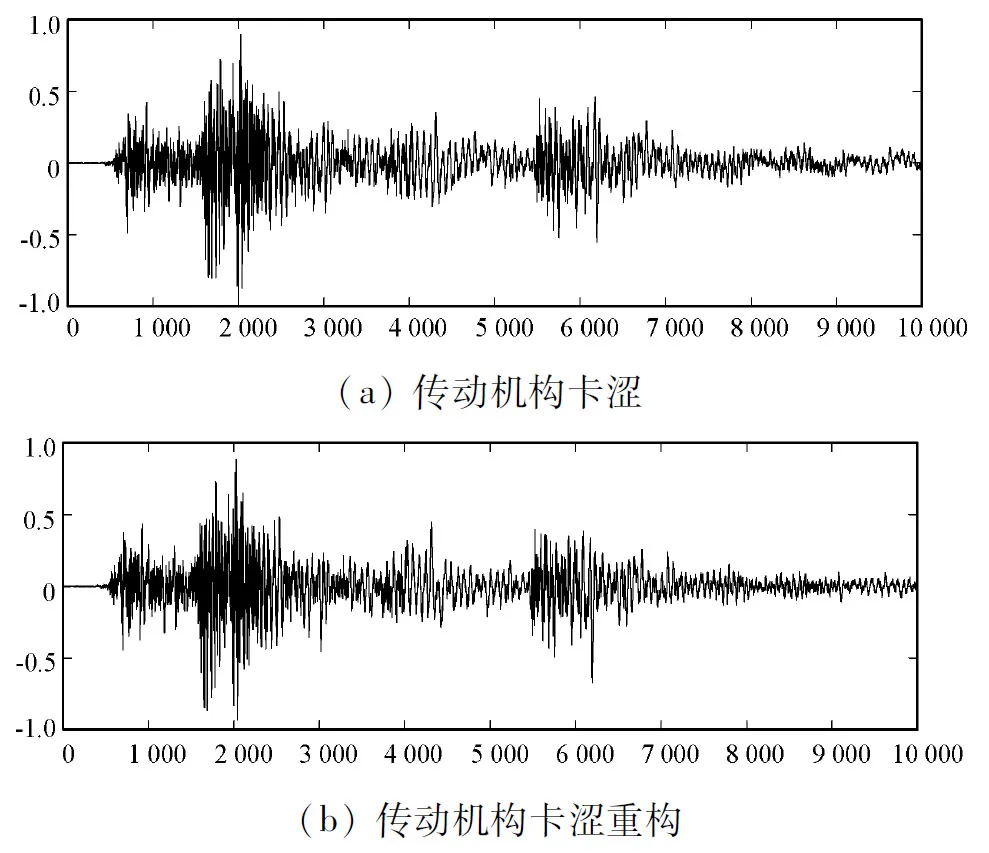
圖1 傳動機構卡澀故障的重構前后波形
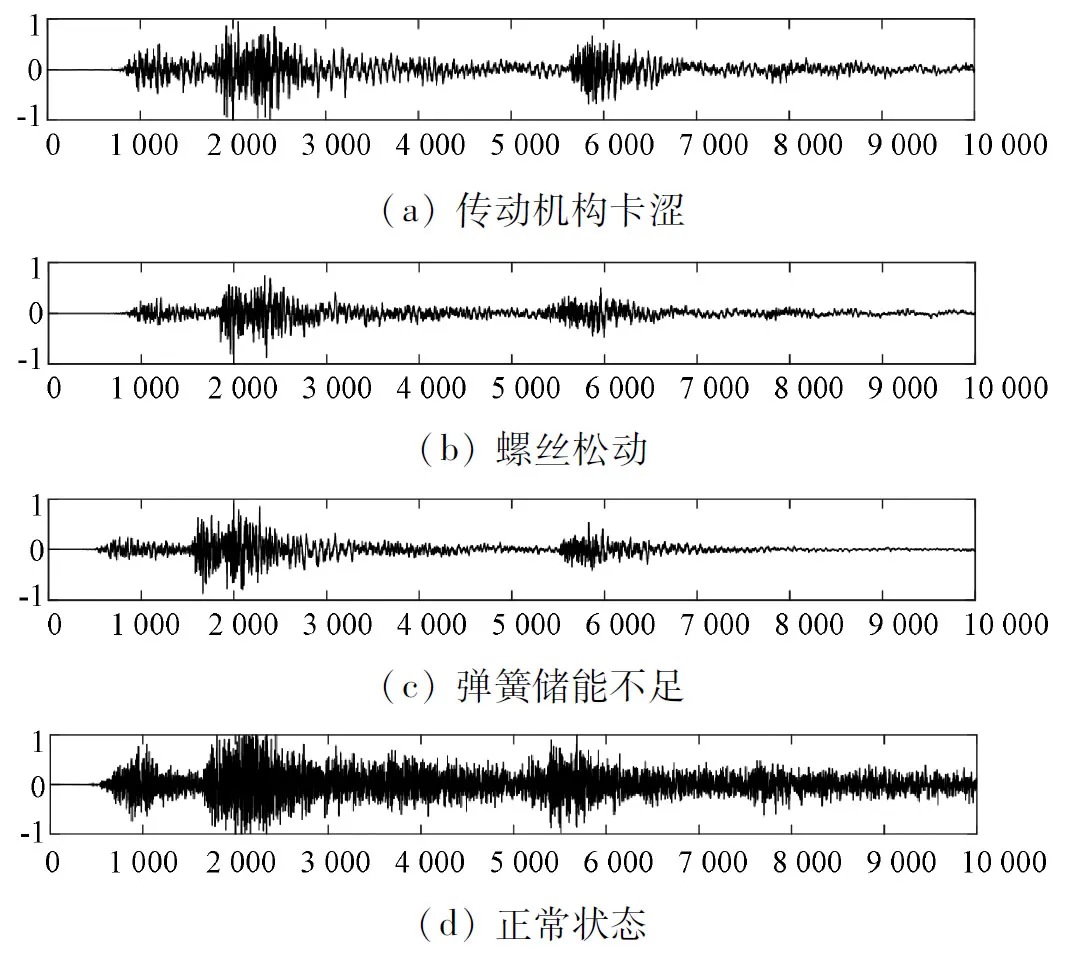
能量熵作為描述序列未知程度的一種信息度量,對于不同類型的序列能有一個直觀化的區別。圖2為四種狀態信號的重構信號。
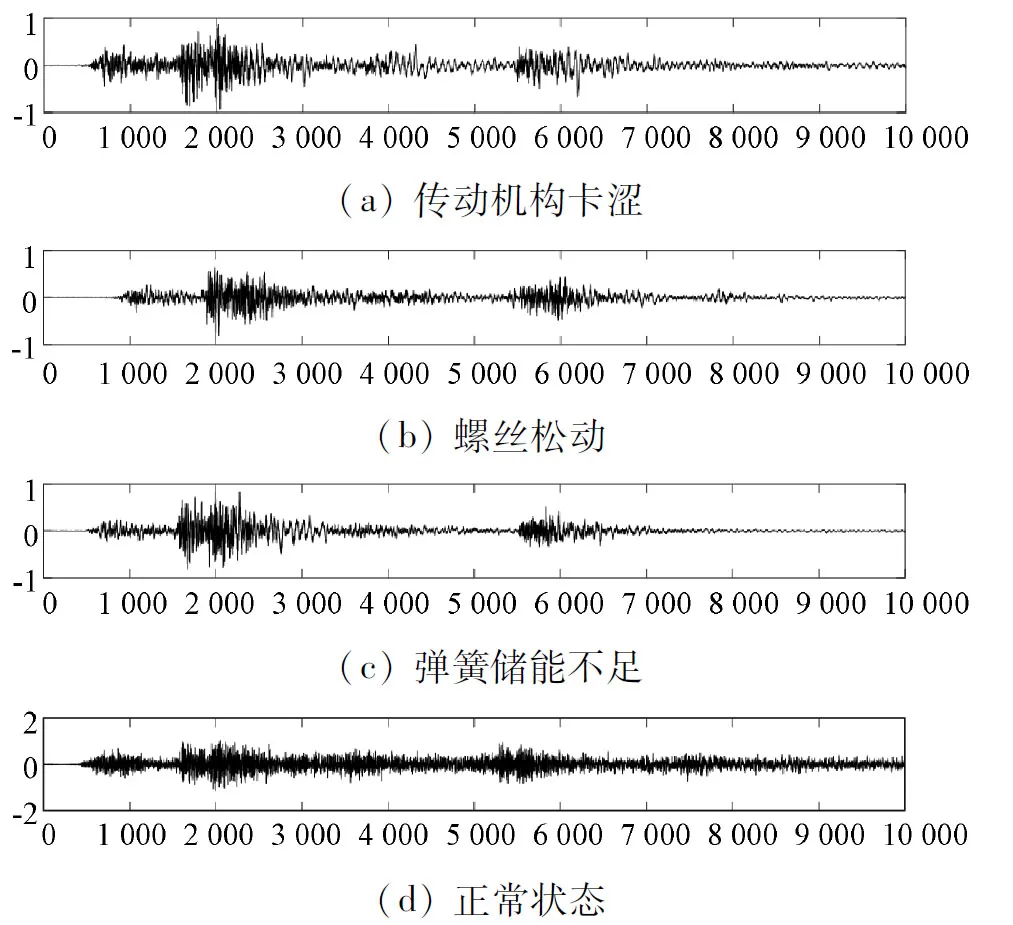
圖2 四種狀態信號的重構信號
可以看出,四種狀態之間的數據序列能量分布差異較為明顯,可以依據不同序列長度的能量差異性實現故障分類。本文將重構信號以每500個采樣點長度截取一次的方式將信號截取成20段,并分別求取每一段的能量熵分布作為特征量。
由能量熵定義公式計算各個分段的能量熵:
(7)
式中:q(i)表示信號i的發生概率。
2 差分進化算法優化概率神經網絡(DE-PNN)
2.1 差分進化算法
差分進化優化算法(DE)是一種非線性全局優化算法,其基本操作主要由種群初始化、變異、交叉和選擇組成。本文選取DE/rand/1/bin差分進化策略進行模型搭建[17-18]。
具體步驟如下:
(1) 初始化種群。在目標搜索空間中隨機均勻地產生m個個體,每個個體是一個n維的向量:
Xi,0=(xi1,0,xi2,0,…,xin,0)
(8)
式中:i=1,2,…,N,N為向量數量;群體種群規模取值5n~10n,n為優化參數數量。
(2) 變異。在第G次迭代中,從種群中隨機抽取3個個體Xc1,G,Xc2,G,Xc3,G,其中c1≠c2≠c3≠i,則第G代參數向量的子代擾動向量:
Si,G=Xc1,G+F·(Xc2,G-Xc3,G)
(9)
式中:F為加權系數,采用自適應變異算法進行更新,增加算法搜索性能。
F=F0·2λ
(10)
其中:
(11)
式中:Gm表示設定的最大迭代次數。
(3) 交叉。經過交叉后的第G+1代的實驗向量Ui,G+1=(u1,i,G+1,u2,i,G+1,…,un,i,G+1),其中每個分量取值如下:
(12)
式中:cri為交叉概率,且cri∈[0,1]。
(4) 選擇。比較實驗向量和預定向量的目標函數值,如果實驗向量具有更優的目標函數值,就用實驗向量代替預定向量;否則,保留預定向量。其更新公式為:
(13)
本文采用測試樣本在概率神經網絡中診斷結果的均方誤差作為DE算法的適應度函數。
2.2 概率神經網絡(PNN)
概率神經網絡是Specht提出的一種前饋型神經網絡。因為其結構簡單、分類效果好、不存在局部最優值問題等優點,如今已廣泛應用于故障診斷領域。
概率神經網絡結構如圖3所示。
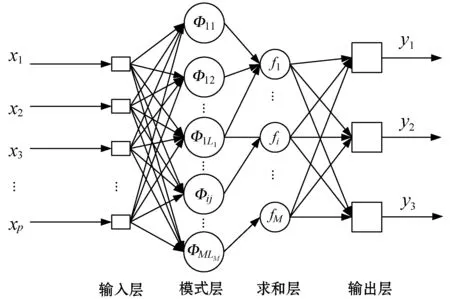
圖3 概率神經網絡的基本結構
(1) 模式層的神經元個數與訓練樣本總數相等,輸入層將輸入的特征向量X與加權系數Wi相乘的標量積Zi傳遞至模式層。選擇exp[(Zi-1)/σ2]作為激活函數,則模式層中第i類的第j個神經元輸出的概率:
(14)
式中:p為訓練樣本的維度;σ為平滑因子;Xij為中心向量。
(2) 求和層的神經元個數與故障類別數相同,第i類類別的概率密度函數fi由模式層中屬于同類別的隱含神經元的輸出加權平均,由Parzen窗方法計算得出:
(15)
式中:Li為類別i的訓練樣本數。
(3) 輸出層采用Bayes分類規則,選出具有最大后驗概率的類別作為輸出的類別。
判定規則如式(16)所示。
Hilifi(X)>Hjljfj(X),則X∈Mi
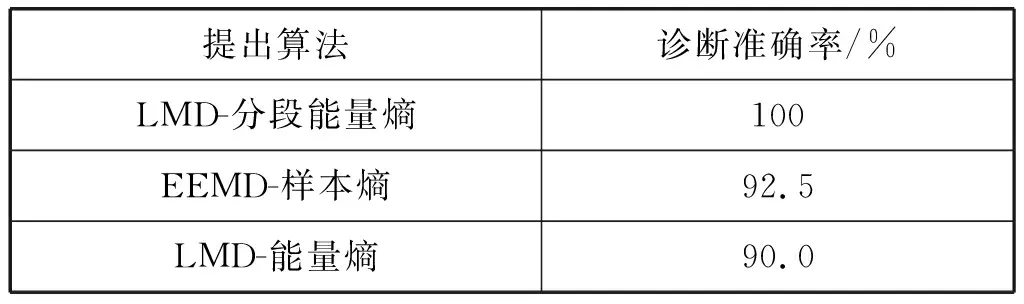
Hilifi(X) (16) 式中:Hi、Hj為故障類型Mi、Mj的先驗概率,Hi=li/L,Hj=lj/L;li、lj為Mi、Mj的訓練樣本數。 DE算法優化PNN參數是將PNN測試樣本的均方誤差作為DE算法的適應度函數(RMSE),得到最優的平滑因子,優化步驟如下: (1) 設置差分進化算法參數,進化代數、交叉概率、變異概率等相關參數。 (2) 選取PNN輸出結果的均方誤差(RMSE)作為適應度函數,隨機生成群空間個體。 (3) 實現變異、交叉操作。 (4) 實現選擇操作、比較適應度值,并更新參數代數。 (5) 如果沒有滿足終止條件(未達到最大迭代次數或結果小于預定結果),則代數加1,并返回步驟(2);否則,繼續執行下列步驟。 (6) 得出最小均方誤差時對應的最優平滑因子參數并輸出。 (7) 得到最優平滑因子參數下的故障診斷結果。 本文利用LMD算法分解原始信號,計算LMD分解后的每個PF分量與原始信號的相關系數,篩選多余分量并進行信號重構,通過計算重構信號的分段能量熵組成特征向量,并且輸入到DE優化的PNN模型進行故障診斷。其識別過程如圖4所示。 圖4 故障診斷總體流程 (1) 模擬斷路器故障,利用拾音器采集動作時的音頻數據,歸一化處理后取故障后的10 000個點作為故障數據。 (2) 對于選中的數據進行LMD分解。 (3) 計算每個PF分量與原始信號的相關系數參數,選取適當的分量重構信號。 (4) 計算重構信號的分段能量熵,并按照順序排列作為故障特征向量W,建立故障特征向量樣本集。 (5) 利用DE優化概率神經網絡(PNN)并對斷路器機械故障樣本集進行訓練與測試,并得到測試結果。 在實驗室10 kV戶內真空高壓斷路器(ZN-63A)上采集數據,如圖5所示。模擬合閘動作時的螺絲松動、傳動機構卡澀和合閘彈簧儲能不足三種故障狀態與正常合閘動作狀態,采集相應各個狀態聲音信號數據。 圖5 10 kV戶內高壓真空斷路器故障采集平臺 文獻[8]中指出斷路器聲音信號的主要頻段分布在0~2 kHz之間。拾音器采用高性能心型電容話筒得勝CM-63(頻率范圍30~20 000 Hz)進行音頻數據采集,采樣頻率44 100 Hz。四種狀態數據在MATLAB中歸一化之后的波形如圖6所示。 圖6 四種狀態原始數據歸一化波形 實驗采用螺絲松動、傳動機構卡澀和合閘彈簧儲能不足與正常合閘動作四種狀態數據進行分析,每種狀態采集30組實驗數據,并將樣本數據中的20組作為訓練集,10組作為測試集,利用DE優化后的PNN對訓練集進行模型訓練與測試。DE算法參數最大進化次數為100,變異因子為0.4,交叉因子為0.2。 DE優化得到的參數平滑因子spread為0.919 4。將四種狀態共80組訓練樣本集輸入概率神經網絡進行模型訓練。 將四種狀態的數據測試樣本集輸入斷路器機械故障診斷模型,進行故障診斷。故障診斷結果如圖7所示。 圖7 測試集測試結果 可以看出,DE-PNN算法對傳動機構卡澀、合閘彈簧儲能不足、螺絲松動三種狀態能夠準確地診斷故障類型,此時平均識別準確率能達到100%,實驗證明本文算法對于斷路器聲音信號能有良好的診斷效果。 為了驗證DE-PNN相較于其他分類方法的優勢,選取選用未改進的PNN、極限學習機(Extreme Learning Machine,ELM)和BP神經網絡對同等數據特征樣本集進行模型訓練與測試。 多次實驗選擇PNN的平滑因子參數為0.91,ELM隱含層參數為50,BP神經網絡隱含層節點數為34。診斷結果如表2所示。 表2 四種分類算法的性能對比 可以看出,在對同等故障特征樣本集進行測試時,DE優化后的PNN相較于傳統PNN算法提升了5百分點的故障識別準確率,驗證了DE優化算法的性能,相較于ELM和BP算法分別提升了20百分點以及5百分點的算法準確率,驗證了本文提出的DE優化PNN方法的優勢。 為驗證本文提取算法的有效性,選取文獻[19-20]中的特征提取算法與本文提出的算法作對比,利用DE優化后的PNN模型對故障進行診斷。結果如表3所示。 表3 各種常見算法與本文算法對比結果 可以看出,本文算法相較于其他常見的算法來說,具有更好的特征提取效果,在對于故障樣本集進行測試時得到更高的故障診斷準確率,驗證了本文算法的有效性。 本文提出一種基于LMD和DE-PNN的高壓斷路器機械故障診斷方法。通過對高壓斷路器合閘時的故障聲音信號進行LMD分解,依據各個PF分量與原信號的相關系數選取合適的PF分量進行重構,計算重構后的信號的分段能量熵并按順序排列作為斷路器故障特征向量構建故障特征樣本集,建立基于DE-PNN故障診斷模型并進行訓練與測試,實現了高壓斷路器機械故障診斷。實驗結果表明: (1) 基于LMD-DE-PNN的斷路器機械故障診斷方法,能一定程度上抑制信號背景噪聲、濾除多余干擾、提升特征提取效果、得到較好的故障診斷正確率。 (2) DE-PNN相較于未改進的PNN時,提升了5百分點的故障診斷正確率,驗證了差分進化算法的優化性能,相較于ELM和BP算法,在斷路器機械故障診斷時分別提高20百分點和5百分點的故障診斷正確率,并且診斷速度較快,適用于斷路器聲音診斷領域。 (3) 本文提出的LMD分段能量熵相較于EEMD-樣本熵和LMD-能量熵分別提高了7.5百分點與10百分點的故障診斷準確率,驗證了本文算法的有效性。 本文描述了非線性非平穩的斷路器故障聲音數據分析方法與故障診斷模型的建立過程,實驗驗證本文方法具有較好的故障診斷效果,為基于聲音信號的斷路器機械故障診斷提供了一種新的思路。2.3 DE優化PNN參數
3 基于LMD和DE-PNN的故障診斷方法
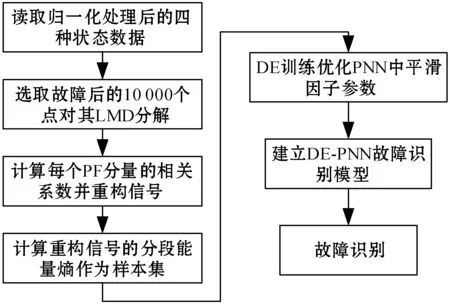
4 實驗分析

4.1 DE-PNN模型訓練與測試
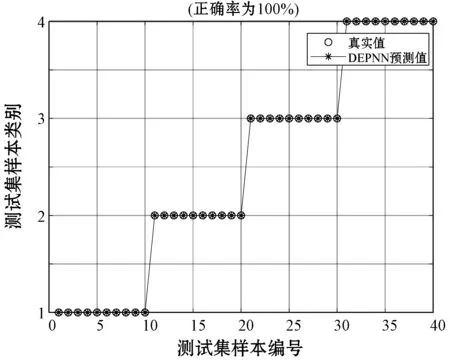
4.2 分類算法性能分析
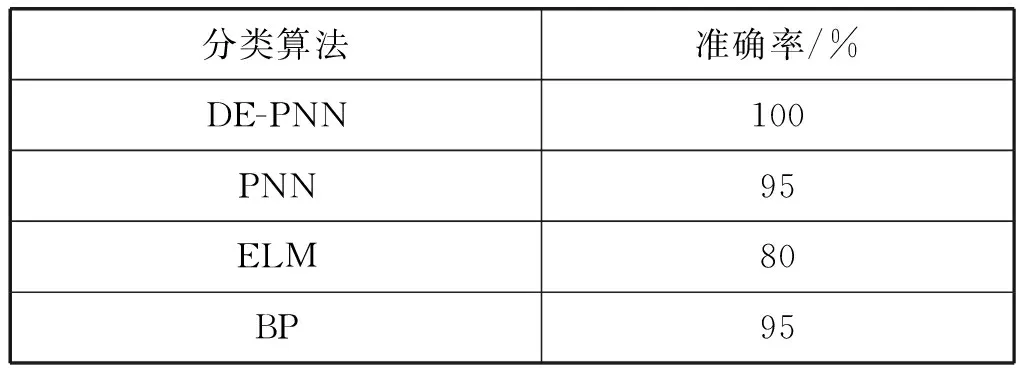
4.3 特征提取算法分析對比
5 結 語

