基于非平衡問題的卷積神經(jīng)網(wǎng)絡分類模型

矯桂娥 徐 紅 張文俊 陳一民

1(上海大學上海電影學院 上海 200072) 2(上海海洋大學信息學院 上海 201306) 3(上海建橋學院信息技術學院 上海 201306)

0 引 言

在現(xiàn)實生活中,數(shù)據(jù)集的分布都不是理想的均衡分布,更多的是呈現(xiàn)非平衡分布特性。非平衡問題是指在數(shù)據(jù)集中不同類別的數(shù)據(jù)分布差異較大,即存在樣本數(shù)量多的多數(shù)類以及樣本數(shù)量少的少數(shù)類。在分類任務中,傳統(tǒng)的分類學習器適合類別平衡分布的數(shù)據(jù)集,而對于存在非平衡問題的數(shù)據(jù)集,往往受多數(shù)類的影響而導致少數(shù)類分類出現(xiàn)錯誤。但實際應用中,少數(shù)類樣本的有效分類卻是極其重要的,比如銀行用戶詐騙檢測、醫(yī)療疾病診斷、客戶流失檢測、設備故障檢測等等[1-5]。因此,準確地判別少數(shù)類是非平衡分類問題的一項重要研究內容,目前,研究學者對該類問題的解決方法主要集中在數(shù)據(jù)以及算法兩個層面。

在數(shù)據(jù)層面上,需要對數(shù)據(jù)進行初步的分析采樣,以達到數(shù)據(jù)分布平衡目的。但是這種簡單的方式生成的新樣本具有很大的不確定性,生成的少數(shù)類樣本質量不高,極易產(chǎn)生過擬合問題。為了解決這一問題,Devi等[6]提出了CorrOV-CSEn算法,將過采樣與集成算法AdaBoot相結合,欠采樣算法通過舍棄部分多數(shù)類樣本達到樣本類別平衡,而過采樣算法是依據(jù)某些規(guī)律增加少數(shù)類樣本以達到平衡不同類別,但效果欠佳。熊炫睿等[7]提出了SABER采樣算法,將簇內樣本平均分類錯誤率考慮到采樣算法中。Park等[8]采用融合過采樣與欠采樣的算法COUSS處理非平衡數(shù)據(jù)分類問題,但效果不理想。趙錦陽等[9]提出了SCSMOTE方法,通過在少數(shù)類樣本中選擇出合適的首選樣本,在樣本中心和候選樣本中間生成新樣本,克服了簡單生成新樣本的缺陷,可以避免一定的過擬合,但是該方法合成的新樣本有一定的重復性,部分樣本會變成噪聲樣本。因此,有部分研究學者在此基礎上將SMOTE和欠采樣方法相結合,對少數(shù)類進行SMOTE過采樣,在多數(shù)類中進行隨機欠采樣,該方法不會過多地生成新的少數(shù)類樣本,從一定層面上降低了樣本噪聲的影響。于艷麗等[10]提出了基于異類k距離的邊界混合采樣算法BHSK,首先異類k距離識別邊界,再通過支持度將邊界數(shù)據(jù)細分,最后依次采樣。Li等[11]提出了根據(jù)損失值來確定可以參與訓練的樣本的采樣方法,該方法對數(shù)據(jù)集中數(shù)據(jù)依據(jù)樣本損失值加權,在抽樣操作中被選中的概率由樣本權重決定。以上這些方法都是在數(shù)據(jù)層面的調整,讓數(shù)據(jù)在輸入分類模型前就分布平衡,因此很多數(shù)據(jù)集的樣本分布規(guī)律與生成類過采樣算法生成樣本所依據(jù)的規(guī)律并不相關,所以按照這種過采樣方法生成的樣本會有很大概率生成噪聲樣本,這樣的采樣方法非但起不到提高檢測少數(shù)類精確率的效果,還會對多數(shù)類的判別產(chǎn)生混淆影響,從而影響分類效果,并且降低多數(shù)類的正確率。

卷積神經(jīng)網(wǎng)絡是深度學習領域中最出色的網(wǎng)絡結構,應用在計算機的各領域中,比如圖片分類[12]、目標跟蹤[13]和自然語言[14]等方面,因此近年來非平衡問題的研究學者也采用卷積神經(jīng)網(wǎng)絡解決此類問題。卷積神經(jīng)網(wǎng)絡模型以損失函數(shù)最小為目標,所以在卷積神經(jīng)網(wǎng)絡處理非平衡數(shù)據(jù)分類問題時,對于不同類別的數(shù)據(jù)賦予不同的損失權重,以此更新卷積神經(jīng)網(wǎng)絡的損失函數(shù),以達到損失函數(shù)最小化的目的。周麗娜等[15]使用卷積神經(jīng)網(wǎng)絡處理文本分類時,采用特征融合結合交叉熵損失函數(shù);Niu等[16]提出了一種代價敏感重構損失函數(shù),并對引入了正則項;張士川等[17]采用代價敏感損失函數(shù)結合孿生網(wǎng)絡對暗星系進行分類檢測;Miao等[18]在軟件缺陷檢測中采用代價敏感函數(shù),對不同的樣本賦予不同的損失權重。以上是在算法層面對非平衡數(shù)據(jù)分類問題的研究,但是,上述數(shù)據(jù)預處理算法只是較為適應數(shù)據(jù)集,并不能與分類模型更好地融合,損失函數(shù)也不能與采樣函數(shù)相結合發(fā)揮最佳的效果。為此我們提出了一種卷積神經(jīng)網(wǎng)絡分類模型CNN-EMWRA-WCELF(Convolutional Neural Network-Expectation Maximization Weighted Resampling Algorithm-Weight Cross Entropy Loss Function),模型中有兩個關鍵算法,其中EMWRA算法對數(shù)據(jù)集進行采樣,該算法對EM算法進行了改進優(yōu)化,巧妙地將加權采樣算法融合進了高斯混合模型中,通過本文所提的EMWRA算法對數(shù)據(jù)進行預處理,明顯降低了訓練數(shù)據(jù)集的不平衡程度。由于EMWRA算法在對原始數(shù)據(jù)的選擇上更加注重少數(shù)類的分布特征,采樣高質量的少數(shù)類新樣本,避免了生成大量噪聲樣本的弊端,使模型分類效果更好。另外,通過本文所提的WCELF函數(shù)根據(jù)訓練樣本的分類結果和真實標簽,反饋模型的損失,以此達到提升非平衡數(shù)據(jù)分類準確率。CNN-EMWRA-WCELF模型解決了上述改進的非平衡問題的采樣數(shù)據(jù)混淆模型分類等單一算法對非平衡問題的缺點和不足。

1 本文算法

本文中的分類模型采用的是卷積神經(jīng)網(wǎng)絡模型,在數(shù)據(jù)預處理階段提出將加權采樣算法融合進高斯混合模型中,得到了一種新的EMWRA算法,綜合考慮了數(shù)據(jù)集中的樣本分布,對少數(shù)類樣本進行更精確地過采樣,經(jīng)過卷積神經(jīng)網(wǎng)絡的訓練,損失函數(shù)WCELF作為衡量模型分類結果和真實標簽的差異程度的目標函數(shù),將根據(jù)模型對輸出的分類結果賦予樣本相應的權重損失并反饋給模型,模型依據(jù)損失函數(shù)進行下一輪的訓練,以此逐步提高模型對于非平衡數(shù)據(jù)的分類準確性。

CNN-EMWRA-WCELF模型如圖1所示:對非平衡數(shù)據(jù)的分類,本文用到的是卷積神經(jīng)網(wǎng)絡模型,在數(shù)據(jù)預處理階段,EMWRA算法將數(shù)據(jù)按照其整體分布劃分為小的高斯混合分類簇,并按照每個簇中的樣本分布進行加權采樣,將各分類簇中的采樣集傳入卷積神經(jīng)網(wǎng)絡分類模型中進行分類訓練,再根據(jù)分類結果依照真實分類結果計算損失函數(shù),最后將結果反饋到卷積神經(jīng)網(wǎng)絡中,并以此修改EMWRA采樣結果。

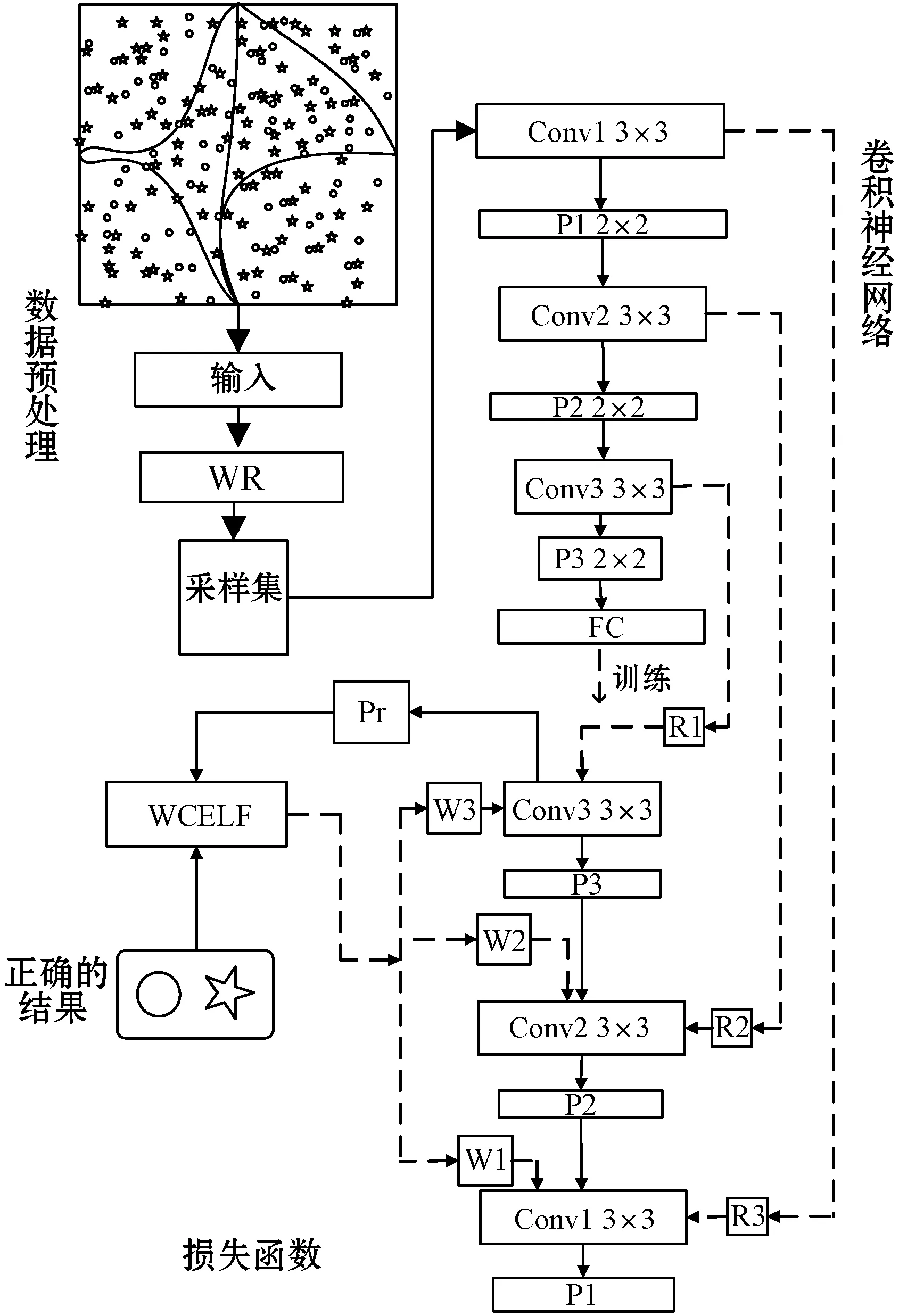
圖1 CNN-EMWRA-WCELF模型示意圖

本文的EMWRA-WCELF算法的流程如圖2所示。可以看出,EMWRA-WCELF具體包括:在訓練的初始輸入數(shù)據(jù)集;設定模型訓練采樣集的大小;高斯混合模型對數(shù)據(jù)集進行初步分類;根據(jù)高斯混合模型原理,通過EM算法求得最佳高斯混合模型的參數(shù),進而得到最佳高斯混合簇;在對每個混合簇進行采樣的過程中,會判斷簇中的樣本分布是否平衡,對樣本分布不同的混合簇,有不同的采樣方式;在完成對每個混合簇的采樣后,將所有的采樣結果匯聚到采樣集中,分類模型對最終的采樣集進行學習訓練;WCELF函數(shù)根據(jù)模型分類結果和樣本真實標簽,計算損失函數(shù),并反饋給分類模型;如果損失函數(shù)上升或者達到了模型訓練的最好結果,訓練就會停止,將模型的訓練參數(shù)保存。

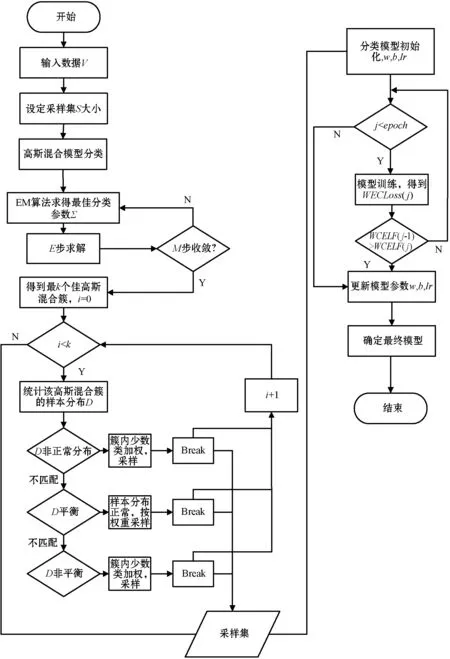
圖2 EMWRA-WCELF算法流程

1.1 EMWRA

1.1.1 高斯混合模型及核心算法

高斯混合模型[19]是一種概率密度聚類算法,在預測數(shù)據(jù)分布概率方面有較好的分類效果。高斯混合模型對整個數(shù)據(jù)集的擬合能力主要依賴于它的構成,高斯混合模型是由多個高斯單模型組成,這一特性可以較好地擬合實際中的數(shù)據(jù)集,其核心算法是EM算法。EM算法是一類通過迭代進行最大似然估計的優(yōu)化算法,可以有效地避免數(shù)據(jù)中的噪聲和混合成分所帶來的局限性。

因為高斯混合模型的對數(shù)據(jù)集的整體分布的概括能力,所以我們在采樣的初始階段,用它擬合數(shù)據(jù)集。設數(shù)據(jù)集X為n維數(shù)據(jù),服從高斯分布,其概率密度函數(shù)可表示為:

(1)

式中:μ為數(shù)據(jù)均值,Σ為n×n協(xié)方差矩陣,由此可以將其記錄為P(x|μ,Σ)。

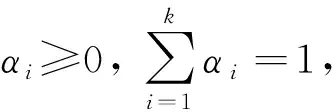
(2)

1.1.2EM算法改進提升EMWRA

我們在高斯混合模型核心算法EM基礎上對其進行了改進,得到了一種新的算法EMWRA。

在高斯混合模型中,根據(jù)數(shù)據(jù)的先驗分布α1,α2,…,αk采樣混合樣本,我們將混合系數(shù)αi表示為采樣自第i個高斯混合成分的概率,采樣數(shù)據(jù)集D={d1,d2,…,dn}為在高斯混合模型中采樣產(chǎn)生的數(shù)據(jù)集,設φj∈{1,2,…,k}表示高斯混合簇di的隨機變量,其先驗概率為P(φj=i)=αi,φj的后驗概率根據(jù)貝葉斯公式為:

(3)

根據(jù)式(2),式(3)可表示為:

(4)

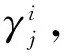
(5)

(6)

(7)

高斯混合算法是高斯混合模型的一種迭代算法,它是根據(jù)每個樣本點的概率分布對其進行劃分,不同于傳統(tǒng)的聚類算法根據(jù)距離等因素對數(shù)據(jù)進行類,EM算法是依據(jù)它們歸屬于哪一類而進行劃分,所以這種分類策略更適應于復雜數(shù)據(jù)。

傳統(tǒng)加權采樣方法是從m個樣本集中依據(jù)樣本權重選擇s個樣本,每個樣本被選中的概率由其相對權重決定,樣本ζ被選中的概率如式(8)所示。

(8)

EMWRA在數(shù)據(jù)預處理階段,高斯混合模型將數(shù)據(jù)集劃分為一些簇,每個高斯混合分類簇中的數(shù)據(jù)是不同的。在劃分結果中數(shù)據(jù)可能服從于不同的高斯分布,在每個簇中各類樣本的概率分布確定多數(shù)類和少數(shù)類的交叉情況。

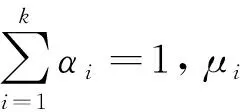
在高斯混合分類簇中,少數(shù)類樣本的均值μs和多數(shù)類樣本的均值μd,數(shù)據(jù)量Q=QS+Qd,樣本集的類別分布比例可表示為β=QS/Q。令βi=Qis/Qi,其中i表示是第i個高斯分類簇,i={1,2,…,k}。Qis表示該混合簇中的少數(shù)類樣本數(shù)據(jù)量,βi表示高斯混合簇中的非平衡樣本比例。

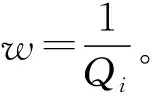
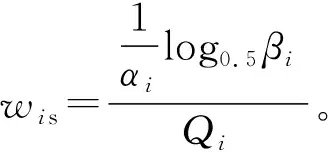
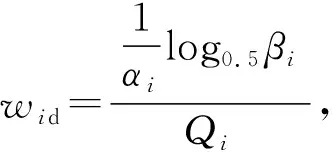
符合情況(2)和(3)的混合簇的樣本采樣概率計算如式(9)所示。

(9)

每個混合簇采樣數(shù)量由混合系數(shù)αi確定,數(shù)據(jù)分布不平衡的混合簇中,簇中的少數(shù)類樣本會依據(jù)其權重進行采樣。

這樣可以根據(jù)數(shù)據(jù)集的整體概率分布,劃分出最佳的簇,其中根據(jù)αi可以得出整個數(shù)據(jù)的分布,αi為整個高斯過程的權重,它的大小體現(xiàn)了樣本集中的大多數(shù)數(shù)據(jù)的分布范圍,可以更加全面地統(tǒng)計樣本信息。EMWRA有效避免了對少數(shù)類樣本進行采樣而產(chǎn)生的噪聲樣本,有效提高了模型對非平衡數(shù)據(jù)集的分類準確度。

1.2 WCELF函數(shù)

為提升卷積神經(jīng)網(wǎng)絡對非平衡數(shù)據(jù)集的分類性能,在模型的訓練過程中,能夠根據(jù)預測結果與真實標簽的差距,得到最佳的模型損失函數(shù),本文提出了一種基于權重交叉熵損失WCELF函數(shù),該損失函數(shù)是描述模型分類結果與真實樣本標簽差距的函數(shù)。在二分類任務中,最常用的損失函數(shù)是交叉熵損失函數(shù),但是在非平衡分類任務中,該損失函數(shù)的效果難以達到最好。因此,我們針對非平衡問題提出了結合樣本權重的損失函數(shù)WCELF。

交叉熵損失函數(shù)[20]一般通用的公式如式(10)所示。

(10)

這里的tθ是樣本的真實類別,yθ是模型的預測結果,交叉熵損失函數(shù)的大小表示兩者的差距。當模型預測值與真實值越接近時,它對應的損失值就越小,分類模型的損失也就越大,值得注意的是,這種損失值的增大是非線性的,由其自身log函數(shù)的特性呈現(xiàn)指數(shù)增長。

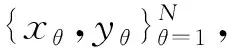
δi=log1.1βi

(11)

式中:βi表示的是樣本所在高斯混合簇中的樣本分布,在這里i={1,2,…,k}。當該log函數(shù)的自變量大于1時,保證了少數(shù)類別的權重不過高導致模型分類失衡。

添加了權重的交叉熵損失函數(shù)如下:

(12)

WCELF函數(shù)根據(jù)非平衡數(shù)據(jù)集的高斯混合簇中的數(shù)據(jù)分布情況,自適應更新每個高斯混合簇中的樣本損失權重。該損失函數(shù)在計算訓練樣本的網(wǎng)絡輸出值與樣本真實標簽的同時,考慮樣本所在的高斯混合簇,易分類的多數(shù)類樣本的預測值yp→1,1-yp→0,如此,分類模型的Lwce→0,這確保了多數(shù)類的損失相對較少。但是對于部分非正常非平衡高斯混合簇,該簇中的少數(shù)類為原始數(shù)據(jù)集中的多數(shù)類,所以該損失函數(shù)中δζ會對該高斯混合簇中的多數(shù)類賦予一定的代價損失。然而,對于少數(shù)類樣本預測值yp→0,1-yp→1,且該損失函數(shù)考慮到了高斯混合簇中的樣本分布δζ,結合EMWRA合理地增加了少數(shù)類的代價損失,對非平衡數(shù)據(jù)分類有積極的影響,但是在提升模型對少數(shù)類樣本分類精確度的同時,沒有降低對多數(shù)類數(shù)據(jù)的分類效果。

損失權重的計算會根據(jù)采樣值的不同進行自適應更改,根據(jù)不同分類簇中的不同樣本采樣權重,給予不同的損失權重。在此過程中對于部分在高斯混合簇中的非正常不平衡數(shù)據(jù)集中的多數(shù)類,實行同樣的少數(shù)類損失權重。該損失函數(shù)很好地避免了分類模型在平衡少數(shù)類樣本時,忽略部分易錯多數(shù)類樣本的情況,可以更進一步提升分類模型的準確率。

對該損失函數(shù)進行求導可得:

(13)

初始化神經(jīng)網(wǎng)絡模型,按照訓練epoch訓練數(shù)據(jù)集,根據(jù)輸出結果統(tǒng)計樣本分類正確率,依照類別權重分別賦予不同樣本損失,將損失函數(shù)反饋到分類模型中,模型按照式(13)更新得到最佳參數(shù),從而逐步提高分類準確率,最終得到一個最優(yōu)結果。

2 實驗結果與分析

2.1 實驗數(shù)據(jù)集

本文使用kaggle競賽數(shù)據(jù)集churn(電信用戶流失數(shù)據(jù))和Model_churning(銀行客戶流失數(shù)據(jù))進行實驗,數(shù)據(jù)集對客戶是否留存進行了分類,這兩個數(shù)據(jù)集屬于典型的非平衡問題的數(shù)據(jù)集。

2.2 評價指標

為更好地處理非平衡數(shù)據(jù)的分類問題,更全面地衡量模型的分類性能,評價標準既要保證分類的準確率也要保證少數(shù)類分類的正確性。本文采用混淆矩陣的三級指標F1調和平均值和G-mean這兩個評價標準對模型進行評估,F1的值可以從整體上反映分類的性能,G-mean是用于衡量非平衡數(shù)據(jù)分類效果的指標。

2.3 實驗過程

本文采用PyTorch深度學習框架,搭建卷積神經(jīng)網(wǎng)絡分類學習模型,為降低模型的分類過擬合,在模型訓練過程中相對應添加了dropout層,參數(shù)為0.5,訓練集、驗證機與測試集的比例為8∶1∶1,batch_size設置為512。

2.4 實驗結果分析

CNN-EMWRA-WCELF卷積神經(jīng)網(wǎng)絡模型的分類結果主要是和整體分類模型的數(shù)據(jù)分類結果作比較,其中集成學習方法是對結構化數(shù)據(jù)較為常用的方法,在過往許多kaggle數(shù)據(jù)比賽成果中,獲勝方法都會用到集成學習算法。編碼方案采用的是one-hot編碼,本文通過競賽數(shù)據(jù)集來驗證本文提出的卷積神經(jīng)網(wǎng)絡模型CNN-EMWRA-WCELF的分類性能。

在churn和Model_churning兩個數(shù)據(jù)集上,本文對加權損失函數(shù)和卷積神經(jīng)網(wǎng)絡在非平衡數(shù)據(jù)的處理做了對比實驗。

損失函數(shù)比較結果如圖3所示,實線表示交叉熵損失函數(shù),虛線表示W(wǎng)CELF損失函數(shù)。損失函數(shù)總體都在下降,在銀行客戶分類中損失函數(shù)的差別更為明顯,相差在0.2左右。由此可見對損失函數(shù)添加類別權重能夠很好地降低模型損失,提升模型的分類性能。

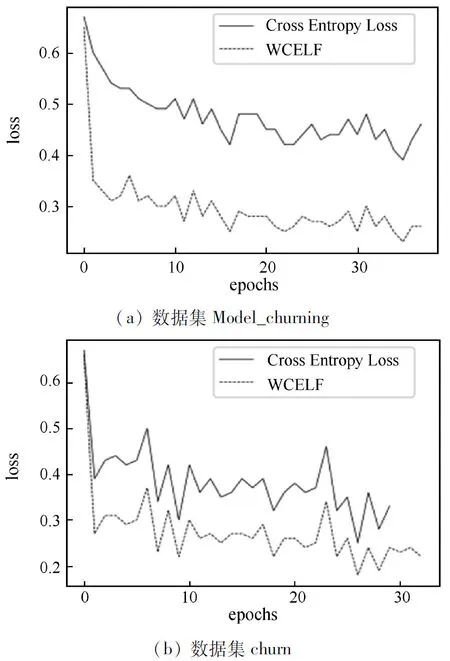
圖3 損失函數(shù)對比

本文的對照模型是參照文獻[7]中的SABER采樣算法,分別結合邏輯回歸、隨機森林,還有集成學習分類模型XGBoost,如LRSABER(邏輯回歸SABER分類模型)、RFSABER(隨機森林SABER分類模型)、SVMSABER(支持向量機SABER分類模型)、XGBoostSABER(XGBoostSABER分類模型),文獻[8]中COUSS采樣算法LRCOUSS(邏輯回歸COUSS分類模型)、SVMCOUSS(支持向量機COUSS分類模型)等。以上模型都是經(jīng)典的分類模型,應用范圍較廣,其中XGBoost模型采用了集成學習思想,這種集弱學習器之長處成強學習器的思想應用在很多數(shù)據(jù)分析競賽中,分類效果很好。為體現(xiàn)本文所提算法對神經(jīng)網(wǎng)絡分類性能有所提升,所以本文設置了對卷積網(wǎng)絡的對比,首先對比的是在兩個數(shù)據(jù)集上采樣算法在分類指標F1和G-mean上的表現(xiàn),其中CNNSABER(卷積神經(jīng)網(wǎng)絡SABER分類模型)、CNNCOUSS(卷積神經(jīng)網(wǎng)絡COUSS分類模型)和CNNAdaptive-SMOTE(卷積神經(jīng)網(wǎng)絡Adaptive-SMOTE分類模型)是卷積神經(jīng)網(wǎng)絡結合各采樣算法的分類模型。表1是上述各分類模型與各采樣算法在churn數(shù)據(jù)集上的分類效果對比。其中CNN-EMWRA-WCELF是本文所提的分類模型。

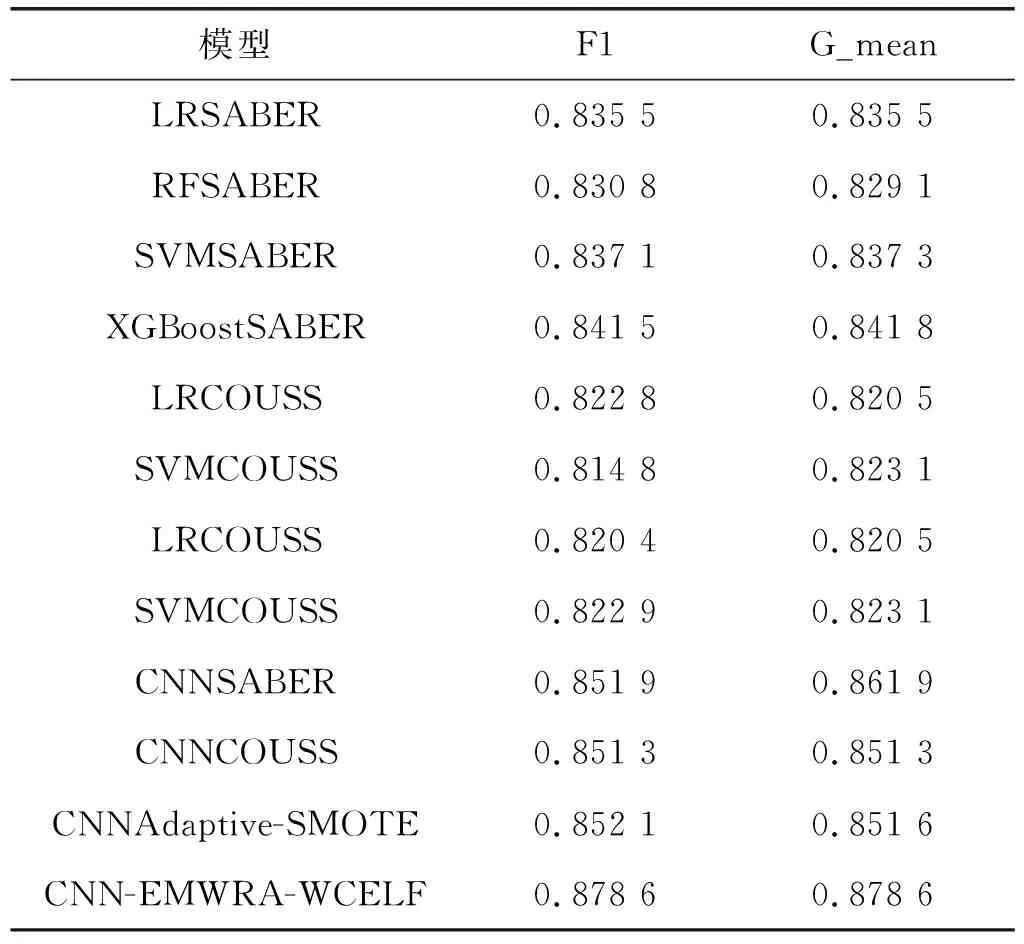
表1 在數(shù)據(jù)集churn上實驗結果

表1中的結果顯示了在邏輯回歸、支持向量機等傳統(tǒng)機器分類模型和卷積神經(jīng)網(wǎng)絡模型結合了SABER和COUSS等采樣算法在kaggle電信客戶分類數(shù)據(jù)集上的分類效果。可以得出在F1調和平均值和G-mean值兩個評測指標中,卷積神經(jīng)網(wǎng)絡模型的分類性能相比較傳統(tǒng)機器學習分類模型有約2%～4%的提升,這個對比結果表明因其高效的特征提取能力,卷積神經(jīng)網(wǎng)絡在數(shù)據(jù)挖掘和數(shù)據(jù)分析領域更有優(yōu)勢。在對比采樣算法在卷積神經(jīng)網(wǎng)絡模型上的分類效果的三組對比實驗中,本文所提采樣算法EMWRA讓卷積神經(jīng)網(wǎng)絡的分類性能在此基礎上又提升了近2%,由這個對比結果可以得出,我們提出的分類模型CNN-EMWRA-WCELF在非平衡數(shù)據(jù)集中的表現(xiàn)比結合SABER和COUSS等采樣算法的分類模型更好。

如表2所示,在銀行客戶數(shù)據(jù)集中的結果分析與比較中可以發(fā)現(xiàn),卷積神經(jīng)網(wǎng)絡模型的分類評價指標較傳統(tǒng)機器學習如支持向量機等有4%～15%的效果提升,本文的采樣算法使得卷積神經(jīng)網(wǎng)絡在評價指標F1和G-mean上提升近2%。而且僅對比卷積神經(jīng)網(wǎng)絡的實驗結果也可以看出,簡單生成少數(shù)類的采樣方法算法會產(chǎn)生一些噪聲樣本,降低模型的分類性能。簡單來說,相較于XGBoost等集成分類模型,卷積神經(jīng)網(wǎng)絡模型效果更好一些,而采樣算法EMWRA讓卷積神經(jīng)網(wǎng)絡的分類性能又提升了2%,在該數(shù)據(jù)集上CNN-EMWRA-WCELF分類模型的優(yōu)勢更為明顯。

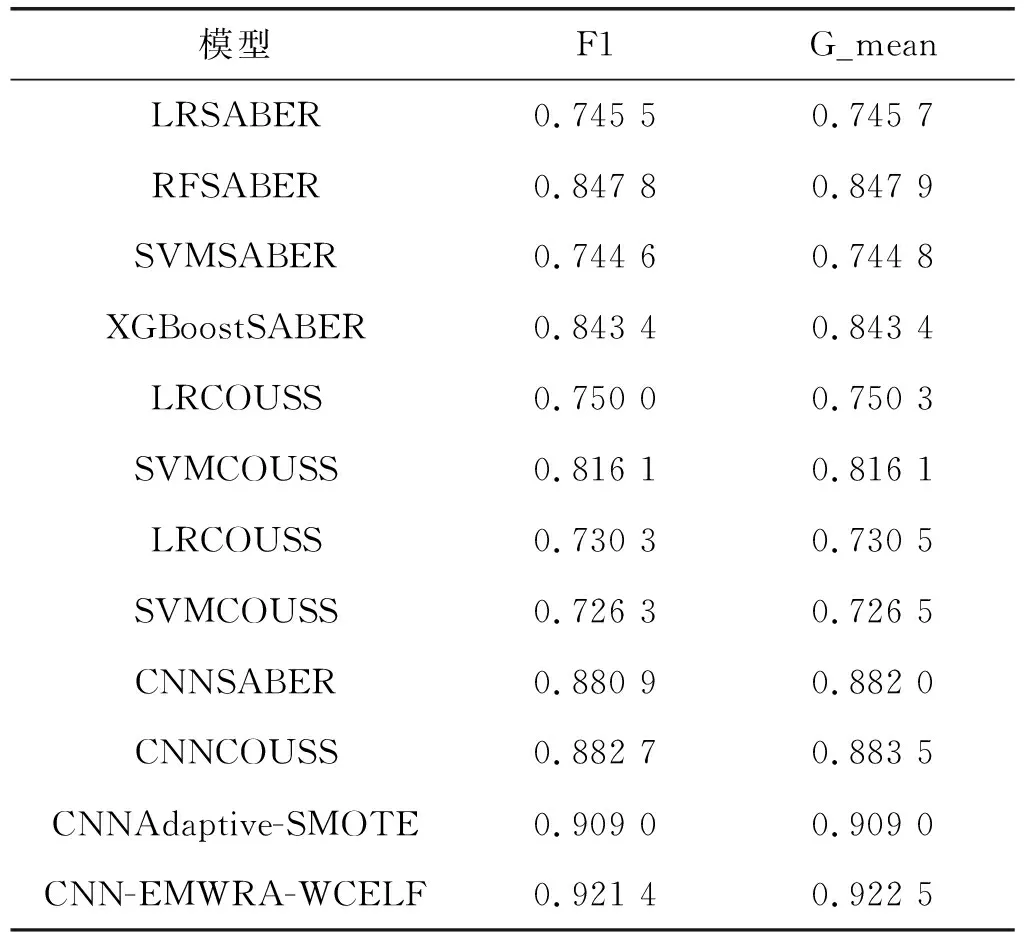
表2 在數(shù)據(jù)集Model_churning上實驗對比

3 結 論

在非平衡分類問題的研究中,本文提出的CNN-EMWRA-WCELF分類模型,其中EMWRA是結合高斯混合模型和加權采樣的采樣方法,該采樣算法可以很好地處理樣本空間類別重疊的數(shù)據(jù)集,提升了采樣的少數(shù)類樣本的質量,除此之外還對數(shù)據(jù)集進行加權采樣,使采樣集內數(shù)據(jù)達到類別分布平衡;損失函數(shù)WCELF作為衡量模型分類結果和真實標簽的差異程度的目標函數(shù),將根據(jù)模型對輸出的分類結果賦予樣本相應的權重損失并反饋給模型,模型依據(jù)損失函數(shù)進行下一輪的訓練,由此可不斷提高模型對于非平衡數(shù)據(jù)的分類準確性。從本文的實驗結果來看,卷積神經(jīng)網(wǎng)絡在非平衡數(shù)據(jù)問題中有著出色的表現(xiàn),這也驗證了近年來研究學者將卷積神經(jīng)網(wǎng)絡應用到非平衡問題中的正確性。除此之外,本文提出的模型整體效果也比其他模型好很多。后續(xù)的工作是研究多分類的非平衡分類問題,為處理現(xiàn)實生活中的更多實際問題做出貢獻。