十字型通道內黏彈性撞擊流混合機理研究

徐旭東，張 巍，李偉鋒，劉海峰，王輔臣

（華東理工大學上海煤氣化工程技術研究中心，上海 200237）

流體混合強化是傳熱[1]、納米材料制備[2]、生物醫藥[3]及乳液制備[4]等許多工業應用的關鍵研究內容。設備微型化旨在用更小、成本更低、效率更高的設備或工藝取代大型、昂貴、能源密集型設備或工藝，這是當前化工行業的發展趨勢。由于能顯著強化流體混合，化工裝置微通道內的撞擊流動近年來備受青睞。因此，對微通道內復雜撞擊流動及混合機理進行研究具有理論意義和應用價值。

作為典型的微通道，十字型微通道由兩個垂直交叉的通道組成，近年來被廣泛研究。Haward 等[5-6]結合顯微成像和激光誘導熒光（PLIF）技術研究了十字型微通道內流動模式及吞噬流結構。研究結果表明，十字型微通道內吞噬流主要以中心渦為特征，中心渦的形成是由渦拉伸效應驅動的。隨著微通道深度的增加，吞噬流將會出現在更低的雷諾數下。本課題組Zhang 等[7]采用類似的實驗手段研究了厘米尺度下十字型微通道內的流動和混合機理，并結合數值模擬發現了由渦破裂導致的流體循環區域。以上研究結果皆基于牛頓流體，然而在實際應用中的液體更為復雜，它們往往同時具有彈性和黏性，并表現出與牛頓流體不同的流動特性，例如：在兩個旋轉圓柱縫隙（Taylor-Couette）中的黏彈性流體發生的混沌流動[8]；低雷諾數下黏彈性流體在T 型微通道中的三維振蕩行為[9]；在黏彈性流體的圓柱繞流中，彈性所產生的擾動會向上游傳播，從而使得上游變得不穩定導致出現雙穩態流型[10-11]；在兩平行板間的黏彈性流動中，即使流速很低，當流體彈性足夠大時流動也會變得不規則[12]；以及在黏彈性圓管流動中，流體彈性會導致低雷諾數下管內出現類湍流[13-15]。

在十字型微通道中，即使微量聚合物的加入都可以對流動產生顯著影響，因此眾多學者開展了大量關于黏彈性流體流動特征的研究。Arratia 等[16]研究了十字型微通道內低濃度聚丙烯酰胺溶液的流動，發現在雷諾數極低（Re＜0.01）時十字型微通道內出現了一種穩態非對稱的流動。Poole 等[17]使用麥克斯韋模型對該現象進行了數值模擬，結果表明低雷諾數下的流動失穩是由流體彈性驅動的。Rocha等[18]使用有限可擴展非線性彈性模型（Finitely Extensible Nonlinear Elastic，FENE）研究了十字型微通道內聚合物濃度和聚合物鏈拉伸長度對流動穩定性的影響，結果顯示隨著聚合物濃度或分子拉伸長度的增加，流動失穩的臨界維森貝格數（Wi）減小。Cruz 等[19]接著使用3 種不同黏彈性模型研究了十字型微通道內的流動，給出了十字型微通道內的流型轉換的臨界參數。Sousa 等[20]利用聚丙烯酰胺溶液和甘油溶液，研究了十字型微通道內聚合物溶液濃度對流動模式的影響。實驗結果表明，只有當聚合物溶液濃度較高時，穩態非對稱流型才出現。Burshtein等[21]在十字型微通道中研究了聚合物溶液濃度的影響。結果發現，隨流體彈性系數增大，黏彈性流體比牛頓流體在更低臨界雷諾數下失穩。Qin 等[22]利用全息粒子跟蹤的方法，確定了彈性流動的三維結構。Haward 等[23]在十字型微通道中通過改變溶液性質研究了不同EI（EI=Wi/Re）下通道內的流動模式。當EI＞1 時，穩態對稱流動在Wi超過臨界值時轉變為穩態非對稱流動；當EI＜1 時，發現了一系列瞬態不穩定性，流動顯示出高頻振蕩。以上研究工作表明微通道內黏彈性流體的流動模式及其特征十分復雜，流體性質及通道結構參數的變化均會導致黏彈性流動的顯著改變，但是對于不同尺度下的十字型通道內的黏彈性流體的流動及混合機理尚不清晰，因此有必要對其進行系統研究。

本文采用PLIF 研究了十字型通道內牛頓流體和黏彈性流體的流動特征，旨在揭示流體黏彈性對流動穩定性及混合機理的影響。在寬度為500 μm、6 mm、1 cm 這3 種尺度的十字型通道內對比了水和不同質量分數聚環氧乙烷（PEO）溶液的流動模式、振蕩特征以及混合效果。本文提供了一種使用黏彈性流體強化混合的方式，為撞擊流通道的設計開發及應用提供了指導。

1 實驗方法

1.1 實驗流程及微通道結構

實驗流程如圖1（a）所示，通過兩臺能夠使用流量控制儀進行流量設定和控制的注射泵（RSP01-BD 型，流量范圍為1.57×10-7～5.80×102mL/min，兩側入口流量偏差小于0.1%）將流體定量注入微通道內，實驗中流入管路足夠長（大于100 倍入口管道直徑）以消除注射泵引起的脈動。流體在中心區域撞擊后沿兩個出口通道流出并最終流入儲液罐。通過流量控制儀來控制入口流量。十字型通道結構如圖1（b）所示，寬度（W）和深度（H）相等，為保證流動充分發展，進出口通道長度為15W。為了探究十字型通道尺度的影響，W分別取500 μm、6 mm 和1 cm。

圖1 （a）實驗流程圖及（b）十字型通道示意圖Fig.1 Schematic diagram of (a) experimental flow chart and (b) cross-shaped channel

利用PLIF 技術對十字型通道進行可視化研究，所用流體為純水和PEO（平均分子量為4×106）溶液。流體經由注射泵注入通道中，其中注射泵B 注入的流體中加入了0.15 mg/L的染色劑羅丹明6G（其對流體性質的影響可以忽略不計）。實驗使用Nd:YAG固態脈沖式激光器（頻率為10 Hz），羅丹明6G 在激光照射下會發射出波長為532 nm 的熒光信號，使用帶有濾光片的CCD（Charge Coupled Device）相機捕捉熒光信號，濾光片能夠減少自然光和激光的干擾。捕捉到的熒光信號經轉化器轉化為數字信號后，在電腦上進行實時觀測，并通過PLIF 系統的Dantec studio 軟件進行數據處理。

1.2 流體性質

實驗用PEO 溶液的質量分數分別為0.01%、0.03%、0.10%和0.30%，其制備方法和相關物性參數和文獻[21]一致。制備PEO 溶液時為了幫助聚合物粉末溶解，同時避免PEO 機械降解，采用低速人工攪拌直到液體中沒有折射率變化或看不到殘留的凝膠。不同質量分數PEO 溶液的黏度（η）和弛豫時間（λ）如表1 所示，純水的黏度（η0）為1.005 mPa·s，實驗在室溫（（20±5）℃）下進行。

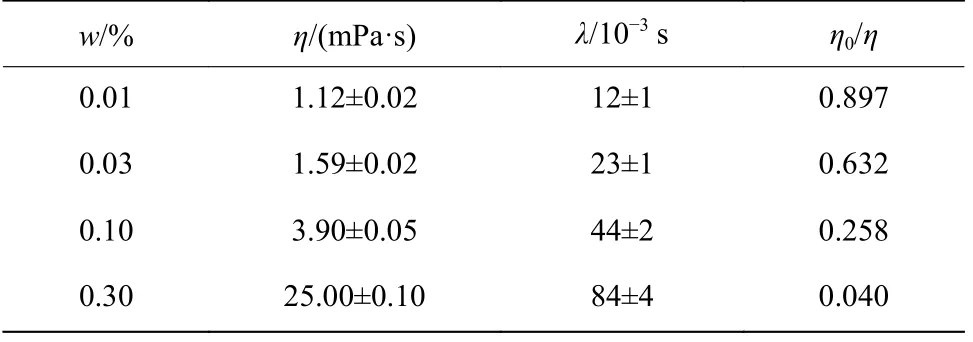
表1 PEO 溶液流體性質參數Table 1 Fluid property parameters of PEO solutions

本文用雷諾數和維森貝格數來描述慣性、黏性和彈性力的相對大小。雷諾數用來表示慣性力和黏性力的相對大小，其定義為：

維森貝格數描述了彈性與黏性力的相對大小，可以表示為：

2 結果與討論

2.1 流動可視化結果

圖2 所示為純水在500 μm 十字型微通道中的流動模式，箭頭為流體的進出方向，右側縱坐標為出口通道的空間標尺。當雷諾數較低（Re=20）時微通道中呈對稱的分離流模式，如圖2（a）所示。隨著雷諾數增加，穩態吞噬流的流型出現，此時兩股流體相互卷吸，如圖2（b）所示。當Re=270 時，腔室內出現非穩態渦脫落振蕩，該模式下靠近通道中心的區域基本保持穩定，而在下游發生以渦旋脫落為特征的高頻軸向振蕩，如圖2（c）所示。當雷諾數增加到300 以上，微通道內發生周期性的渦合并振蕩，形成非穩態吞噬流，如圖2（d）所示。

圖2 500 μm 十字型微通道內純水流動模式Fig.2 Flow patterns for pure water in the cross-shaped channel of 500 μm

隨著聚合物溶液的加入，微通道內出現了不同于純水在通道中的流型。當聚合物溶液質量分數較低時，通道內流體不斷地抖動，在更低的雷諾數（Re=42）下失穩，這增強了通道內的混合效果。如圖3（a）～3（c）所示（圖中t0為流體振蕩的初始時刻），此時通道內流動雖然有吞噬流特征，但是受到流體彈性影響，觀察到的流體條紋結構并不如純水中清晰。當雷諾數增大到126，彈性效應增強，兩股流體撞擊后形成的中心渦不斷收縮擴張，如圖3（d）～3（f）所示（圖中t0為流體振蕩的初始時刻）。由于在該模式（圖3（d）～3（f））下，流動由慣性和彈性共同作用導致，因此將該模式稱為慣性彈性非穩態振蕩。

圖3 500 μm 十字型微通道內慣性彈性非穩態振蕩的PLIF 圖（w=0.03%）Fig.3 PLIF images of inertial elastic unsteady oscillations in the cross-shaped channel of 500 μm (w=0.03%)

隨著聚合物溶液質量分數（w）繼續增加，微通道內流體彈性占據主導。圖4 所示為PLIF 瞬時圖（圖中T0表示彈性非穩態振蕩的周期）。當w=0.30%和Re=0.37 時，流動開始失穩，此時流動以染色和未染色流體之間的界面橫向振蕩為特征，且振蕩具有良好的周期性。由于微通道內雷諾數極低，慣性的影響微弱，此時通道內的流動不穩定性主要由流體彈性驅動，因此將該模式稱為彈性非穩態振蕩。這種彈性不穩定性的發生是因為聚合物分子具有拉伸效應，產生的拉伸應力使得流線的曲率變小，這導致入口流體進入中心區域后不再垂直向出口流出，而是向著對角的方向流動，因此形成了這種界面的橫向振蕩[24]。

圖4 PLIF 瞬時圖（Re=0.37，Wi=2.26，w=0.30%）Fig.4 Instantaneous PLIF snapshots (Re=0.37, Wi=2.26, w=0.30%)

圖5（a）為500 μm 微通道內不同質量分數聚合物溶液的流動模式相圖。結果表明，微通道內主要呈現6 種流型，分別是分離流、穩態吞噬流、渦脫落振蕩、非穩態吞噬流、慣性彈性非穩態振蕩和彈性非穩態振蕩。當雷諾數較低時，微通道內都呈現出穩態對稱的分離流模式。在低聚合物溶液質量分數（w=0.01%）下，通道內展現出了與純水（η0/η）=1.0 不同的流動模式，隨著雷諾數增加，通道內出現了慣性彈性非穩態振蕩且并未出現其他流動模式；當聚合物溶液質量分數增加到0.03%時，該模式的臨界雷諾數從24 降低到17。當w=0.10%（η0/η=0.258）時，慣性彈性非穩態振蕩消失，微通道內出現了由彈性主導的非穩態振蕩；當聚合物溶液質量分數從0.10%增大到0.30%（η0/η=0.040），彈性非穩態振蕩的臨界雷諾數從29 降低到0.37，流動在極低雷諾數下就失穩。

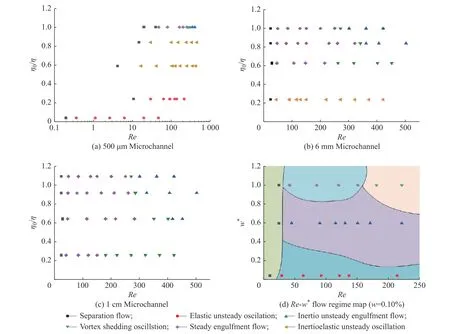
圖5 不同質量分數聚合物溶液和不同通道尺度下的流動模式相圖Fig.5 Map describing flow patterns with different mass fractions of polymer solution and channel sizes

對于6 mm 十字型通道，當聚合物溶液質量分數為0.01%（η0/η=0.897）時，此時流動模式和水類似，出現分離流、穩態吞噬流、渦脫落振蕩和非穩態吞噬流，但是受到彈性影響，流型的臨界雷諾數發生變化，渦脫落振蕩的臨界雷諾數從270 增大到340，非穩態吞噬流的臨界雷諾數從300 增大到360，見圖5（b）。當聚合物溶液質量分數為0.03%（η0/η=0.632）時，非穩態吞噬流消失，進一步增加聚合物溶液質量分數到0.10%，通道內流動呈現慣性彈性非穩態振蕩模式，如圖5（d）所示，圖中w*為量綱為一的通道水力直徑，其數值是采用最大通道的水力直徑（1 cm）進行量綱為一化得到的。

對于1 cm 十字型通道，與500 μm 通道和6 mm通道內的流動不同，實驗中并未觀察到慣性彈性非穩態振蕩或彈性非穩態振蕩的流動模式，但是受到彈性的影響，通道內渦脫落振蕩和非穩態吞噬流的臨界雷諾數隨著聚合物溶液質量分數的增加而增大，且在聚合物溶液質量分數為0.10%時非穩態吞噬流消失（圖5（c）～圖5（d）所示）。以上結果表明，在相同聚合物溶液質量分數下，隨著十字型通道尺度的增大，彈性起到的作用越發微弱，這說明尺度的增加會削弱彈性的影響。

2.2 非穩態振蕩特性

為了定量表征在500 μm 十字型微通道內的彈性非穩態振蕩模式，對z/W=0 平面上La（y/W=1）以及Lb（y/W=-1）兩條線上的平均濃度的時間序列進行了統計，如圖6（a）所示。對于縱坐標，其中為某條線上羅丹明6G 溶液的平均濃度，c0為入口羅丹明6G 溶液的濃度。從圖6（a）可以看出，兩個出口中的濃度分布波形相似。因此，僅選擇一個出口通道濃度的時間序列就可以分析其振蕩規律。從圖6 中可以發現，在低Wi時，振蕩表現出良好的周期性特征，且隨著Wi的增加，振蕩周期減小。當Wi=2.26 時，周期（T）約為3.85 s，當Wi為11.26 和22.51 時，周期分別減小到3.63 s 和2.00 s。進一步增大Wi數，腔室內的流體振蕩逐漸變得不規則，如圖6（g）和6（h）所示。

圖6 歸一化濃度變化的時間序列及其功率譜（w=0.30%）Fig.6 Time series of normalized concentration and corresponding spectra (w=0.30%)

為了比較不同工況下十字型通道內流體的振蕩，統計了不同雷諾數下的斯特勞哈爾數（St=f Dh/u，f為微通道中振蕩的頻率），結果如圖7 所示。可以看出，對于微通道中黏彈性流體誘導的彈性非穩態振蕩模式，其斯特勞哈爾數隨雷諾數的增大而減小。對于1 cm 的十字型通道，不同質量分數下斯特勞哈爾數都隨雷諾數的增大而減小。隨著聚合物溶液質量分數的增加，斯特勞哈爾數變大，且斯特勞哈爾數比500 μm 十字型微通道中大了兩個數量級，由此可以看出，這兩種分別由慣性和彈性主導的振蕩機理本質不同。對于慣性主導的非穩態吞噬流，其周期性自持振蕩形成的原因是由于撞擊面上高壓流體對中心渦內低壓流體的擠壓而引發的旋渦破碎[7]；而對于彈性主導的非穩態振蕩，其形成的原因是由于兩股黏彈性流體撞擊后所產生的彈性應力使得出口通道內速度場發生偏斜[24]。

圖7 不同質量分數流體的斯特勞哈爾數隨雷諾數的變化Fig.7 Strouhal numbers for different mass fractions of fluids at various Reynolds number

2.3 混合效果評價

圖8 示出3 種尺度下x-y平面不同質量分數流體Is值其中c為瞬時羅丹明6G 溶液的濃度，c為平均濃度，c′為濃度偏差，為濃度方差）隨雷諾數的變化情況。結果表明，在500 μm 微通道內，當聚合物溶液質量分數為0.01%時，受到彈性影響，慣性彈性非穩態振蕩出現，加強了混合效果，因此Is值比純水低。而在彈性非穩態振蕩（w＞0.10%）中，低雷諾數下其Is值相比分離流略低，混合效果相比水較好，這是因為彈性主導的非穩態振蕩增加了流體界面面積。隨著雷諾數增加，流動始終呈現彈性非穩態振蕩，和低聚合物質量分數下的慣性彈性模式相比，其混合效果變差。需要指出的是，當w=0.03%和Re＞126 時，盡管此時依然為慣性彈性振蕩，但彈性效應顯著增強（如圖3（d）～3（f）所示），導致Is值升高，整體混合效果下降。

圖8 3 種尺度通道內不同質量分數流體Is 隨雷諾數的變化Fig.8 Is varies with Reynolds numbers for different mass fractions of fluids in three different channel sizes

對于1 cm 十字型通道，不同聚合物溶液質量分數下其混合效果變化趨勢基本與水類似。結合圖5（c）和圖8（c）可以看出，當處于穩態分離流時，Is較大；當穩態吞噬流出現后，Is明顯降低。當流動處于渦脫落振蕩和非穩態吞噬流模式時混合效果進一步增強。可以看出黏彈性流體的加入對混合效果的影響并不大，這說明通道尺度的增大逐漸削弱了流體彈性的影響。對于6 mm 十字型通道，隨著聚合物溶液質量分數增加，特別是w=0.10%時，由于發生了慣性彈性非穩態振蕩，其混合效果相比水顯著增強。

3 結 論

在500 μm 十字型微通道中，不同于純水在其中的流動模式，當聚合物溶液質量分數為0.01%時，慣性彈性非穩態振蕩出現；當聚合物溶液質量分數增大到0.10%時，慣性彈性非穩態振蕩消失，微通道內出現了彈性主導的非穩態振蕩模式。對于6 mm 十字型通道，隨著聚合物溶液質量分數的增大，渦脫落振蕩和非穩態吞噬流的臨界雷諾數增大；當聚合物溶液質量分數增大到0.03%時，非穩態吞噬流消失；當聚合物溶液質量分數為0.10%時，出現了慣性彈性非穩態振蕩。對于1 cm 十字型通道，變化趨勢與6 mm 相同，但由于尺度更大，受到彈性的影響更小，當聚合物溶液質量分數為0.10%時非穩態吞噬流才消失，且并未出現慣性彈性非穩態振蕩。

對于彈性非穩態振蕩，該模式在維森貝格數和雷諾數較低時具有周期性特征，隨著維森貝格數和雷諾數增大，斯特勞哈爾數減小，振蕩周期減小，且趨于不規則。對于非穩態吞噬流，斯特勞哈爾數隨著雷諾數的增大而減小，隨著聚合物溶液質量分數的增加而變大，且斯特勞哈爾數比彈性非穩態振蕩大了兩個數量級，說明彈性非穩態振蕩與非穩態吞噬流本質不同。

在500 μm 十字型微通道中加入w為0.01%的聚合物溶液即可使得慣性彈性非穩態振蕩發生，從而加強混合；當聚合物溶液質量分數增大到0.03%，慣性彈性非穩態振蕩的臨界雷諾數降低，流動在更低雷諾數下失穩，混合進一步加強；對于6 mm 十字型通道，加入相對較高質量分數的聚合物溶液也可以達到混合強化的效果；但對于1 cm 十字形通道，聚合物溶液的加入對混合效果的影響并不大。