面向超材料微結構的離散變量拓撲優化設計①

劉宏亮,蔣亦煌,梁 緣,王培金,郝 鵬

(1.沈陽航空航天大學 航空宇航學院,遼寧省飛行器復合材料結構分析與仿真重點實驗室,沈陽 110136;2.大連理工大學 工程力學系, 工業裝備結構分析國家重點實驗室,大連 116023)

0 引言

具有周期性微結構組成的超材料結構憑借其優異的力學性能以及獨特的物理性能在航空航天領域展現出廣闊的應用前景。例如,運載火箭、載人飛船、人造衛星等航天器在服役過程中對結構輕量化和高性能化的需求不斷增加,因此具有特異性能且輕質的超材料結構獲得了越來越廣泛的關注。事實上,微結構的幾何形狀和物理性能往往決定了由其組成的宏觀構型的力學性質,這就使得微結構設計具有重要的學術意義和應用價值。隨著高新科技的不斷發展,增材制造等先進技術變得愈來愈成熟,具有復雜構型的微結構也可以被制造出來,從而進一步促進超材料設計[1],而這也推動了航空航天裝備的前沿研究和應用發展。

在眾多設計方法中,拓撲優化技術通過在給定的設計區域內尋求材料的最佳分布使得約束條件下的結構性能最優,是一種有效獲得新型微結構構型的方法。近年來,結構拓撲優化技術被廣泛應用于眾多工程領域,已成為結構創新設計的有效途徑[2-4]。目前被廣泛采用的拓撲優化方法主要有固體各向同性材料懲罰法(Solid Isotropic Material with Penalization, SIMP)[2, 5]、水平集方法(Level Set Method,LSM)[6-7]、漸進結構優化方法(Evolutionary Structural Optimization,ESO)[8-9]和移動可變形組件方法(Moving Morphable Components, MMC)[10]等。

對于由周期性微結構單胞組成的宏觀結構材料,其每一點的有效物理性質可以由數值均勻化方法獲得[11]。BENDS?E和KIKUCHI[12]通過使用漸近均勻化方法對結構中不同位置的微結構進行尺寸優化,從而優化出整體的拓撲結構。在漸近均勻化方法的基礎上,多種可設計微觀結構的拓撲優化方法被成功地擴展到周期性微結構設計中。例如,RADMAN等[13]采用漸進優化方法以及LI等[14]采用水平集方法設計出了具有特定性能的周期性功能梯度微結構。值得指出,SIMP方法因其概念簡單、易于實現且計算效率高的特點被廣泛應用于超材料微結構設計。SIGMUND[15]將SIMP方法和逆均勻化方法相結合設計出具有特定本構參數的微結構。隨后,SIGMUND和TORQUATO[16-18]進一步設計出了具有特定熱膨脹系數和壓電系數的微結構。另外,SIMP方法還被用于具有特定力學性能的手性材料設計[19],同時滿足零膨脹和高剛度的多功能性單胞構型設計[20-22]以及最大滲透率設計[23]。XIA和BREITKOPF[24]使用了能量均勻化方法計算單胞的等效力學性能,并結合密度法獲得了三種不同目標的微結構設計,與漸近均勻化方法相比,該方法具有計算效率高的優點。需要說明的是,SIMP方法由于使用連續變量,在計算過程中會存在中間密度,即使增大懲罰因子,中間密度也難以被完全消除,這會一定程度上損害優化結果的目標值,還會影響結構的可制造性[25]。

本文工作致力于獲得清晰的超材料微結構構型設計,從而為提取和控制結構的幾何信息提供便利,促進結構設計和制造過程的深度融合。本文采用能量均勻化方法,在此基礎上研究了基于離散變量方法[26-27]的結構體積約束下的微結構設計。根據不同的初始設計,獲得體積模量最大化和剪切模量最大化的微結構構型設計。數值算例用于說明本文優化設計的有效性,并研究了初始設計和體積約束對微結構離散變量拓撲設計構型的影響。

1 能量等效均勻化

1.1 基于能量等效均勻化的等效性質計算

(1)

根據單元應變能,可以將式(1)改寫為[15]

(2)

基于有限元分析,將微結構離散成N個單元,則式(2)可以修改為

(3)

對于二維結構設計問題,等效本構張量可以寫為如下表達式:

(4)

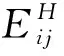
(5)

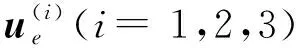
1.2 周期性邊界條件

超材料往往在結構中周期性排布,因此需要在單胞上施加周期性邊界條件以獲得單胞的等效性質。根據文獻[28]所述,邊界上的周期性條件可表示為

(6)

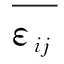
值得指出,需要將式(6)轉換成為一種更顯式的周期性邊界條件[29]。考慮圖1所示的微結構,一組相對邊界上的位移為

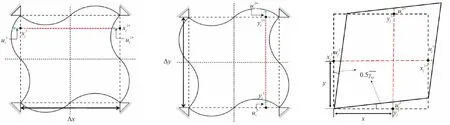
(a) Applying horizontal unit strain (b) Applying unit strain in vertical direction (c)Applying unit shear strain圖1 施加不同應變后的周期性微結構變形示意圖Fig.1 Schematic diagram of periodic microstructure deformation after applying different strains

(7)

在二維設計問題中,上標k分別表示垂直于水平或豎直方向的邊界面。通過將式(7)中的兩式相減,可得到如下關系式:

(8)

(9)

(10)

如圖1(c)所示,施加單位剪切應變時,左右對邊水平方向自由度位移與上下對邊豎直方向自由度位移需要滿足:

(11)

2 離散變量下的超材料設計優化列式及其求解

本文考慮體積約束下微結構設計的離散變量拓撲優化列式如式(12)所示:

(12)

式中C為單胞等效性質的目標函數;K(ρ)為結構的總體剛度矩陣。

由于離散變量的特點是無需進行剛度懲罰,因此總體剛度矩陣與設計變量的關系可以表示為

(13)

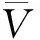
本文的設計目標是考慮體積模量和剪切模量最大化。對于體積模量最大化設計問題,相應的目標函數可以定義為

(14)

對于剪切模量最大化設計問題,其目標函數可以定義為

(15)

優化列式(12)是目標函數的隱式函數,本文將使用靈敏度信息將式(12)顯式化。

當考慮體積模量最大化設計問題時,目標函數的離散變量靈敏度可以采用如下表達式計算:

當考慮剪切模量最大化設計問題時,目標函數的離散變量靈敏度的計算表達式為

(17)

為了消除棋盤格式,本文采用如下形式的線性靈敏度過濾(以體積模量為例):

(18)

其中,

Hij=max(0,rmin-Δ(i,j))

式中rmin為濾波半徑;Δ(i,j)為單元i與單元j中心點的距離。

為了求解大規模非線性整數規劃問題,采用序列近似整數規劃和正則松弛算法求解,利用目標函數的離散變量靈敏度將原隱式優化問題轉化為如下形式的顯式規劃問題[26]:

(19)

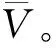
3 數值算例

本節基于兩種不同的初始設計構型給出微結構設計中離散變量方法的數值結果與討論。其中,材料彈性模量取為E0=1,泊松比ν= 0.3,初始設計區域如圖2所示。

(a)Circular hole (b)Square hole圖2 初始設計區域Fig.2 Initial design domain

3.1 體積模量最大化設計

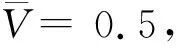
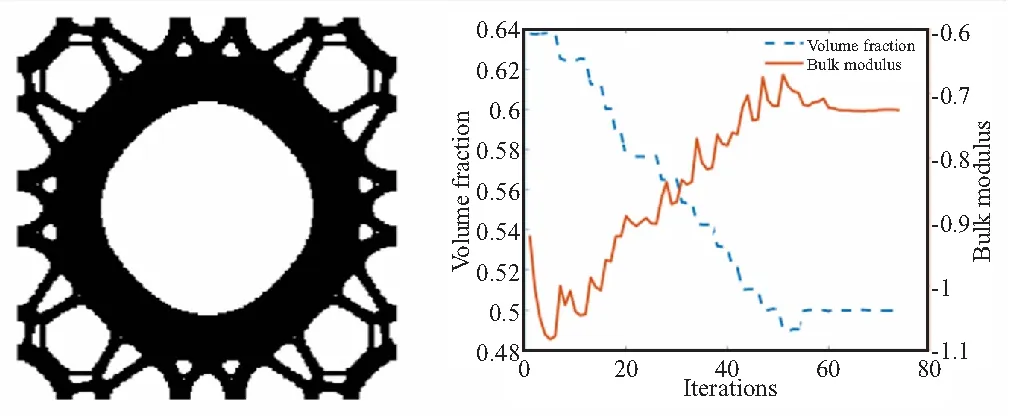
(a)Optimization result and iterative curve of initial design with circular hole

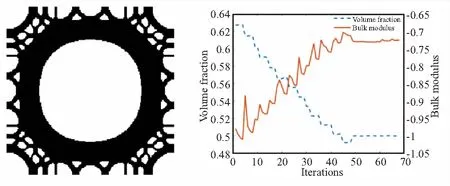
(b)Optimization result and iterative curve of initial design with square hole圖3 體積模量最大化設計結果及迭代曲線Fig.3 Optimization results and iteration curves of bulk modulus maximization

(a)Optimization result of initial design with circular hole (b)Optimization result of initialdesign with square hole圖4 體積模量最大化優化結果(SIMP方法Fig.4 Optimization results of bulk modulus maximization

圖5 體積模量最大化優化結果及迭代曲線Fig.5 optimiation resuits and iteration curves of buik moduius maximization

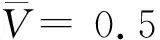
圖6 體積模量最大化的初始設計及優化結果Fig.6 Initial design and optimization results for bulk modulus maximization

基于圖6(a)的初始設計,經迭代計算后分別得到圖6(b)、(c)的兩種矩形微結構,兩者收斂設計的目標函數值分別為0.725 4和0.225 9。對比之前計算得到的正四邊形微結構,目標函數值相差較小。

3.2 剪切模量最大化設計

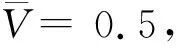
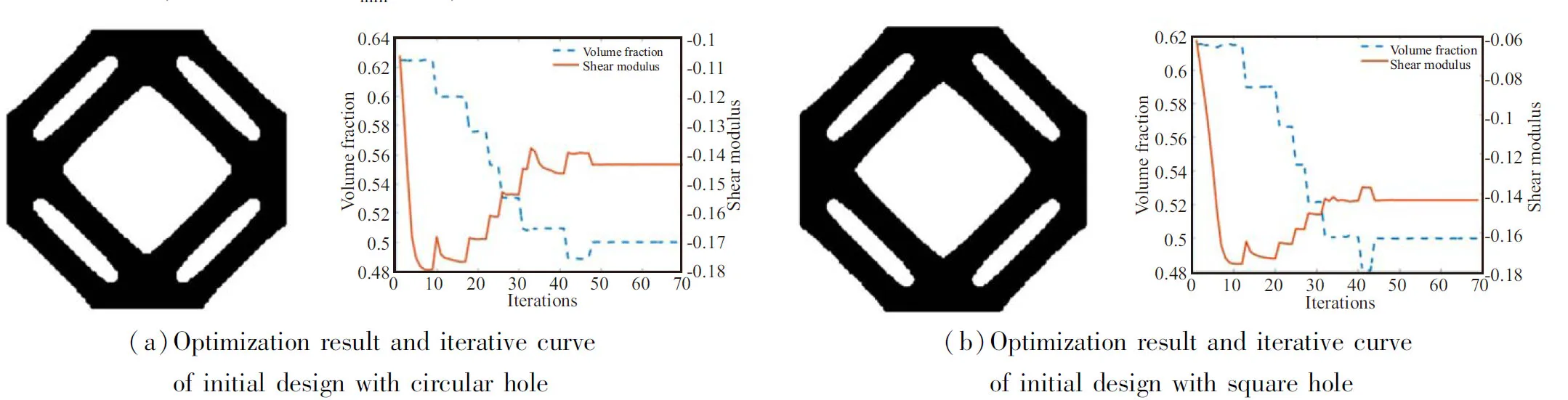
圖7 剪切模量最大化優化結果及迭代曲線Fig.7 Optimization results and iteration curves of shear moduius maximization

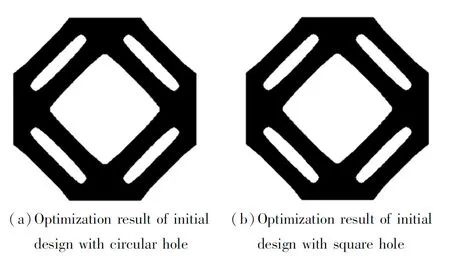
圖8 網格加密后剪切模量最大化優化結果Fig.8 Optimization results of shear modulus maximizationafter mesh 0.5)

圖9 剪切模量最大化優化結果及迭代曲線Fig.7 Optimization results and iteration curves of shear moduius maximization

另外,將圖2中初始設計的圓孔和方孔分別改為原來孔洞大小的14.9%和11.1%,初始設計和優化結果如圖10所示,相應的目標函數值分別收斂于0.137 2和0.139 9。從優化結果可以看出,當初始設計改變后,優化出的微結構在外部輪廓上具有相似之處,但結構的內部構造完全不同。可見,當選取不同的初始設計時,會存在設計出微結構構型不一致的情況。對比圖7的優化結果圖可以發現,圖10的優化結果存在較多的孔洞,這意味著整體結構的剛度會略差于前者,而且計算出的目標函數值可以進一步表明圖7的兩種微結構構型的剛度更優。

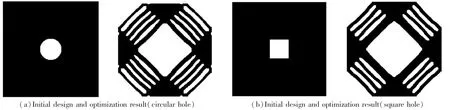
圖10 剪切模量最大化的初始設計及優化結果Fig.10 Initial design and optimization results for shear modulus maximization

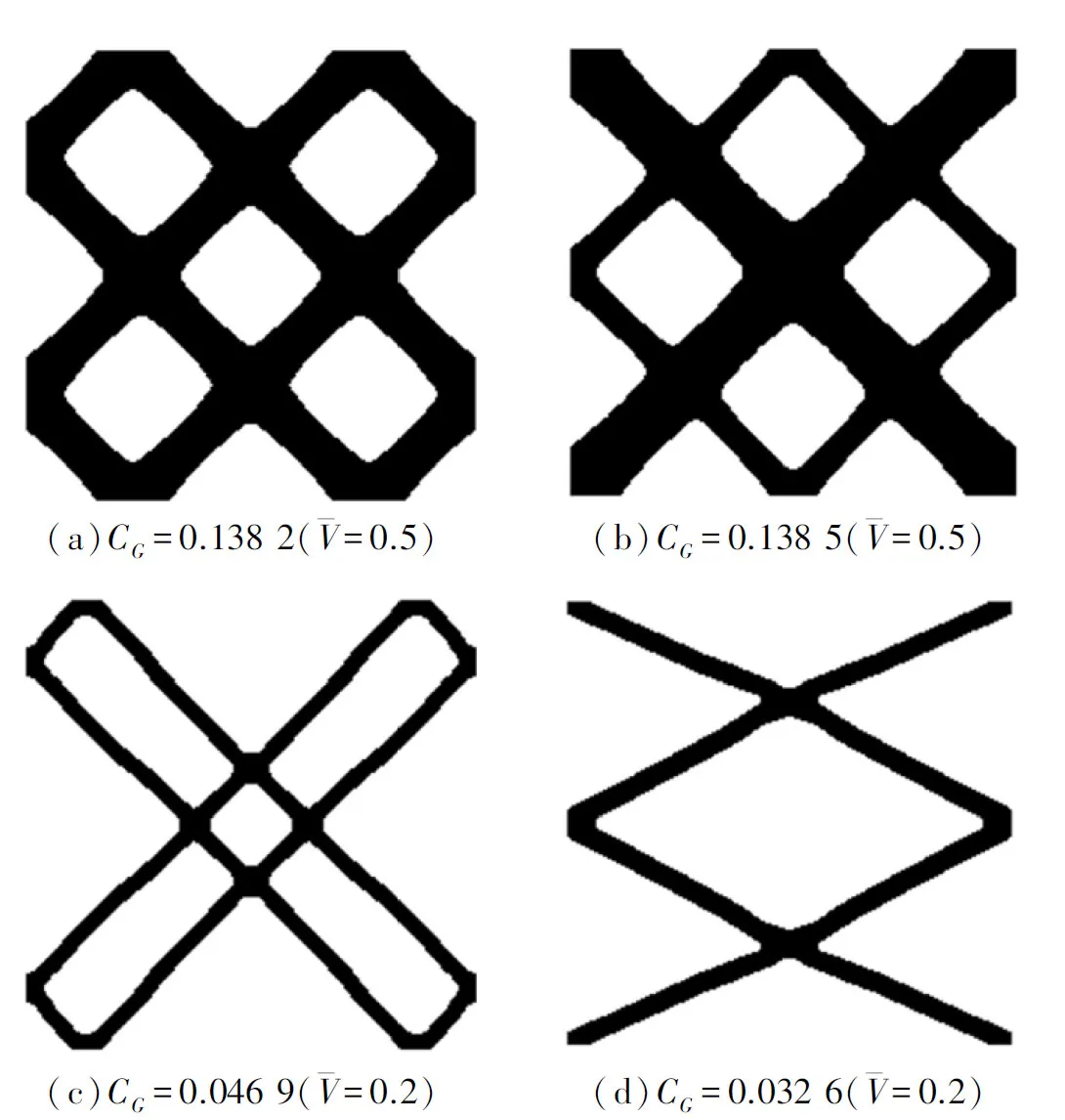
圖11 剪切模量最大化優化結果Fig.11 Optimization results of shear modulus maximization

4 結論

本文面向新型輕質飛行器結構設計中的超材料微結構拓撲優化,在能量均勻化方法的基礎上利用序列近似整數規劃和正則松弛算法實現了超材料微結構的離散變量拓撲優化設計。結論如下:

(1)根據兩種初始孔洞設計構型和隨機初始設計,求解了材料體積約束下體積模量最大化和剪切模量最大化兩種結構性能目標的優化問題,驗證了方法的有效性,獲得了新型微結構設計。

(2)數值算例結果表明基于離散變量的微結構拓撲優化設計能夠有效避免灰度模糊問題。另外,結構的初始設計和材料體積約束對優化結果的影響較大,考慮不同性能目標的微結構設計構型的差異明顯。