窄頻差硅基環形陀螺檢測閉環控制系統設計

劉宇鵬,崔 讓,郭瀟林,劉 學,張 越,曹慧亮

(1. 中北大學電子測試技術重點實驗室,太原 030051; 2.山西北方機械制造有限責任公司,太原 030009)

0 引言

微型半球諧振陀螺(micro-hemispherical reson-ator gyro, MHRG) 傳承了傳統半球諧振陀螺(hemispherical resonator gyro, HRG) 高精度的優點[1],并融合了微機電系統(micro-electro-mechanical system, MEMS)相關工藝[2-3],已經成為當前微型高精度陀螺研究的熱點[4]。但半球陀螺的研究主要集中在美國、俄羅斯和英國等幾個國家。我國對半球陀螺的研究起步較晚,雖在理論及實驗等方面取得了一定的成功,但距離世界先進水平仍有較大的差距,且國內研究成果主要是傳統半球陀螺,對于微機械半球陀螺的研究較少[5-6]。現研究階段由于陀螺受檢測模態位移影響,陀螺的輸出誤差增大,并導致陀螺固有性能的漂移,限制了陀螺的動態性能。因此,從控制系統分析出發,尋找解決檢測模態對陀螺性能影響的方法,對于微機械半球陀螺的發展具有一定的意義。

硅基環形波動陀螺作為MHRG的一種,其結構中存在的原理性不利因素導致環形陀螺模態頻差普遍較小,而小頻差的特性會嚴重限制陀螺的動態性能[7,8]。另外,檢測模態作為陀螺科里奧利信號的敏感機構,其位移直接影響陀螺的測量結果[9],而復雜的應用環境和陀螺自身的加工及耦合誤差是影響測量穩定性和精度的重要因素[10]。為了減小檢測模態對環形陀螺儀測量精度的影響,提高系統性能,必須采用有效的手段對陀螺的檢測模態位移進行消除[11]。

檢測閉環系統作為一種拓展陀螺檢測系統帶寬、提高陀螺動態性能的方法,具有低成本、結構簡單、易于實現等優點。但由于力平衡工作模式下的檢測閉環系統對控制電路中的V/F轉換力矩器性能要求極為嚴格,所以也存在以下缺點[12]:

1)在力平衡工作模式下,陀螺控制電路中的V/F轉換力矩器會隨磁場變化產生感生電動勢,從而引起控制電路的閉環輸出標度因數非線性偏差。

2)力矩器的工作點變化較大,因此對力矩器的標度因數要求嚴格,其非線性誤差將影響到系統的測量精度。

3)輸入速率大范圍變化會引起力矩器功率大范圍變化,導致陀螺內部熱不穩定,使其與溫度有關的誤差增大,需要增加一定的溫度補償措施。

目前比較成熟的檢測閉環控制方案有中國電子科技集團公司第十三研究所設計的機電結合帶通Sigma-Delta閉環檢測系統[13];蘇州大學提出的一種基于虛擬科氏力相位特性的自動模態匹配閉環控制方法[14]。但這兩種方案應用條件苛刻,需要對頻差和檢測模態品質因數精確匹配,致使其通用性差,只能針對單個硅微陀螺儀設計,無法滿足大批量陀螺快速生產的需要。

綜上所述,檢測閉環控制系統可以使陀螺在窄頻差狀態下擁有高機械靈敏度、高信噪比、高線性度等優良靜態性能的同時具備大帶寬等動態特性[15],是窄頻差硅基環形波動陀螺必不可少的一種控制方式。但在力平衡工作模式下的檢測閉環系統對力矩器性能要求極高,本文采用的差分電容式驅動方式可以有效提高力矩器的線性度和驅動效率,極大地降低該控制系統中力矩器對陀螺輸出的影響。此外,現有的閉環控制方案都有應用條件苛刻、通用性差的問題。本文提出的一種基于PID-IE的串聯相位超前校正檢測閉環控制系統,可以滿足大批量硅基環形波動陀螺閉環控制器的通用性要求。本文通過對窄頻差U形彈性梁硅基環形波動陀螺儀結構的理論力學等效模型分析建立了該陀螺的動力學方程,并將其與陀螺檢測模態的外圍電路相結合,建立了該陀螺的檢測模態理論模型。本文通過對該模型的開環傳遞函數分析,設計出了一種基于PID-IE的串聯相位超前校正檢測閉環控制器。將該控制器加入陀螺檢測模態反饋回路后,通過對檢測閉環系統傳遞函數波特圖及奈奎斯特圖判穩,驗證了該檢測閉環控制系統的可行性。通過對該陀螺的檢測閉環控制系統在時域上進行仿真后發現,該系統極大提高了環形陀螺的系統穩定時間。這些相關技術的研究對提高MEMS環形陀螺儀的性能具有重大作用,為后續深入研究奠定了基礎。

1 硅基環形波動陀螺結構及控制原理

1.1 陀螺結構模型的建立及其工作原理

本文采用的窄頻差硅基環形波動陀螺的結構如圖1所示,主要由環形諧振子、圍繞環形諧振子的24個控制電極以及U型梁構成。周圍的24個電極每3個一組構成8組差分電極,主要用于環形諧振子的控制與調諧。其中驅動軸有兩組驅動電極和兩組驅動檢測電極,配合外圍電路構成陀螺的驅動閉環回路,檢測軸兩組檢測電極用于采集陀螺輸出,兩組檢測反饋電極用于加入陀螺的正交反饋力和檢測閉環反饋力。該結構采用全對稱的U形彈性支撐梁,不僅具有受殘余應力影響小、頻差窄的特點,而且采用的差分電容驅動方式還使其具有高靈敏度的特點[16]。

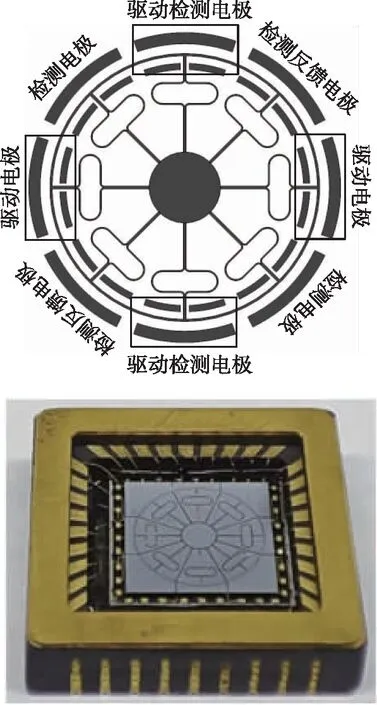
圖1 環形陀螺結構示意及實物圖Fig.1 Structure and physical diagram of ring gyro

通過對窄頻差硅基環形波動陀螺進行力學分析,建立其機械結構模型如圖2所示,結構中包含8個“彈簧-阻尼-質量塊”二階系統。其中0°和90°方向的梁為驅動等效梁,45°和135°方向的梁為檢測等效梁[17]。

圖2 陀螺理論等效模型Fig.2 Equivalent model of gyro theory

根據振動力學原理,該環形陀螺的動力學方程式如式(1)所示[18]。

(1)

式中,x、mx、cx、kx和y、my、cy、ky分別為驅動模態和檢測模態的位移、等效諧振質量、等效阻尼系數和等效剛度系數;λ為科氏耦合系數,Fx為驅動模態施加的靜電力,Fy為檢測模態的檢測反饋力,Ωz為垂直于環形陀螺平面的角速度輸入。當環形諧振陀螺為開環工作模式時,Fy=0。設驅動靜電力Fx=Fdsin(wdt),Fd為驅動靜電力幅值,則驅動模態的位移為[19]

(2)

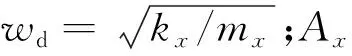
=Aysin(wdt+φy)

(3)

式中,Qy、wy分別為陀螺檢測模態的品質因數和諧振頻率;Ay為檢測位移幅值;φy為陀螺檢測模態相角偏移。

(4)

通過以上推導可知,檢測模態輸出中的科氏信號與驅動靜電力Fx同頻同相,而驅動靜電力與驅動回路中驅動電壓同頻同相;又由于正交信號是驅動模態耦合信號,所以檢測模態輸出中的正交信號與驅動模態檢測電壓同頻同相,所以本文采用了模擬開關相敏解調的信號提取方案。由于已知驅動靜電力Fx=Fdsin(wdt),可設驅動電壓為Vd=Vdxsin(wdt),式中Vdx為驅動電壓幅值,則驅動檢測電壓可設為Vds=Vaxcos(wdt),式中Vax為驅動檢測電壓幅值。本文采用的陀螺控制電路主要由驅動閉環控制、正交閉環控制和檢測閉環控制電路三部分組成,陀螺整體控制電路框圖如圖3所示。

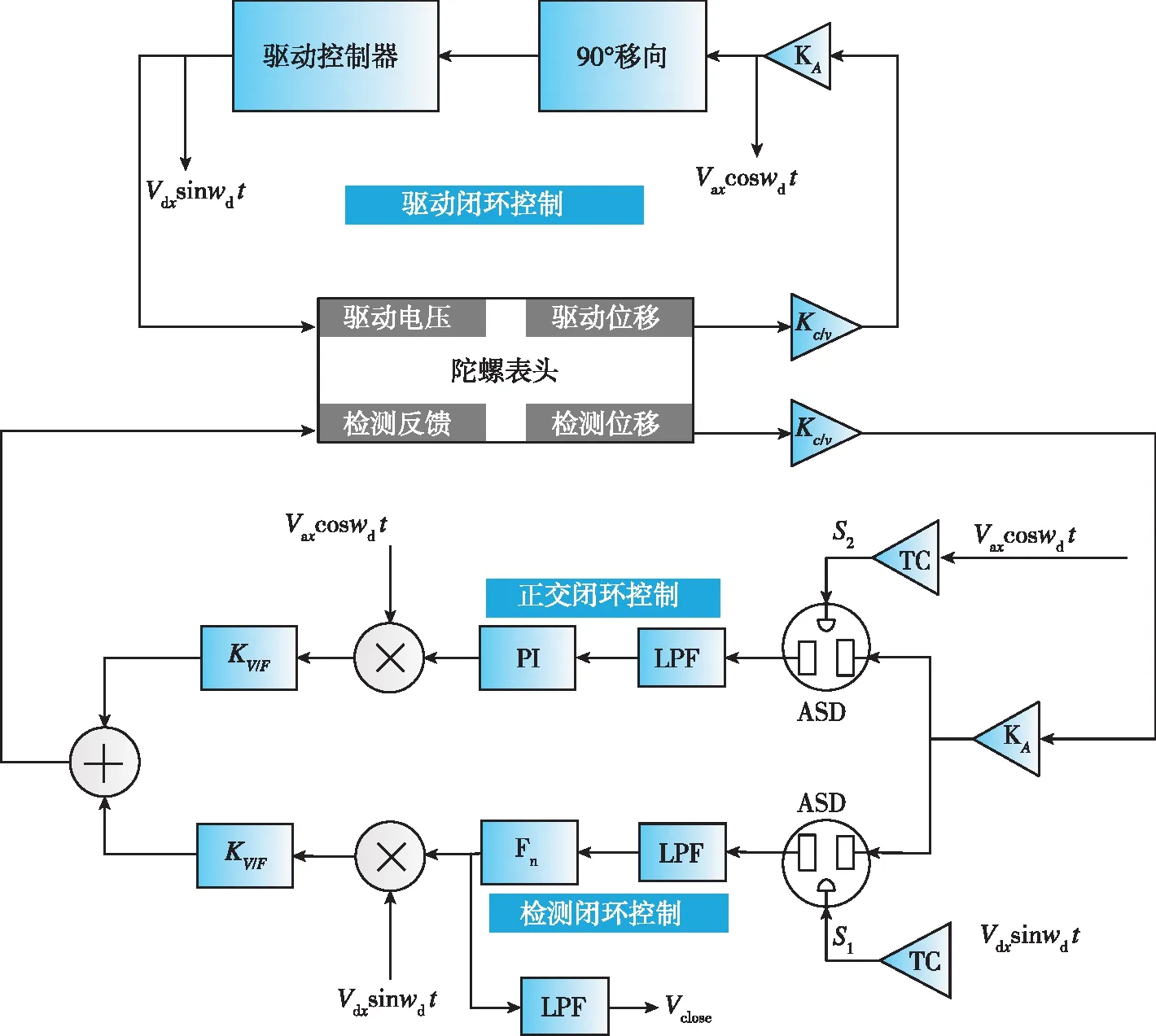
圖3 陀螺控制電路框圖Fig.3 Gyro control circuit diagram

圖中,Kc/v為電容-電壓轉換系數;KA為陀螺前端儀表放大器放大系數;TC為閾值比較器(thres-hold comparator, TC);ASD為模擬開關解調器(analog switch demodulation, ASD);LPF為低通濾波器(low-pass filter, LPF);S1、S2分別為科氏信號和正交信號的解調方波信號;PI為正交閉環控制器;Fn為檢測閉環控制器;KV/F為電壓反饋力轉換系數;Vclose為檢測閉環輸出。在該控制系統中,通過驅動控制器對驅動檢測信號進行自動增益控制(automatic gain control, AGC),實現了該控制系統的驅動閉環控制,驅動閉環回路中的驅動電壓和驅動檢測電壓分別為檢測閉環電路和正交閉環電路提供調制與解調的基準,實現了檢測信號中正交信號和科氏信號的提取,為檢測閉環和正交閉環的實現提供了基本條件。

1.2 陀螺閉環檢測工作原理

本文的檢測閉環系統采用了基于PID-IE的模擬開關相敏解調控制方案。通過驅動回路中的驅動電壓Vd的相位和頻率作為解調基準提取陀螺檢測模態輸出中的科氏信號,并通過基于PID-IE的控制器實現了該陀螺的檢測閉環控制。本文采用的檢測閉環系統框圖如圖4所示。

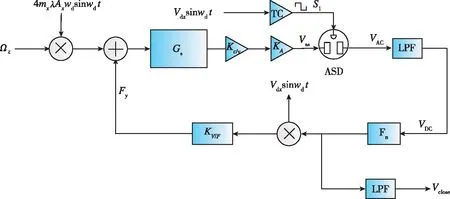
圖4 陀螺檢測閉環系統框圖Fig.4 Gyro detection closed-loop system block diagram

圖中,Gs為環形陀螺檢測模態傳遞函數;Vss為檢測電壓輸出;VAC為解調交流電壓輸出;VDC為檢測開環電壓輸出。陀螺的檢測模態上的檢測位移信號通過Kc/v后,電容信號轉換為電壓信號,然后通過前端儀表放大KA得到陀螺檢測電壓輸出信號Vss。

由陀螺的工作原理可知,在陀螺正常工作狀態下,檢測模態受到科氏力和正交力兩種作用力,則檢測輸出信號Vss包含科氏信號與正交信號。則檢測輸出信號Vss可表示為式(5)。

Vss=Aqcos(wdt)+Acsin(wdt)

(5)

式中Vq為正交信號幅值,Vc為科氏信號幅值。

要從檢測輸出信號Vss中提取出科氏信號,則需要驅動電壓Vd作為相敏解調的基準信號。而本文采用的解調方式為模擬開關相敏解調,其中模擬開關ASD需要的解調基準為數字信號,所以需要對驅動電壓信號Vd進行數字化處理。本文采用閾值比較器TC,Vd經過處理后轉變為方波信號S1。

(6)

式中,k為整數,T為驅動電壓信號的周期。1和-1為數字信號,表示輸入的邏輯關系。當模擬開關ASD的邏輯輸入為1時,模擬開關輸出為原信號,當模擬開關ASD的邏輯輸入為-1時,模擬開關輸出為原信號的反向信號。則科氏信號解調輸出的VAC可表示為

VAC=ASD(Vss)

=Aqcos(wdt)+Acsin(wdt),

(7)

解調之后的信號VAC中,由驅動模態的耦合到檢測模態的正交信號為Aqcos(wdt)在區間[0,π]的周期信號;由科氏力引起的科氏信號為Acsin(wdt)在區間[0,π]的周期信號。則VAC通過低通濾波器LPF得到檢測開環輸出信號VDC推導如式(8)。

VDC=LPF(VAC)

(8)

環形陀螺工作在開環模式下時,通過解調得到的直流科氏信號VDC就可以作為反映陀螺角速率的開環輸出。當環形陀螺工作在閉環工作模式下時,直流科氏信號VDC通過檢測閉環控制器Fn輸出反饋控制電壓,反饋控制電壓再由驅動模態的驅動靜電力Vd調制后反饋回檢測模態。檢測模態的科氏位移響應在檢測反饋力Fy的作用下基本趨于零,此時陀螺輸入角速率Ωz與檢測模態的檢測反饋力Fy的關系為

(9)

因此,陀螺輸入的角速度信息可以通過檢測閉環控制器輸出的控制電壓經過低通后的檢測閉環輸出Vclose得到。

1.3 正交信號抑制原理

由于本文采用的檢測閉環控制方案為相敏解調,但正交誤差的存在會導致陀螺驅動模態信號耦合到檢測模態,這會嚴重影響檢測閉環系統的解調精度,所以可以認為正交閉環控制是檢測閉環系統實現的基礎。由于正交信號是驅動模態耦合信號,所以檢測模態輸出中的正交信號與驅動模態檢測信號同頻同相。則可用驅動檢測電壓Vds的相位和頻率作為解調基準提取陀螺檢測模態輸出中的正交信號,本文采用的模擬開關相敏解調正交閉環系統框圖如圖5所示。

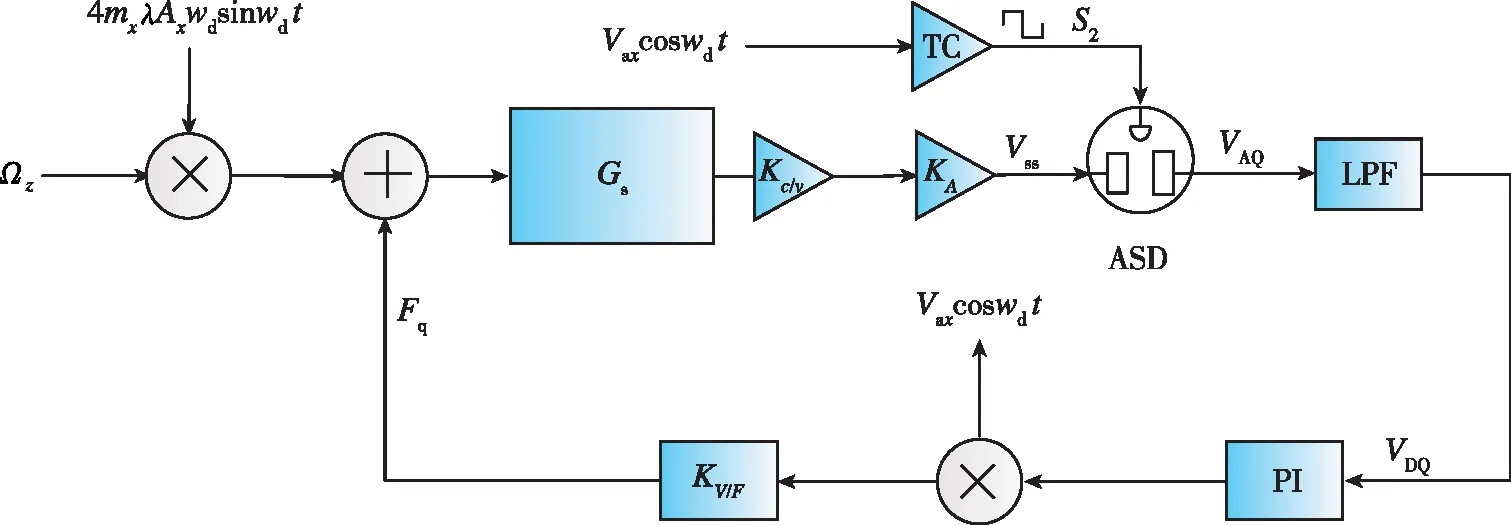
圖5 陀螺正交閉環系統框圖Fig.5 Gyro quadrature closed-loop system block diagram

圖中,VAQ為解調正交信號交流輸出;VDQ為正交直流輸出;Fq為正交反饋力。

由1.2節可知,檢測輸出信號Vss可表示為式(5),要從檢測輸出信號Vss中提取出正交信號,則需要驅動檢測電壓Vds作為相敏解調的基準信號,對檢測輸出信號進行解調。本文采用的是模擬開關解調,所以需要對解調基準信號驅動檢測信號Vds進行數字化處理,通過閾值比較器TC數字化處理后,驅動檢測信號Vds轉變為方波信號S2。

S2=TC(Vd)

(10)

式(10)中相關參數均已在1.2節中說明。該方波信號主要用于模擬開關ADS的解調開關信號,檢測輸出信號Vss在模擬開關ASD的作用下,經過方波信號S2解調后得到的正交交流信號解調輸出VAQ可表示為

VAQ=ASD(Vss)

=Aqcos(wdt)+Acsin(wdt),

(11)

解調之后的信號VAQ中,由驅動模態的耦合到檢測模態的正交信號為Aqcos(wdt)在區間[-π/2,π/2]的周期信號;由科氏力引起的科氏信號為Acsin(wdt)在區間[-π/2,π/2]的周期信號。則VAQ通過低通濾波器LPF得到正交直流輸出信號VDQ推導如式(12)。

VDQ=LPF(VAC)

(12)

當環形陀螺實現正交閉環后,直流正交信號VDQ通過正交閉環控制器PI控制器輸出正交反饋控制電壓,反饋控制電壓再由驅動模態的驅動檢測信號Vds調制后反饋回檢測模態。檢測模態的正交誤差信號在正交反饋力Fq的作用下基本趨于零,此時就實現了檢測模態的正交閉環控制。

2 PID-IE檢測閉環控制系統設計

為了實現環形陀螺的檢測閉環控制,檢測閉環控制器的設計需要對檢測模態開環傳遞函數進行分析。通過1.2節中的檢測閉環回路框圖(圖4),可以得到該環形陀螺的檢測開環傳遞函數Gc為

Gc(s)=AxwdVdxKc/vKALPF(S)Gs(s)

(13)

式中,Gs為環形陀螺檢測模態陀螺模型的等效傳遞函數,表達式如下

Gs(s)=

(14)

通過實驗測試,該環形陀螺的基本參數如表1。

表1 環形陀螺參數匯總Table 1 Summary of ring gyro parameters

根據測試參數可以看出,該陀螺的驅動模態與檢測模態品質因數相差較大,主要是由陀螺加工誤差所致。從原理上來說,陀螺的品質因數只與陀螺該模態的等效質量、等效剛度以及等效阻尼有關,環形陀螺作為全對稱的結構,陀螺驅動與檢測模態的品質因數應該基本一致。但由于加工誤差會導致其兩個模態的等效質量與等效剛度出現一定誤差,而該陀螺采用的高真空高度封裝會導致其等效阻尼極小,這種情況會放大等效質量與剛度的誤差對陀螺品質因數的影響,進而導致該陀螺兩個模態品質因數相差較大。又由于其對稱結構會導致檢測模態與驅動模態頻差極小,所以當陀螺工作在驅動模態的諧振頻率下時,檢測模態的高品質因數會導致驅動模態耦合到檢測模態的正交信號出現極大的響應,此時檢測模態輸出的正交信號遠大于科氏信號,不利于檢測信號中科氏信號的提取,所以我們一般選擇品質因數較低的工作模態作為陀螺的檢測模態,這樣更有利于陀螺檢測閉環的實現。通過表1測試的陀螺參數結合該陀螺的傳遞函數,可以得到該陀螺在檢測模態開環工作狀態下的波特圖,如圖6所示。

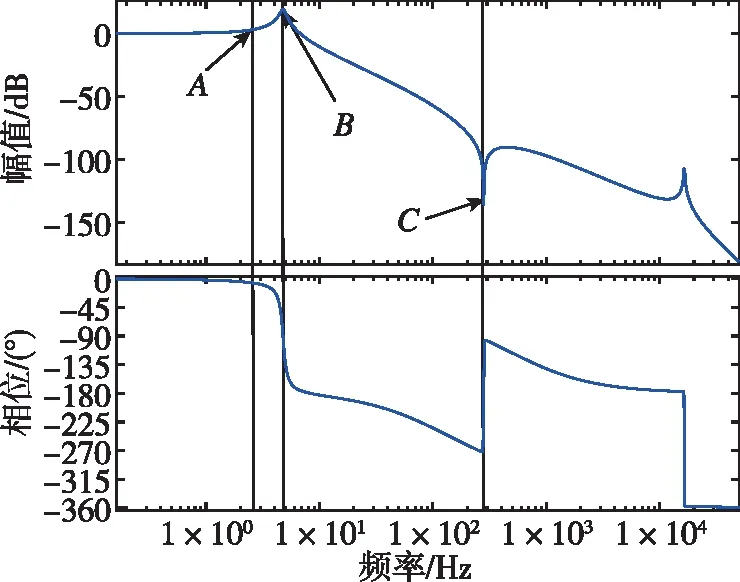
圖6 環形陀螺檢測開環波特圖Fig.6 Ring gyroscope detection open-loop bode diagram

根據閉環回路穩定性原理,開環回路需要有足夠的幅值和相位裕度才可以保證閉環的穩定性。通常情況下相位裕度PM應在30°～60°,幅值裕度GM應大于6 dB。將傳遞函數和圖6結合分析可知,點B諧振峰是由兩個共軛極點造成的,頻率為4.83 Hz,表征陀螺的頻差,其附近會有180°的相位滯后(每個極點相位滯后90°);同時,環形陀螺檢測模態較高的品質因數會導致相位變化較為劇烈。點A為陀螺的帶寬點,陀螺工作在力平衡模式下時,陀螺的帶寬表征的是其檢測系統中增益的穩定性。一般環形陀螺以直流點增益為基準,在帶內波動超出±3 dB,則表示其超出帶寬,該點即為陀螺的帶寬點。在理論計算中,環形陀螺的帶寬點為其檢測模態與驅動模態頻差的0.54倍[20],圖6中該點頻率為2.65 Hz,與實際測試出的模態頻差Δw的0.54倍基本一致。點C為陀螺的兩個共軛零點,其附近會有180°的相位超前。所以,必須對相位和幅值進行校正和補償,保證系統有足夠的相位和幅值裕度。

PID-IE閉環控制器的設計目標是在保證系統有足夠幅值和相角裕度的前提下提高系統的帶寬。此外,由檢測閉環回路框圖(圖4)可知,系統帶寬和穩定性只與中間的閉環回路有關,該閉環回路可表達為單位負反饋系統,該系統的開環傳遞函數P可表達為

P(s)=VdxKV/FVdxKc/vKALPF(s)Fn(s)Gs(s)

(15)

將式(15)和式(13)比較可知,除反饋控制器Fn外,式(15)其余部分的頻率特性可參照檢測開環狀態的系統波特圖(圖6)。通常情況下,系統開環特性低頻段的增益應滿足穩態誤差的要求,中頻段剪切點(經過0 dB線)的斜率應為-20 dB/dec,高頻段增益應盡可能迅速衰減以減小高頻噪聲對系統的影響。同時,相位超前校正裝置可以增大系統的相角裕度,降低系統響應的超調量,也可增大系統帶寬,加快系統的響應速度。根據上述分析,Fn在低頻段采用PID控制器中的積分環節以最大限度減小穩態誤差;在中頻段,由于在頻差點B附近有180°的相位滯后,且變化劇烈,嚴重影響了相角裕度,所以在B點之前必須采用PID中的微分環節補償相位,則經過B點之后斜率即為-20 dB/dec。在高頻段,經過點C后斜率又回到-20 dB/dec,后在二階低通濾波器LPF影響下斜率變為-60 dB/dec,已可以滿足衰減高頻噪聲的需求,但為了匹配中頻段的微分環節,應在高頻段加入慣性環節IE,此時在高頻段斜率為-80 dB/dec,可以很好地衰減高頻噪聲,則控制器Fn的傳遞函數為

(16)

式中,k為該傳遞函數的比例系數,k=24;τ1為控制器中的微分和積分環節的參數,τ1=(0.33·2π)-1;τ2為控制器中的慣性環節的參數,τ2=(400·2π)-1。

通過上述分析,閉環控制器電路采用兩級串聯校正控制的方法,第一級為PID環節,其主要作用是對低頻段進行穩態增益補償并校正中頻段的180°相位滯后;第二級為IE環節,其主要作用是補償中頻段微分環節的相位并衰減高頻段噪聲。設計電路結構如圖7所示,其中,電路參數如表2所示,在該電路中第一級的R1=R2=R,C1=C2=C。則電路傳遞函數為

表2 閉環控制器電路參數匯總Table 2 Closed-loop controller circuit parameters summary

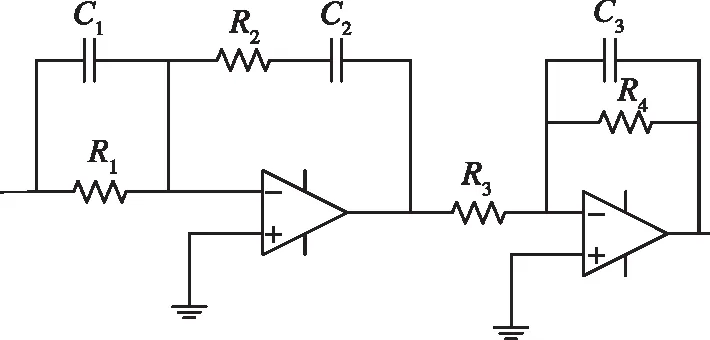
圖7 PID-IE控制器電路Fig.7 PID-IE controller circuit

(17)

根據式(15)并結合檢測閉環控制框圖(圖4),可以得出該陀螺的檢測閉環系統傳遞函數如式(18)所示。

(18)

通過該檢測閉環傳遞函數對該閉環控制系統的穩定性進行分析,可以得到其奈奎斯特曲線,如圖8所示,圖中曲線并未包括(-1,0j)點,可以證明系統是穩定的。檢測閉環系統的開環波特圖和閉環波特圖如圖9和圖10所示,圖9中顯示的最小相位裕度為35°,幅值裕度為11.1 dB,這均滿足前面提及的指標。從圖10可以看出加入控制器后,帶內最高拐點為-12.8 dB,未超過直流時-13.9 dB的±3 dB范圍,系統的帶寬為109 Hz,達到了拓展帶寬的目的。

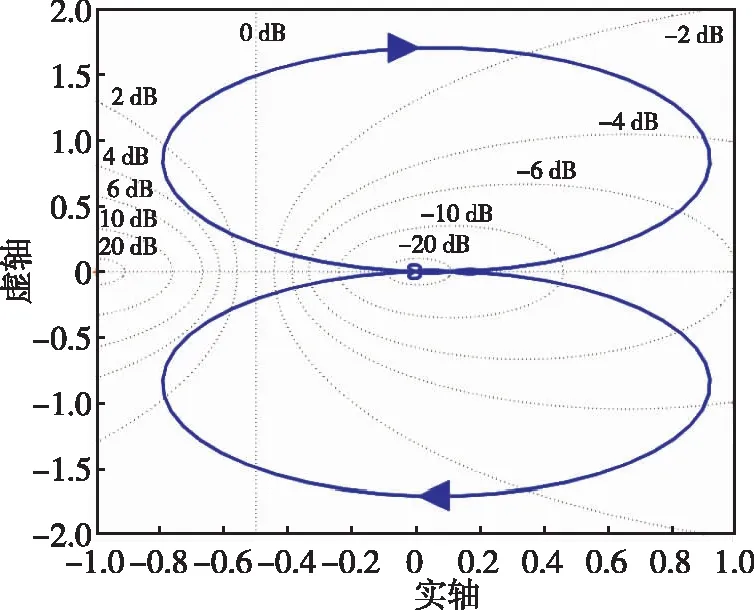
圖8 檢測閉環控制系統奈奎斯特圖Fig.8 Nyquist diagram of detection closed-loop control system

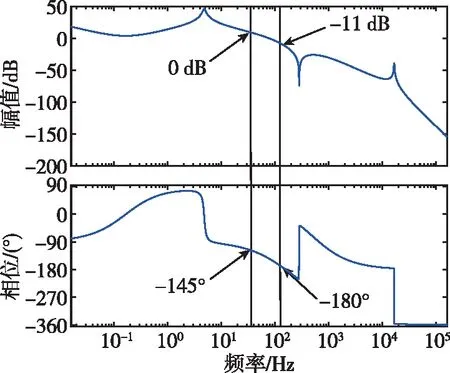
圖9 系統開環波特圖Fig.9 System open-loop Bode diagram

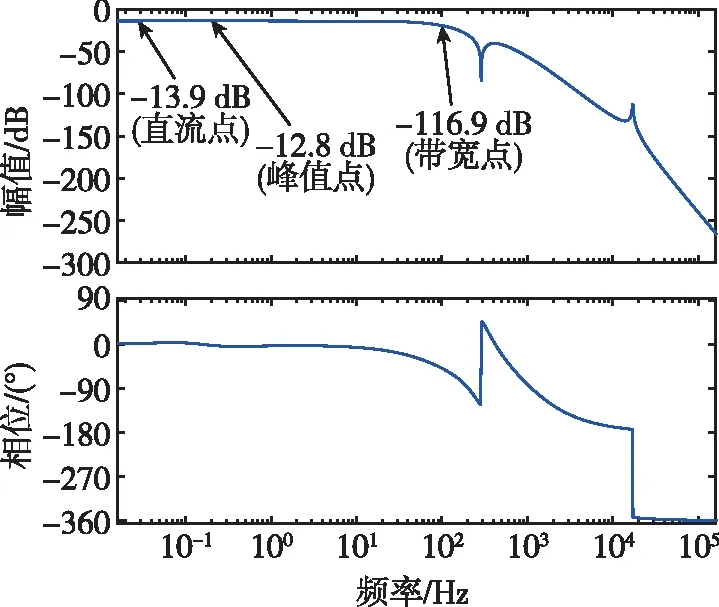
圖10 系統閉環波特圖Fig.10 System closed-loop Bode diagram

3 檢測閉環控制系統仿真

本文以環形陀螺檢測閉環系統的傳遞函數和系統框圖為基礎,建立了檢測模態的檢測閉環系統模型,如圖11所示。并在該模型上分別進行了環形陀螺在檢測開環工作狀態和檢測閉環工作狀態下的時域仿真。

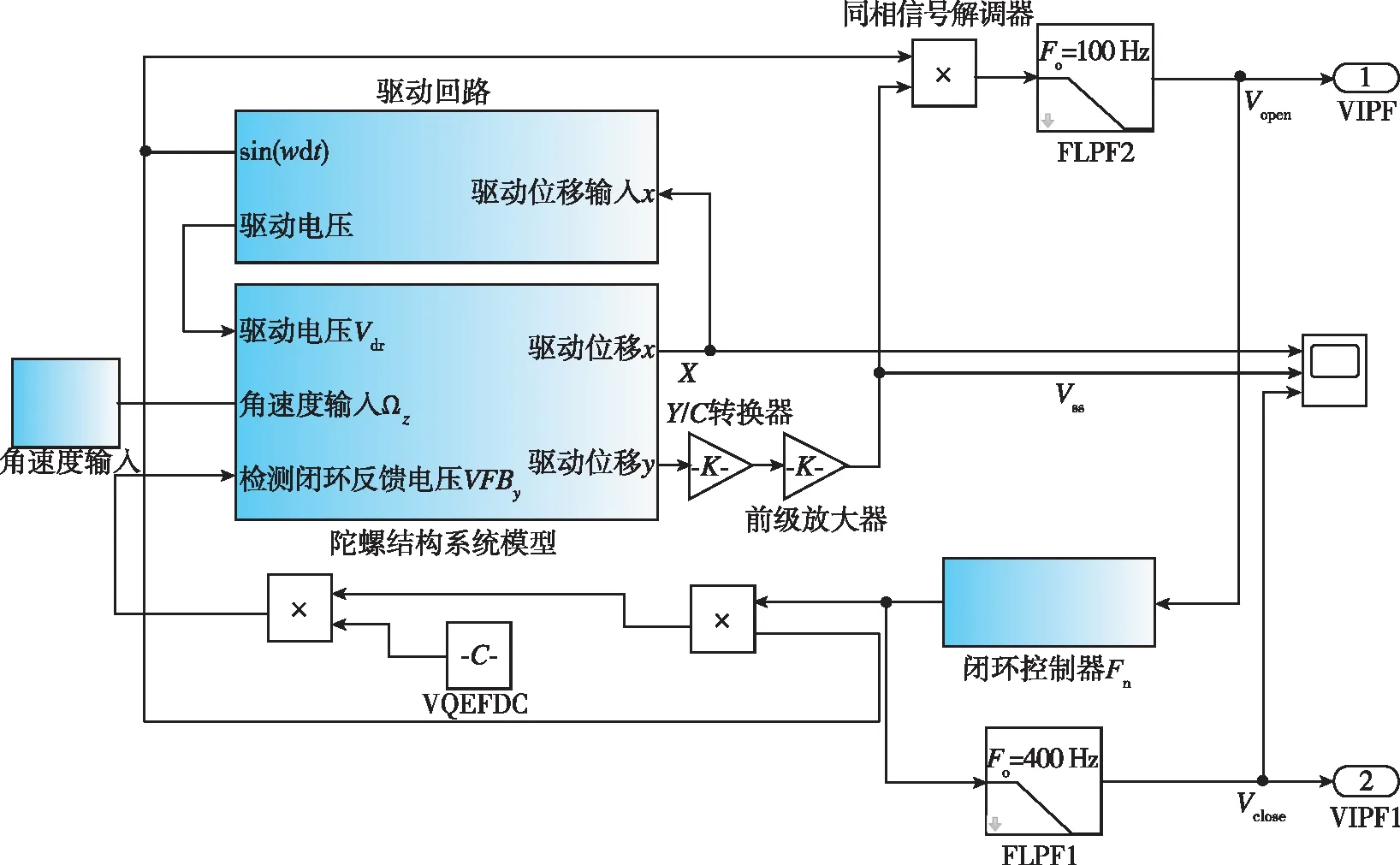
圖11 檢測閉環系統仿真模型Fig.11 Detection closed-loop system simulation model

為了減小其他因素對陀螺的影響,實現環形陀螺在開環和閉環工作狀態的仿真對比。本文在環形陀螺系統仿真開始時(t=0 s),在其他參數完全相同的前提下,分別對陀螺在開環工作狀態和閉環工作狀態下加入Ωz=100(°)/s的階躍信號,之后每過2 s,系統輸入會遞增Ωz=100(°)/s的輸入角速度信號,仿真時間共計為10 s。為了驗證檢測閉環系統的有效性,本文在檢測開環系統中采集了三路信號,如圖12所示,分別為驅動位移x、檢測位移輸出信號Vss和檢測開環輸出信號VDC;在檢測閉環系統中采集了三路信號,如圖13所示,分別為驅動位移x、檢測位移輸出信號Vss和檢測閉環輸出信號Vclose,并對兩組輸出信號進行對比。

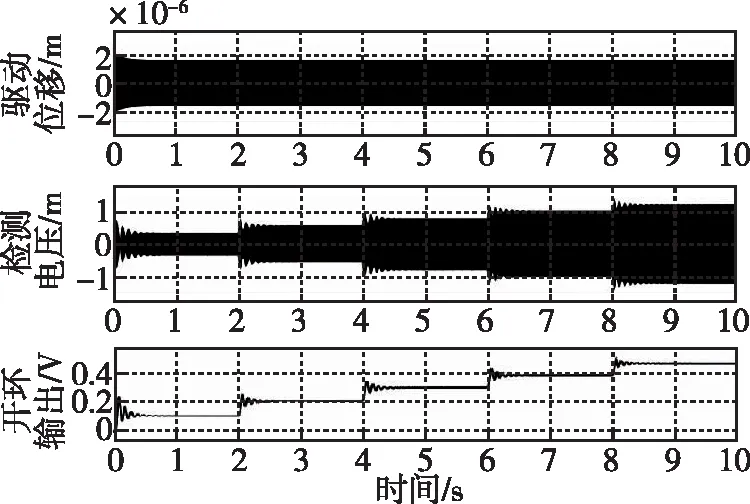
圖12 環形陀螺開環工作狀態仿真Fig.12 Open-loop working state simulation of ring gyroscope

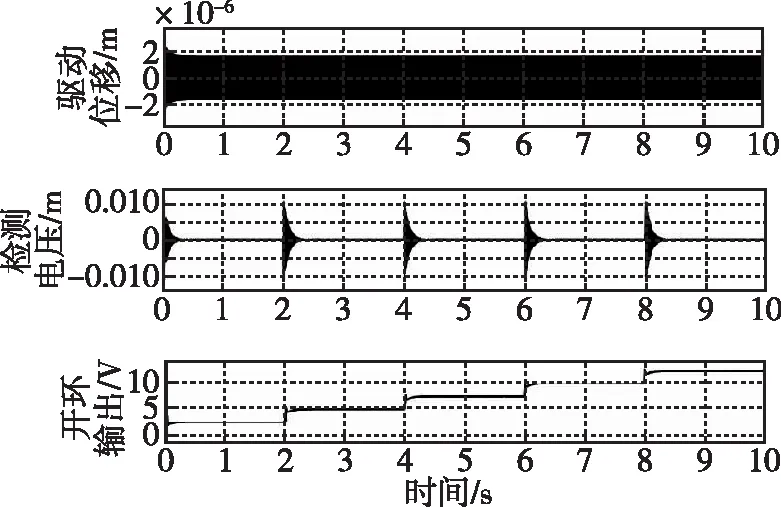
圖13 環形陀螺閉環工作狀態仿真Fig.13 Closed-loop working state simulation of ring gyroscope

圖12中,環形陀螺工作在檢測開環工作狀態下,系統穩定時間約為0.5 s,且陀螺開環輸出有較大的超調。圖13中,環形陀螺工作在檢測閉環工作狀態下,系統穩定時間約為0.2 s,且陀螺閉環輸出超調量極小。兩圖對比可知,在恒定角速率Ωz=100(°)/s輸入時閉環檢測位移輸出信號Vss比開環檢測位移輸出減小了2個數量級,說明檢測反饋力基本可以平衡科氏力對環形陀螺產生的作用。

4 實驗測試

根據設計的檢測閉環控制系統,在模擬電路中實現了該控制系統的硬件電路并搭建了完整的測控系統,用于測試檢測閉環前后陀螺的各項性能指標。

為了驗證該檢測閉環控制系統的有效性,首先測試了該檢測閉環系統在轉臺勻速轉動的狀態下,該控制系統從檢測開環工作狀態轉換為檢測閉環工作狀態環形陀螺的檢測位移輸出,測試平臺及硬件電路如圖14所示。

圖14 環形陀螺閉環控制電路及測試平臺Fig.14 Closed-loop control circuit and test platform of ring gyroscope

圖15所示為該環形陀螺在轉臺勻速轉動時,控制系統從開環工作狀態轉換為閉環工作狀態的驅動位移及檢測位移輸出測試結果。由該圖可以看出,環形陀螺在勻速轉動的狀態時,未加入檢測閉環控制的檢測位移信號與驅動位移信號相位相差90°,幅值約為309 mV,因此可以認為該檢測位移信號主要是由陀螺輸入的科氏力引起的;加入檢測閉環控制后,檢測位移幅值變為11.3 mV,檢測位移減小了97%。

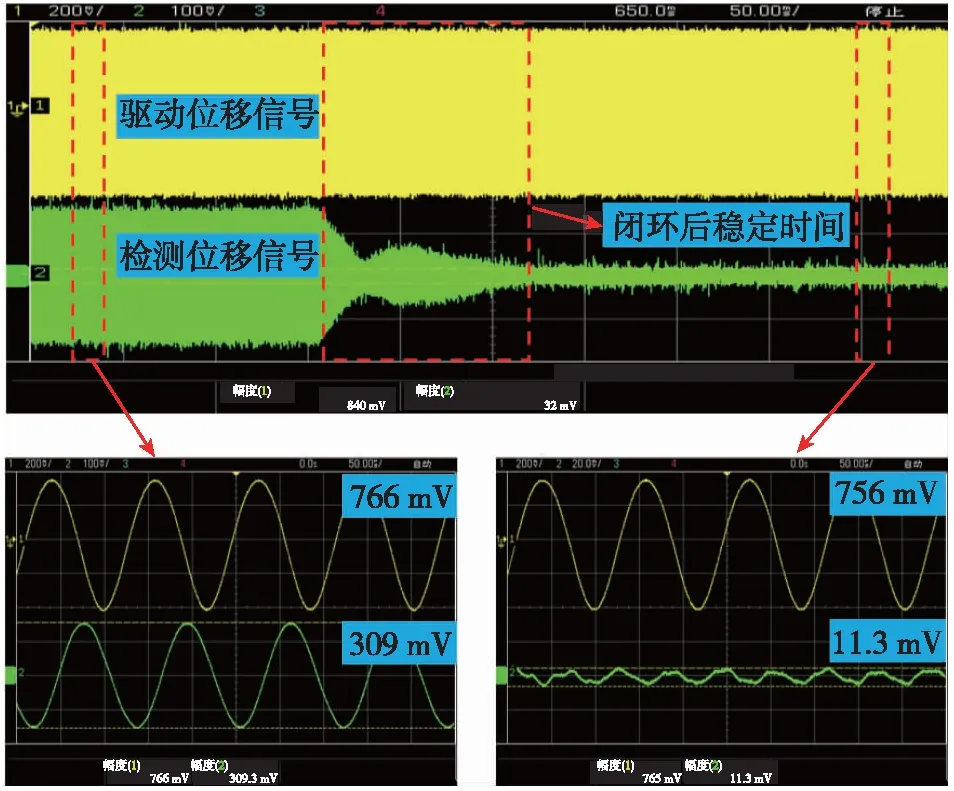
圖15 環形陀螺驅動位移及檢測位移信號輸出Fig.15 Driving displacement and detection displacement signal output of ring gyroscope

但是在加入檢測閉環控制后,檢測位移信號未能完全抑制,其主要原因是環形陀螺的原理性不利因素導致其在物理模型中驅動位移和檢測位移的有效檢測位置為環形諧振子的波節點與波腹點,但在電路實現過程中,驅動和檢測位移是采用電容檢測的方式讀出,因此在陀螺檢測位移點實現完全抑制的情況下,檢測電容會讀出檢測位移點兩側的電容變化,此時檢測電容的輸出為原檢測位移信號的二倍頻,這種情況下也可以認為該陀螺的檢測位移實現了完全抑制。且從圖15中可以看出,在加入檢測閉環控制后,檢測位移的幅值在0.15 s內達到了穩定,與仿真結果0.2 s基本一致。也證明了該控制系統是可行的,能夠有效、穩定地實現檢測位移的消除。

接下來分別對環形陀螺檢測閉環前后各項性能指標進行對比測試,首先通過圖14所示速率轉臺對環形陀螺進行標度因數測試,將被測陀螺水平放置在小型單軸轉臺上,接通電源并預熱30 min,正常工作后控制轉臺分別以±1(°)/s、±2(°)/s、±5(°)/s、±10(°)/s、±50(°)/s、±100(°)/s、±150(°)/s進行轉動,采用示波器測試轉動過程中環形陀螺的輸出電壓并進行記錄。重復測試開環和閉環輸出數據后對其進行線性擬合,最終測試結果如圖16所示,圖16(a)為檢測開環標度因數擬合直線,圖16(b)為檢測閉環標度因數擬合直線。

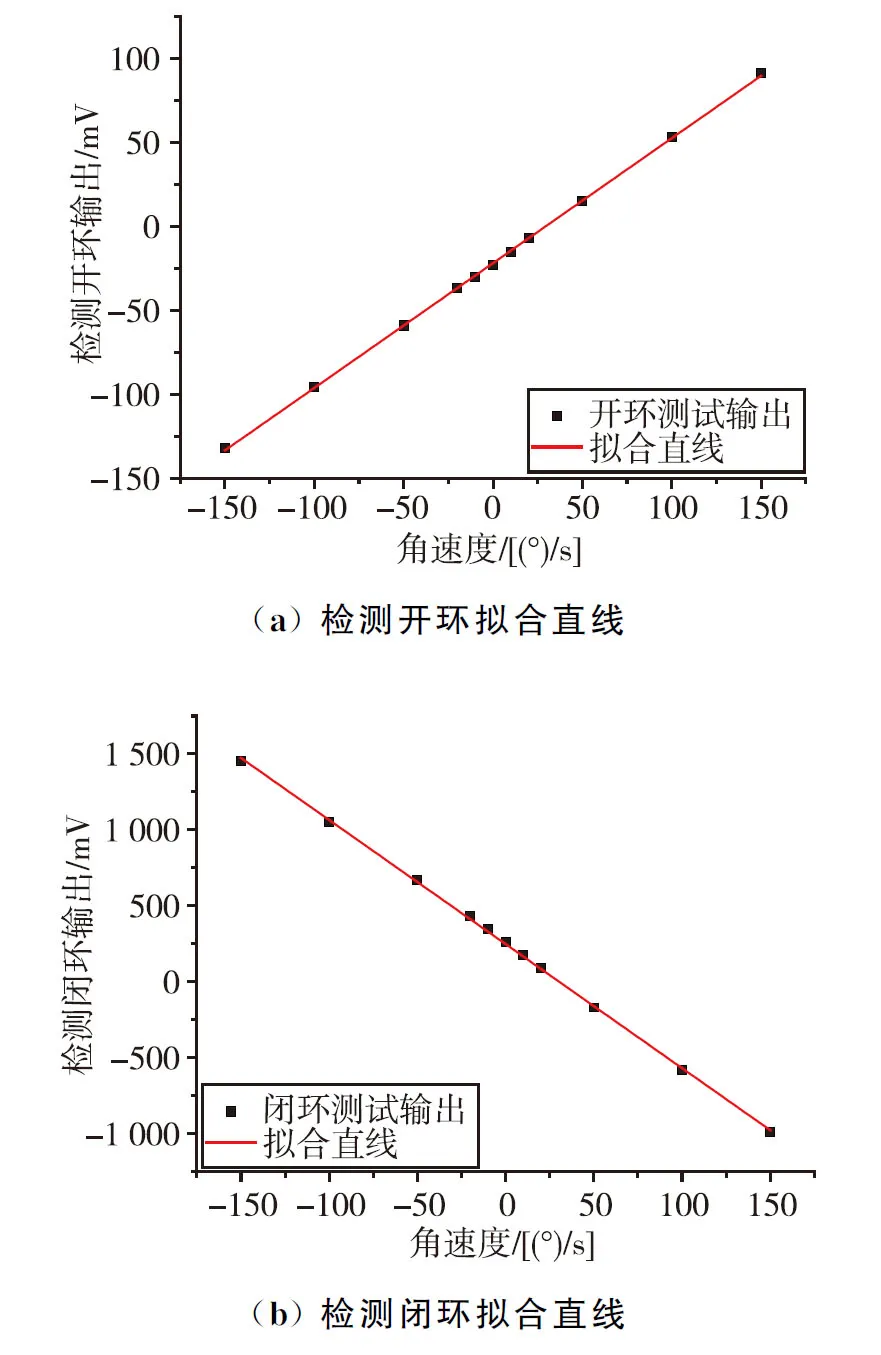
圖16 檢測閉環前后標度因數對比Fig.16 Comparison of scale factor before and after detection closed-loop

然后,對環形陀螺進行靜態零位輸出測試,將被測陀螺放入干擾屏蔽箱內,接通電源并預熱30 min,正常工作后采用多通道數據采集器記錄陀螺零位輸出(采樣周期為1 s,取1 200 s有效數據),測試現場如圖17(a)所示。

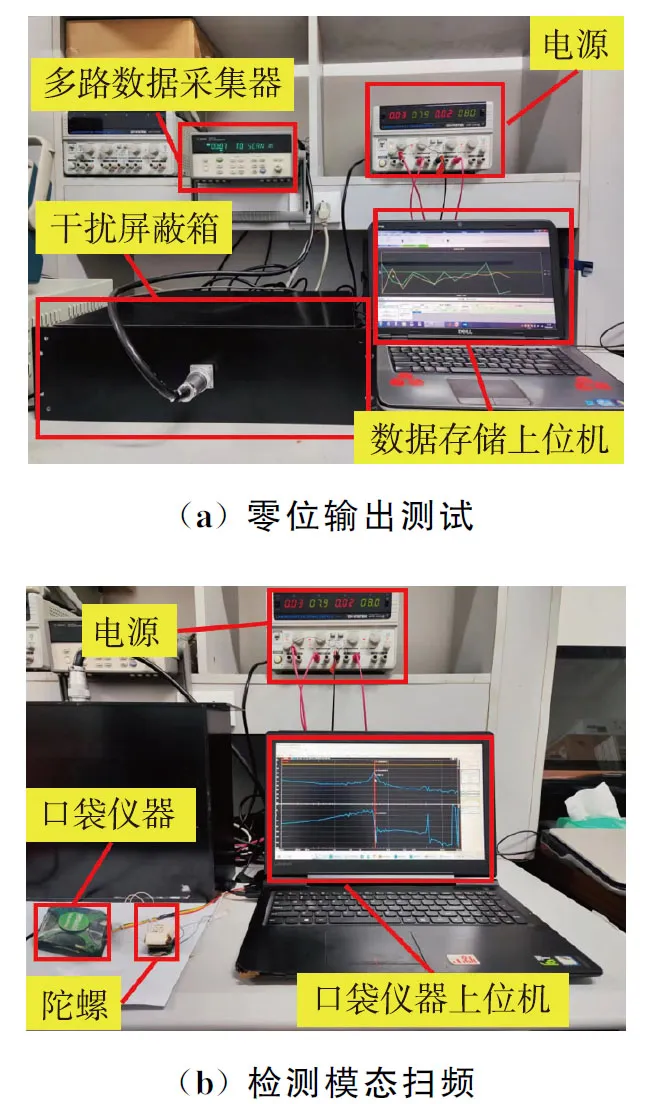
圖17 陀螺測試Fig.17 Gyroscope test

接下來對環形陀螺進行動態檢測模態掃頻測試,本次測試采用的口袋儀器集成了信號發生器和網絡分析儀等,本文將陀螺檢測模態的輸入和輸出作為系統網絡的輸入、輸出接口,通過口袋儀器的網絡分析功能測試陀螺檢測模態的波特圖。測試過程如下:將被測陀螺的檢測反饋端和檢測輸出端分別連接口袋儀器的信號輸入和輸出接口,同樣接通電源并預熱30 min,正常工作后通過口袋儀器分別對陀螺檢測模態開環工作狀態和閉環工作狀態進行掃頻測試(掃頻范圍為0.1～1 000 Hz,掃頻測試點200個),測試現場如圖17(b)所示。

通過圖16所示擬合直線可以得到環形陀螺檢測閉環前后的標度因數,結合測試的零位輸出數據,我們可以繪制出環形陀螺檢測閉環前后的零位輸出以及Allan方差曲線,如圖18所示。通過檢測模態掃頻可以分別得到環陀螺檢測開環和檢測閉環的掃頻圖,如圖19所示。以上測試結果匯總見表3。

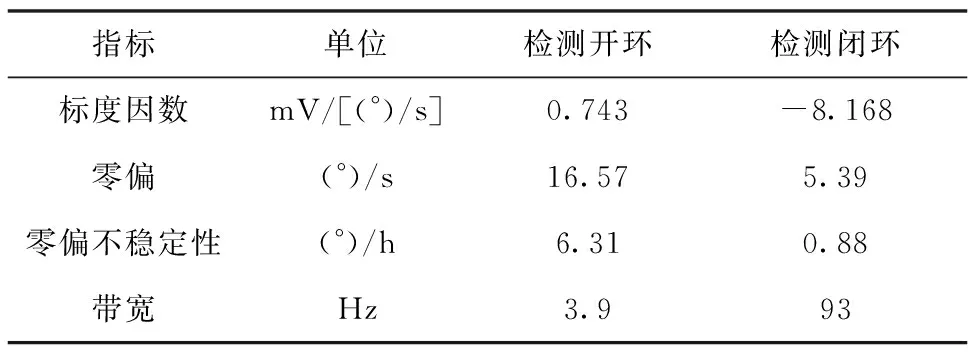
表3 測試結果匯總 Table 3 Summary of test results

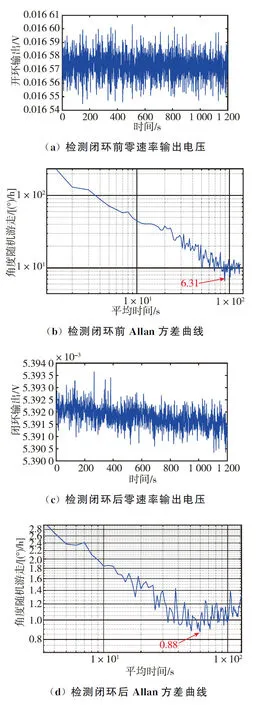
圖18 檢測閉環前后陀螺零速率輸出及Allan方差曲線對比Fig.18 Comparison of zero output and Allan variance curve before and after closed-loop detection

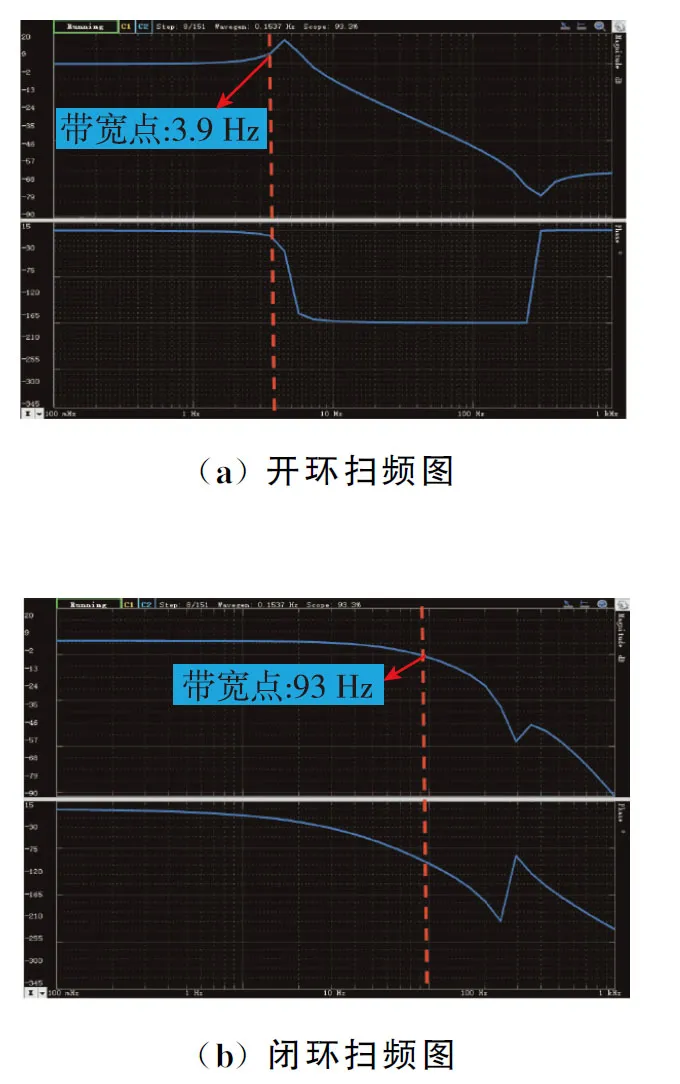
圖19 檢測模態閉環前后掃頻圖Fig.19 Frequency sweep diagram before and after detection mode closed-loop

根據表3測試結果可知,標度因數在環形陀螺實現檢測閉環后提升了10倍,主要原因是檢測開環時,陀螺的標度因數由檢測位移決定,實現檢測閉環后,陀螺標度因數由檢測反饋力決定,而檢測反饋力的輸入電壓遠大于檢測位移輸出電壓。陀螺的零偏及零偏不穩定性在實現檢測閉環后分別為5.39(°)/s和0.88(°)/h,與檢測開環相比提升了3倍和8倍,這是由于檢測閉環抑制了檢測位移,減小了檢測模態中檢測位移對陀螺輸出的影響。陀螺的帶寬在實現檢測閉環后為93 Hz,比檢測開環帶寬提高了30倍。以上測試結果均符合理論分析,且與仿真結果基本一致,驗證了該檢測閉環系統能夠有效抑制檢測位移、提高環形陀螺帶寬,從而大幅提升環形陀螺的性能。

5 結論

本文針對硅基環形波動陀螺窄頻差導致的其帶寬較小、動態性能差和檢測位移大等問題,通過對該陀螺物理模型進行建模并仿真,設計了一種檢測閉環控制系統;在進行實驗測試后,發現該系統實現了環形陀螺的帶寬拓展和檢測位移消除,大幅提升了環形陀螺性能。本文的主要內容如下所述:

1)設計了一種基于PID-IE的串聯校正檢測閉環控制系統,可以實現對環形陀螺帶寬的有效拓展和檢測位移的消除。

2)搭建了環形陀螺的檢測模態系統模型,能夠有效地對該陀螺檢測模態進行仿真。仿真結果表明,相較于開環工作狀態,該陀螺實現閉環檢測后輸出穩定時間減少了50%,且檢測反饋電壓可以很好地抑制檢測位移。

3)搭建了該檢測閉環系統的控制電路及實驗測試平臺。通過實驗測試環形陀螺檢測閉環前后的各項性能指標并進行對比,驗證了該檢測閉環系統可以有效提高環形陀螺的各項性能指標。

本文中的檢測閉環控制系統,通過模擬電路對陀螺檢測系統的相位幅值進行校正和補償,提高了陀螺的動態性能,與傳統檢測閉環控制系統相比,該控制系統采用了一種全新的基于PID-IE的相敏解調控制器,該控制器適用于大部分窄屏差的硅基環形陀螺,具有一定的普遍性和較好的移植性。但模擬電路的控制器主要由運算放大器組成,其控制參數受環境溫度影響較大,力平衡工作模式下的檢測閉環控制系統輸入速率大范圍變化時會引起力矩器功率大范圍變化,導致陀螺內部熱不穩定,使其與溫度有關的誤差增大,需要增加一定的溫度補償措施,否則不能實現高精度控制。今后的工作重點是將該控制系統移植到數字電路,或者在控制系統中加入溫度補償控制,以減小溫度對控制系統的影響,進一步提高該閉環控制系統的控制精度。