航空集群一發多收有源定位最優構型
王維佳,王玉冰,田瑾,毛昭軍,杜琳琳
(1.軍事科學院 系統工程研究院,北京 100020;2.93236部隊,北京 100085;3.武警工程大學,陜西 西安 710086)
0 引言
面對現代戰場環境的高動態、深度不確定性特點,依托航空集群平臺執行定位跟蹤任務能夠獲得更廣的觀測范圍、更高的定位精度以及魯棒性,從而大幅提升戰場態勢感知能力[1]。因此,國內外學者均對集群定位做了大量研究,杜晶等[2]研究了基于時差頻差的無人機集群協同定位模型;Dogancay等[3]基于Fisher信息矩陣(FIM)推導了基于到達角(AOA)定位、到達時間差(TDOA)定位對應的最優構型并應用在無人機集群無源定位中;楊俊嶺等[4]在分析了無人機集群AOA定位后,引入演化深度神經網絡進行無人機集群動態航跡規劃;鐘日進等[5]提出集群內測距和對目標測向的協同定位方法,即集群內進行測距提升平臺之間相對測量精度,同時給出基于AOA協同定位求解算法。當前的研究多基于TDOA、AOA、到達信號強度等定位體制進行無源定位,其前提是目標輻射源向外輻射電磁信號,一旦目標進入電磁靜默模式,集群平臺無法獲取目標信息,因而無法進行無源定位跟蹤任務。
本文在借鑒雙多基地組網雷達[6-7]以及外輻射源無源相干定位[8-9]技術的基礎上,提出基于到達時間(TOA)橢圓定位的航空集群一發多收協同定位方法,在無源定位的基礎上增加集群內的己方合作有源發射機,從而實現對電磁靜默目標的定位跟蹤。
航空集群一發多收有源協同定位跟蹤方式如圖1所示,集群內平臺按角色分為發射機和接收機:發射機通常位于戰場的后方,處于較安全范圍,起到主動發射、數據處理與指揮控制中心的作用;多個接收機平臺處于戰場前方,與發射機保持一定距離,主要負責接收從目標反射的回波信息,接收機不主動發射電磁波,隱蔽性好,從而保證平臺的安全性。航空集群有源協同探測在性能上優勢互補、分工協作,充分發揮各自能力,進一步擴大空中的縱深探測范圍,延伸作戰半徑。圖1中xTr為發射機位置,xTr=[xTr,yTr]T,xi為接收機位置,xi=[xi,yi]T,i=1,2,…,M,M為接收機數量,xt為目標位置,xt=[xt,yt]。

圖1 航空集群一發多收有源協同定位跟蹤示意圖Fig.1 Active localization with one transmitter and multiple receivers in aircraft swarm
因此,采用一發多收的協同定位跟蹤可以有效應對目標輻射源關機的情況,同時具備反隱身能力。對于一發多收的航空集群定位系統,各接收站為副站,主要完成對合作信號的偵收、時間信息提取;發射機為主站,需要對各個副站的測量值進行融合處理,解算目標狀態信息,同時依據當前態勢對集群的構型進行優化,并將決策控制指令分發給各個接收機。
與傳統定位方式不同,集群定位性能除了受到定位體制、定位算法的影響外,還受到集群規模、集群構型的較大影響,因此本文從定位構型優化準則出發,主要分為兩個方面開展研究:一是在有源TOA定位體制下,推導不同接收機數目對目標進行定位的最優幾何構型,即得到最優構型的解析解;二是怎樣將得到的最優構型運用到實際的航跡規劃中,從而進一步提升定位跟蹤精度。
1 一發多收TOA定位模型


圖2 一發多收定位跟蹤示意圖Fig.2 Active localization with one transmitter and multiple receivers
i(xt)=τi(xt)+ei
(1)
(2)

i=‖xt-xTr‖+‖xt-xi‖+ni
(3)

=[r1,…,rM]T+[n1,…,nM]T
(4)
假設n=[n1,…,nM],對應的誤差協方差矩陣為
(5)
2 一發多收TOA定位最優構型分析
克拉美-羅界(CRLB)表征了估計參數的無偏估計方差的下限,體現出估計問題本身的屬性,與具體的定位或跟蹤算法無關,可以作為定位性能的好壞準則。因此,基于CRLB可以對TOA定位的最優構型進行分析,在具體分析過程中,由于CRLB為矩陣形式,通常采取兩種準則[12]:
1) D優化準則,最大化Fisher矩陣J的行列式:arg max det (J);
2) A優化準則,最小化CRLB矩陣的跡:arg min det (J-1);
本節擬分別采用兩種準則對TOA定位的最優構型進行分析。
2.1 基于D優化準則的一發多收最優構型分析
根據通用矩陣FIM矩陣求解方法,可以得到TOA橢圓定位的FIM矩陣[13]為
(6)

(7)


(8)
由D優化準則對該構型進行分析,此時的優化目標函數取值與方位角θ=[θ1,…,θM]有關,可以表示為

(9)
假設ai=(1+cosθi),可知ai的取值范圍為0 (10) 式中:a=[a1,…,aM]。由冪均值不等式可得 (11) 僅且僅當a1=a2=…=aM時,式(11)的等式成立。對于ai>0,由基本不等式可得 (12) 將式(12)代入式(10),可得 (13) (14) a1=a2=…=aM=3/2,則各個接收機之間的最優角度為 |θi|=π/3 rad (15) 由于目標函數的第2項為f2≥0,因此整個目標函數f(θ)的最大值在f1(a)=f1,max(a)、f2=0處取得,可得: 1) 當M為偶數時,對應的最優定位構型為 (16) (17) 2) 當M為奇數時,無法同時滿足式(16)中 2個條件,因而無法直接得到整個目標函數的最大值。此時,式(10)可以變形為 (18) 對式(18)求θi的偏導數,并使其等于0,可得 (19) 從而可得,取極值的條件為或者{θi,θj}={π/3 rad,-π/3 rad}。當時,顯然f(θ)=0,此時發射機、接收機以及目標成一條直線,對應著最差的定位構型。而當{θi,θj}={π/3 rad,-π/3 rad}時,對于奇數個接收機,目標函數的最大值為 (20) (21) 圖3 基于D優化準則的最優構型示意圖Fig.3 Optimal configuration based on D-optimality criterion 2.1節采用D優化準則對一發多收情況下TOA橢圓定位的構型進行了分析,證明了無論接收機數目為奇數還是偶數,對應的最優構型都和發射機與目標之間連線的夾角為π/3 rad。 本節采用A優化準則進行分析,此時的優化目標函數變為 (22) 假設λ1、λ2分別為式(8)的兩個特征值,其中λ1≥λ2,從而可得CRLB的特征值為 (23) (24) 同樣,假設ai=(1+cosθi),此時式(22)可以化簡為 (25) 對于不等式: (26) 等號成立的條件為 a1=a2=…=aM=a (27) 因此可得: (28) 進一步對式(28)化簡可得,當a=4/3時,不等式右邊取得最大值: (29) 為了滿足式(24),對于偶數個接收機,最優的構型可以表示為 (30) 圖4給出了一發四收情況下,采用TOA橢圓定位的最優構型示意圖,偶數個接收機被分為兩組,與目標連線之間的夾角為θi=±arccos(1/3)·180/π=±70.35°。 圖4 基于A優化準則的一發四收最優構型示意圖Fig.4 Optimal configuration with one transmitter and four receivers based on A-optimality criterion (31) |θi-θj|=2θ0 (32) 式中:θ0=arccos(1/3)。因此奇數個接收機對應的最優角度為 (33) 圖5 M=3時的變化范圍Fig.5 Variation of when M=3 圖6 基于A優化準則的奇數個接收機最優構型Fig.6 Optimal configuration with odd number of receivers A-optimality criterion (34) A準則下3個接收機最優構型對應的FIM矩陣為 (35) 同理,4個接收機最優構型對應的FIM矩陣為 (36) (37) 通常情況下,采用D優化準則與采用A優化準則得到的最優構型相同,而通過本節分析,在TOA橢圓定位中,基于A優化準則得到的最優構型與D優化準則的最優構型不同,其最優構型與接收機數目的奇偶性有關。兩種優化準則均可以作為優化目標函數作為定位性能好壞的標準。 第2節給出了不考慮接收機平臺約束情況,TOA定位跟蹤最優構型的解析解。但在實際應用中,集群接收平臺受到自身運動約束的影響,無法在短時間內達到對目標定位最優構型的條件[16]。尤其是在沒有目標先驗信息的情況下,目標與航空集群之間的距離可能較遠,受到平臺速度、轉彎角速度等影響,需要經過一定時間才能夠達到最優的定位跟蹤構型,才能夠得到更好的定位效果。因此如何將理論推導的最優構型應用到集群航跡優化中,提升對目標的定位跟蹤效果是本節需要解決的問題。 假定航空集群接收機系統的離散動態模型[17]為 Xk+1=f(Xk,uk) (38) 式中:Xk為k時刻系統的狀態值,Xk=[x1(k),x2(k),…,xi(k),…,xM(k)]T,xi(k)為k時刻接收機i的位置;uk為每個時刻集群接收機平臺飛行方位角的控制量,uk=[u1(k),u2(k),…,ui(k),…,uM(k)],ui(k)為k時刻接收機i的飛行方位角控制量。由此可得離散情況下航空集群的運動方程可以簡化為 (39) 式中:v0為平臺飛行速度;T為接收機采樣時間間隔。如圖7所示,在每一采樣時間內,應用定位算法更新目標位置,計算目標位置更新后接收機相對發射機與目標連線的角度θ=[θ1,θ2,…,θM]T,同時分別以A、D優化準則為優化目標函數,得到下一時刻各個接收機的控制量uk+1,因此目標函數與平臺約束可以表示為[18] 圖7 航空集群尋找最優航跡示意圖Fig.7 Schematic diagram of finding optimal trajectory for aircraft swarm (40) s.t.‖ui(k+1)-ui(k)‖≤umax (41) ‖xi(k+1)-xt(k)‖≤Rh (42) ‖xi(k+1)-xt(k)‖≥Rl (43) ‖xi(k+1)-xj(k+1)‖≤ch (44) ‖xi(k+1)-xj(k+1)‖≥cl (45) 式中:約束條件式(41)表示平臺自身方位角約束,它限制了生成的航向最大偏角umax,該約束取決于集群平臺的機動性能;條件式(42)、式(43)分別表示集群平臺到目標之間的距離約束,距離上限Rh主要由接收機接收信號的信噪比決定,距離下限Rl為集群平臺與目標之間的安全距離;條件式(44)、式(45)分別為平臺之間通信約束以及集群內平臺防相撞約束,ch、cl分別為平臺之間距離的上限和下限。 由上面航跡優化問題可以轉變為帶約束的非線性優化問題,本文直接借鑒自適應懲罰函數的方法[19]進行求解。 綜上可得,基于A、D優化準則(實際應用過程中A、D優化準則選擇其中一個)的航空集群有源定位航跡優化方法的數據處理流程如圖8所示,其步驟如下: 圖8 基于A/D優化準則的航空集群航跡優化處理流程Fig.8 Trajectory optimization process of aircraft swarm based on A/D-optimality criteria 步驟1給定時刻航空集群接收機系統狀態Xk=[x1(k),…,xM(k)]T,發射機發射波束,各接收機接收目標反射波束,得到接收機的TOA量測值,以及約束條件式(41)~式(45)。 步驟2利用3次最小二乘TOA定位算法[20]求解出當前時刻對目標的估計值t(k)。 步驟3以該時刻目標估計值當做該時刻目標真實值,在約束條件式(41)~式(45)情況下,利用智能優化算法產生各個接收機下一時刻可行的控制量,分別計算在不同控制量uk+1下,接收機相對發射機與目標連線的角度θ=[θ1,θ2,…,θM]T,分別計算以A、D優化準則為優化目標函數式(40)。 步驟4利用自適應罰函數法將該非線性約束轉化為極小化輔助函數的無約束問題,先通過尋優找出遺傳算法中具有較好質量的不可行解,然后再引導種群向可行域或者最優解逼近,記錄該最優解對應的接收機控制量。 航空集群中接收機的初始運動狀態為x1(1)=[-9 200 m,-5 000 m]T、x2(1)=[-10 000 m,-5 000 m]T、x3(1)=[-10 000 m,-5 800 m]T、x4(1)=[-9 200 m,-5 800 m]T。初始時刻各個接收機的機頭指向均為π/2(朝向y軸),固定飛行速度為v0=200 m/s采樣時間間隔T=1 s,仿真時間為150 s。集群平臺的航向角約束為umax=15°,最大和最小探測距離分別為Rmax=20 km、Rmin=0.3 km。 圖9給出了基于D優化準則與A優化準則的航跡對比。由圖9(a)與圖9(b)可知:當發射機與目標靜止,3個接收機自動分為兩個子群朝向目標飛行,同時兩個子群與目標之間的夾角不斷擴大并分別位于發射機與目標連線的兩側;大約經過140 s,兩個子群與該連線之間的夾角均為60°,與理論分析相吻合。圖9(c)與圖9(d)給出了基于A優化準則的飛行航跡。與D準則形成的優化航跡的形狀大致相同,不同之處在于,最終與目標形成的最優構型角度不同。 圖9 基于D優化準則與A優化準則的航跡對比Fig.9 Trajectory comparison based on A and D-optimality criteria 圖10給出了基于D優化準則與A優化準則的誤差對比,整體上A準則對應的平均誤差值相對較小,但對應的計算量較大對應的求解需要的時間較長,同時在某些時刻求解CRLB值的過程中有奇異值的出現,導致算法的穩定性弱于D優化準則。因此在實際應用中,可以優先采用D優化準則,能夠在提升精度的同時確保算法的穩定性與實時性。 圖10 基于D優化準則與A優化準則的誤差對比Fig.10 Error comparison based on A and D-optimality criteria 4.1節對TOA橢圓定位的最優構型進行驗證,因此本節主要針對實際運用過程中發射機、目標均運動情況下,進行驗證。 假設集群平臺之間的通信距離約束為ch=15 km,防相撞約束為cl=0.2 km。采用D優化準則得到的優化后定位結果如圖11所示。 圖11 航空集群有源定位優化Fig.11 Active localization optimization of aircraft swarm 由圖11(a)可得,3個接收機依然按照圖10類似的航跡飛行,同時由于發射機、目標的位置處于動態變化中,接收機每個時刻均按照新的位置進行構型優化,最終得到優化后飛行航跡。 在實時性方面,基于A/D優化準則的航空集群航跡優化方法中最大的計算量來源于優化算法對各個接收機最優控制量的計算。為了保證優化算法能夠高動態的航跡規劃任務。實際仿真中,一是充分考慮集群平臺的航向角約束umax=15°,從而將每個步長中的尋優范圍約束到[-15°,15°]之間,大大縮小了尋優空間;二是采用了自適應罰函數與遺傳算法相結合,充分利用罰函數法的優點,進一步減小了算法計算量,保證了實時性。 為了對構型優化有效性進行驗證,將經過構型優化后的定位結果與接收機隨機產生航跡點的定位結果進行對比,結果如圖11(b)所示。通過圖11(b)對比可得,未經過構型優化的定位結果誤差較大且具有較大的不穩定性,主要因為在某些時刻集群接收機平臺與目標的相對構型非常不利于對目標的定位。采用D優化準則的優化航跡能夠在盡可能短的時間內降低定位誤差,且具備持續優化能力。 本文針對航空集群一發多收有源協同定位運用問題,研究了一發多收有源協同定位最優構型與航跡優化方法。得出以下主要結論: 1) 基于A優化準則與D優化準則推導了不同接收機數目對目標進行定位的最優幾何構型,分析最優構型的解析解,進一步提升有源協同定位效果,為航空集群有源定位構型優化提供了理論支撐。 2) 將得到的最優構型運用到航空集群航跡優化中,提出基于A/D優化準則的航空集群有源定位航跡優化方法,并通過仿真驗證了其有效性。





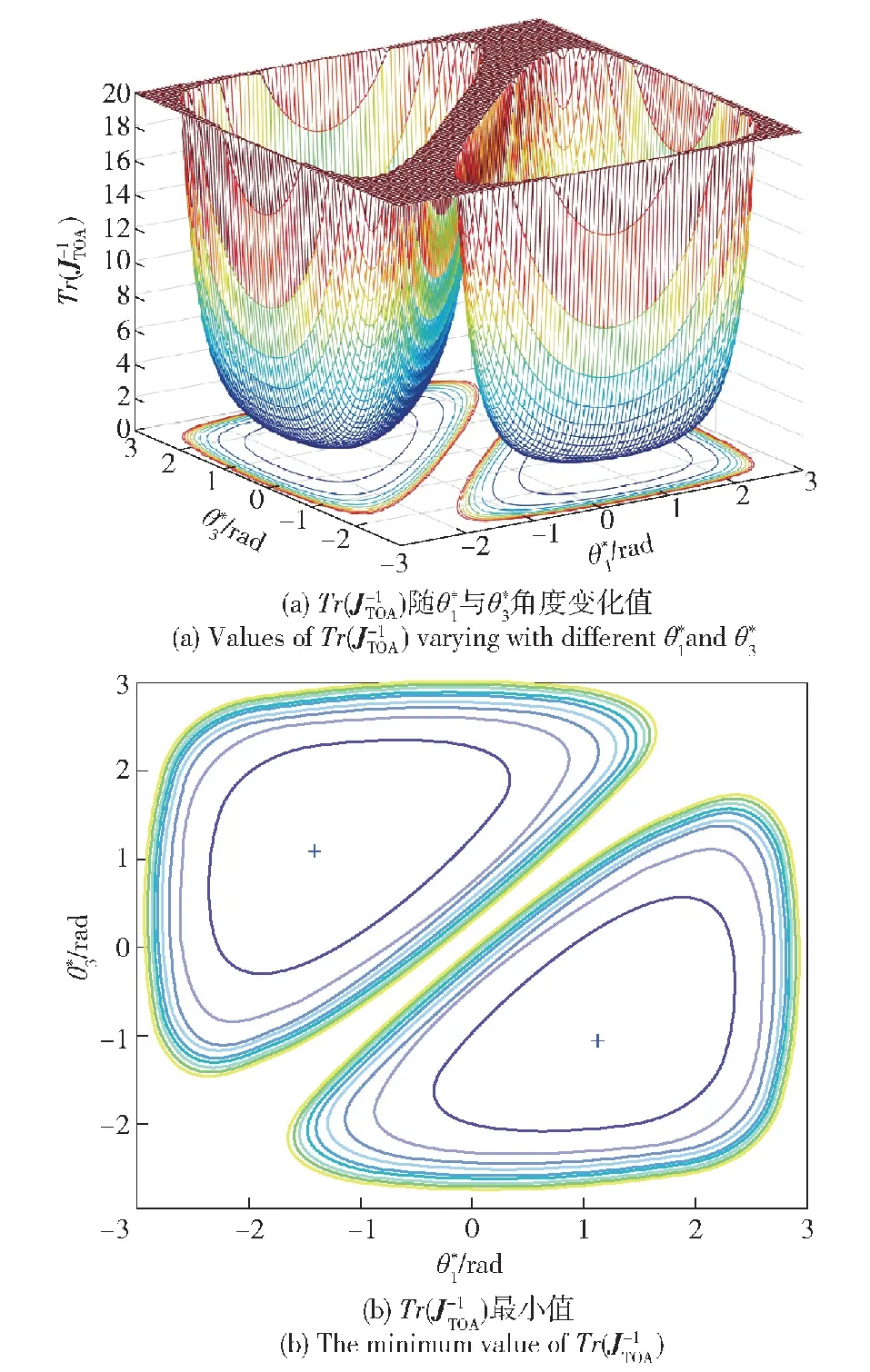
2.2 基于A優化準則的一發多收最優構型分析






3 航空集群有源協同定位航跡優化



4 仿真驗證
4.1 TOA橢圓定位最優構型驗證



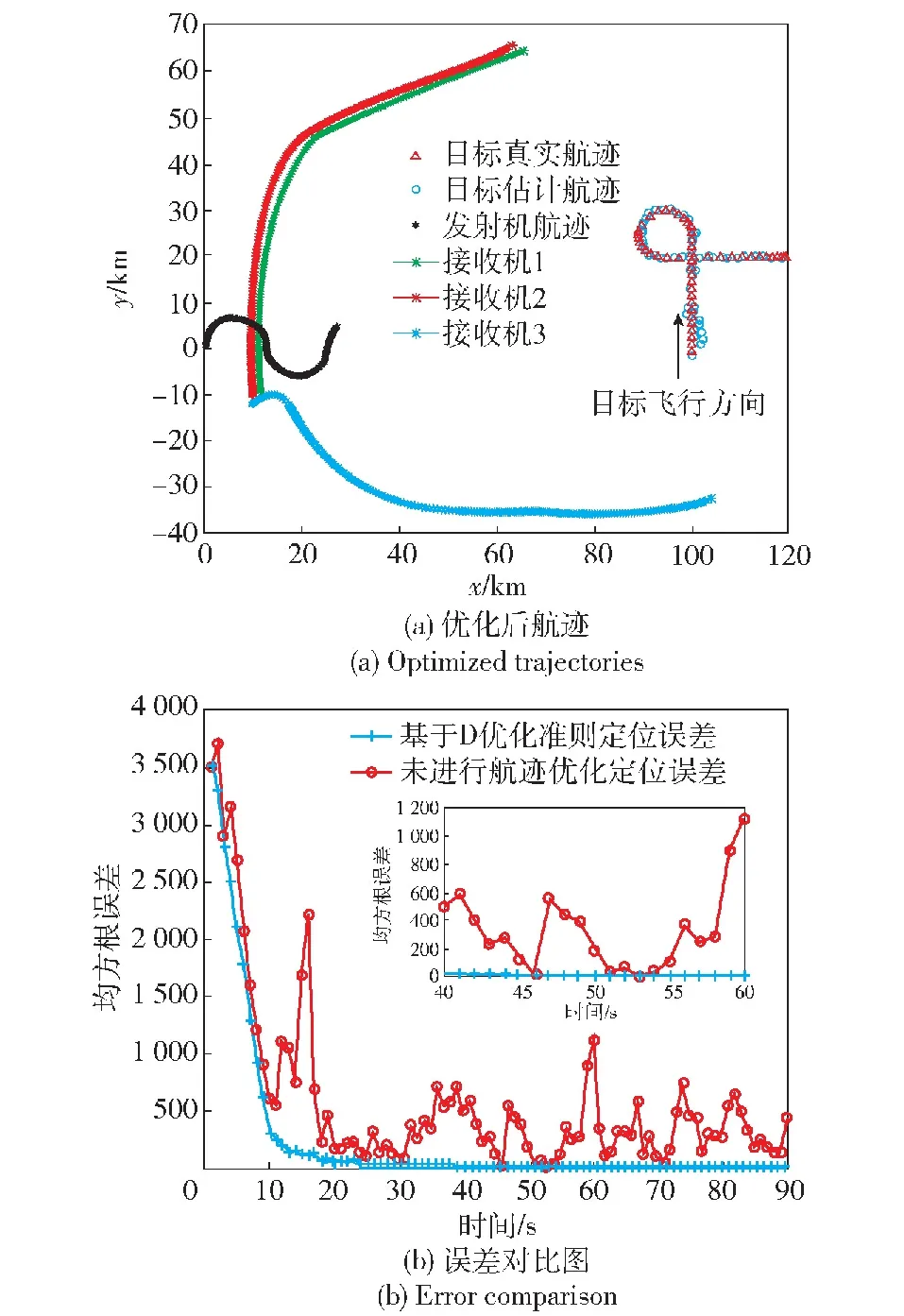
4.2 航跡優化
5 結論

