考慮鏟鉆刀具倒棱刃口幾何參數的鉆削力理論模型

王貴林,于愛兵,鄒翩,李毅,李克凡,吳森凱

(寧波大學 機械工程與力學學院,浙江 寧波 315211)

0 引言

鏟鉆是一種結構簡單、易于制造的孔加工刀具,具有麻花鉆的剛性和槍鉆的韌性,采用內冷系統,有利于切屑排出,可針對被加工材料選擇刀片[1]。當刀片磨損后只需更換刀片,刀片還可重磨,提高了加工效率,節約成本。鏟鉆對機床的剛度要求不高,可用于數控車床、加工中心等大多數設備,廣泛用于鉆削速度高、進給量大和鉆削精度要求高的深孔加工,如飛機起落架的筒形件、船用柴油發動機的缸頭主軸螺栓孔和主油道等均采用鏟鉆一次加工完成。鏟鉆刃磨過程中刃口會出現裂紋、缺口等微觀缺陷,降低鏟鉆刀片的使用壽命,在刀具制造過程中需要將鏟鉆刃口加工成倒棱形狀,以有效減少刃口微觀缺口,延長刀具壽命[2-3]。但是,倒棱刃口的存在會影響鉆削力,而鉆削力對工件表面形貌、尺寸精度和刀具磨損具有顯著影響[4],鉆削力同時也是鏟鉆刀具設計、開發和應用中的重要參考依據之一。因此,有必要研究考慮倒棱刃口幾何參數的鏟鉆鉆削力。

目前,鏟鉆鉆削力模型都是基于鋒利刃口建立的,并沒有考慮倒棱刃口的幾何參數,限制了高性能鏟鉆的工程設計和應用。一些研究人員針對銑刀、車刀和聚晶金剛石(Polycrystalline diamond,PCD)復合片鉆頭等刀具建立了考慮倒棱刃口的切削力模型。W?ste等[5]考慮倒棱銑刀加工引起的過程阻尼效應和倒棱刃振動速度,基于幾何物理建立了銑削力模型。Weng等[6]考慮倒棱寬度對切削力的影響,引入改進因子修正鋒利刃口車刀的切削力模型。Zhuang等[7]在車刀刃口力系數引入倒棱寬度和角度,并基于斜切削理論建立了切削力預測模型。Hotz等[8]通過切削力與車刀倒棱角度之間的線性擬合,建立了車刀倒棱角度與切削力的函數關系。莊可佳等[9]在滑移線場理論的基礎上引入了負前角車刀倒棱角度和寬度,得到了負前角倒棱車刀的正交切削力理論公式。Shao等[10]在銳邊PCD復合鉆頭與巖石相互作用模型的基礎上引入了PCD復合片鉆頭的倒棱寬度,建立了關于PCD鉆頭倒棱寬度的鉆削力模型。但是,由于鏟鉆刀具結構不同于銑刀、車刀、PCD復合片鉆頭,上述倒棱刀具的切削力理論公式不能直接用于鏟鉆。所以,有必要探索和研究考慮倒棱刃口幾何參數的鏟鉆鉆削力理論模型。

本文基于鏟鉆倒棱刃口的幾何關系,提出一種考慮鏟鉆倒棱角度和寬度的鉆削力理論模型,并引入變形系數替代剪切角和摩擦系數以便于鉆削力的工程計算,提高鉆削力模型在工程中的實用性,通過鉆削力實驗和有限元仿真驗證本文建立的鉆削力模型,為倒棱刃口鏟鉆的設計和開發提供參考。

1 鉆削實驗及仿真

1.1 鉆削實驗

實驗選用榮科數控刀具有限公司產14.00G2SA型硬質合金鏟鉆刀片,直徑為φ14 mm,刀片前角γo=15°、后角αo=8°和頂角2φ=132°,鏟鉆分屑槽數量λ=2,分屑槽寬度a=0.8 mm。如圖1所示,鏟鉆刀片倒棱刃口的幾何參數包含倒棱寬度b、刃口角度γ,這兩個參數的定義分別為：倒棱刃口在基面上投影的長度為倒棱刃口寬度b,刀具基面與倒棱面的夾角(銳角)為倒棱角度γ。鉆削實驗選取倒棱刃口的幾何參數,如表1所示。

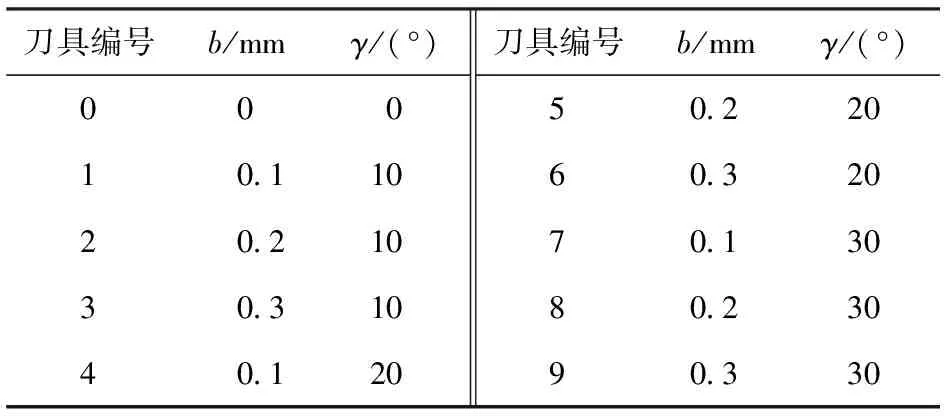
表1 鉆削實驗的鏟鉆刀片倒棱刃口參數Table 1 Chamfered edge parameters of spade drill inserts in drilling experiments

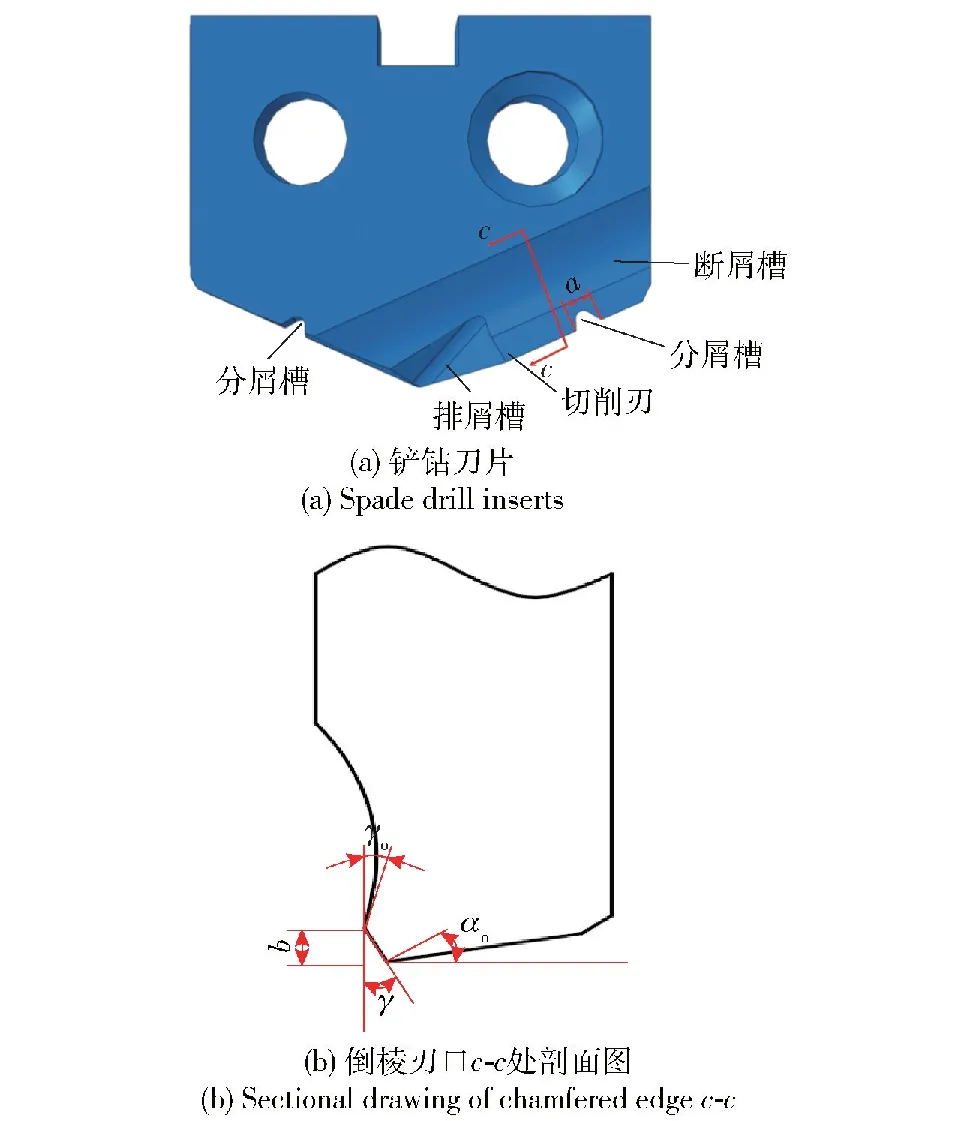
圖1 鏟鉆刀片及倒棱刃口剖面圖Fig.1 Sectional drawing of spade drill insert and chamfered edge

選用牌號為7075-T651鋁合金為工件材料,尺寸為150 mm×100 mm×5 mm,在工件上加工出直徑為φ6 mm的預制孔。實驗裝置如圖2所示,在VF-2立式數控加工中心(哈斯自動數控機械(上海)有限公司生產)進行鉆削實驗,選擇進給速度f=0.2 mm/r,鉆削速度vc=70 m/min;用側固式刀柄BT40-SLN20裝夾直徑為φ20 mm的SD00H-64-XP20型鏟鉆刀桿,通過夾具工件固定到瑞士Kistler公司產9257B三向測力儀;測力儀將收集的信號傳送到信號分析儀對信號進行處理后,再通過Dynoware軟件輸出鉆削力曲線;鉆孔后采集切屑,測量切屑厚度,在切屑不同位置多次測量切屑厚度的平均值,以減小測量的誤差。

圖2 鉆削力測試實驗裝置Fig.2 Drilling force test experimental devices

1.2 鉆削仿真

按照表1中的倒棱刃口幾何參數建立鏟鉆刀片的三維模型,為減少計算時間,把鏟鉆刀片定義為剛體,通過有限元模擬鏟鉆鉆削過程,分析鉆削力和扭矩的變化規律。在實際鉆削過程中,鋁合金會發生高變形率和高溫,為此本文選用溫度-位移耦合算法。鉆削模型的邊界條件和網格如圖3所示,將工件外圈固定,限制工件的6個自由度,根據實驗條件在工件模型上設置直徑為6 mm的預制孔。三維仿真計算中,工件應盡量采用結構化網格得到六面體網格,以較小的計算量、較短的計算時間獲得較高精度計算結果[11]。因此工件單元類型采用六面體,采用結構化網格;刀具單元類型采用四面體,網格劃分技術采用自由網格劃分;工件網格單元數量為 254 016,刀具網格數量為31 667。鉆削速度vc=70 m/min,進給速度f=0.2 mm/r。Johnson-Cook本構模型可以描述材料在高溫、高應變和高應變下的塑性行為[12],因此結合鉆削的實際情況,本文選用Johnson-Cook模型作為鋁合金7075-T651的材料本構模型[13],其表達式為

圖3 鉆削模型的邊界條件和網格Fig.3 Boundary conditions and meshes of the drilling model

(1)

選擇Johnson-Cook斷裂失效標準作為切屑的分離標準,該失效標準考慮到了材料的應變、應變率、溫度和壓力[14],可以有效反映鉆削過程中的切屑分離[15],其表達式為

(2)

式中：εf為材料失效應變;d1～d5為失效參數。

鋁合金7075-T651的Johnson-Cook本構方程和失效模型的參數如表2[16]所示,鋁合金7075-T651的材料性能如表3[17]所示,硬質合金刀具的性能參數如表4[18]所示。

表2 7075-T651鋁合金的Johnson-Cook材料參數[16]Table 2 Johnson-Cook material parameters of 7075-T651alloy[16]

表3 7075-T651鋁合金的熱性能和力學性能[17]Table 3 Thermal and mechanical properties of 7075-T651 alloy[17]

2 鉆削力理論模型

首先,在正交切削的基礎上[19],計算出鏟鉆單個切削刃在相對于主切削刃方向的切向力和法向力。然后,根據鏟鉆切削刃的傾斜角度,確定出鏟鉆單個切削刃上微分單元的軸向力和扭矩,并對微分單元的力進行積分,得到倒棱刃口鏟鉆的軸向力和扭矩。最后,考慮鏟鉆分屑槽對切屑截面面積和切削刃寬度的影響,并引入變形系數對公式進行簡化。

2.1 鏟鉆單個切削刃的受力分析

圖4 第1變形區下邊界理想輪廓的受力分析Fig.4 Force analysis of the ideal contour of the lower boundary of the primary deformation zone

在正交切削中第1變形區的下邊界由面OA′和面A′B′組成,且平面A′B′以θ=45°傾斜于平面OA′[20](見圖4)。設鏟鉆切削寬度為W,在第1變形區的下界邊平面A′B′、OA′上的分力為

OA′所在的平面的剪切力：

FS1=τs1WL

(3)

OA′所在的平面的法向力：

Fp1=σp1WL

(4)

A′B′所在平面的剪切力：

FS=τsWL0

(5)

A′B′所在平面的法向力：

Fp=σpWL0

(6)

式中：τs1為作用于面OA′上均勻分布的剪應力;σp1為倒棱刃口前方的工件材料中存在的拉伸應力,方向垂直于OA′;τs、σp分別為作用在A′B′面上均勻分布的剪應力和正應力,且在下邊界OA′B′上滿足τs=σp=τs1,τs在數值上等于工件材料的屈服剪應力。

鏟鉆受到的力與作用在第1變形區下邊界的力保持平衡,因此作用在鏟鉆上的分力為

F′h=Fscosθ+Fpsinθ+Fs1=τsWt1(cotφo+1)

(7)

F′v=Fssinθ-Fpcosθ+Fp1=σp1Wt1(cotφo-1)

(8)

為計算鏟鉆倒棱在鉆削過程中受到的力,將圖4中的倒棱刃口處局部放大,分析倒棱刃口處工件材料流動模式如圖5所示,刃口D處下方的材料必須穿過鏟鉆刃口下方并受到壓縮產生變形。假設D下方的材料受壓縮產生的變形為彈性變形,則材料穿過DE區域后,將彈性恢復并與后刀面EF接觸。D上方的工件材料向上移動,而D下方的工件材料向下移動,因此,D之前的工件材料必須承受拉伸應力,即垂直作用于下邊界OA的應力σp1,已經計算在第1變形區的下邊界中,因此下面只需計算出工件材料受刃口DE壓縮而變形所產生的力,便可以計算出鏟鉆受到的力。圖5中,h為變形的深度,b為倒棱寬度,l1為與刃口接觸長度在DF上的投影,l2為材料恢復變形時與后刀面EF的接觸后在DF上的投影,α0為后角。

圖5 工件材料在鏟鉆倒棱刃口的流動模式Fig.5 Flow pattern of workpiece material on the chamfered edge of the spade drill

當αo已知時,l1和l2可表示為

(9)

為了反映工件材料產生變形的深度h與倒棱刃口寬度b的關系,引入幾何系數c,建立關系式如下：

h=cb

(10)

將式(10)代入式(9),可得

(11)

(12)

(13)

將式(11)代入式(12)、式(12)代入式(13),可得鏟鉆倒棱刃口產生的相對于鏟鉆主切削刃方向的法向分力和切向分力為

(14)

因此,鏟鉆在相對于主切削方向的切向合力Fh、法向合力Fv可以分別表達為

(15)

(16)

將式(14)、式(7)、式(8)代入式(15)、式(16),可得到倒棱刃口鏟鉆相對于主切削刃方向的切向力和法向力公式：

Fh=τsWt1(cotφo+1)+μpmWcb(tanγ+cotαo)

(17)

Fv=σp1Wt1(cotφo-1)+pmWcb(tanγ+cotαo)

(18)

2.2 鏟鉆的軸向力和扭矩模型

在2.1節中基于正交切削理論計算出鏟鉆在相對于主切削刃方向的切向和法向力,但是在實際加工過程中鏟鉆的切削刃是傾斜一定角度,如圖6所示。圖6中,鏟鉆半徑為R2,工件材料預加工孔半徑為R1。為計算出鏟鉆的軸向力和扭矩將切削刃進行微分成小單元,選取任意單元進行分析,計算出單元鉆削力,在進行積分后計算出鏟鉆的軸向力和扭矩。

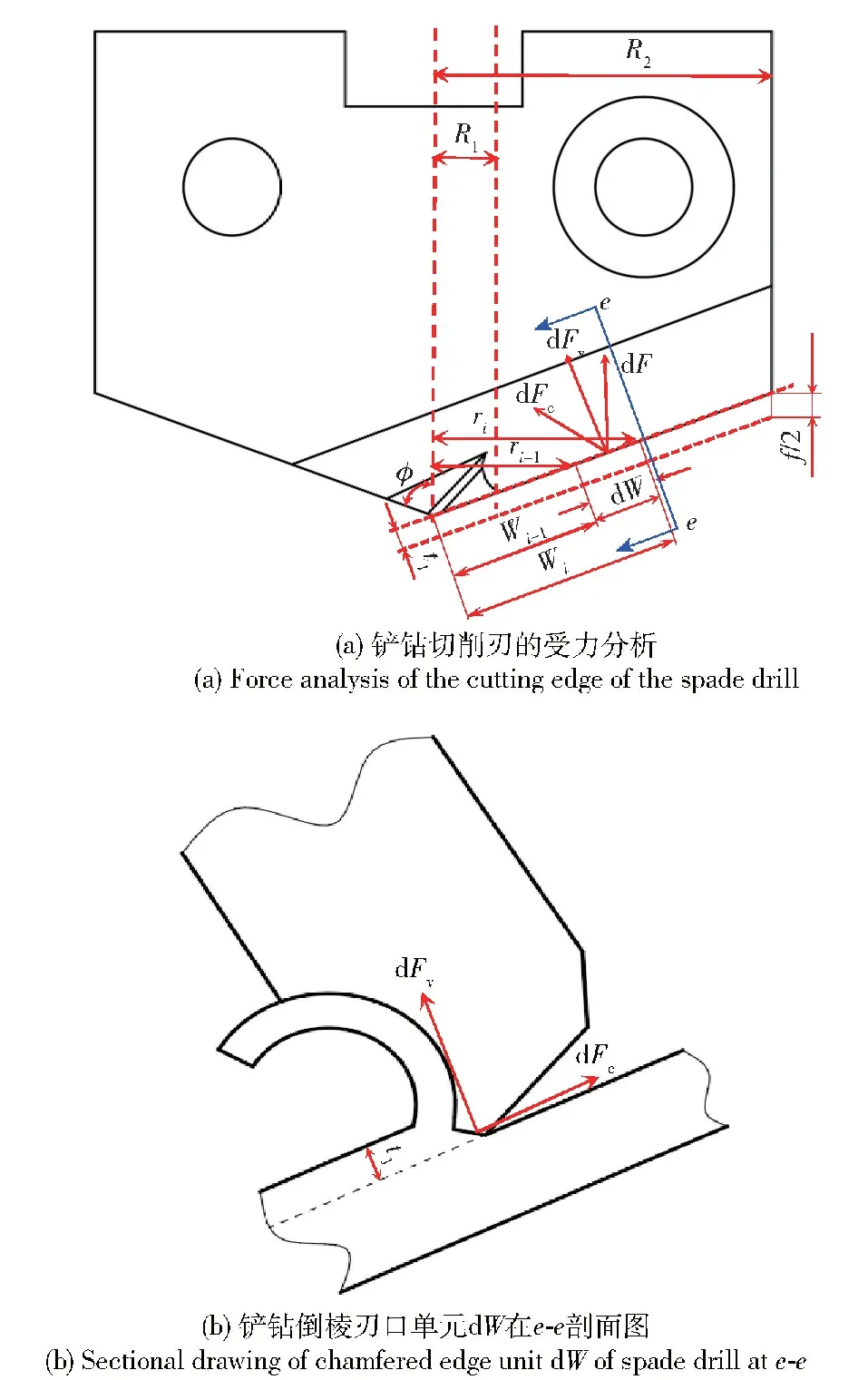
圖6 鏟鉆切削刃單元dW的鉆削力分量Fig.6 Drilling force component of the cutting edge unit dW of the spade drill

將鏟鉆切削刃分為W0,…,Wi-1,Wi,…,Wk共k+1個點,則切削刃有k個小單元ΔW,ΔW=Wi-Wi-1,i=0,1,…,k。設鏟鉆切削刃上的點到鉆削中心軸的徑向距離為ri,考慮一個位于鏟鉆刃口的單元受力,如圖6(b)所示,建立鉆削半徑r、切削寬度W二者的微分關系式。

取切削刃上任意一單元ΔW,根據圖6(a)的幾何關系,可得

(19)

令Δr=ri-ri-1,當Δr無限趨近于0 mm時,可得

(20)

鏟鉆鉆削時未變形切屑厚度t1為

(21)

對式(17)、式(18)進行微分并將式(20)、式(21)代入后,可得到鏟鉆切削刃單元dW的鉆削力,如圖6(b)所示,單元鉆削力可表達為

(22)

(23)

根據圖6(a)的幾何關系可知,單刃鏟鉆切削刃單元dW的扭矩dM和軸向力dF為

(24)

(25)

如圖6(a)所示,ri∈[R2,R1],在r的極限值間進行積分,由于鏟鉆有兩條主切削刃,鏟鉆鉆削力是單刃的2倍,可以得到鏟鉆的扭矩公式為

(26)

同理,可得鏟鉆的軸向力公式為

(27)

2.3 考慮鏟鉆分屑槽的鉆削力模型

鏟鉆分屑槽能夠減少切削寬度,提高斷屑效果。以2.2節中無分屑槽鏟鉆鉆削力為基礎,進一步考慮分屑槽對鉆削力的影響,對鏟鉆鉆削力的模型進行修正,更符合刀具實際結構,同時引入變形系數替代摩擦系數和剪切角便于工程計算和應用。

分屑槽工作原理示意圖,如圖7所示,當切削刃G′G切除工件表面材料時,由于分屑槽的作用,在切除工件表面材料后留下凸形表面輪廓如圖7(c)所示;切削刃H′H切除圖7(c)中所示的表面輪廓,其切除的部分切屑如圖7(e)所示,分屑槽的引入減少了被切除材料的寬度,但是切屑高度增加,因為分屑槽錯開分布,所以鏟鉆的切削刃一次切削切除切屑的橫截面積不變,即Ac=L1t1=[f(R2-R1)]/2(L1為無分屑槽鏟鉆的切削刃寬度,根據圖6(a)可知,L1=(R2-R1)cscφ),但是分屑槽的引入改變了鏟鉆主切削刃的長度,下文中分析切削刃長度對鉆削力的影響。圖7中,λ為鏟鉆的分屑槽數量,h0為分屑槽工作高度。

圖7 鏟鉆分屑槽工作原理示意圖Fig.7 Schematic diagram of the working principle of the chip-split grooves of the spade drill

以圖7(a)中切削刃G′G為例分析切削刃寬度的變化。當鏟鉆存在分屑槽時,切削刃減少的寬度為λa/2;鏟鉆在鉆削加工中每齒進給量較小,因此,分屑槽槽型對h0的影響不大,可將h0表示為h0≈t1=(fsinφ)/2,切削刃寬度增加了λh0,則引入分屑槽后鏟鉆一條切削刃的寬度L′為

L′=L1-λa/2+(nfsinφ)/2

(28)

為得到關于切削刃寬度L1和鏟鉆切削刃一次移除切屑橫截面積Ac的鏟鉆鉆削力公式,令Ac=L1t1=[f(R2-R1)]/2,L1=(R2-R1)cscφ,則式(26)、式(27)變換為

M=(R2+R1)[τsAc(cotφo+1)+
μpmcb(tanγ+cotαo)L1]

(29)

F=2σp1Ac(cotφo-1)sinφ+
2pmL1cb(tanγ+cotαo)sinφ

(30)

式(29)、式(30)表明,如果倒棱幾何參數已知時,則扭矩和軸向力取決于兩個量,一個是切削刃寬度L1,另一個是鉆削一次移除切屑的橫截面積Ac。根據分屑槽的工作原理分析可知,分屑槽的引入會改變切削刃寬度,但是不會影響切屑橫截面積,因此用L′替代式(29)、式(30)中的L1,可得到存在分屑槽的扭矩M和軸向力F的公式為

M=(R2+R1)[τsAc(cotφo+1)+
μpmcb(tanγ+cotαo)L′]

(31)

F=2σp1Ac(cotφo-1)sinφ+
2pmL′cb(tanγ+cotαo)sinφ

(32)

通過式(31)、式(32)可知,要計算出倒棱刃口鏟鉆的軸向力F和扭矩M的數值,就必須知道公式中剪切角φo和摩擦系數μ,但是在實際加工過程中很難直接獲得剪切角φo和摩擦系數μ,導致計算公式的實用性差,因此引入變形系數來代替剪切角φo和摩擦系數μ;同時,通過變形系數反映切削參數的變化對鉆削力的影響,變形系數ξ[21]可表示為

(33)

式中：t2為鉆削后切屑厚度。

切削機理的研究表明,剪切角φo、摩擦角βo和變形系數ξ[22]應滿足以下關系：

(34)

(35)

式中：γo為刀具前角。摩擦系數可表示為

μ=tanβo

(36)

根據式(34)、式(35)、式(36),可以將摩擦系數μ表示為

(37)

式(34)、式(35)、式(37)代入式(31)、式(32),可得引入變形系數簡化后的鏟鉆軸向力和扭矩分別為

(38)

(39)

鏟鉆扭矩和軸向力表達式(38)、式(39)中的邊界應力τs、流體靜壓力pm、拉伸應力σp1是與工件材料相關的常數,切削刃寬度L′和橫截面積Ac為刀具結構相關的常數。幾何系數c、變形系數ξ、倒棱刃口的幾何參數b和γ為變量,其中幾何系數c、變形系數ξ、倒棱刃口寬度b與鏟鉆的鉆削力F呈正比關系;本文選用的后角αo=8°,則倒棱角度γ與鏟鉆的鉆削力呈反比關系。

3 結果與討論

3.1 鉆削力模型驗證

針對本文鉆削實驗的條件,計算出式(38)、式(39)中工件材料常數和刀具結構常數,通過文獻[20]、文獻[23-24]建立的公式分別計算出法向拉伸應力σp1=425.62 MPa、流體靜壓力pm=1 560 MPa和圖4中邊界AB上的剪應力τs=300.2 MPa;鏟鉆切削刃長度L′=3.76 mm;鏟鉆切削刃一次移除切屑橫截面積Ac=0.4 mm;將上述的常數代入式(38)、式(39),可得軸向力和扭矩計算公式分別為

(40)

F=322.14(ξ-1.2)+10 716.98cb(tanγ+7.12)

(41)

根據式(33)計算出倒棱鏟鉆切屑的變形系數ξ,如表5所示。取穩定鉆削階段的扭矩曲線均值為扭矩[25],并通過預實驗算出扭矩的平均值,再根據式(40)確定出幾何參數c的參考值如表5所示。將表5中變形系數和幾何系數的結果代入軸向力的計算式(40)、式(41)中,便可以計算出倒棱鏟鉆軸向力和扭矩。

表5 理論模型參數Table 5 Values of theoretical model parameters

鉆削力公式計算結果、鉆削力試驗測試結果以及軸向力和扭矩有限元模擬結果如圖8所示。軸向力而言,計算結果與鉆削實驗結果的平均誤差3.00%,計算結果與模擬結果的平均誤差為4.31%;就扭矩而言,計算與實驗的平均誤差5.52%,計算與模擬的平均誤差6.73%。如果鉆削力公式計算值與實驗值之間的平均誤差在10%以內,則說明鉆削力公式是可靠的[26]。上述4項平均誤差均小于10%,表明本文建立的鉆削力公式是可靠的。將圖8分為Ⅰ、Ⅱ、Ⅲ 3個區域,分別對應鏟鉆倒棱角度的10°、20°、30°,在每一區域中有3把刀具,倒棱寬度b依次為0.1 mm、0.2 mm和0.3 mm,在3個區域中,均呈現出鉆削力隨倒棱寬度b增大而增大的趨勢,如在區域Ⅲ中,F9>F8>F7,M9>M8>M7,其中字母下標為刀具序號。同樣,在區域Ⅰ和Ⅱ中也可以觀察到相同的鉆削力變化趨勢。通過式(40)、式(41)可知,當倒棱角度γ不變時,軸向力和扭矩與倒棱寬度b呈線性關系,因此,在3個區域內,可以分別觀察到鉆削力隨著倒棱寬度增大而逐漸增加的趨勢。

圖8 模擬、計算和鉆削實驗的軸向力和扭矩Fig.8 Axial forces and torques from simulation, theory and drilling experiment

3.2 鉆削力對比

倒棱刃口和鋒利刃口鏟鉆鉆削實驗測試的軸向力、扭矩進行對比如圖9所示,圖9中0號刀具為鋒利刃口鏟鉆,1～9號刀具為倒棱刃口鏟鉆。軸向力和扭矩隨著倒棱寬度b的增大而增大,當倒棱寬度b較小時,軸向力和扭矩隨著倒棱角度γ的增大呈現先增大、后減小的趨勢。根據圖9計算出倒棱刃口相對于鋒利刃口的軸向力和扭矩增長率如圖10所示,倒棱刃口鏟鉆相對于鋒利刃口鏟鉆的軸向力增加了34.47%～259.22%,扭矩的增加了8.52%～82.01%。隨著倒棱刃口幾何參數的變化,倒棱刃口鏟鉆相對于鋒利刃口鏟鉆的軸向力和扭矩均存在顯著的變化,因此,建立倒棱刃口鏟鉆的鉆削力公式是有必要的。將圖10分為Ⅰ、Ⅱ、Ⅲ 3個區域,分別應對倒棱角度為10°、20°、30°的鏟鉆刀具,在Ⅰ、Ⅱ、Ⅲ區域內,倒棱寬度b為0.1 mm時,鏟鉆扭矩和軸向力的增長率最小,b為0.3 mm時,倒棱鏟鉆鉆削力的增長率最大;倒棱角度γ=20°時,鏟鉆的軸向力和扭矩增長率最為顯著,在倒棱角度γ=10°或γ=30°、倒棱寬度b=0.1 mm時,軸向力和扭矩增長率最小。因此,在設計鏟鉆倒棱時,應避免選擇鏟鉆倒棱寬度b=0.3 mm,倒棱角度γ=20°,即避免鏟鉆的軸向力和扭矩過大。所以,結合軸向力和扭矩的對比結果,在設計鏟鉆刀具時,可以得到倒棱刃口幾何參數的合理取值范圍。例如,根據圖10的對比結果,如果設計倒棱刃口鏟鉆刀具時,則應該優先選擇倒棱寬度0.1 mm,然后選擇倒棱角度為10°或30°,這樣可以獲得較小的軸向力和扭矩的增長率,避免產生較大的鉆削力。

圖9 鋒利刃口和倒棱刃口鏟鉆軸向力和扭矩的對比Fig.9 Comparison of axial force and torque between spade drills with sharp cutting-edge and chamfered edge

圖10 倒棱刃口相對于鋒利刃口鏟鉆軸向力和扭矩增長率Fig.10 Growth rates of axial force and torque of spadedrill with chamfered edge relative to that with sharp cutting-edge

4 結論

本文提出一種考慮鏟鉆倒棱角度和寬度的鉆削力理論模型,并引入變形系數替代剪切角和摩擦系數。同時,通過鉆削力實驗和有限元驗證鉆削力模型,并將倒棱刃口鏟鉆鉆削力與鋒利刃口鉆削力進行對比。得出以下主要結論：

1)本文建立了倒棱刃口幾何參數的鉆削力模型,并通過有限元和鉆削實驗驗證了鉆削力模型,結果表明鉆削力模型可用于含有倒棱刃口的鏟鉆刀具軸向力和扭矩的計算。

2) 通過倒棱刃口鏟鉆和鋒利刃口鏟鉆軸向力和扭矩的對比,可以得到倒棱寬度b和角度γ對鏟鉆鉆削力的影響規律,并在設計鏟鉆刀具時,鏟鉆刃口的倒棱寬度選擇0.1 mm,倒棱角度選擇10°或30°可以獲得較低的鉆削力。