面向數學核心素養的初中數學微專題設計研究與實踐

張永念

摘 要：學生的綜合素質培養是初中階段教學的重要目標，而其中核心素養的培養則是重中之重.通過數學核心素養來對數學試題進行研究能夠有效促進教師在教學的過程中對數學核心素養的理解，從而能夠更好地來實現對初中生進行數學核心素養的培養.本文將結合數學試題來對數學核心素養的培養進行探討.

關鍵詞：初中數學；數學核心素養；實踐

隨著我國素質教育以及新課改的全面推行，數學核心素養的培養成了數學教學過程中的重點問題.初中是學生進行數學學習的重要時期，也是進行數學核心素養培養的重要時期，所以采用正確的方式來進行數學核心素養的培養對于初中數學的教學有著非常重要的意義.在培養數學核心素養的過程中，通過數學試題可以加強教師對數學核心素養的理解，從而更好地實現對初中學生進行數學核心素養的培養.而數學的核心素養主要包括數學抽象、邏輯推理、數學建模、直觀想象、數學運算以及數據分析這些內容，本文結合這方面的例題來對數學核心素養的培養進行探討.

1 數學抽象

例1 甲乙兩人分別從直線距離100km的A、B兩地同時出發相向而行，已知甲的速度為6km/h，乙的速度為4km/h，甲出發時帶著一條小狗同時出發，小狗的速度為12km/h，當小狗遇到乙后掉頭朝甲走，小狗遇到甲后朝乙走，直到甲乙兩人相遇，小狗在兩人相遇的過程中一共走了多少米？

分析：這個問題如果從小狗的角度出發來進行計算的話，需要對小狗的運動過程進行動態的分析，小狗的運動過程就太過復雜，同時進行解答也需要花費大量的時間.但是如果在解題的過程中從數學抽象的角度出發，就可以知道當兩人相遇時小狗也會停止移動.這樣小狗的移動時間是和兩人的移動時間是相同的，所以只需要來計算兩人相遇所需要的時間100÷（6+4）=10小時.這樣就能夠計算出小狗所運動的距離了.

解：甲乙兩人相遇的時間為：

100÷（6+4）=10（h），

所以小狗行走的時間也是10（h），

所以小狗移動走了10×12=120（km）.

回顧：本題主要就是對數學抽象這一數學核心素質的考察，從小狗的角度分析問題需要進行大量的計算，而通過數學抽象將問題進行轉化就能夠快速的解決.所以在對學生進行數學抽象性的培養過程中需要保留數學中所包含的“物理屬性”以及“具體屬性”來幫助學生認識到數學的本質，從而能夠輕松解決問題.

2 邏輯推理

回顧：數學建模的方式是將抽象的問題進行直觀的展示，通過數學語言的方式表示問題的本質，然后通過數學的相關知識和方法來構建數學模型從而實現對問題的解決.本題主要采用的建模方式就是利用勾股定理的方式來構造直角三角形，將函數的每一項看成是直角三角形的兩個直角邊求斜邊的過程.從而進一步的建立矩形來將球函數的最小值轉化成求矩形對角之間的最短距離的問題.通過數學建模的方式能夠將數學問題進行巧妙的轉化，從而實現對問題進行更好的解答.

4 直觀想象

例4 已知x滿足（x-2016）²+（2017-x）²=1，那么（2017-x）（x-2016）=________.

分析：本題是一道填空題，那么在對這道題的求解過程中就不一定需要對這個題進行相關的數學運算.通過對題目中的（x-2016）²+（2017-x）²=1情況進行觀察可以發現，要讓這個式子成立則x-2016，2017-x這兩個中必然會出現一個的值為0，一個的值為1的情況，那么將這個情況帶入到（2017-x）（x-2016）中就可以得到這個題的答案為0.

回顧：在這個例題的解題過程中采用了直觀想象的方式.但是直觀想象是一種數學直覺而不是瞎猜，它是建立在對數學基礎知識以及解題經驗的積累上的，通過對解題經驗和基礎知識的逐漸積累來形成一種數學直覺，從而能夠對數學問題進行快速的判斷.通過數學的直觀想象能解題過程中對數學問題進行判斷，從而提升解題的效率，需要初中學生有扎實的數學基礎知識和豐富的解題經驗.

5 數學運算

例5 根據國家統計局數據，2021年全年國內生產總值為1143670億元，比2020年增長了8.1%.假設國內生產總值的增長率不變，則國內生產總值突破130萬億的年份是（）.

A. 2022年

B. 2023年

C. 2024年

D. 2025年

解析：本題主要是需要對具體的數字進行計算，那就需要按照題目給出的條件來計算出后續幾年的國內生產總值的數據.首先是A選項2022年的國內生產總值的數據的計算方式為1143670×（1+8.1%）=1236307.27＜1300000，答案A是錯誤的.2023年的國內生產總值的數據的計算方式為1143670×（1+8.1%）²，可以在將計算方式變為在2022年的基礎上增長8.1%的情況，即1236307.27×（1+8.1%）≈1336448.16＞1300000.所以正確答案是選B，后續的C、D兩個選項也可以根據相關的計算方式來對生產總值進行計算.

回顧：數學運算是學習數學知識過程中必須要掌握的一項數學核心能力.本題主要考察的就是學生數學的運算能力.在解題的過程中對于B、C兩個答案的計算可以通過完全平方公式和完全立方公式來進行估算結果.在計算的過程中需要保證計算的準確性.

6 數據分析

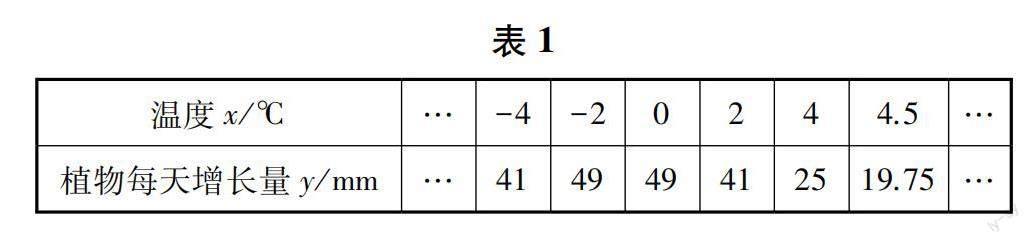
例6 科學家將一種植物分別放入不同的溫度環境下來對植物每天的高度增長情況進行觀察，如表1所示.通過這些數據，科學家對植物每天生長的高度y與溫度x的函數關系進行了推測.（1） 請問函數的關系是什么函數，并求出函數關系式.（2） 當溫度為多少時植物每天的生長高度最大？（3） 如果保持溫度不變，要讓植物10天生長的高度總和大于250mm，那么溫度選擇的范圍是？

分析：通過對本題的分析首先需要確定植物生長高度y與溫度x的函數關系.通過對數據情況的觀察和分析，因為表中出現了（0，49）這組數據，則函數就不可能是反比例函數，同時點（-2，49），（0，49），（2，41）這三個點不在同一條直線上，所以函數關系也不可能是一次函數，所以通過分析，該函數關系應該是二次函數.通過函數過點（-2，49），（0，49）可以知道函數的對稱軸為x=-1，則假設函數為y=a（x+1）²+k，再將點（-2，49），（2，41）帶入到函數中可以算出a=-1，k=50，函數關系式為y=-（x+1）²+50，即y=-x²-2x+49.然后是第二個小問，通過對二次函數進行分析，可以知道函數的開口是向下的，所以函數的最大值是位于函數的對稱軸上，因為a=-1＜0，所以當x=-1時ymax=50.最后是第三問，10天時間的生長高度要大于250mm，那么每天的生長高度就要大于25mm，將這個值帶入到函數關系中就能夠得到溫度的兩個解，從而就能夠得到溫度的區間范圍.

解：（1） 因為函數過（-2，49），（0，49），且（-2，49），（0，49），（2，41）不在同一條直線上，所以函數為關于x=-1對稱的二次函數，設函數為y=a（x+1）²+k，帶入（-2，49），（2，41）可得49=a（-2+1）²+k，41=a（2+1）²+k，所以a=-1，k=50，所以y關于x的函數關系式為：y=-（x+1）²+50，即y=-x²-2x+49.

（2） 由第一小問可得函數關系為y=-x²-2x+49，因為a=-1＜0，所以當x=-1時函數有最大值ymax=50，所以當x=-1時植物每天的生長高度最大.

（3） 植物10天生長的高度總和大于250mm，那么植物每天的生長高度需要大于25mm，將y=25帶入y=-x²-2x+49可得25=-x²-2x+49，

即x²+2x-24=0，所以x₁=-6，x₂=4，又y＞25，則-6＜x＜4.

回顧：數據分析類問題主要就需要通過對數據之間的關系進行分析.本題需要通過數據關系來確定函數關系，需要學生對各種函數的特點有明確的認識，根據函數特點和數據關系來對函數的形式進行確認，從而就能夠對后學的問題進行計算.

7 總結

綜上所述，文章通過例題解析的方式來對數學核心素質進行了探討.通過這些例題可以知道數學核心素養就是數學思想，所以對數學核心素養的培養就是對學生數學思想的培養.所以通過數學思想來對數學問題進行解答是提升學生數學核心素養的關鍵.