初中數學有效教學策略探析

朱春秋

摘 要：在倡導和推行新課程改革的背景下，初中數學有效教學的策略研究為開展數學課堂教學，提升數學教學效率提供了理論基礎，是如今教育教學改革深入發展的一大趨勢，也是廣大教師著重探討的重要課題.本篇內容立足于有效數學教學課堂的基礎，結合數學課堂教學案例，加以淺談初中數學有效教學的基本策略.

關鍵詞：初中數學；有效教學；策略

有效數學教學策略是初中數學教學研究的重要課題之一.它的研究為提升學生數學素養，提高數學課堂質量提供了理論基礎.有效教學要求老師不僅要充分鉆研教材，精準把握數學課堂教學的重難點，還要創設激發學生學習興趣的問題情境，引導學生積極融入數學課堂活動，讓學生主動探究、發現并解決問題，讓學生有意義地學習數學和應用數學.

1 有效數學教學的涵義

20世紀提出的“有效教學”成為廣大教師著重探討和為之不斷追求的教育理念，因此要正確認識有效數學教學.“有效數學教學”是指學生通過參與教師高質量、高效率的課堂教學活動，真正提高自己的數學能力，體驗數學學習的快樂，獲得數學方面的成就感和滿足感.它不是指教師是否完成教學內容，而是要看學生在數學方面有沒有得到實質性的發展與進步.老師在數學課堂盡力講解，學生并沒有認真去學習，沒有收獲實質性的數學知識，也是無效的數學教學.反之，學生認真參與學習，但數學卻沒有取得相應的進步，也稱為無效的數學教學.教師遵循數學教學過程的基本規律，投入最少的精力，去獲取最多的數學教學效益，高效率地完成教學，幫助學生獲得最大的進步與發展也可被稱為“有效教學”.

2 有效數學教學的策略

實行有效數學教學活動任重道遠，有效數學教學不僅要滿足數學教學過程的規律，還要遵循學生身心發展的需要，充分發揮學生在數學課堂的主導作用，讓學生真正參與到數學課堂活動中，獲得相應的進步與發展.可以從以下幾個方面展開：

2.1 有效備課，確立合適的數學教學目標

一位合格的數學老師在教學之前，首先關注的不是學生要學什么樣的內容，而是學完了數學能夠做些什么.因此教師要根據新課改的要求和學生已有的知識基礎及認知能力，運用科學恰當的方法，確立合適的數學教學目標，數學教學活動就有了靈魂和主題，它是初中數學教學活動中至關重要的起點.

義務教育的數學新課標體現了課程的普及性、基礎性和發展性，面向初中生，要使學生必須掌握數學基本知識和基本技能，能夠運用數學觀察、解決生活中常見的問題，使學生了解數學的價值，增強數學的實用性，從而激發學習數學的興趣.人人都能夠學習有價值的數學，人人都能在數學的不同方面獲得不同的發展.

2.2 運用多種教學手段，充分調動學生主觀能動性

隨著時代的發展，學生的興趣愛好廣泛，課堂注意力普遍不集中或者集中時間較短，學習的積極性不高.同時，初中數學在各科目中也是一大難題，是教師“難以授課，學生難以吸收”的課程，課堂難度增加，學生學習困難，導致興趣驟減，教學效果不佳.此時教師需要采用靈活多樣的教學手段，去組織有效數學教學，調動學生學習的積極性.

比如在蘇教版七年級數學中《2.7.1有理數的乘方》一節時，讓孩子“動手折紙”和“大意的國王被象棋發明者拉空了糧倉的故事”吸引孩子注意力，使課堂活力瞬間拉滿，更為簡潔理解乘方的意義；而在蘇科版初二數學《2.1軸對稱與軸對稱圖形》中，采用自己動手操作，小組合作展示的方式，使課堂避免“滿堂灌”的誤區，充分發揮學生的主體性，使學生積極主動參與教學活動中.

因此教師要靈活使用多種教學手段，創設與課堂相關且易激發學生學習興趣的數學情境，使學生以輕松愉悅的狀態，高效地進入數學課堂，有效地參與數學教學活動.

2.3 合理安排教學環節，確保課堂進行有效教學

在實際課堂中，要做到有效教學，有非常重要的兩點內容：首先是要有精確的教學；然后是要有合理的教學環節內容.準確把握學情，對數學課堂進行改進、補充和再創造，以便更為合理的安排教學任務，使之更好地服務教學和學生.

下面是蘇科版初二數學《3.1勾股定理》一課的教學過程.

（1） 創設情境，導入新課

大屏展示：以紀念郵票為情境導入課堂，獨自觀察郵票上各個正方形的小方格的個數，猜想關系.

（2） 合作交流，探究新知

計算分別以直角三角形的三邊組成的三個正方形的面積，小組內合作交流，展示數量關系.

（3） 深化理解，鞏固新知

設計表格，讓學生在方格紙上操作，引導學生猜想正方形的面積與直角三角形三邊長的數量關系，將數據填表，使學生對勾股定理有了深刻的理解.

（4） 強化思想，歸納小結

① 現在你對直角三角形有哪些認識？

② 勾股定理揭示了“形”與“數”的內在聯系，你能從已知的知識舉例嗎？

（5） 分層練習，布置作業

必做題：課后習題第1、2題；選做題：課后習題第3題.

孩子是數學課堂教學的主體，所有的數學教學活動都應以孩子占主導地位.面對有巨大發展潛能和個別差異的學生，教師要合理安排組織教學環節，使每個教學工作環環相扣、相互補充和完善，確保每個環節教學有效.

2.4 靈活設計分層練習，鞏固有效教學效果

教師應以“促進學生發展”為目標，針對不同程度知識與技能的學生，分層布置練習，在準備基本題型的基礎同時，教師也要加強對知識的拓展延伸練習，提高學生“舉一反三”的能力，循序漸進，有效鞏固課堂教學.

比如布置這樣的兩道題時：

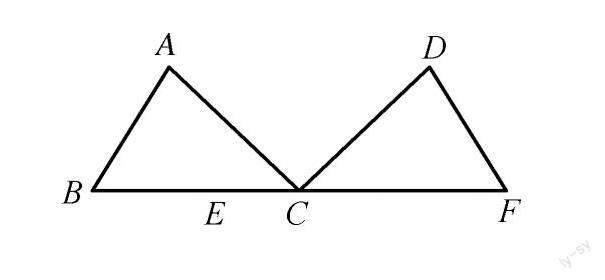
例題 如圖，C點是線段BF的中點，AB＝DF，AC=DC.△ABC和△DFC全等嗎？

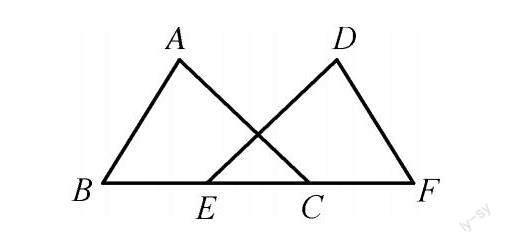
【變式】若將上題中右邊的三角形向左平移（如圖），若AB＝DF，AC=DE，BE=CF.

問：△ABC和△DFE全等嗎？

雖然都是證明三角形全等，但第一題只需直接找出三個條件即可，而第二題需要間接求出BC=EF才可證明，過程稍微麻煩一些.這兩道題是同一類型的題目，并且都在用“邊邊邊”證明三角形全等，但是其中難度層次是不同的.教師在安排練習鞏固時，應根據學生知識掌握的不同情況和水平，依次遞進分層次地布置作業練習，在提升學生自信心的同時，保證課堂教學的有效性.

2.5 同課異構，優化反思有效教學

因為每個教師的數學教學理念不盡相同，針對相同的數學教學內容，采用不同的教學思路和風格，可達到殊途同歸的課堂效果.即使處理教學的方式大同小異，但課堂的呈現方式和應對方式又會迥乎不同.因此教師必須要深入研究學生，設計符合學生身心發展的有效數學教學活動，幫助學生真正理解和掌握所學知識的同時，也可以提升老師的理論水平，促進老師的專業化成長與發展.

“同道而相益，同心而共濟”，教師應認真關注學生“如何主動學，如何學得更好”，進而在平時的教學活動中，時刻思考和及時調整自己的教學理念，在“有效數學教學”的路上，師生雙方行穩致遠、共同發展、共同進步.

參考文獻：

［1］ 常冬琴.“勾股定理（1） ”教學設計及教后反思［J］.數學教學通訊，2020，717（8）：16-18.

［2］ 陳溪.勾股定理的教材編排和課堂教學比較研究——以蘇科版和人教版為例［D］.揚州大學，2020.

［3］ 王亞權.問題引領探究合作促進理解——對“勾股定理”一課的點評［J］.中國數學教育，2020，215（11）：38-39+48.

［4］ 秦瑤.在參與中探尋“生長”的數學課堂［J］.小學生（中旬刊），2019（7）：94.

［5］ 吳增生，鄭燕江，李宏彥，陳婭芬.勾股定理教學實驗研究——讓學生真正經歷勾股定理的“再發現”過程［J］.數學教育學報，2017，26（1）：50-54+75.