初中數(shù)學輔導的有效性策略研究

蔡育偉

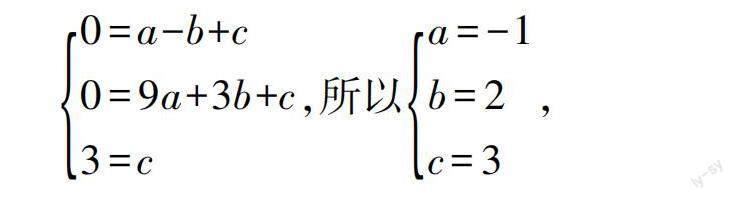
摘 要：隨著數(shù)學知識的深入學習，數(shù)學的學習難度也在逐漸上升.初中階段是學生數(shù)學成績出現(xiàn)分化的重要時期.很多學生無法做到將課堂上所學的數(shù)學知識進行有效的消化，所以就需要教師在課后服務(wù)階段對學生進行輔導，從而將所學的數(shù)學知識進行鞏固.“1+X”課后輔導模式即是立足于課堂教學來進行課外拓展，本文將結(jié)合初中數(shù)學二次函數(shù)的解題輔導來對“1+X”課后輔導模式進行分析，從而提升數(shù)學課后輔導的有效性.

關(guān)鍵詞：初中數(shù)學；課后輔導；學習拓展；“1+X”課后輔導模式

“1+X”課后輔導模式是立足于課堂教學的基礎(chǔ)上，在課后輔導的過程中拓展數(shù)學學習活動.在“1+X”課后輔導模式中，“1”代表的是課堂教學內(nèi)容，“X”則表示的是課后輔導的各種形式和內(nèi)容.一般包括閱讀、實踐以及解題講解等數(shù)學活動方式.下文將結(jié)合二次函數(shù)的解題輔導來對“1+X”課后輔導模式進行說明.

1 試題呈現(xiàn)

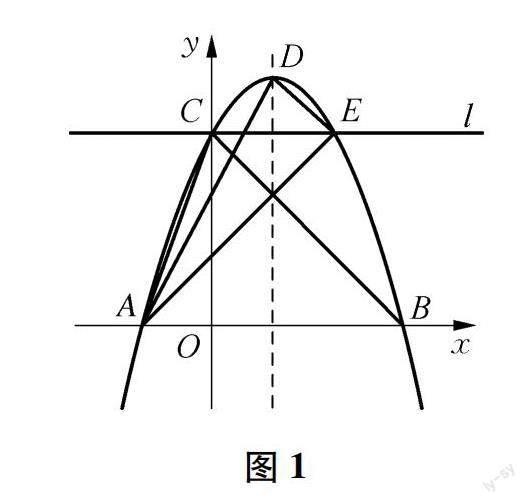
例1 （2022年四川綿陽中考試題24題）如圖1所示，拋物線y=ax²+bx+c交x軸于A（-1，0），B兩點，交y軸于點C（0，3），頂點D的橫坐標為1.

（1） 求拋物線的解析式；

（2） 在y軸的負半軸上是否存在點P使∠APB+∠ACB=180°，若存在，求出點P的坐標，若不存在，則說明理由；

（3） 過點C作直線l與y軸垂直，與拋物線的另一個交點為E，連接AD，AE，DE，在直線l下方的拋物線上是否存在一點M，過點M作MF⊥l，垂足為F，使以M，F(xiàn)，E三點為頂點的三角形與△ADE相似？若存在，求M點的坐標，若不存在，請說明理由.

2 “1+X”課后輔導模式下的數(shù)學試題閱讀

在數(shù)學課后輔導的解題輔導中，需要根據(jù)“1+X”課后輔導模式來讓學生對數(shù)學問題進行閱讀以對試題進行分析.

例如在這道試題中，根據(jù)已知條件拋物線y=ax²+bx+c交x軸于A（-1，0），B兩點，交y軸于點C（0，3），頂點D的橫坐標為1.通過對已知條件的閱讀就可以對拋物線的情況進行分析，根據(jù)拋物線頂點的橫坐標為1，就可以知道拋物線的對稱軸為x=1.然后結(jié)合拋物線交x軸于A（-1，0），B兩點，就可以對B點的坐標進行計算，然后就可以根據(jù)A，B，C三個點的坐標來計算得到關(guān)于拋物線的方程式.

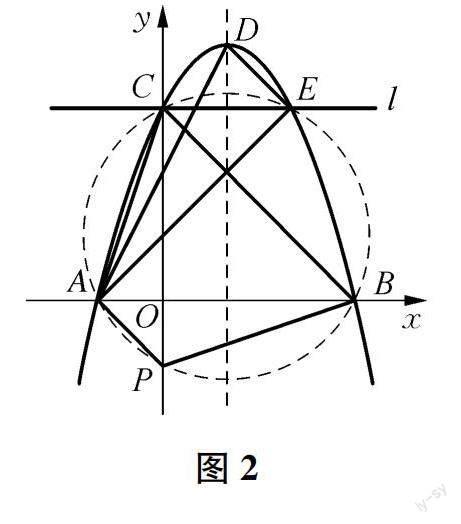
根據(jù)第二小問的題意，在y軸的負半軸上是否存在點P使∠APB+∠ACB=180°，所以這時就可以假設(shè)存在這樣的P點，這樣就可以構(gòu)成一個四邊形，根據(jù)題意∠APB+∠ACB=180°，所以就存在∠CAP+∠CBP=180°，所以就可以得到A，B，C，P是四點共圓的關(guān)系，如圖2所示.然后根據(jù)（1）中關(guān)于B點的坐標計算結(jié)果，就可以得到△OBC為等腰直角三角形，從而就可以知道∠OBC=∠OCB=45°，然后根據(jù)四點共圓四個點連成同側(cè)共底的兩個三角形頂角相等就可以得到∠ABC=∠APC=45°，所以△OAP為等腰直角三角形，所以O(shè)A=OP=1，這樣就可以得到P點的坐標.然后是對第三個問題的閱讀，通過閱讀可以得到如圖3所示的圖象.根據(jù)（1）計算所得到的拋物線解析式以及拋物線的對稱軸就可以對D，E兩點的坐標進行計算，然后根據(jù)兩點之間的距離公式來得到AD，DE，AE的長度，進一步分析就可以得到△ADE是直角三角形，得到這個直角三角形的兩條直角邊的比值關(guān)系，然后根據(jù)相似三角形的性質(zhì)來對三角形EFM的兩條直角邊的比值關(guān)系進行分析，從而得到M點的坐標.

3 “1+X”課后輔導模式下的解題實踐

通過對題目的閱讀分析，后續(xù)進行的就是根據(jù)閱讀分析的結(jié)果來對題目進行解題實踐.通過實踐的方式來判斷自己在閱讀過程中的分析是否正確.

解：（1） 因為拋物線頂點D的橫坐標為1，

所以拋物線的對稱軸為x=1，

又因A（-1，0），

所以B點的坐標為（3，0）；

將A（-1，0），B（3，0），C（0，3）分別帶入到y(tǒng)=ax²+bx+c可得：

所以拋物線的解析式為：y=-x²+2x+3；

（2） 存在這樣的P點，坐標為（0，-1），理由如下：

假設(shè)存在這樣的P點，因為∠APB+∠ACB=180°，

所以∠CAP+∠CBP=180°.

所以A，B，C，P四個點為四點共圓的關(guān)系，如圖2所示，

由（1）可知OB=OC=3，

所以△OBC為等腰直角三角形，即∠OBC=∠OCB=45°，

根據(jù)四點共圓的性質(zhì)可得∠ABC=∠APC=45°，

所以△OPA為等腰直角三角形，

OA=OP=1，

所以P（0，-1）；

（3） 存在這樣的M點，理由如下：

根據(jù)題意可得到圖形如圖3所示，

根據(jù)（1）所得的解析式y(tǒng)=-x²+2x+3以及拋物線的對稱軸為x=1可得：

D，E兩點的坐標分別為D（1，4），E（2，3），

因為A點的坐標為A（-1，0），

因為AD²=DE²+AE²，

所以△ADE為直角三角形，且∠AED=90°且DE∶AE=1∶3，

根據(jù)題意設(shè)點M的坐標為M（t，-t²+2t+3），又因點M在直線l的下方，

所以t的范圍是t＜0或者t＞2，

所以EF=|t-2|，MF=t²-2t，

要讓△MEF與△ADE相似，則需要EF∶MF=1∶3，或者MF∶EF=1∶3，

4 “1+X”課后服務(wù)模式下的講題教學

學生通過自己對例題的閱讀和解答之后，就需要教師對學生進行引導，讓學生利用自己的語言講解對這個例題的理解、解題思路以及思維過程.在這過程中需要讓學生能夠?qū)⒆约簩@個例題的理解清晰地表達出來，然后能夠?qū)@個數(shù)學問題所采用的數(shù)學思維進行說明.通過這樣讓學生對試題進行講解的方式來讓學生在班級或者小組內(nèi)進行講題訓練，從而讓學生加深對這類知識的理解.

例如在這個例題中，求解一個二次函數(shù)的解析式需要將拋物線上的三個點的坐標帶入到二次函數(shù)的一般式中來進行求解，所以需要根據(jù)題意來得到拋物線上的三個點的坐標，所以在求解析式的過程中最關(guān)鍵的一步就是通過拋物線的對稱軸x=1來對拋物線與x軸的交點B點的坐標進行計算，實現(xiàn)對拋物線解析式的求解.而第二個問題則是側(cè)重考查了四點共圓的相關(guān)關(guān)系，通過對角之和為180°的關(guān)系來判斷出A，B，C，P四個點屬于四點共圓的關(guān)系，然后結(jié)合四點共圓中以相同邊AC所作的△ABC與△APC的頂角∠ABC=∠APC，從而通過角的關(guān)系來判斷出邊的關(guān)系，得到P點的坐標.然后是第三個問題，通過對問題的分析可以發(fā)現(xiàn)需要構(gòu)造出一個△EFM與△AED相似.而觀察圖形可以發(fā)現(xiàn)兩個三角形沒有直接的幾何關(guān)系上的聯(lián)系，所以就需要通過直角三角形兩條直角邊的比值相等這個判定方式來對三角形相似進行判定，所以就需要利用△AED的邊長關(guān)系來判定三角形是否為直角三角形，從而確定三角形的直角邊.

通過學生對這個例題的解題思路的講解，可以促進學生對講解過程中存在的一些問題進行進一步的分析和說明，從而使學生加深對這類問題的理解.同時講解完成之后可以根據(jù)這個例題來進行進一步的延伸，對二次函數(shù)中常見的問題進行進一步的講解，使學生對二次函數(shù)問題有更加深入的了解.

5 “1+X”課后輔導模式的有效性分析

數(shù)學學習的過程就是對知識點的學習，然后通過試題來對所學知識進行應(yīng)用，而“1+X”課后輔導模式注重的就是學生在課后輔導解題練習過程中對試題的閱讀、解題實踐以及對試題的講解.在課后練習的過程中通過這樣的輔導模式可以讓學生對所學知識點進行有效的應(yīng)用，通過對試題的仔細閱讀分析，來實現(xiàn)學生對試題的全面剖析，從而找到解決試題的思路和方法，然后通過解題實踐來對自己所尋找到的解題思路和方式進行驗證，來判斷自己的思路和方式是否存在問題.最后通過試題講解的方式來說明和總結(jié)自己對這類問題的理解，從而進一步地提升了對這類問題的掌握程度.這種課后輔導模式有效強化了學生對課堂所學知識的掌握度，使課后輔導的效果得到有效的提升.

6 結(jié) 語

綜上所述，本文通過一道中考數(shù)學二次函數(shù)試題來對“1+X”課后輔導模式應(yīng)用在初中數(shù)學課后輔導中的有效性策略進行了說明.通過“1+X”模式對試題進行閱讀分析、解題實踐、講解思路的方式能夠有效地提升課后輔導過程中的輔導效率，使學生能夠更好地將課堂所學的知識進行有效的應(yīng)用，從而使學生的數(shù)學成績得到穩(wěn)步的提升.

參考文獻：

［1］ 黃啟勇.提高初中數(shù)學課后輔導效率的對策［J］.知識窗，2019（5）：55.

［2］ 陳亮.“雙減”政策下初中數(shù)學課后延伸輔導——提升學生“學力”路徑研究［J］.課程教育研究，2021（15）：114-115.

［3］ 冷經(jīng)偉.利用Q+S教學模式進行初中生數(shù)學課后輔導的實踐研究［D］.遼寧：沈陽師范大學，2018.

［4］ 張新富.新課程背景下的初中數(shù)學有效性策略探析［J］.考試周刊，2017（82）：128.

［5］ 吳成梅.提高初中數(shù)學教學有效性的策略探索［J］.課堂內(nèi)外·初中教研，2022（9）：72-74.