試卷講評的“加分制”策略探究

蔣寶慧

摘 要：試卷講評是教學的重要環節，針對學生在知識方面的漏洞，分析解決問題的欠缺，在試卷講評中通過建立“加分制”策略激發學生獨立糾錯、組內合作糾錯的興趣，教師在此基礎上再進行適當的拓展延伸，達到數學思想方法的引領，真正做到教師“導”，學生“學”，讓數學試卷講評課真正成為發展學生思維、提升學生能力的課堂.

關鍵詞：試卷講評；加分制；策略

試卷講評是指在測試后對試卷進行分析、講解和點評，其目的是找出學生在知識方面的漏洞、理解能力水平方面的欠缺，糾正錯誤，提高分析和解決問題的能力.尤其到了復習階段，試卷講評課更是成為了常態課.本文從學生心理和學習需要兩個方面出發，通過實施“加分制”建構一套可操作且實效性強的試卷講評策略.

1 “加分制”的簡述

每當試卷發下來的時候，學生第一眼看的就是自己的分數，緊接著就是想知道什么原因導致丟分.通過對學生答題的分析，我們發現學生的錯因主要是以下三個方面：（1） 答題態度造成的；（2） 知識點混淆或缺失導致的；（3） 思維障礙，分析和解決問題能力欠缺導致的.對因答題態度和知識缺漏導致的錯誤，基于學生心理需要和學習需要，教師要給學生提供一次獨立改正的機會；因思維障礙，分析和解決問題能力欠缺導致的丟分，可以嘗試通過小組合作來解決，再把兩次糾正后分別獲得的小題分加入總分，給學生提供不斷研錯、糾錯的動力.

2 “加分制”的步驟

第一步：測試后，教師要及時批改試卷，尤其是解答題要按照分步給分，把錯誤的步驟圈出，并標注“？”，讓學生清楚自己哪一步出現了錯誤，以便在訂正環節能快速找出自己丟分的原因，為學生的自主訂正提供了更明確的方向.

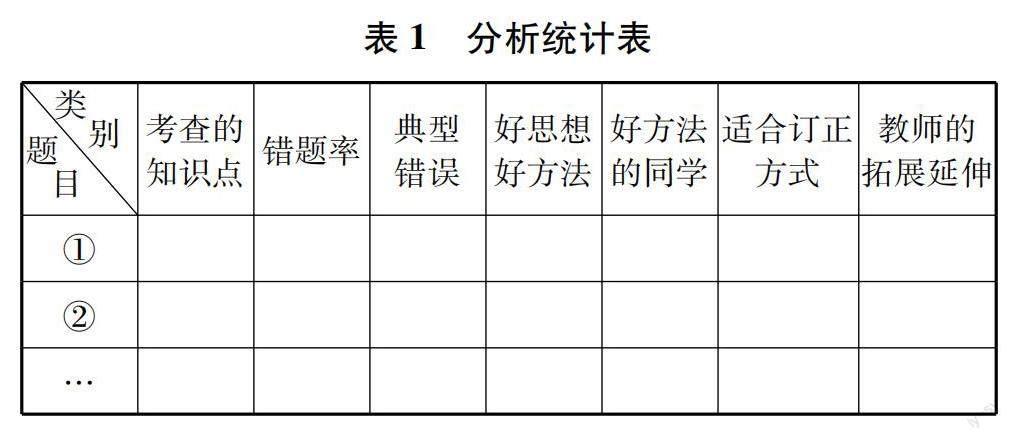
第二步：發放試卷前，可以運用“智學網”“悠數學”等大數據系統幫助統計.細致分析學生答題情況，既要定性分析，又要定量分析.在定性分析中，要對學生答題時的錯誤做認真診斷，是屬于答題態度，還是知識混淆，又或者是分析問題能力欠缺，哪些是典型錯誤，哪些同學的解題方法、解題思路好等等都要做出定量分析，并對哪些題學生可以自己解決，哪些題需要教師講評等做好預估，并制成表格.

第三步：試卷發下去后，利用考試后的第一節課前半段時間讓學生進行獨立訂正，訂正正確加上小題分.獨立訂正無法解決的問題，可以在這節課的后半段時間進行組內合作講解，訂正正確同樣可以加上小題分.

第四步：針對組內講解仍無法解決的問題，教師利用考試后的第二節課進行詳細講評，并適當拓展延伸.

3 “加分制”的具體實施

3.1 獨立自主，糾正基礎錯誤

試卷發放后，教師要給學生搭建獨立訂正的平臺，組織學生針對試卷答題中因答題態度和知識缺漏出現的錯誤進行訂正，此環節需要做好“一公二定三加”：一是教師公布答案，學生針對因知識缺漏而出錯的試題進行訂正時，可以查閱教材或相關資料；二是教師要制定規則，防止學生不求甚解，直接填寫一個答案了事.學生必須說明本題錯誤原因，然后再寫出詳細的解答過程；三是及時加分，即把學生獨立訂正所獲得的分值及時加入原始成績，作為學生考試后的再次得分，以此激勵學生保持訂正的熱情.

獨立訂正實效性：獨立訂正環節后，教師會看到每一份試卷上對錯題的自我剖析，如：“呀，我怎么沒看到這個條件？我要是圈關鍵詞就不會錯了！”再如：“我怎么能記錯這個公式呢？難道我考前記得的公式是假的啊？”“我真應該把書好好看看！”.看到這些略帶自嘲的語言，我覺得孩子們可愛的同時，也更加堅定了為孩子們提供一次自我糾錯加入考分的機會，認識到細心答題的重要性，使其學習態度在自我糾錯中得到修正.針對考試中因知識缺漏而出錯的試題，給學生一次翻閱教材或參考資料進行糾錯后加入考分的機會，讓其對教材或學習資料中的數學法則、數學公式、數學定理、數學概念及相關性質進行閱讀，厘清知識，同時，使自主學習的習慣和能力均得到有效地培養.

3.2 組內互助，擴展解題思路

試卷批改后，根據學生的答題情況，按照“組內異質，組間同質”原則對學生進行分組，同時，對小組長進行培養，使小組長起到“小老師”的作用.每組成員既要考慮成績高低的搭配，又要考慮思維活躍性的互補，為糾錯時能夠積極討論做好準備.學生在自我訂正環節未能解決的問題，可以在小組長的帶領下，充分地交流討論，不僅能互相糾錯，還可以讓方法進一步優化.組內合作糾錯時，為避免小組長因講解不清而直接把解答過程提供給組員，教師要提前對各組長進行糾錯輔導.要有知識點的講解，更要有糾錯方法的指導；要敢講，更要思考如何講，最終達到讓組員真正理解.經過小組合作糾錯后，學生能說明自己的錯誤原因，并能寫出詳細的解答過程，同時解題思路也得到了進一步的擴展.

組內互助實效性：各小組合作糾錯時，教師可以在小組間來回巡視，發現問題時可以作為“親友團”及時支援，提高糾錯效率.這樣也避免了組員直接抄答案的情況，不讓加分流于形式，要在合作學習中進行知識的互補及解題能力的共同提升，使團隊成員的合作學習興趣得以激發與培養，合作學習習慣得以養成，合作學習方法得以建構，合作學習能力得以不斷訓練和發展，也就達成了我們組內互助環節的基本目標.實踐一段時間后，根據暴露出來的問題，教師分析原因，可以對組員進行優化調整，進一步提高組內互助的功能.

3.3 教師引領，體會數學思想

經歷了學生獨立糾錯和組內互助糾錯環節，教師需要講評的題目不在多而在精，切記教師不能僅僅就題講題，一定要強調試題如何分析，訓練學生審題并快速準確找到解題思路的切入點，可以在原問題基礎上，進行適當地拓展延伸，以找到解決這一類問題的通法.這一環節，教師課前要做到“一關二研三建”：一要關注前兩個環節的反饋，進行適當補充或調整；二要研判學生的思維障礙點，進行合理設計問題；三要聚焦問題考查的數學思想，尋找解決這一類問題的通法.

3.4 數學卷講評課

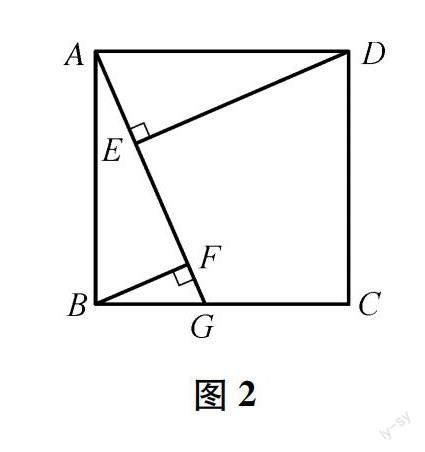
例1 如圖2，四邊形ABCD是正方形，點G是BC上一點，DE⊥AG于E，BF⊥AG于F，求證：DE=BF+EF.

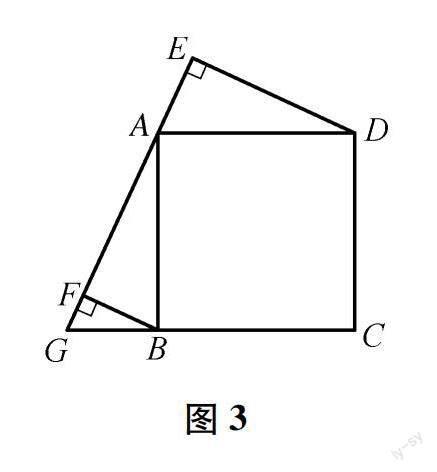
例2 如圖3，當點G在CB的延長線上時，其它不變，探求BF，DE，EF的關系.

【講解說明】例1、例2的共性是：根據“三垂直模型”，易證∠BAF=∠ADE，從而根據“角角邊”可證△ABF≌△DAE，得到DE=AF，AE=BF，只是最后的結論略有不同，但本質相同.這兩小題學生的得分率較高，無需贅述.

例3 如圖4，點P是正方形ABCD內一點，PB=5，S_△PAB=10，S_△PBC=5，求S_正ABCD.

【思維障礙分析】本題學生的困惑在于不知如何把條件中兩個三角形的面積與正方形邊長聯系起來.

障礙1：表示S_△PAB和S_△PBC時，習慣性把AB、BC看做底邊，忽略了PB=5這個條件，導致無法求解；

障礙2：在略有變化的圖4中沒有發現“三垂直模型”，忘了“變中找不變”.

因此，教師講評的關鍵就是加強思維點撥，引導學生進行問題分析以快速找到解決問題的思維切入點.當學生知道如何添加輔助線，并能發現數學模型時，計算問題就交由學生了.

【思路點撥】

問題1：由PB=5，S_△PAB=10，你能得出什么？

由PB=5，S_△PBC=5，你又能得出什么？

問題2：在圖4中，你能構造出與前兩小題不變的模型嗎？

問題3：要想得S_正ABCD，就需要求出什么？

問題4：根據問題1得出的AE、CF的長，如何求出正方形的邊長？

有了問題串的引導，再根據前兩小題積累的經驗，此題就不難解決了.

教師講評實效性：在例3講解過程中，教師不僅進行了思維障礙的分析，還通過設計層層遞進的問題，把條件逐一轉化，從變化的條件中尋找不變的數學模型思想；例4體現了更一般化的方法和結論，變化的是：由正方形變為了長方形，解題過程中的全等三角形變為了相似三角形，對應邊相等變為了對應邊成比例，而“三垂直模型”始終沒有變，讓學生進一步體會到變中有不變，并針對問題解答中所運用的“轉化”“模型”等常用數學思想方法進行系統建構.通過逐級推進的講評活動，不僅學生的數學糾錯思維得到了有效的指導和訓練，學生的數學運算、數據分析、邏輯推理、數學建模等素養也得到了發展和提升.

試卷講評是教學的重要環節，教師應改變“逐題講解，就題論題，一講到底”的做法，要積極搭建學生能夠參與的平臺，培養生生、師生之間的合作意識，真正做到教師“導”，學生“學”，讓數學試卷講評課真正成為發展學生思維、提升學生能力的課堂.