分類討論思想在數(shù)學(xué)解題中的應(yīng)用

董文峰

摘 要：分類討論思想作為數(shù)學(xué)中的一種重要的思想，在數(shù)學(xué)解題中有著廣泛而深刻的應(yīng)用.學(xué)生們?nèi)绾巫匀绲剡\(yùn)用這一思想開啟解決問(wèn)題的大門，這是學(xué)生們學(xué)習(xí)的難點(diǎn)，也是教師在教學(xué)中需要重點(diǎn)指導(dǎo)的地方.下面以二次函數(shù)中的圖形存在性問(wèn)題為例，具體講解如何運(yùn)用分類討論思想解題.

關(guān)鍵詞：分類討論思想；二次函數(shù)；圖形；存在性

1 分類討論思想概述

在研究和解決數(shù)學(xué)問(wèn)題時(shí)，當(dāng)不能對(duì)問(wèn)題所給對(duì)象進(jìn)行統(tǒng)一研究時(shí)，把所有研究的問(wèn)題根據(jù)數(shù)學(xué)對(duì)象的本質(zhì)屬性的相同點(diǎn)和不同點(diǎn)分成若干類，轉(zhuǎn)化成若干個(gè)小問(wèn)題來(lái)解決，最后綜合各類結(jié)果得到整個(gè)問(wèn)題的答案，這種解決問(wèn)題的數(shù)學(xué)思想稱為分類討論思想.

分類討論有著特定的產(chǎn)生因素，在初中階段，引起分類討論的主要因素有：（1） 代數(shù)方面：① 由數(shù)學(xué)概念引起的分類討論，如絕對(duì)值定義、實(shí)數(shù)、函數(shù)的定義等；② 由代數(shù)運(yùn)算性質(zhì)引起的分類討論，如算術(shù)平方根的非負(fù)性，含參數(shù)的不等式、方程的求解等；③ 由性質(zhì)、定理、公式的限制引起的分類討論，如二次項(xiàng)系數(shù)的正負(fù)對(duì)二次函數(shù)圖象的開口方向的影響.（2） 幾何方面：① 由幾何圖形中點(diǎn)、線、面的相對(duì)位置不確定引起的分類討論，如直線與圓的位置關(guān)系；② 由幾何圖形的相對(duì)形狀不確定引起的分類討論，如直角三角形和等腰三角形中的邊角的討論.（3） 由實(shí)際問(wèn)題引起的分類討論，如排列問(wèn)題，實(shí)際應(yīng)用題等.（4） 其他方面，如題設(shè)本身有分類，或解題過(guò)程不能統(tǒng)一敘述，必須分類討論的.

運(yùn)用分類討論思想解決這些數(shù)學(xué)問(wèn)題時(shí)通常的步驟為：（1） 明確討論的對(duì)象和范圍；（2） 確定分類的標(biāo)準(zhǔn)，恰當(dāng)?shù)貙?duì)全體對(duì)象進(jìn)行合理的分類；（3） 對(duì)每一類進(jìn)行分析和解決問(wèn)題；（4） 綜合各類的結(jié)果，歸納得出結(jié)論.需要重點(diǎn)強(qiáng)調(diào)的是，第（2）步中的分類是分類討論思想的核心環(huán)節(jié)，關(guān)系到問(wèn)題解決的成敗.在分類時(shí)我們要把握好這四個(gè)原則：（1） 確定性原則，分類的對(duì)象是確定的；（2） 同一性原則，分類是按照同一個(gè)標(biāo)準(zhǔn)進(jìn)行的；（3） 互斥性原則，分類的標(biāo)準(zhǔn)是統(tǒng)一的，分類的各層之間既沒(méi)有重復(fù)的部分，也沒(méi)有遺漏的部分；（4） 層次性原則，根據(jù)題目的特點(diǎn)和要求科學(xué)地劃分標(biāo)準(zhǔn)，大分類中含有小分類時(shí)，要分清主次，不越級(jí)討論.

分類討論思想是一種重要的數(shù)學(xué)思想，在初中的各個(gè)知識(shí)板塊中均有滲透，涉及的知識(shí)面廣，綜合性強(qiáng)，思考容量大，在解題中有著深刻而廣泛的應(yīng)用，有利于培養(yǎng)學(xué)生的有序思考方法、嚴(yán)謹(jǐn)?shù)倪壿嬎季S能力、綜合分析問(wèn)題和解決問(wèn)題的能力.下面就二次函數(shù)中的圖形存在性問(wèn)題中滲透的分類討論思想進(jìn)行具體剖析.

2 分類討論思想在解決二次函數(shù)的圖形存在性問(wèn)題中的應(yīng)用

研究以二次函數(shù)為背景的圖形時(shí)，由于其依托于二次函數(shù)，所以既與函數(shù)圖象有一定的關(guān)聯(lián)性，又有其本身的獨(dú)特性質(zhì).而分類討論思想的運(yùn)用，也正是由圖形的獨(dú)特性引起的.在初中階段，二次函數(shù)主要與直線、三角形、四邊形和圓這些幾何圖形融合在一起進(jìn)行考查，屬于二次函數(shù)的綜合題通常以壓軸題的形式出現(xiàn).其中存在性問(wèn)題主要與直角三角形、等腰三角形、相似三角形、平行四邊形、矩形、菱形和正方形有關(guān)，討論這些圖形在二次函數(shù)中是否存在，通常是由幾何圖形的相對(duì)位置或相對(duì)形狀的不確定性引起的分類討論.

2.1 分類討論應(yīng)用于解決直角三角形存在性問(wèn)題

由于直角三角形的直角特殊性和直角頂點(diǎn)的不確定性，在假設(shè)二次函數(shù)中的直角三角形存在的前提下，則圍繞著直角頂點(diǎn)的位置進(jìn)行分類討論.一般的解法是先把三角形的三個(gè)頂點(diǎn)的坐標(biāo)表示出來(lái)，有的點(diǎn)是用含變量的代數(shù)式表示，有的點(diǎn)是已知點(diǎn)；再用兩點(diǎn)間的距離公式表示出三角形各邊的長(zhǎng)度；然后根據(jù)直角頂點(diǎn)的位置分類，對(duì)每一類情況分別用勾股定理列方程進(jìn)行計(jì)算；最后整理、綜合各類的結(jié)果，得出完整的答案.

例1 如圖1，在平面直角坐標(biāo)系xOy中，已知拋物線y＝ax²+bx+c與x軸交于A（-3，0），B（1，0）兩點(diǎn)，與y軸交于點(diǎn)C（0，3），連接AC，點(diǎn)P為第二象限拋物線上的動(dòng)點(diǎn).

（1） 求a、b、c的值；

（2） 連接PA、PC、AC，求△PAC面積的最大值；

（3） 在拋物線的對(duì)稱軸上是否存在一點(diǎn)Q，使得△QAC為直角三角形，若存在，請(qǐng)求出所有符合條件的點(diǎn)Q的坐標(biāo)；若不存在，請(qǐng)說(shuō)明理由.

思路分析：（1） 用待定系數(shù)法即可得出結(jié)論；（2） 先求出直線AC的解析式，設(shè)出點(diǎn)P坐標(biāo)，表示出點(diǎn)Q坐標(biāo)，再用三角形的面積公式，得出函數(shù)關(guān)系式，即可得出結(jié)論；

（3） 運(yùn)用配方法求出拋物線對(duì)稱軸，設(shè)點(diǎn)Q（-1，n），根據(jù)A（-3，0），C（0，3），可運(yùn)用勾股定理分別求出AC²，CQ²，AQ²，由于△QAC為直角三角形，可以分三種情況：∠CAQ＝90°或∠ACQ＝90°或∠AQC＝90°，對(duì)每種情況運(yùn)用勾股定理列方程求解即可.

2.2 分類討論應(yīng)用于解決等腰三角形存在性問(wèn)題

探究等腰三角形的存在性問(wèn)題時(shí)，在假設(shè)其存在的前提下，充分利用題目的已知條件，把與等腰三角形有關(guān)的點(diǎn)和邊求出來(lái)，然后按照哪條邊是等腰三角形的底邊進(jìn)行分類，對(duì)每一類情況，充分利用等腰三角形的性質(zhì)，如兩腰相等，底邊上的中線垂直平分底邊等，展開求解，最后綜合各類結(jié)果，得出答案.

例2 已知拋物線y＝x²+bx+c（b，c為常數(shù)）交x軸于點(diǎn)A（1，0）和點(diǎn)B，交y軸于點(diǎn)C（0，5），拋物線的對(duì)稱軸與x軸交于點(diǎn)D.

（1） 求該拋物線的解析式；

（2） 在y軸上是否存在一點(diǎn)P，使△PBC為等腰三角形，若存在，請(qǐng)求出點(diǎn)P的坐標(biāo)；若不存在，請(qǐng)說(shuō)明理由.

思路分析：（1） 用待定系數(shù)法求出拋物線的解析式；（2） 先求出B點(diǎn)的坐標(biāo)，則BC邊是已知的，要使△PBC為等腰三角形，分別存在三種情況：以BC為底邊或以PB為底邊或以PC為底邊.再結(jié)合已知的BC邊和充分利用等腰三角形的性質(zhì)，即可得出答案.

解：（1） 拋物線的解析式為y＝x²-6x+5；

（2） 存在，理由如下：

如圖3，在拋物線y＝x²-6x+5中，令y＝0，則x²-6x+5＝0，

解得x₁＝1，x₂＝5，∴B（5，0），

∵△PBC為等腰三角形，

∴可分為三種情況：以BC為底邊或以PB為底邊或以PC為底邊.

2.3 分類討論應(yīng)用于解決四邊形存在性問(wèn)題

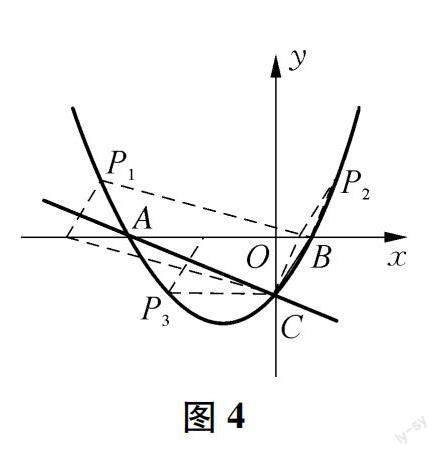
在探討二次函數(shù)中的四邊形存在性問(wèn)題時(shí)，其中的四邊形包括平行四邊形、矩形、菱形、正方形，都在出題的范圍內(nèi)，解決問(wèn)題的關(guān)鍵是在熟練掌握這些特殊四邊形的性質(zhì)和判定的基礎(chǔ)上根據(jù)具體的題目條件，找準(zhǔn)解題的突破口.如在探究平行四邊形的存在性問(wèn)題時(shí)，首先假設(shè)結(jié)論成立，再根據(jù)題中的條件確定已知的平行四邊形的頂點(diǎn)，一般至少已知兩個(gè)頂點(diǎn)，也即是一條邊，而第三、四個(gè)點(diǎn)跟拋物線或者坐標(biāo)軸有某種關(guān)聯(lián)性.已知的這條邊既可以是平行四邊形的一邊，也可以是其中的一條對(duì)角線，由此引起了分類討論.然后針對(duì)每一個(gè)分類情況，充分利用平行四邊形的性質(zhì)和拋物線的性質(zhì)建立關(guān)系式，聯(lián)立方程求解，最后綜合所得的結(jié)果.

在解決二次函數(shù)中的圖形存在性問(wèn)題時(shí)，在對(duì)每一種圖形的探討、分析和解決的過(guò)程中無(wú)不滲透著分類討論的方法和思想，分類討論思想就像是一把解決問(wèn)題的利器，起著決定性的作用.基于圖形的幾何特征

以及在坐標(biāo)系中的位置，首先明確討論的對(duì)象是這些特殊的圖形，如直角三角形；然后再進(jìn)行合理的分類，如等腰三角形是根據(jù)底邊的位置來(lái)分類的，再對(duì)每一情形分別求解，由于是以二次函數(shù)為背景的題型，所以一般求解的是點(diǎn)的坐標(biāo)，最后綜合所得的結(jié)果.

3 關(guān)于分類討論思想的解題教學(xué)建議

從以上的例題可以看出，分類討論不是空穴來(lái)風(fēng)，當(dāng)問(wèn)題的解決路徑產(chǎn)生了分歧時(shí)，分類討論是必然的結(jié)果.

為了讓學(xué)生們?cè)诮忸}中順利地運(yùn)用分類討論思想，在解題教學(xué)中首先要培養(yǎng)學(xué)生們分類討論的意識(shí)，讓學(xué)生有分類討論思想的基本概念.學(xué)而后行，行而后悟，只有讓學(xué)生對(duì)這一思想方法有了初步的認(rèn)識(shí)，才能在解題中嘗試著運(yùn)用.教師可以以一種小專題的形式介紹分類討論思想及其在解題中的運(yùn)用.

其次，指導(dǎo)學(xué)生在各類問(wèn)題中合理地進(jìn)行分類.在全面了解問(wèn)題的解決方式后，按照分類的原則，做到不重不漏地進(jìn)行分類.

最后把握分類討論的嚴(yán)密性和語(yǔ)言表達(dá)的準(zhǔn)確性，分類討論有其基本的步驟，要一步一步地來(lái)，先分述后綜合.

總之，分類討論思想的基本策略是先化整為零，再各個(gè)擊破，最后積零為整.在解題教學(xué)中，需要幫助學(xué)生積累一些分類的方法與技巧，針對(duì)具體問(wèn)題靈活分析和解決，這對(duì)發(fā)展學(xué)生的邏輯思維、綜合和概括能力、探索與應(yīng)用能力大有裨益.