非均質推進劑燃燒演化模擬:算法與驗證

張晏榕,倉 宇,楊 碩,趙 瑜,李坤霖,王利坡

(1.上海交通大學 密西根學院,上海 200240;2.上海航天化工應用研究所,上海 201109)

引 言

固體燃料燃燒問題對于基礎研究和工程應用都十分重要。該問題的復雜性體現在多物理過程的耦合,包括氣相燃燒、固相熱傳導、固相結構的表征以及氣-固界面的質量能量與動量交換。

由于固體燃料使用安全、能量密度高并且成本較低而被固體火箭發動機廣泛使用[1],其中氧化物顆粒高氯酸胺(AP)與聚合黏合劑端羥基聚丁二烯(HTPB)是一種常見的組合。在自維持燃燒開始后,由氣相化學反應產生的熱量導致固相燃料的分解,進而為氣相反應提供反應物。這種雙向耦合決定了界面的溫度以及界面退移速率等條件。

固體燃料燃燒過程涉及多尺度,如何有效模擬不同尺度相關的子過程引起了該領域學者的廣泛關注。與傳統的實驗試錯方法相比,高質量的數值模擬對于設計及預測燃燒行為更為先進和可靠。早期研究通常是利用一維模型或一些統計平均信息。Beckstead等[2]發展了基于統計平均氧化物顆粒的AP混合物燃燒模型。而后Beckstead等[3]展示了混合推進劑火焰的總體結構,包括預混單質火焰、基本擴散火焰以及最終擴散火焰等不同部分,并指出不同火焰之間的相互作用對于理解燃燒過程的重要性,并且也討論了壓強對于火焰結構的影響。Cohen和Strand[4]結合改進的AP單質模型考慮了黏合劑部分的能量守恒關系,并對黏合劑的退移速率模型進行修正。為捕捉更多的物理細節,高維真實的仿真計算不可或缺。Miccio[5]提出一個使用五步化學反應的二維數值計算模型,其中推進劑的幾何特征由表面拓撲掃描決定。Hegab等[6]基于周期性邊界條件的三明治構型做了數值計算并討論不同參數對火焰傳播速度的影響。Jackson和Buckmaster[7]首次對AP和HTPB的混合燃料進行了三維模擬,實現了材料微觀結構的表征以及氣固兩相的共軛傳熱等真實物理現象。此外,Jackson和Buckmaster還考慮氣相與固相的強耦合以解決界面的非穩態且不均勻的退移過程[8]。Massa等采用類似的方法通過映射貼體網格到規則的笛卡爾網格來解決三維界面不規則的問題[9-10]。 Buckmaster研究非均質推進劑燃燒關于壓強擾動的響應[11]。對推進劑微尺度結構的有效刻畫使得結構非均質性對燃燒過程的定量影響成為可能[12]。更全面的非均質推進劑燃燒建模綜述討論可以參考文獻[13]。

本研究提出一種基于重疊網格的非均質固體推進劑燃燒三維模擬框架。該計算框架避免整體求解包含氣固兩相的強耦合方程組,采用分離式的數值求解框架,具體而言,標準笛卡爾網格用于離散氣相以保證計算穩定性,非結構化四面體網格對固相進行離散以更加精準地刻畫由隨機填充算法生成AP粒子結構。兩套網格在計算過程中都是固定的,無需網格重建,所以有利于計算效率和數值準確性。另外水平集方法因其在處理不規則幾何上的靈活性而被采用來有效地追蹤氣-固界面的演化退移。對于浸沒在笛卡爾網格中的邊界單元,可以通過施加源項以滿足氣相的質量、組分和能量的守恒條件。該套計算框架所有功能的集成基于開源平臺OpenFOAM[1]構建。從數值上考慮,算法實現清晰便捷,對于不同邊界條件都可以兼容處理,可為進一步利用數值模擬研究該類問題提供基礎。

1 控制方程和氣-固耦合條件

1.1 氣相

三維低馬赫數帶化學反應的變密度流動由以下連續性方程、動量方程、組分方程以及能量方程來描述,下標“g”和“c”將分別表示氣相和固相:

(1)

(2)

(3)

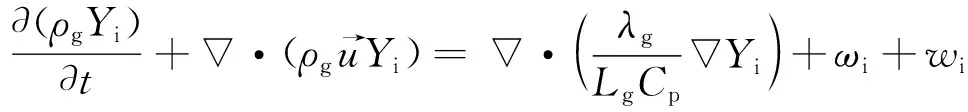
(4)

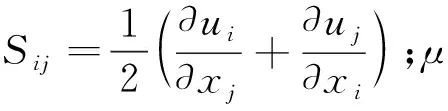
λg=1.08×10-4T+0.0133

(5)

Prandtl數和Lewis數假定為1,采用如下理想氣體狀態方程:

p0=ρgRT∑YiMWi

(6)

式中:背壓p0設定為均一定值(由于低馬赫數流動條件);理想氣體常數R=8.314J/(mol·K);MWi表示i組分的摩爾質量。

1.2 固相

固相的異質形態是復合推進劑燃燒中具有挑戰性的問題,退移速度和燃料的分解過程這些燃燒過程中的物理現象包括很大程度上由固體結構的異質性決定。模擬這種微尺度結構通常需要隨機填充算法[14-15]。固相中的溫度方程如下:

(7)

式中:密度ρc、比熱容Cp和熱導率λc根據該點處于AP內還是HTPB內進行取值。

1.3 氣固界面的邊界條件

固相氣化為氣相提供了質量、動量和能量的源項;與此同時,高溫的氣體也作用于氣固界面進而影響固相內溫度。這種耦合的數值精度對整個燃燒演化過程影響很大。

(8)

φt-rb|φ|=0

(9)

根據熱裂解關系[16-17]:

(10)

式中:TAP,s、TB,s分別表示界面上AP和黏合劑HTPB的溫度。在具體實施中,只有比較大的AP顆粒可以被建模求解,過小AP顆粒被均一地加入到黏合劑中。在這種情況下,根據Chen等的分析,混合材料的退移速率可以表示為[18]:

(11)

式中:α表示作為均質加入黏合劑中AP的體積分數。本研究中相關的參數見表1。

表1 計算所取參數值[8,10,16]Table 1 The parameter values used in calculation[8,10,16]

氣固界面需要滿足如下的溫度連續熱流相等的邊界條件,

Tg=Tc

(12)

(13)

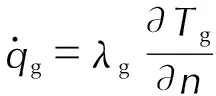
1.4 化學反應

為提高計算效率并且不影響過多的真實燃燒物理現象,本研究采用了已有文獻的簡化全局化學動力學[2,13],具體包含界面和氣相反應的機理[9]。其中界面氣化反應包括:

如果化學反應放熱,此處Qs,1(2)為正值。由于實際界面反應異常復雜(物理、化學參數的確定及凝聚相影響等),該兩步機理是對各種因素的總體體現。

熱分解定律可以衡量氣化的質量流量

(14)

式中:Ac為反應常數;ρc為固相密度;Ec為反應活化能;c為AP/HTPB;Ts為界面溫度。

氣相反應包括:

式中:βs為化學計量參數,類似地,βs在放熱反應中為正值。相應的化學反應速率為:

(15)

式中:Di(i取1,2,3)為反應常數。這3個氣相反應對應了3個不同的火焰[9]: R1對應單質推進劑火焰,R2對應基本擴散火焰,R3對應最終擴散火焰。

2 數值計算方法

在本研究中氣相和固相的計算采用了兩套獨立重疊的網格。對于氣相使用均一的笛卡爾網格,固相采用非結構的四面體網格以刻畫非均質結構。采用Lubachevsky-Stillinger算法生成雙球混合結構[18-19]。圖1展示的填充結構是基于Miller研究中縮寫為M24的SD-III-24[21]算例,紅球和藍球分別代表了直徑為197.6μm和49.4μm的AP粒子,小顆粒被均勻添加到黏合劑中。

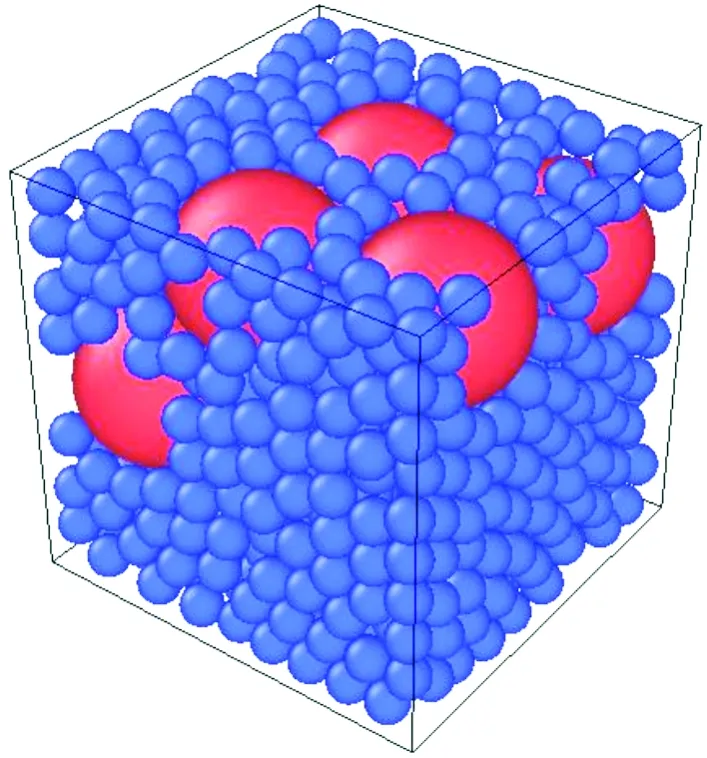
圖1 M24填充模型示意圖Fig.1 Schematic diagram of M24 filling model

2.1 氣相和固相

氣相使用投影法求解壓強泊松方程,耦合處理連續性方程和動量方程[20-21]。化學反應放熱帶來的效果采用Pierce提出的迭代法以實現[24]。具體算法流程如下:

使用Φ=(Yi,T)表示標量,在時間步從tn推進到tn+1過程中首先進入序號為l的內循環。

第一步:在時間步tn中的每一個內循環步l使用以下初始猜測值:

(ρui)0,l=0=(ρui)n

(16)

(ρΦ)0,l=0=(ρΦ)n

(17)

ρ0=2ρn-ρn-1

(18)

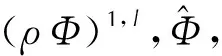
(19)

第四步:根據更新后的密度ρ1,l更新Φ,表示如下:

Φ1,l=(ρΦ)1,l/ρ1,l

(20)

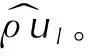
第六步:通過解泊松方程對壓強進行修正:

(21)

第七步:更新速度和壓強:

(22)

(23)

p1,l=p0,l+δp

(24)

重新進行第二步,重復內循環直至達到預設步數。通常在時間步從tn推進到tn+1中采用3次內循環l=0, 1, 2。這些循環完成后,對化學反應求解以更新組分和能量源項,之后時間步從tn推進到tn+1。在以上過程中,空間離散采用基于體心定義的有限體積法,對流項使用多維限制器(MLP)[23-24],方程中其他項使用中心差分。

由于氣相固相網格重疊,該算法需要對浸沒在固相的氣相網格添加限制,具體如下:

ρg=const,ρgΦ=const

(25)

(26)

對于固相控制方程[式(7)]的空間離散選用有限體積法,時間上采用后向歐拉法。氣相的時間推進使用龍格庫塔法[27]。

2.2 界面條件

氣固界面追蹤對于固體推進劑燃燒尤為重要。圖2網格展示浸沒邊界法[3]中的網格區分。粗線表示氣固界面,在粗線以下為固相,以上為氣相。如果一個網格的體心在氣相/固相中,那么就定義這個網格為氣相/固相網格。賦予源項的邊界網格定義在氣固相之間,并且體心處于氣相內的網格。網格中藍色、棕色和紅色分別代表氣相、固相和浸沒被賦予源項的邊界網格。

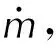
(27)

式中:ρs為固相密度;V為氣相網格的體積。

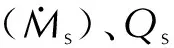
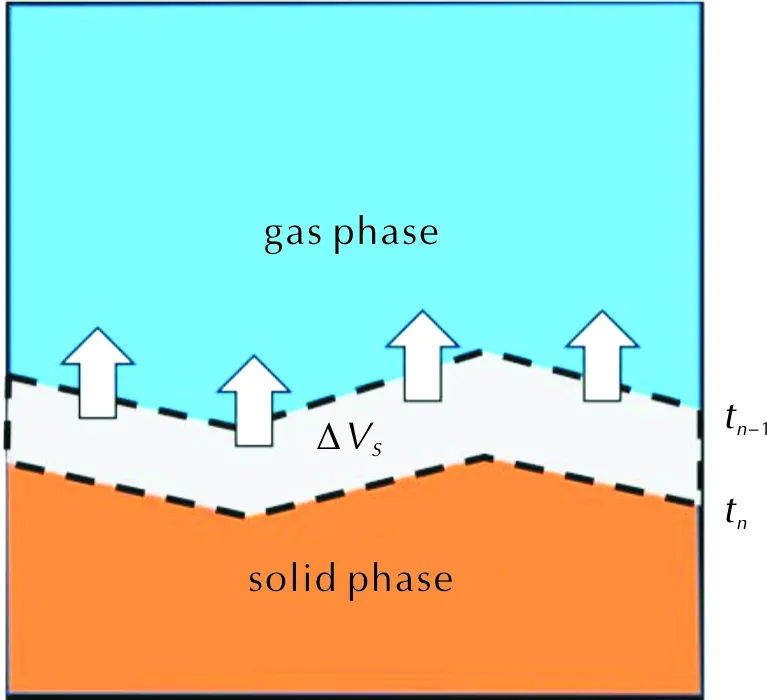
圖3 一個源項網格中通過兩個連續時間步水平集劃分的界面計算Fig.3 Interface calculation of in one source term grid identified by two consecutive time steps level

(28)

數值上,水平集界面追蹤通過顯示正系數法求解式(8)[28]。對于大量非結構化網格,本研究采用快速并行求解器,包括窄帶快速迭代法[29]和補丁窄帶法[30]以分別計算式(9)中的距離變換及界面演化。

燃燒界面上的溫度十分關鍵,本研究通過非迭代的方式對式(13)進行離散求解[31]。在每個時間步,代表氣固界面的等值面φ等于0被顯式插值構建,在固相的非結構化網格中進行這種幾何操作會生成三角形和四邊形單元,如圖4所示,每個單元會被分配到由各自臨近格點組成的在氣固相之間的控制體積內。基于節點的格林高斯公式由于其在高斜網格情況下具有較好的魯棒性被用來離散溫度梯度。界面溫度通過對包括每個界面單元的線性稀疏矩陣進行非迭代求解獲得。這套求解方式被證明擁有二階精度[31]。

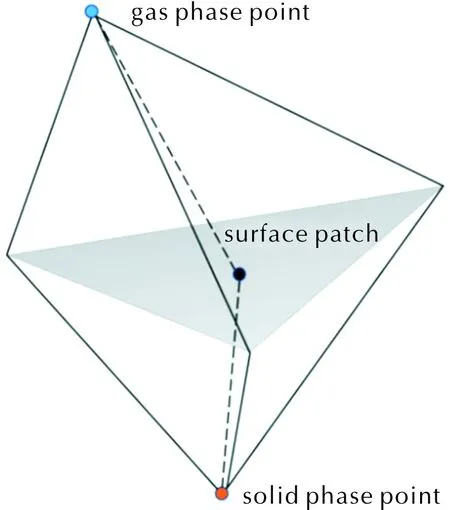
圖4 為計算界面溫度構建的控制體積Fig.4 Control volumes constructed for interface temperature calculation

3 結果與討論

如圖1所示,本研究選用Miller實驗中基于AP的M21和M24推進劑[21]以驗證本套算法。與實驗的壓強范圍一致,選取從0.69MPa到20.7MPa的壓強以研究基于仿真計算的燃速。

對于氣相,計算域尺寸在x,y,z的3個方向上分別為500、500、1000μm。使用均一大小50×50×100的笛卡爾網格,每個網格的尺寸為10μm。速度邊界條件在計算域底部被設置為無滑移,頂部選用零梯度,側面選取滑移條件。壓強在出口設置為定值條件。對于標量(組分和溫度),所有邊界條件均為零梯度。

對于固相,本研究在尺寸為500μm的計算域中生成了13.5萬個非結構網格單元。溫度在底部被設置為定溫300K,側面為絕熱條件。頂部邊界隨著水平集捕捉的氣固界面進行演化并由氣固兩相間的耦合條件確定。

如圖5(a)所示壓強6.89MPa條件下時間演化到0.01s的M24構型溫度場。由于非均勻的局部退移速率,與真實物理過程一致,氣固界面變得扭曲。在氣相場中,最高溫度達到約3200K。從流場中可以發現溫度與速度的相互作用,圖5(b)為相同設置下M24構型的溫度云圖及流線圖。為了更清楚地展示等值面,只顯示出在x方向上一半的等值面。在氣固界面附近,速度方向在局部與界面垂直。界面的不規則性也導致了速度方向和大小的強烈變化。遠離界面,流場受界面的影響逐漸變弱,速度方向近乎垂直向上。在界面附近主要是單質推進劑火焰,溫度低于遠處流場中的最終擴散火焰。

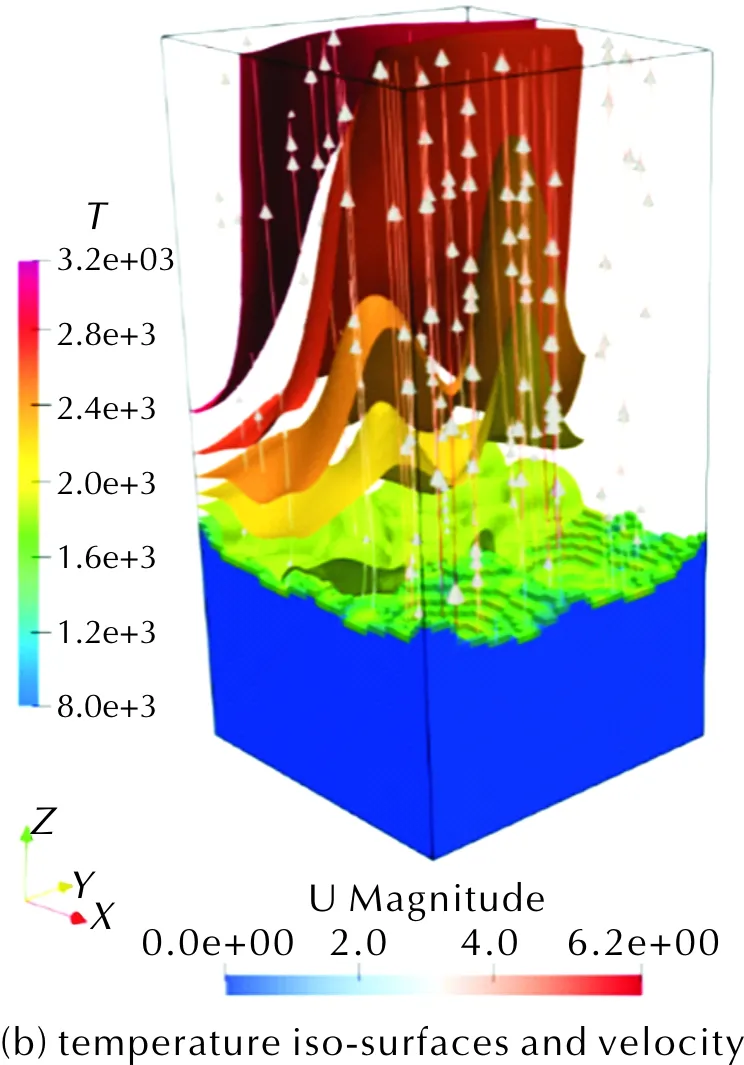
圖5 6.89MPa下M24構型在0.01s時的三維示意圖Fig.5 3D schematic diagram M24 configuration at 6.89MPa and 0.01s

圖6和圖7單獨顯示M24構型界面及固相區域的計算結構。其中圖6為同一時刻下不同壓強的情況,圖7為高壓下(13.8MPa)不同時刻的結果。觀察發現,溫度在AP與黏合劑交界附近更高。在燃燒過程中,界面會發生扭曲變形。并且熱擴散層非常薄,較高的界面溫度只能擴散到固相內很有限的距離中。在低壓情況下(2.07MPa),界面溫度較低,整體反應相對較為緩慢,界面扭曲不明顯。中壓情況(4.83和6.89MPa)界面扭曲較高壓(13.8和20.7MPa)更為劇烈,這表明較高的壓強會削弱界面上退移速度的差異,產生一個相對更平整的界面。與此同時,可以發現界面溫度隨壓強增長而提高的趨勢。

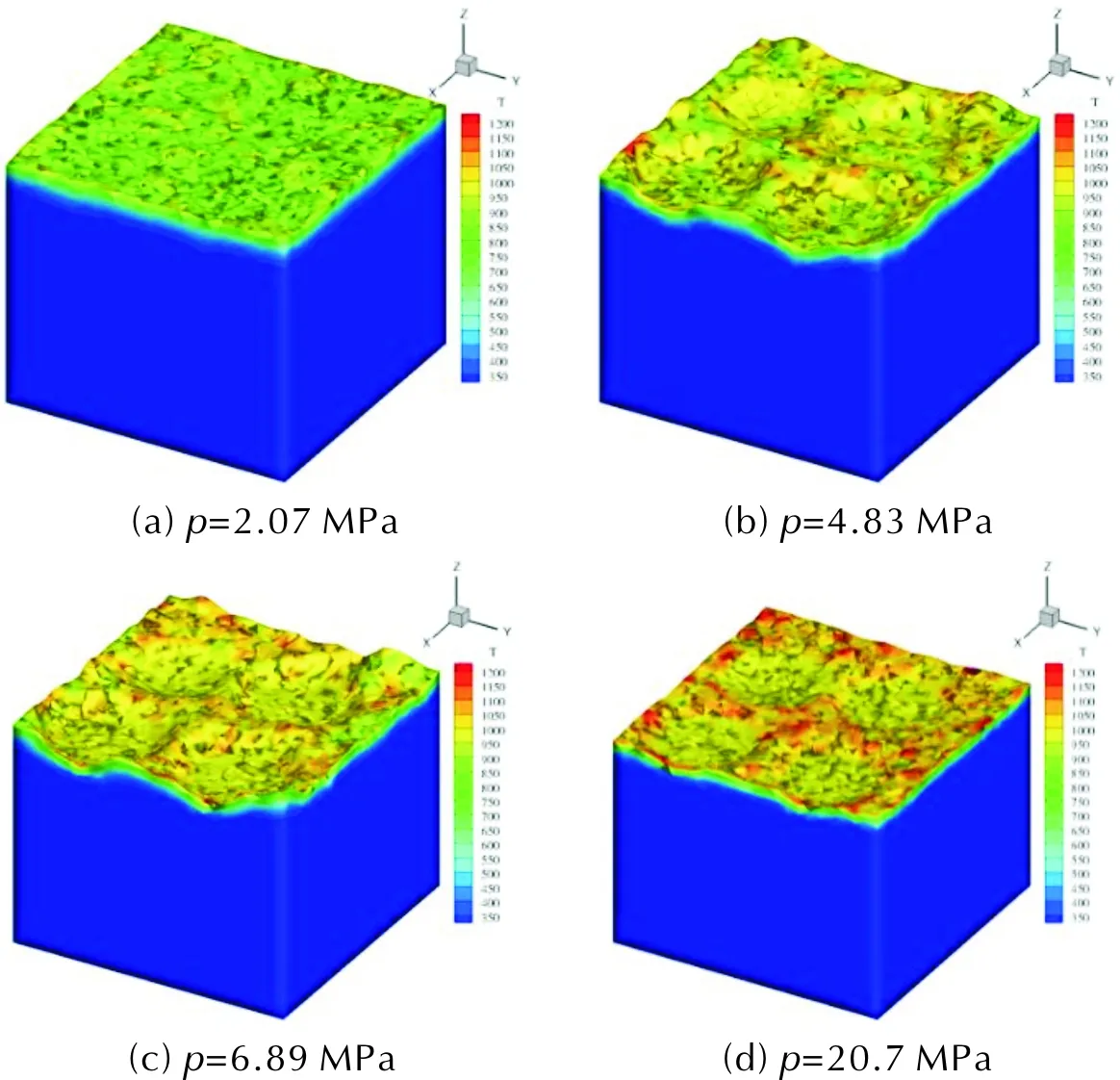
圖6 不同壓強下M24構型在0.004s時的燃燒界面Fig.6 Burning interface of M24 configuration under different pressures at 0.004s

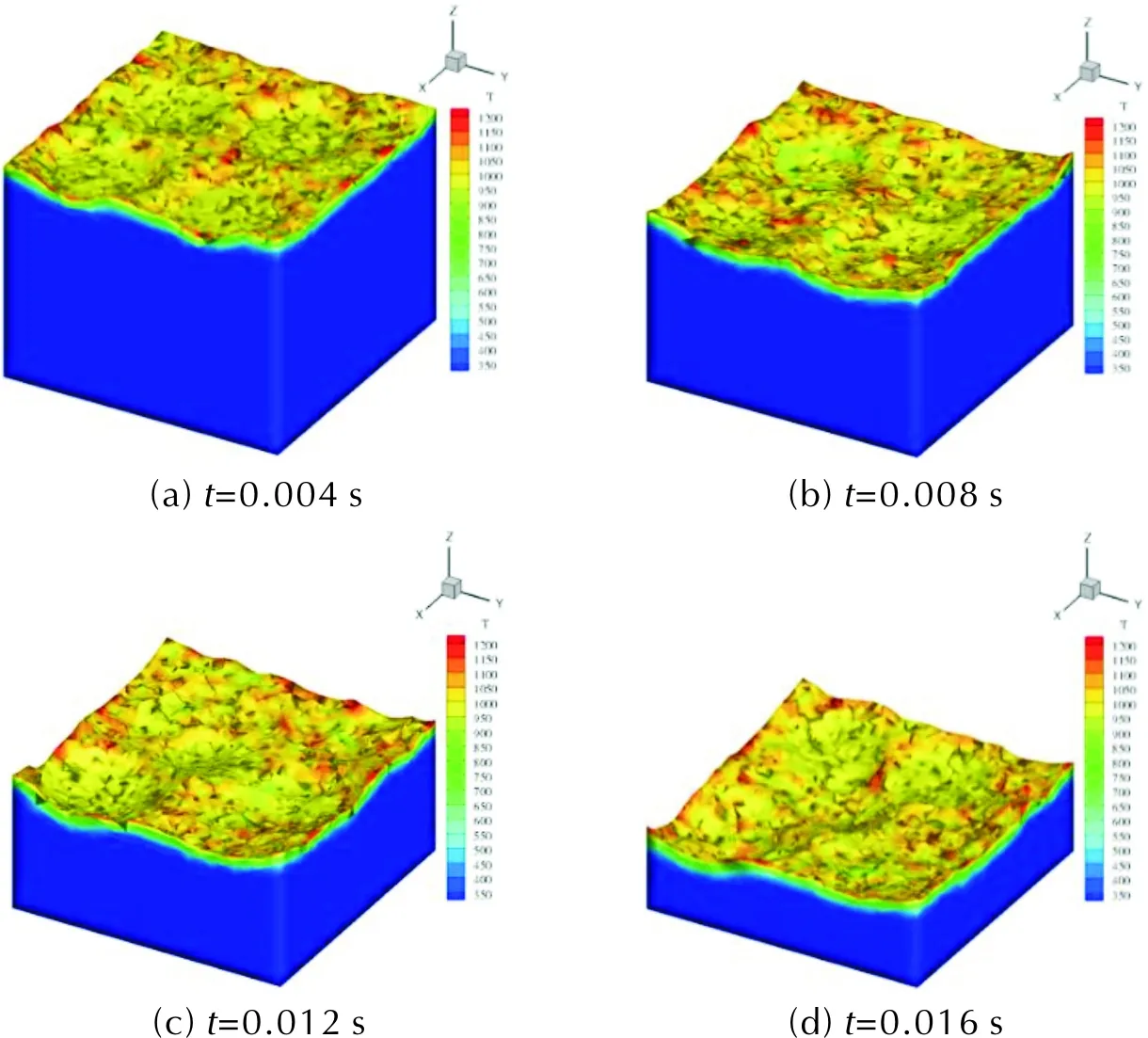
圖7 13.8MPa下不同時刻M24構型的燃燒界面Fig.7 Burning interface of M24 configuration at 13.8MPa under different instants

圖8為M24構型和M21構型壓強從0.69MPa至20.7MPa下的計算平均退移速率與實驗值及Bojko等采用Rocfire軟件包計算結果的對比[21,4]。

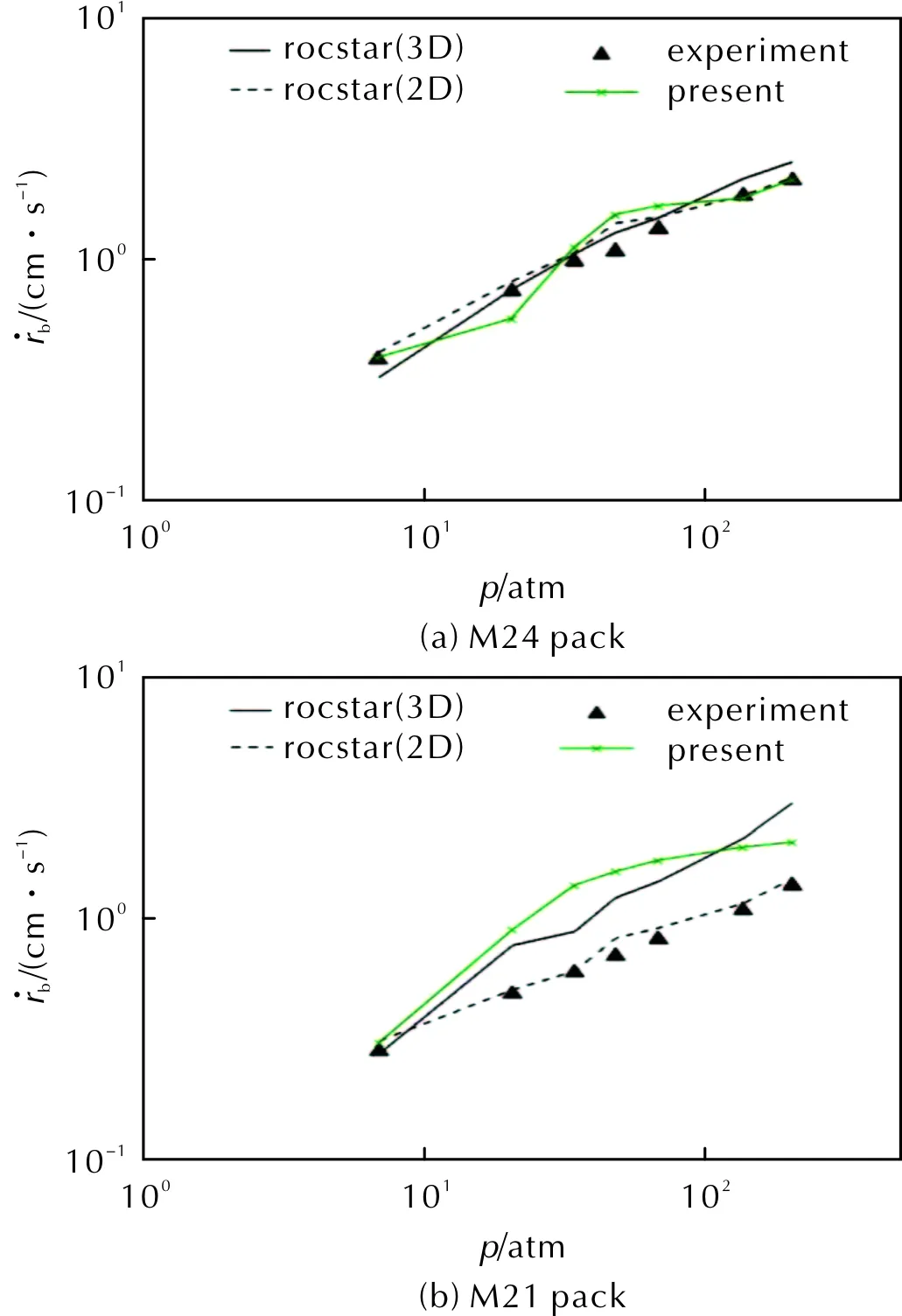
圖8 M24構型和M21構型不同壓強下界面平均退移速率的計算結果與對比Fig.8 Calculation and comparison of the mean regression rate of M24 configuration and M21 configuration, respectively under differen pressures

計算結果給出了合理的燃速大小并與實驗趨勢吻合較好。一些可能導致差異的原因包括:數值誤差和模型誤差,具體來說比如近界面網格分辨率可能不足以解析界面附近很小的溫度流場結構,以及化學動力學的選擇和固體結構刻畫中的誤差。

圖9展示了M24構型在0.007s時分別在3.45MPa和20.7MPa的情況下,由式(15)定義的氣相R1、R2及R3的化學反應速率在y方向中點切面上的云圖。如之前介紹,反應R1、R2及R3分別代表了單質推進劑火焰,基本擴散火焰和最終擴散火焰。可以發現,在兩種壓強工況下單質推進劑火焰和初級擴散火焰都非常接近界面。在高壓下,單質推進劑火焰和初級擴散火焰的化學反應速率峰值更高,說明兩種火焰在高壓情況都變得更為劇烈。對于最終擴散火焰可以發現其反應速率在高壓下更高并且火焰整體更加接近于燃面。

圖9 M24構型在3.45MPa和20.7MPa的化學反應速率Fig.9 Chemical reaction rates of M24 configuration at 3.45MPa and 20.7MPa

需要說明的是對于當前這個典型的多尺度問題,由于火焰離界面的距離非常近(大約幾微米),在高壓下,該距離將會更小,因此計算的分辨率很難滿足要求,單質推進劑火焰及初級擴散火焰這些尺度更小的結構可能沒有很好地被解析。本研究重點強調該套新提出的計算框架的合理性及初步定性定量的驗證,更高分辨率的計算和對結果的深入分析將會在進一步的研究中進行。

4 結 論

(1)本研究計算中氣相計算采用均一大小的笛卡爾網格保證計算的穩定性,固相使用非結構化網格以方便刻畫非均質粒子結構。兩套固定網格無需隨時間步重建,因此數值效率和準確性較高。

(2)非均勻退移的氣固界面由水平集方法和浸沒邊界法追蹤,質量、動量和能量的守恒關系通過對氣相內的浸沒邊界網格施加源項以保證。

(3)針對兩種構型在不同壓強條件下的燃燒過程進行的討論,該套計算框架得到的燃速與實驗及已有計算結果接近,證明該數值框架的可行性與較廣的適用性。