基于“三新”背景,掌握兩種方法*
——以立體幾何為例的大單元教學

江蘇省新海高級中學 (222006) 宋秀云

根據新課程標準的要求,高中數學新教材對應的數學課程將《立體幾何》內容分成兩部分:必修第二冊第八章《立體幾何初步》和選擇性必修第一冊第一章《空間向量與立體幾何》．第一部分內容,要求學生在掌握立體幾何的基本概念和基本知識的基礎上,重點培養學生邏輯推理能力、幾何直觀能力和空間想象能力等;第二部分內容則引入空間向量的概念,提供了解決幾何問題的新思路和新方法,拓展了學生數學視野,也有助于學生更深入的理解幾何知識．

1．實例分析

基于“三新”(新教材、新課程、新高考)背景,結合幾何學的數學史發展過程,以及立體幾何的教學要求,在解決立體幾何問題時主要借助兩種常規方法來解決問題:綜合法和向量法．下面結合最新模擬卷中的數學試題加以分析與應用,進一步對比綜合法和向量法這兩種方法在解決空間立體幾何問題中的聯系與差異．

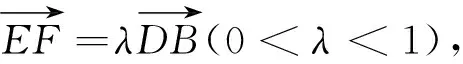
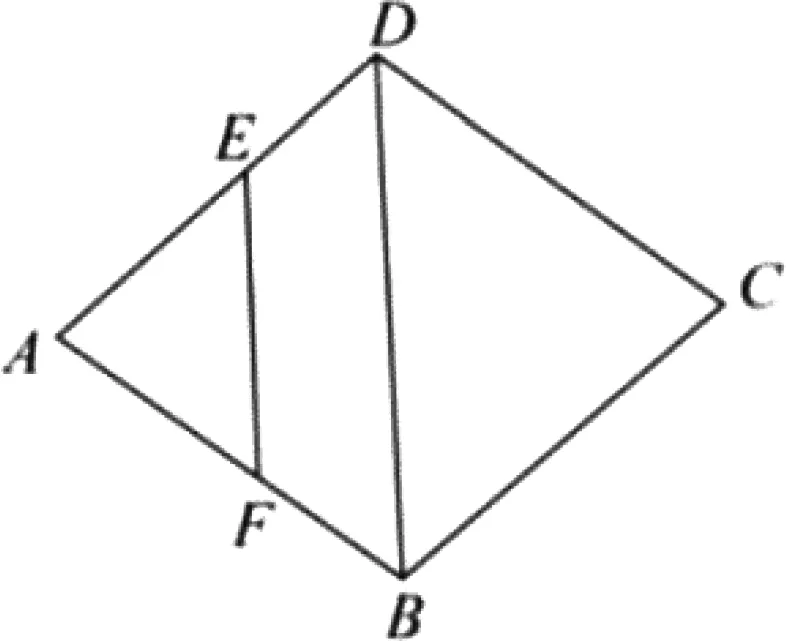
圖1

圖2

(1)當λ為何值時,BF⊥PD;

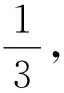
此題以圖形折疊問題來創設問題情境,第(1)小題以參數λ的求值來設置,探究線線垂直關系問題．這里既含有參數的數學運算,也含有空間元素位置關系的邏輯推理,兩者合理交匯與融合,借助平面圖形的折疊,形成疊加效應,從平面幾何到立體幾何,又從立體幾何到平面幾何,合理升降維度,巧妙數學思維;

第(2)小題以線面角的確定來設置,求解面面角的大小問題．這里以空間角中兩個最典型的線面角與面面角為條件與結論,合理創設條件來求解對應的結論,形成不同空間元素之間的關聯,構建一個更加完善的知識網絡體系．

在實際處理以上兩個問題時,都可以借助綜合法來邏輯推理,也可以借助向量法來數學運算,都可以從不同視角與層面加以分析與解決,達到解決問題的目的,真正有效考查考生的知識與能力．

2．試題解析

解析：(1)方法一：(綜合法)

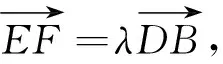
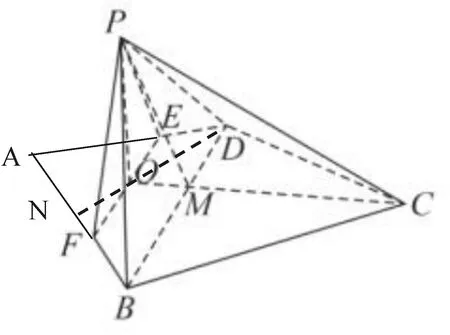
圖3

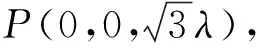
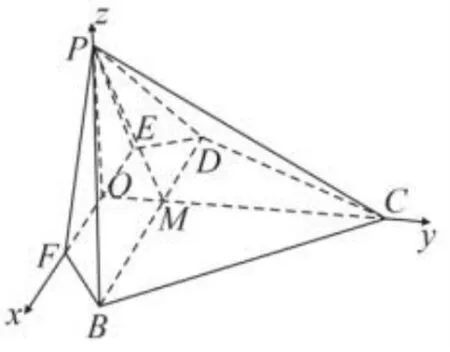
圖4

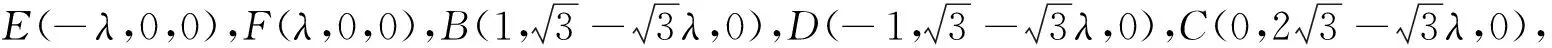
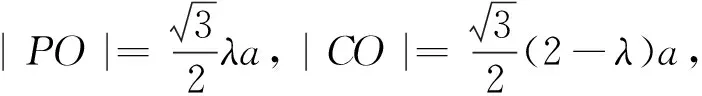
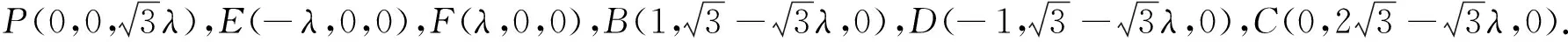
4．方法總結

在立體幾何中,判斷或處理空間元素的位置關系以及求解空間角或空間距離等問題時,綜合法和向量法是兩種最常用的分析方法．對比以上兩種解決方法以及對應的解題思路,各有千秋,各有特點．

4．1 綜合法

綜合法解決問題的依據是相關概念和定理,正確的認識概念和定理的本質是解決問題的基礎．在具體幾何圖形中,位置關系和度量關系的變化,都需要學生經歷不同層次的探索與認識,經歷觀察、想象、操作、推理等過程,對學生理解圖形本質的特征是有實質性幫助．在使用數學語言表達方面,要精準,簡明,有層次,有條理的表達出來;熟練的掌握自然語言、圖象語言和符號語言的轉化,培養學生嚴謹的邏輯推理能力．這也是重視幾何教學的一個重要原因．

同時,綜合法證明幾何元素間的位置關系主要是通過判定定理和性質定理來處理;計算角度和距離是依據作、證、求的三個過程,即,作出所要求的距離和角的輔助線,接著說明所得到的確實是按照定義或概念的距離和角,最后使用正弦定理、余弦定理等平面幾何知識來計算得到所要求問題的解．解決這類問題的技巧性較大,綜合性較強．不僅要求學生要有合情合理的邏輯推理能力,而且還需要一定的空間想象能力．

4．2 向量法

向量法在立體幾何中的運用是通過給出直線的方向向量和平面的法向量來表示空間中對應直線和平面的位置關系,一般的解題思路是按照下面三個步驟來完成:第1步建立圖形和向量的聯系,用空間向量表示問題所涉及的點、直線和平面,進而把幾何問題轉化為向量問題;第2步向量運算,通過向量的運算性質來研究幾何問題所涉及到的位置關系和計算問題;第3步翻譯,把向量運算的結果轉譯為相應的幾何意義．

運用向量法解決這類問題是把空間幾何元素之間的各種關系“隱藏”到向量的運算當中去了．這種解題方式關鍵是要求學生掌握向量這一概念體系,包括平面和空間向量概念定義,運算性質,基本定理,向量的平行、垂直、數量積的坐標運算等,以“數”研“形”,讓學生體會到空間向量解決立體幾何問題的工具性作用,進一步體會數形結合的思想方法．

在“三新”(新教材、新課程、新高考)背景下,進一步落實“雙減”政策與新改革理念,積極貫徹《總體方案》要求,高考立體幾何知識模塊的命題特色更加創新,更加開放,更加重視數學基礎知識、基本技能的掌握,更加重視數學思想方法和數學本質的理解與應用．以立體幾何為場景,新課程標準對中學數學學習提出更多、更高的要求,教學中我們需要結合必修與選擇性必修兩部分內容,注重單元教學設計的課時表達,通過綜合法與向量法單獨教學與對比教學,更好體現立體幾何教學的整體性、邏輯的連貫性、思維的系統性、思想的一致性、方法的普適性,不斷全方位、多層次地發展和培養學生數學核心素養,為所有學生的可持續發展與終身學習打下堅實的基礎．