加權空-頻時間反轉多目標成像

呼 斌 李 飛 王 偉 杜自成

(西安電子工程研究所 西安 710100)

0 引言

時間反轉(TR)是一種可以對目標進行檢測和定位的自適應傳輸技術,其廣泛應用于聲學[1]、超聲波[2]和電磁領域[3-4]。TR技術將目標的回波信號進行時間反轉操作后重新回傳到原物理介質中,可以通過物理或者合成模式使得信號自動聚焦源的位置[5]。合成模式(計算TR)通過傳播介質的格林函數來數值合成反向傳播場的數據[6]。

兩種主要的TR成像方法分別是TR算子分解算法[7](DORT)和TR多信號分類算法[8](TR-MUSIC)。DORT算法通過TR算子的信號子空間對應的特征向量構造成像函數,TR-MUSIC類的方法則是依靠噪聲子空間對應的特征向量。這類算法都是基于對多站數據矩陣(MDM)的奇異值分解(SVD)。成像結果受MDM的秩(與散射點個數相關)的影響較大,尤其是當天線陣元數量較少時,成像結果對選取的噪聲子空間向量的數量更為敏感。因此,對數據SVD后并根據矩陣的秩來適當地劃分信號子空間和噪聲子空間顯得尤為重要。這兩種方法都需要知道散射體的數量,這通常是通過文獻[13-14]中的方法獲得的。或者,TR成像函數可以通過統計測試[15]的方式來設計,因此可以不需要精確的目標數。類似的方法[16-17]在雷達相關應用中有著廣泛應用。

本文中,提出了一種簡單的近場成像方法,它對基于傳統的計算TR成像方法中需要的目標確切數量不敏感。同時,研究了在成像中數據矩陣秩的確定(通過對MDM進行SVD獲得)對成像結果的影響。本文提出的方法采用MDM的奇異值來加權TR成像函數,并確定了初始目標的數量。然后,提出了一種被改進的SF-TR,即W-SF-TR算法,獲得穩定的 TR成像結果,并從理論分析了提高成像性能的原因。最后,給出了一些簡單散射場景的數值算例驗證了導出的結果。所有的結果都是基于自由空間背景假設,忽略了天線間的相互耦合、極化等影響。

本文的其余部分安排為:第二部分簡要介紹了SF-MDM和SF-TR成像方法。提出了一種新的W-SF-TR成像算法。然后,第三部分給出了W-SF-TR算法的理論性能分析,并通過數值模擬對其進行了驗證。最后,第四部分總結得出了結論。

符號表示:大寫或小寫的黑體字母表示向量或者矩陣;(·)H、(·)T, |·|以及Σ表示矩陣共軛轉置、轉置、絕對值和求和。

1 W-SF-TR成像算法

1.1 SF-TR算法

假設TR陣列包含N個天線陣元,TR陣列的第一個陣元發射所需的寬帶信號,陣列記錄下目標的回波數據,具體模型如圖1所示。

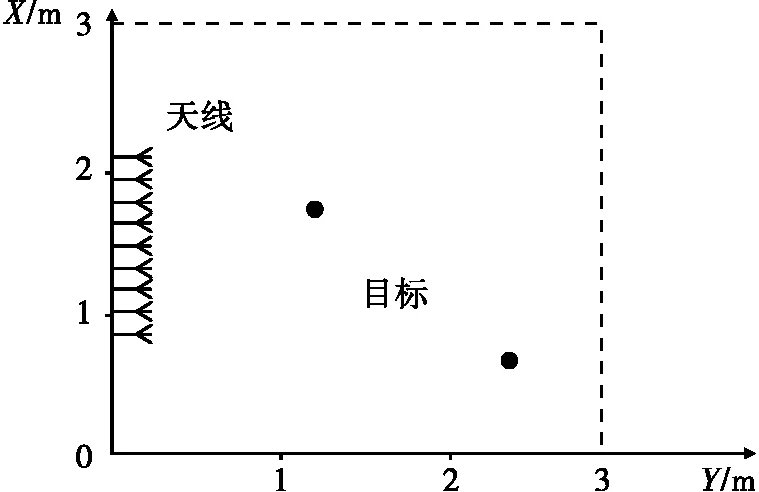
圖1 多目標成像場景示意圖

然后,將回波信號經過傅里葉變換轉換到頻域表示。設置采樣頻點個數為L。因此,空頻多站數據矩陣(SF-MDM)可以表示為式(1)所示。

(1)

其中:ki(ωj), (i=1, 2, … ,N;j=1, 2, … ,L),表示第i個陣元接收到的回波信號在頻域對應的第j個頻點的均勻采樣;ωL-ω1表示信號的帶寬。

對K進行奇異值分解可得

K=UΛVH

(2)

其中:U是一個N×N的酉矩陣,其中的列向量為左奇異向量;V是一個L×L的酉矩陣,其中的列向量表示右奇異向量;Λ是一個N×L矩陣,其對角線元素表示相應的奇異值,這里U可以表示為

(3)

其中:ui表示第i個N×1的左奇異向量包含著空間(位置)信息[11]。其中,P-1個較大的奇異值對應的左奇異向量ui(i=1, 2, …,P-1)表示有P-1個較強的散射點,并構成了信號子空間;其余的左奇異向量ui(i=P, 2, …,N)對應U矩陣中較小的奇異值,并構成了噪聲子空間。這里采用文獻[12]中的方法,通過選擇連續奇異值比值中的最大值確定P值,即通過公式(4)確定P值為

(4)

其中λn表示第n個奇異值。

SF-TR算法利用噪聲子空間對目標進行成像,其成像公式可以表示為

(5)

其中,g(rs,ω)表示在探測區域的每個搜索位置rs處的背景格林函數向量,表示為

g(rs,ω)=[G(rs,r1,ω),G(rs,r2,ω),…,G(rs,rN,ω)]T

(6)

其中的每個元素G(rs,rN,ω)表示一個背景格林函數;rN表示第N個天線陣元的位置;ω表示角頻率。

1.2 加權SF-TR算法(W-SF-TR)

在多目標成像場景中,P值的選取可能會影響成像的質量。因為P的大小決定了信號子空間或噪聲子空間的大小,特別是當陣列中陣元數量較小時,P的不同值可能會嚴重影響了成像結果。因此,在所提出的W-SF-TR算法中,奇異值用于加權對應的左奇異向量,然后重新構造噪聲子空間以減少噪聲子空間大小對圖像質量的影響。參考SF-TR成像公式(5),提出的W-SF-TR成像算法可以描述為

(7)

其中,λi(i=P,P+1, …,N)表示對應的奇異值。

2 W-SF-TR成像結果與討論

通過矩量法(MOM)獲得了自由空間中目標的SF-MDM。圖1所示的即為多目標近場TR成像場景,構成一個3m×3m的探測區域。均勻間隔的線陣由9個偶極子天線構成,沿著x軸分布,間距為λc/2,其中λc為自由空間中心頻率對應的波長。發射信號的中心頻率fc=3GHz,帶寬為400MHz,變換到頻域的頻率采樣點數L=101。陣列的幾何中心位于(0.1m,1.5m,0m)處。兩個半徑為5cm的理想導體金屬球分別位于(1.8m,1.2m,0m)和(0.8m,2.4m,0m)處。

2.1 W-SF-TR算法成像穩健性分析

在本小節中,我們分析了W-SF-TR算法在成像性能中的優越性。

首先,我們計算得出了在不同的SNR條件下的奇異值分布,如圖2所示。在理想情況下(無噪聲的情況),奇異值的分布曲線顯示前兩個奇異值較大,第三、第四、第五個奇異值大于0,其余奇異值較小。然而,隨著SNR的降低,與噪聲子空間相對應的奇異值逐漸增大,因此很難直接通過奇異值的相對大小區分信號子空間和噪聲子空間。

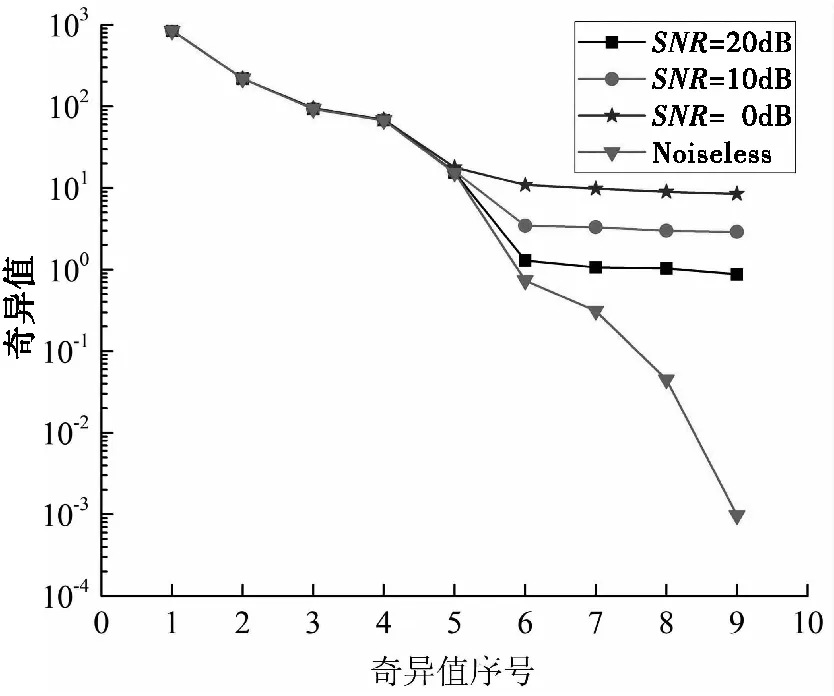
圖2 不同信噪比條件下的奇異值分布對比

圖3展示了不同SNR條件下連續奇異值的比值。根據式(4)和圖3給出的結果可以看出,當SNR逐漸降低時,P在不同SNR條件下的對應值分別為9、6、6和2,對P值有顯著影響。

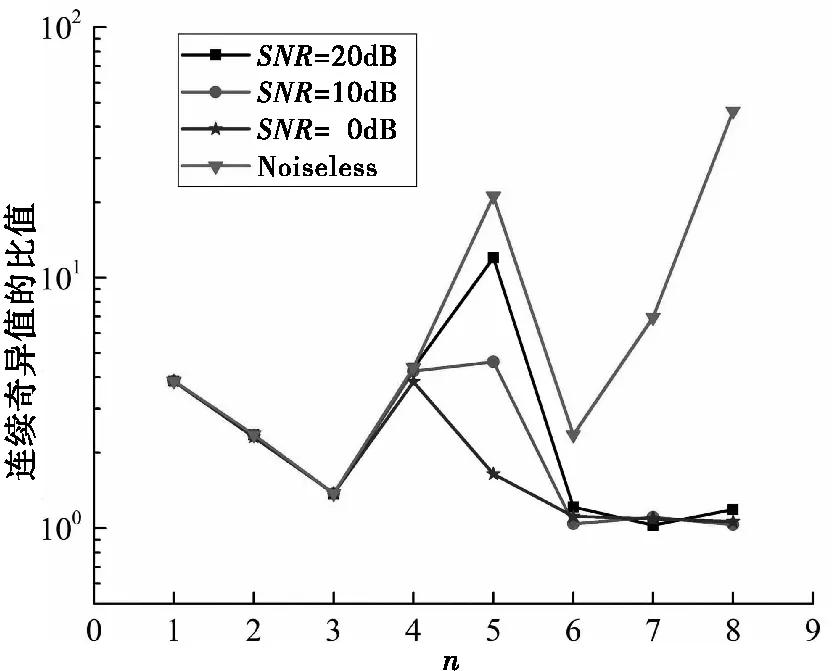
圖3 不同信噪比條件下的連續奇異值比值

為了更直觀地說明這個問題,當P的取值從3～8變化時,分別獲得2個目標點的SF-TR成像結果。圖4為SNR=0dB時P取不同值時的SF-TR成像結果(在圖4和圖5中,符號×代表了兩個目標的實際位置)。當P=3和P=4時,目標位置的能量不能較好的聚焦,目標的位置難以確定。能量散布在如圖4(a)所示的較大范圍面積上。隨著P的增加,對目標的聚焦效果逐漸變得更好。從圖4的結果可以得出結論:噪聲子空間的選擇對多個目標的SF-TR成像結果影響非常大。P的值決定了如何區分信號子空間和噪聲子空間,極大地影響了成像結果,并隨著SNR的變化而變得不穩定。

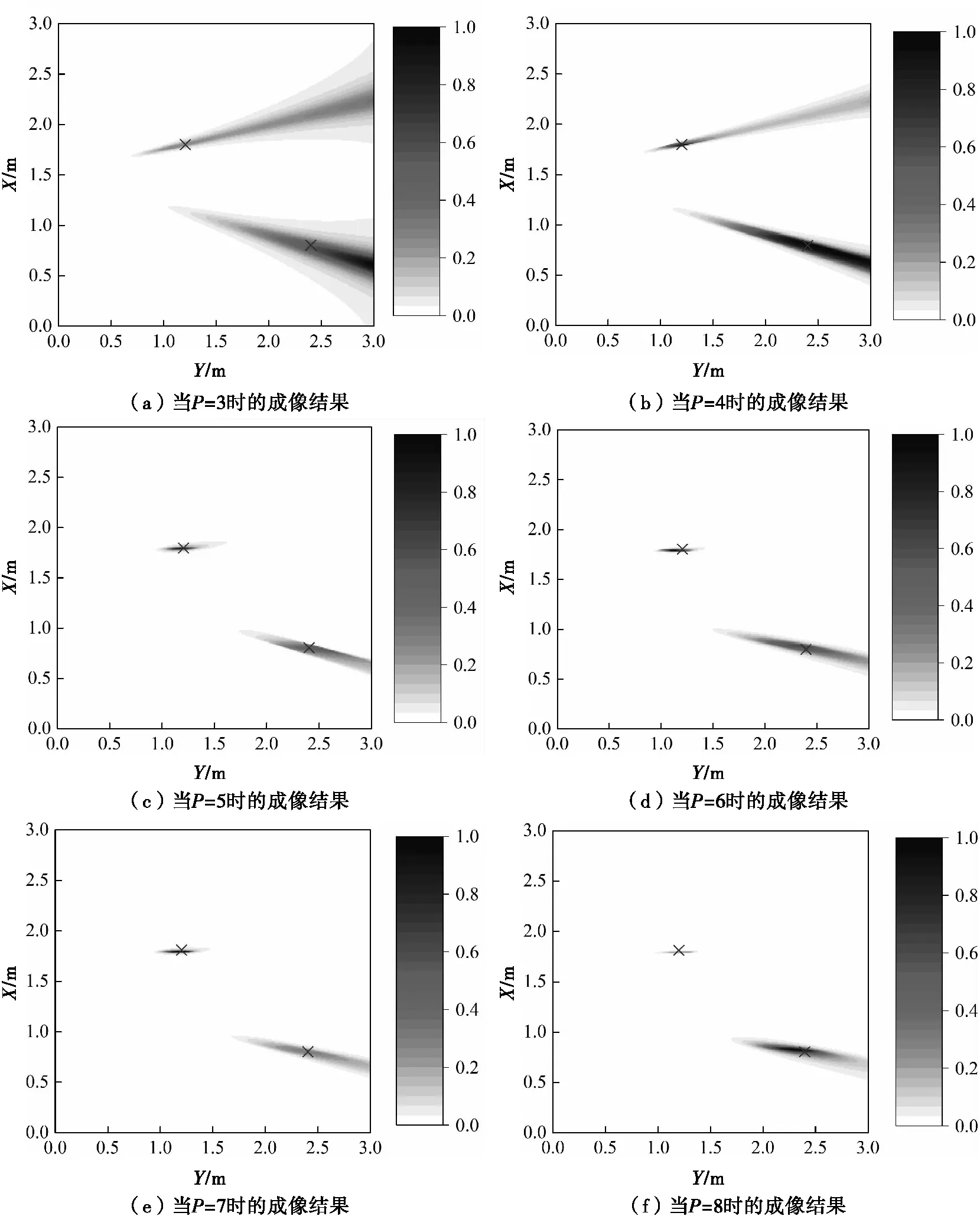
圖4 多目標SF-TR成像結果(SNR=0dB)

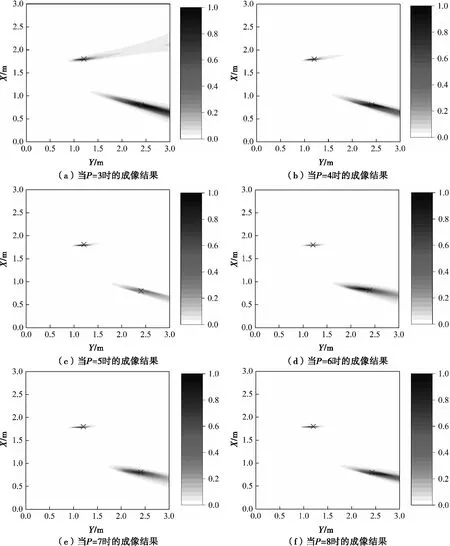
圖5 多目標W-SF-TR成像結果(SNR=0dB)

其次,分析了W-SF-TR的成像穩定性和分辨率。假設我們已經劃分的噪聲子空間有N-P+1個向量構成,對應的奇異值符合式(8)形式。

λP≥λP+1≥…≥λQ≥λQ+1≥…≥λN≥0

(8)

假設噪聲子空間中包含的Q-P-1個向量(Q≥P-1)本應屬于信號子空間,卻被誤劃分到噪聲子空間。因此,式(7)的分母可以分為兩部分,進一步表示為

(9)

這里應該注意到當Q=P-1時,式(9)右側的第一項為0。

類似的,我們可以將式(5)重新表示為

(10)

根據式(8)、式(9)和式(10)可得

(11)

經過進一步運算,可得

(12)

式(12)中,第一項表示使用W-SF-TR算法后,噪聲子空間部分與信號子空間部分(被錯誤分類到噪聲子空間的部分)的比值;最后一項表示,在SF-TR中噪聲子空間部分與信號子空間部分(被錯誤分類到噪聲子空間的部分)的比值。這表明,奇異值向量的加權使在分母上的真實噪聲子空間向量的比例增加,而一些被錯誤分類為噪聲子空間的信號子空間向量的比例減小。因此,這些信號子空間向量被意外分配噪聲子空間中造成的影響降低。

2.2 多目標W-SF-TR成像

在W-SF-TR成像過程中,式(7)被用于對兩個目標進行成像。在圖5(a)、圖5(b)和圖5(f)中,可以清楚地看到在使用W-SF-TR算法后,目標的成像結果優于圖4中的相應未使用該算法時的結果。W-SF-TR算法對兩個目標的成像位置與相應目標的實際位置相匹配。因此,隨著P的變化,我們提出的成像方法將更多的能量集中在兩個目標上,并且在低SNR情況下成像結果更加穩定。同時,在使用W-SF-TR后,P值的可選范圍變得比SF-TR算法更大,成像結果對噪聲子空間的選擇變得不那么敏感。

2.3 W-SF-TR算法目標分辨率

為了進一步比較SF-TR算法和W-SF-TR算法的性能,圖6和圖7分別給出了兩種算法的歸一化橫向和縱向分辨率對比。SF-TR算法的橫向和縱向分辨率隨著P值的變化產生明顯變化。通過將W-SF-TR算法應用到SF-MDM中,當噪聲子空間如圖6所示時,我們實現了對多目標穩定的橫向和縱向分辨。從圖6(a)可以看出,當選擇了不同的P值時,能量集中在SF-TR算法的兩個目標上發生了顯著的變化。當P的值為3和4時,橫向分辨率非常差,能量很難集中在兩個目標上。當P的值在3～8范圍內變化時,在X=0.8m和X=1.8m的兩個目標位置處的聚焦能量差分別達到28.9dB和24.5dB。

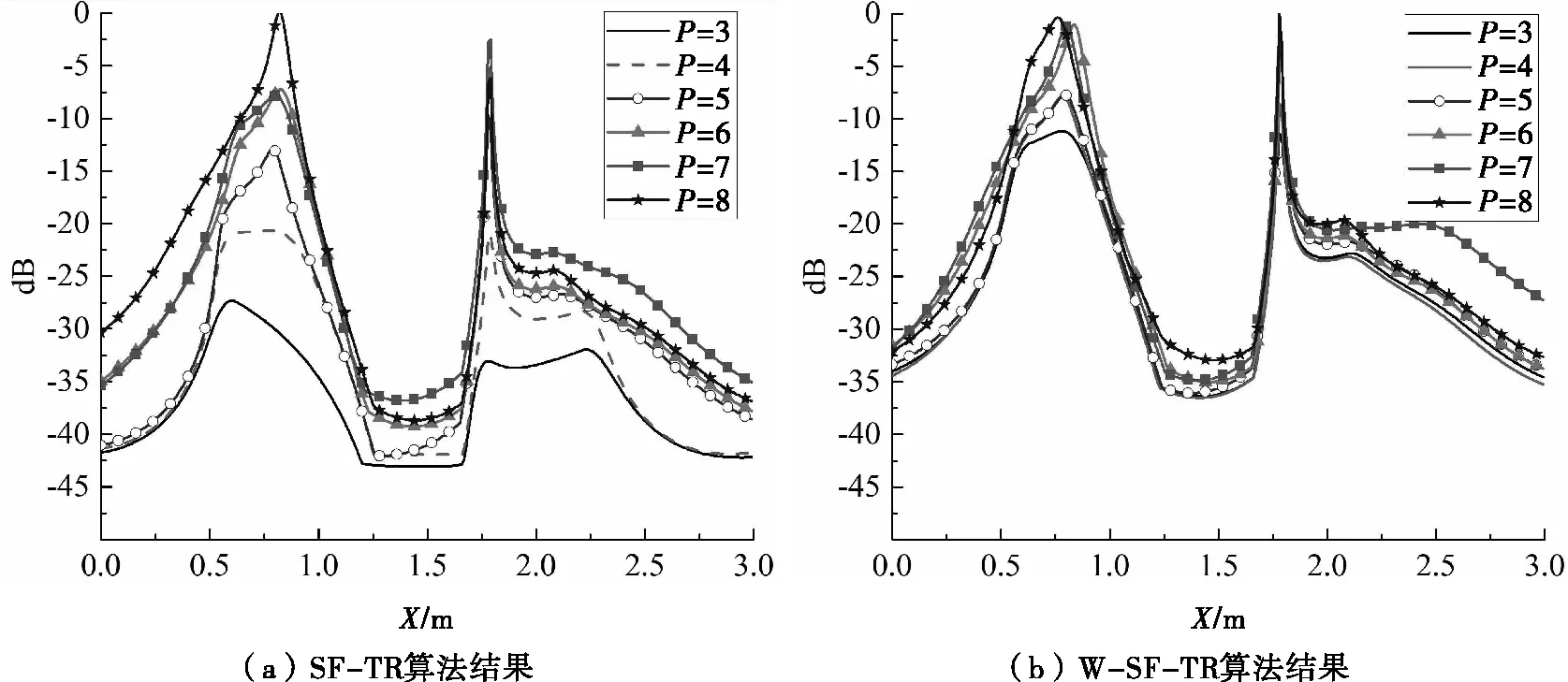
圖6 兩目標TR成像的橫向分辨結果對比(SNR=0dB)

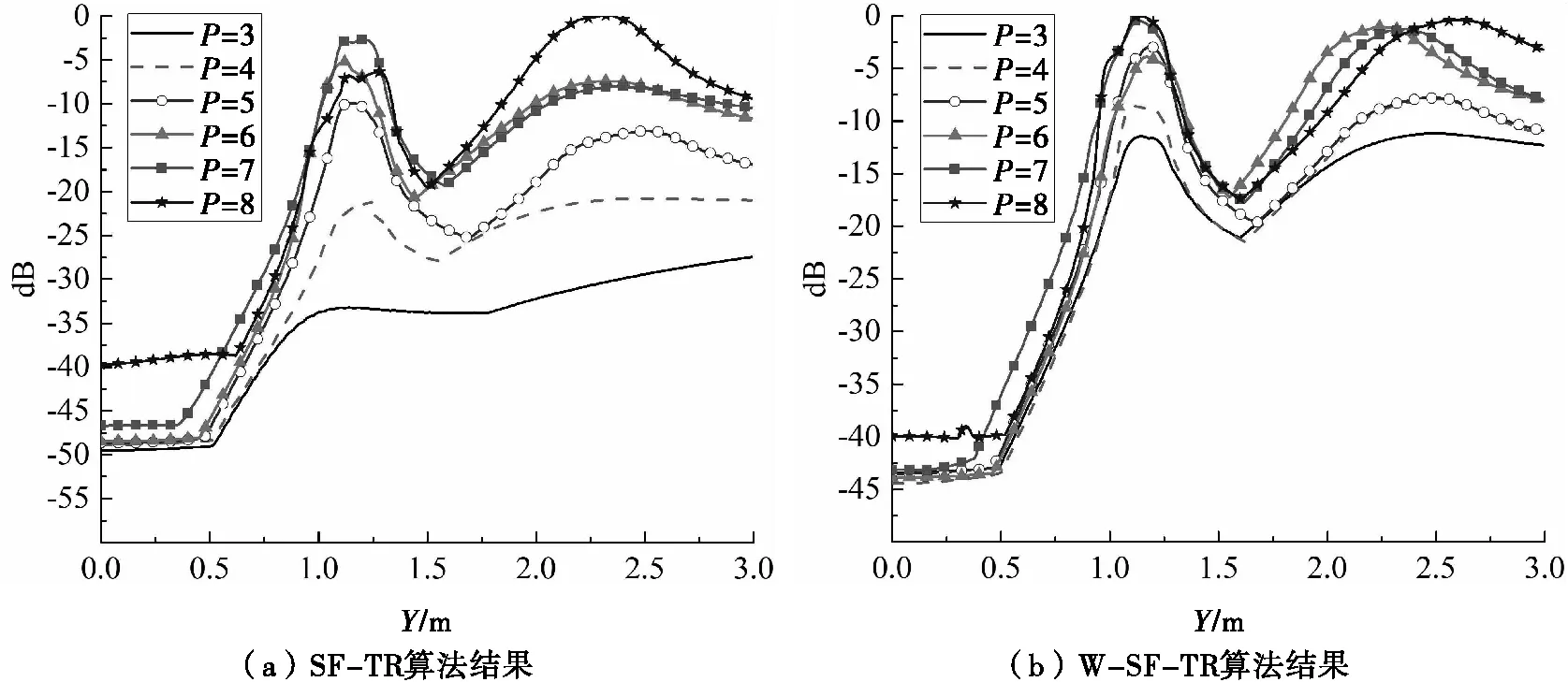
圖7 兩目標TR成像的距離向分辨結果對比(SNR=0dB)

圖6和圖7的對比結果表明,SF-TR成像算法對P值的選取非常敏感,即噪聲子空間的大小。在使用本文提出的W-SF-TR算法后,如圖6(b)所示,在X=0.8m和X=1.8 m處的兩個目標的聚焦能量差值分別顯著降低到10.0dB和5.3dB。類似地,圖7中的對比結果也表明,W-SF-TR算法的距離分辨效果也優于SF-TR算法。當P的值變化時,在Y=1.2 m和Y=2.4m處的兩個目標的聚焦能量波動范圍分別達到了30.6dB和29.5dB。通過采用W-SF-TR算法,其波動范圍減少到11.0dB和10.1dB。

總的來說,給出的成像結果表明W-SF-TR算法可以在橫向和距離向實現目標的高分辨成像,并在低信噪比、P值變化的情況下獲得穩定的成像結果。因此可以從W-SF-TR成像結果中得出結論:該方法可以自適應的調整TR成像的負面影響,并在P變化時進行穩定成像。

3 結束語

本文提出了多目標近場W-SF-TR成像算法,該算法克服了傳統SF-TR成像算法在選擇不同P值時造成的潛在不穩定成像結果。新算法通過引入噪聲子空間向量加權因子(對應的奇異值),使得確定噪聲子空間大小的P值的選擇范圍擴展到一個較大的動態范圍。當P在大范圍內波動選取時,W-SF-TR算法仍然可以取得優異的成像結果,這也有利于移動目標成像。在低SNR的情況下,通過兩個近場PEC目標驗證了W-SF-TR算法的有效性。結果顯示,在對多目標進行TR成像時,提出的W-SF-TR算法表現優異,顯示出了穩定的成像效果。此外,W-SF-TR算法對多目標的成像分辨穩健能力也優于SF-TR算法。