帶骨式削弱彎曲型耗能梁K形偏心支撐框架抗震性能研究

于海豐 王煒 吳楊周 馬康 王焱

摘 要：為提高彎曲型耗能梁塑性變形能力，提出一種帶骨式削弱的彎曲型耗能梁K形偏心支撐結構。采用數值模擬方法研究削弱起點a、削弱深度c及耗能梁加勁肋間距等關鍵設計參數對帶骨式削弱的彎曲型耗能梁K形偏心支撐結構抗震性能的影響，對比削弱模型與Base模型之間的承載能力、剛度及耗能能力等性能指標。結果表明，當削弱起點a取值在2h_f～3h_f之間、削弱深度c取值在2t_f～4t_f之間及加勁肋間距為0.7b_f左右時，削弱模型與Base模型各性能指標相差不大。帶骨式削弱設計及加勁肋間距能夠使耗能梁端部翼緣更大區域出現彎曲塑性變形，提升耗能能力，為后續進行彎曲型偏心支撐結構抗震性能研究提供參考。

關鍵詞：結構設計；偏心支撐鋼框架；彎曲型耗能梁；骨式削弱；抗震性能

中圖分類號：TU391

文獻標識碼：A DOI：10.7535/hbkd.2023yx03009

收稿日期：2022-11-22；修回日期：2023-03-01；責任編輯：馮 民

基金項目：河北省自然科學基金（E2021208010，E2019208322）

第一作者簡介：

于海豐（1980—），男，遼寧興城人，教授，博士，主要從事鋼結構方面的研究。

通信作者：王 煒。E-mail： wangwei@hebmail.gov.cn

Study on seismic behaviour of K-eccentrically braced steel frame with dog-bone reduced flexural link

YU Haifeng^1，2，3，? WANG Wei⁴，? WU Yangzhou¹，? MA Kang^1，2，3，? WANG Yan¹

（1.School of Civil Engineering， Hebei University of Science and Technology， Shijiazhuang， Hebei 050018， China; 2. Innovation Center of Disaster Prevention and Mitigation Technology for Geotechnical and Structural Systems of Hebei Province （Preparation）， Shijiazhuang， Hebei 050018， China; 3. Engineering Technology Research Center for Intelligent & Low-carbon Assembled Building， Shijiazhuang， Hebei 050018， China; 4. Housing Market Research and Development Center of Hebei Province， Shijiazhuang， Hebei 050051， China）

Abstract：In order to improve the plastic deformation capacity of flexural links， a K-eccentrically braced steel frame structure with the dog-bone reduced flexural link was proposed. The effects of the key parameters， such as the weakening starting point a and the weakening depth c， as well as the link spacing of the stiffeners on the seismic performance of the K-eccentrically braced steel frame structure were investigated by numerical simulations. The load carrying capacity， stiffness and energy dissipation capacity between the weakened model and the Base model were compared. The result shows that the weakening starting point a is in the range of 2h_fto 3h_f， the weakening depth c is in the range of 2t_fto 4t_f， and the spacing between stiffener is about 0.7b_f， indicating that the difference between the performance of the weakened model and the Base model is not significant. The proposed dog-bone reduced design and the link spacing of the stiffeners can lead to bending plastic deformation in a larger area of the link， so that the energy-dissipating capacity of link is improved， which has some reference value for further study of flexural eccentrically braced steel frame in seismic performance.

Keywords：structure design; eccentrically braced steel structure; flexural links; dog-bone reduced; seismic performance

在地震作用下偏心支撐鋼框架主要通過耗能梁段發生剪切塑性變形（剪切型偏心支撐結構）^［1-5］或彎曲塑性變形（彎曲型偏心支撐結構）

^［6-10］來耗散能量，從而保護框架梁、柱、支撐等非耗能構件，是一種較好的抗震結構體系^［11-14］。根據耗能梁段的受力機理可知，當其發生剪切塑性變形時，塑性鉸會均勻分布在腹板上；而當發生彎曲塑性變形時，塑性鉸主要分布在耗能梁端部的上下翼緣局部區域，耗能能力略差

^［15-18］。因此，彎曲型偏心支撐結構在工程中的應用較少，但耗能梁長度較長有利于結構空間布局，故對彎曲型偏心支撐結構的抗震性能開展研究是十分有必要的。目前，國內外學者對骨式削弱的研究主要集中在梁柱連接區域，對于彎曲型耗能梁則未見報道。

為改善彎曲型偏心支撐結構的抗震性能，提高其材料利用率，本文提出一種帶骨式削弱的彎曲型偏心支撐結構，即對耗能梁上下翼緣受力較小的區域進行圓弧形骨式削弱，以使其受力大小與所需翼緣截面面積盡量相匹配。

為驗證帶骨式削弱的彎曲型耗能梁偏心支撐結構的性能優劣，本文擬采用ABAQUS軟件建立相應的有限元模型并對其進行單調和循環加載，研究不同的削弱面積對結構荷載位移曲線、承載力、剛度及耗能能力的影響。

在此基礎上，分析耗能梁區域加勁肋的布置對結構抗震性能的影響，給出帶骨式削弱彎曲型耗能梁偏心支撐結構的設計建議。

1 有限元方法驗證

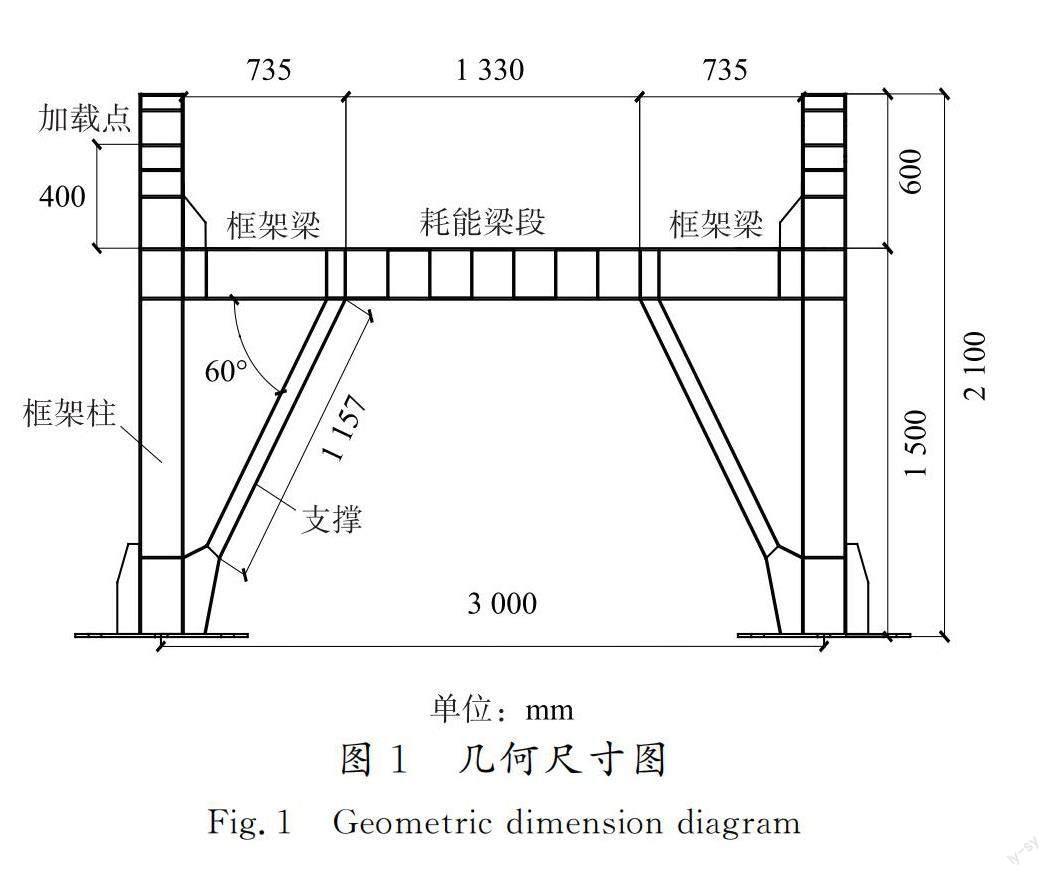
為驗證有限元方法的合理性及分析結果的正確性，本文采用ABAQUS有限元軟件對某彎曲型偏心支撐結構的擬靜力試驗進行模擬驗證。試驗模型高度1 500 mm，跨度3 000 mm，構件之間均采用全熔透焊縫連接，使用Q235B級鋼材，框架底部通過螺栓與地梁連接，試驗時在側面設置側向支撐以防止結構出現面外變形，試驗詳細信息見文獻［19］。數值模型幾何尺寸見圖1，各構件截面尺寸見表1。

加載制度與試驗一致，采用Von Mises多線性隨動強化的三折線模型，考慮Bauschinger效應，力學性能見表2。采用殼單元S4R建立有限元模型，各構件之間采用tie約束。單元網格與邊界約束條件見圖2。柱腳自由度全部約束以模擬剛接，通過令U_x=0來模擬耗能梁段的面外約束。另外，在支撐跨中施加l/500的面外變形（l為支撐長度）來模擬支撐可能的面外缺陷，通過在加載點（加載點耦合）同時施加荷載/位移來模擬試驗加載方式。

表3及圖3為部分有限元與試驗結果的對比。試驗的承載力及剛度要略大于有限元，兩者相差在7%以內；由于有限元分析時未能充分考慮材料硬化現象且試驗模型中各種阻尼作用的存在，比如滾軸與框架之間的摩擦等因素存在，使得數值模擬得出的滯回曲線與試驗相比要略微飽滿，但總體吻合程度較好；試驗及數值模擬的耗能梁段變形（端部上下翼緣局部屈曲）及結構整體變形基本一致。綜上，可采用數值方法開展偏心支撐鋼框架結構的抗震性能研究。

2 參數化分析

2.1 有限元模型建立

圖4為骨式削弱的耗能梁示意圖。圖中a為削弱起點（即開始削弱的位置）到耗能梁端部之間的距離，b為削弱長度（即2個削弱起點之間的距離），c為削弱深度（即圓弧上最高點到耗能梁翼緣外邊緣的垂直距離），e為耗能梁長度，R為削弱半徑，其中b=e-2a，R=4c²+（e-2a）²/8c。當耗能梁長度e一定時，骨式削弱只需確定a和c即可。基于試驗模型（見圖1，未削弱模型，命名為Base模型），本文分析了參數a和c的變化對結構抗震性能的影響。具體參數見表4。

基于有限元法建立數值模型，建模細節與第一節相同。循環加載時采用位移控制法，初始位移值和每個加載級的增量均為8 mm，且每個加載級別循環2周。大量試算表明，有限元分析的承載力在加載后期未出現明顯下降，故當位移加至64 mm時（層間位移角1/23）停止分析；單調加載時，加載至150 mm（層間位移角1/10）時停止分析。

2.2 削弱起點a的影響

2.2.1 荷載位移曲線與耗能分析

圖5給出了單調及循環加載下各模型的荷載位移曲線。單調加載時，加載位移不大于8 mm時各模型的荷載位移曲線基本為直線且幾乎重合。隨著進一步加載，當耗能梁段進入塑性，荷載位移曲線出現明顯轉折，M_a-2bf，M_a-3bf，M_a-4bf模型的荷載位移曲線與Base模型的基本重合，略高于M_a-bf和M_a-0模型，M_a-0模型承載力最小。循環加載時，與單調加載時結果類似，M_a-2bf，M_a-3bf，M_a-4bf模型的滯回曲線與Base模型的基本重合，M_a-0，M_a-bf模型的滯回曲線面積要小于其余模型。

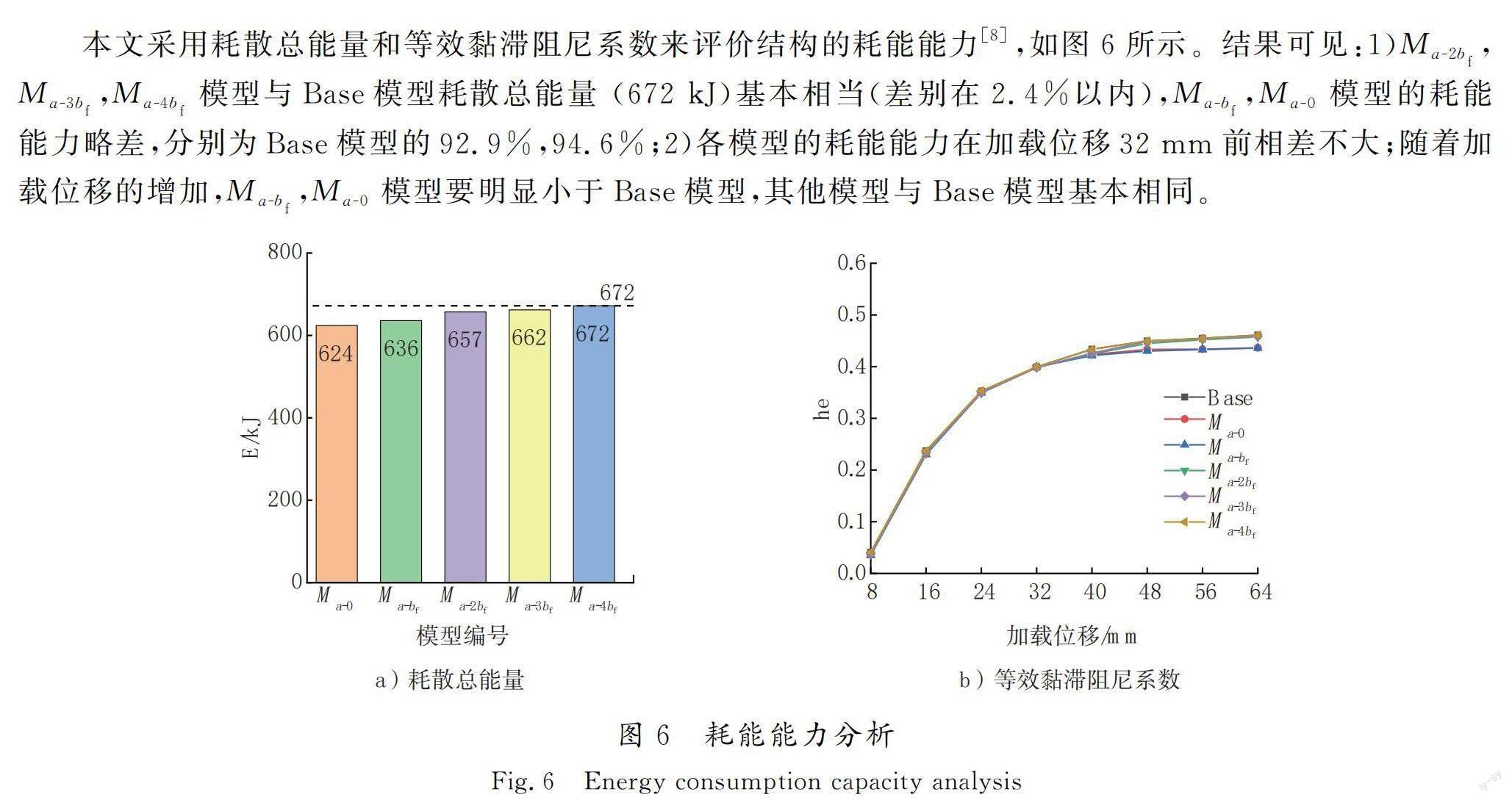
本文采用耗散總能量和等效黏滯阻尼系數來評價結構的耗能能力^［8］，如圖6所示。結果可見：1）M_a-2bf，M_a-3bf，M_a-4bf模型與Base模型耗散總能量 （672 kJ）基本相當（差別在2.4%以內），M_a-bf，M_a-0模型的耗能能力略差，分別為Base模型的92.9%，94.6%；2）各模型的耗能能力在加載位移32 mm前相差不大；隨著加載位移的增加，M_a-bf，M_a-0模型要明顯小于Base模型，其他模型與Base模型基本相同。

2.2.2 承載力與剛度分析

循環加載下，各模型的骨架曲線及剛度退化曲線見圖7，部分特征點響應見表5。由于相同加載級下推拉方向承載力基本相同，故本文只對推方向的特征點值進行分析。結果可見：1）各模型骨架曲線幾乎重合，轉折（結構屈服）位置無明顯差別。相較而言，M_a-2bf，M_a-3bf，M_a-4bf模型的屈服荷載、峰值荷載、屈服位移與Base模型的基本相等，略大于M_a-0，M_a-bf模型。2）各模型剛度退化曲線趨勢相同，加載位移小于16 mm時，耗能梁的塑性逐步發展，剛度退化速率較快；加載位移大于16 mm時，耗能梁的塑性發展趨于穩定，剛度退化趨于平緩且各曲線基本重合。相較而言，Base模型初始剛度最大，M_a-0模型的最小，其余各模型介于兩者之間。總體上，削弱起點a的變化對結構屈服荷載（相差2.1%以內）的影響要小于對峰值荷載（相差5.9%以內）及初始剛度（相差4.5%以內）的影響。

理論上，削弱起點可以從耗能梁端部開始，即a=0 mm，但分析表明M_a-0模型的承載力與耗能能力均低于Base模型。原因在于，彎曲型耗能梁屈服會在耗能梁端部上下翼緣的局部區域形成塑性鉸，當a較小時會減小翼緣有效的屈服面積（見圖8 a）），隨著a值的增加，削弱逐漸遠離屈服區域（見圖8 b）），故M_a-2bf，M_a-3bf，M_a-4bf模型的各項抗震性能指標與Base模型相差不大，因此建議a的取值范圍為2b_f～3b_f。

2.3 削弱深度c的影響

2.3.1 荷載位移曲線與耗能分析

圖9給出了單調及循環加載下各模型的荷載位移曲線。單調加載時，各模型的荷載位移曲線基本重合，表明削弱深度c對單調加載的承載力影響較小。循環加載時，M_c-2tf，M_c-3tf模型的滯回曲線與Base模型的基本重合，其余模型的滯回曲線要明顯小于Base模型。

圖10給出了循環加載下各模型的耗能能力結果。由圖10可知：1）M_c-2tf，M_c-3tf，M_c-4tf，M_c-5tf，M_c-6tf模型耗散的總能量分別為661，657，633，620和613 kJ，較Base模型分別減小1.6%，2.2%，5.8%，7.7%和8.8%;2）各模型的h_e在加載位移32 mm前相差不大；隨著加載位移的增加，M_c-4tf，M_c-5tf，M_c-6tf等模型h_e要明顯低于Base模型，其余各組模型的h_e與Base模型基本相等。

2.3.2 承載力與剛度分析

循環加載下，各模型的骨架曲線及剛度退化曲線，見圖11，部分特征點響應見表6。可見，各模型的骨架曲線基本重合，轉折位置無明顯差別，剛度退化曲線變化趨勢相同。總體上，模型的初始剛度、屈服荷載、峰值荷載及屈服位移等抗震性能指標隨削弱深度c的增加而略有減小，M_c-6tf模型均為最小值，較Base模型（最大）分別減小3.5%，2.8%，5.3%，6.0%，其余模型介于上述兩者之間。

3 加勁肋對結構抗震性能的影響

相關研究表明^［21］，加勁肋的布置可以減小耗能梁段塑性變形對結構抗震性能的不利影響，且高鋼規^［22］規定當耗能梁長度e介于2.6M_p/V_p～5M_p/V_p之間時（本文的耗能梁長度e=4.1M_p/V_p），應在距耗能梁端部1.5b_f處設置中間加勁肋，且中間加勁肋間距不應大于（52t_w-h/5）。

本文所提出的骨式削弱彎曲型耗能梁中部削弱處截面抗扭剛度較小，當加勁肋間距為1.5b_f時，耗能梁端部出現了不對稱的局部屈曲，進而耗能梁扭轉，見圖12 a），對整個結構的抗震性能產生了不利影響。基于此，研究了加勁肋間距對帶骨式削弱的彎曲型耗能梁偏心支撐模型（a=2b_f，c=3t_f）結構抗震性能的影響，模型的詳細參數及編號見表7。

圖13給出了單調及循環加載下各模型的荷載位移曲線。單調加載時，各模型荷載位移曲線在彈性階段基本重合，出現轉折的位置（耗能梁開始屈服）也無明顯差別。相較而言，耗能梁屈服之后，相同加載位移下，S₀.3b_f和S₀.7b_f模型的承載力基本相同，S₁.1b_f和S₁.5b_f模型的則略低，但整體差別在1.5%以內，可認為單調加載時改變加勁肋間距對結構承載力影響較小。循環加載時，S₀.3b_f，S₀.7b_f模型滯回曲線的包絡面積要大于 S₁.1b_f，S₁.5b_f模型。

圖14給出了循環加載下各模型的耗能能力結果。由圖14可知：1）S₀.3b_f與S₀.7b_f模型、S₁.5b_f和S₁.1b_f模型的耗能能力分別基本一致，但S₁.5b_f和S₁.1b_f模型耗能能力相對較差，分別為S₀.3b_f模型耗散總能量的90.1%和90.5%；2）各模型h_e在加載位移小于40 mm時無明顯差別；隨著加載位移的變大，S₀.7b_f，S₀.3b_f模型的h_e要明顯大于S₁.1b_f，S₁.5b_f模型。

圖15給出了循環加載下各模型的骨架曲線及剛度退化曲線。由圖15可知：1）各模型骨架曲線在彈性階段基本重合，轉折點位置亦無明顯差別；進入彈塑性階段后，S₀.7b_f，S₀.3b_f模型的承載力略高于S₁.1b_f，S₁.5b_f模型。這是由于僅改變加勁肋間距時，對耗能梁段的有效屈服面積幾乎無影響，故各模型的屈服荷載（相差1%以內）及屈服位移（相差3.9%以內）相差不大。耗能梁進入彈塑性階段后，較小的加勁肋間距可以有效抑制耗能梁端部翼緣的局部屈曲（見圖16 a）），間距較大時，抑制效果則不明顯，耗能梁端部翼緣局部屈曲明顯（見圖16 b）），使得S₁.1b_f和S₁.5b_f模型的峰值荷載要略小于S₀.7b_f和S₀.3b_f模型。2）各模型剛度退化曲線基本重合。相對來說，加載位移不大于8 mm時，S₀.3b_f，S₀.7b_f模型的剛度基本相等且略大于S₁.5b_f和S₁.1b_f模型，整體上各模型的初始剛度相差較小（3.6%以內）；之后隨著加載的繼續，各模型的剛度退化曲線相差不大。表8給出了循環加載下部分特征點響應。

總體上，帶骨式削弱的彎曲型耗能梁段加勁肋布置對結構的承載能力及耗能能力有一定影響。加勁肋間距較小時，能夠有效抑制耗能梁端部翼緣的局部屈曲。但當加勁肋間距過小時（S₀.3b_f模型），耗能梁段的剛度隨著加勁肋間距變小而有所增加，到加載后期使得耗能梁段翼緣端部的彎曲塑性鉸向剛度較小的框架梁處翼緣發展，造成了耗能梁與框架梁過度區域的梁段翼緣出現嚴重的局部屈曲現象（見圖17）。因此，對于骨式削弱的彎曲型耗能梁建議加勁肋的間距取0.7b_f。

4 結 論

研究了不同的削弱參數對帶骨式削弱的彎曲型耗能梁偏心支撐結構抗震性能的影響，并在此基礎上分析了耗能梁段上加勁肋布置對結構抗震性能的影響，得到如下結論。

1）總體上，帶骨式削弱的彎曲型耗能梁偏心支撐結構的承載力、剛度及耗能能力與Base模型相差不大。

2）帶骨式削弱的彎曲型耗能梁端部塑性變形區域增大，使得耗能梁端的耗能能力增強。結合實際耗能、承載力變化等抗震性能指標及用鋼量等，建議削弱起點a的取值在2h_f～3h_f之間，削弱深度c的取值在2t_f～4t_f之間。

3）耗能梁段上合理的加勁肋間距能夠有效抑制耗能梁端部翼緣的局部屈曲，改善帶骨式削弱的彎曲型耗能梁偏心支撐結構的抗震性能，故建議加勁肋的間距取0.7b_f左右。

本文對帶骨式削弱的彎曲型耗能梁偏心支撐結構進行研究時未改變耗能梁段的長度，今后擬在此模型的基礎上，針對耗能梁長度變化對結構性能的影響展開研究。

參考文獻/References：

［1］ MALLEY J O，POPOV E P.Shear Link in eccentrically braced frames［J］.Journal of Structural Engineering，1984，110（9）：2275-2295.

［2］ KAZEMZADEH-AZAD S，TOPKAYA C.A review of research on steel eccentrically braced frames［J］.Journal of Constructional Steel Research，2017，128：53-73.

［3］ 李通，王新武，時強，等.可替換式偏心支撐鋼框架抗震性能［J］.浙江大學學報（工學版），2021，55（9）：1725-1733.

LI Tong，WANG Xinwu，SHI Qiang，et al.Seismic performance of replaceable eccentrically braced steel frame［J］.Journal of Zhejiang University （Engineering Science），2021，55（9）：1725-1733.

［4］ 于海豐，吳楊周，馬康，等.剪切屈服型多耗能梁K形偏心支撐鋼框架抗震性能研究［J］.河北科技大學學報，2020，41（4）：356-364.

YU Haifeng，WU Yangzhou，MA Kang，et al.Study on seismic behavior of K-eccentrically braced steel structures with multi-shear links［J］.Journal of Hebei University of Science and Technology，2020，41（4）：356-364.

［5］ 程倩倩，連鳴，蘇明周，等.含可更換剪切型耗能梁段的鋼框筒結構抗震性能研究［J］.建筑鋼結構進展，2020，22（1）：35-46.

CHENG Qianqian，LIAN Ming，SU Mingzhou，et al.Seismic behavior study of steel framed-tube structure with replaceable shear links［J］.Progress in Steel Building Structures，2020，22（1）：35-46.

［6］ 王焱.K形彎曲型/彎剪型偏心支撐鋼框架結構抗震性能研究［D］.石家莊：河北科技大學，2020.

WANG Yan.Study on Seismic Performance of K-Shaped Eccentrically Braced Frame with Flexural/Flexural-Shear Yilding Links［D］.Shijiazhuang：Hebei University of Science and Technology，2020.

［7］ 李慎，蘇明周.基于性能的偏心支撐鋼框架抗震設計方法研究［J］.工程力學，2014，31（10）：195-204.

LI Shen，SU Mingzhou.A performance-based seismic design method for eccentrically braced steel frames［J］.Engineering Mechanics，2014，31（10）：195-204.

［8］ 陳小峰，鄧開國，郝際平.偏心支撐鋼框架能力設計方法研究［J］.鋼結構，2010，25（3）：15-21.

CHEN Xiaofeng，DENG Kaiguo，HAO Jiping.Study on capacity design method of eccentrically braced steel frames［J］.Steel Construction，2010，25（3）：15-21.

［9］ 趙根田，萬馨，王珊，等.耗能梁段長度對K形偏心支撐鋼框架抗震性能的影響［J］.鋼結構，2007，22（6）：6-9.

ZHAO Gentian，WAN Xin，WANG Shan，et al.The effect of link beam length on aseismic performance of K-type eccentrically braced steel frame［J］.Steel Construction，2007，22（6）：6-9.

［10］李新華，舒贛平.偏心支撐鋼框架的設計探討［J］.工業建筑，2001，31（8）：8-10.

LI Xinhua，SHU Ganping.Discussion on the design of eccentrically braced steel frame［J］.Industrial Construction，2001，31（8）：8-10.

［11］胡淑軍，宋固全，王湛.偏心支撐鋼框架基于性能的塑性設計方法研究［J］.建筑結構，2018，48（17）：111-117.

HU Shujun，SONG Guquan，WANG Zhan.Study of performance-based plastic design method for eccentrically braced steel frames［J］.Building Structure，2018，48（17）：111-117.

［12］陳世璽，吳楊周，于海豐，等.剪切型耗能梁K形偏心支撐鋼框架結構抗震性能研究［J］.建筑結構，2022，52（24）：50-56.

CHEN Shixi，WU Yangzhou，YU Haifeng，et al.Study on seismic behavior of K-shaped eccentrically braced steel frame structures with shear links［J］.Building Structure，2022，52（24）：50-56.

［13］葉重陽，王新武，時強，等.裝配式K型偏心支撐鋼框架抗震性能與震后替換［J］.振動與沖擊，2022，41（15）：224-232.

YE Chongyang，WANG Xinwu，SHI Qiang，et al.Aseismic performance and post-earthquake replacement of prefabricated K-type eccentrically frame braced steel frame［J］.Journal of Vibration and Shock，2022，41（15）：224-232.

［14］孫山川，王新武，孫海粟，等.不同長度耗能梁段偏心支撐框架受力性能［J］.河南科技大學學報（自然科學版），2020，41（1）：56-61.

SUN Shanchuan，WANG Xinwu，SUN Haisu，et al.Mechanical performance of eccentrically braced frames with different lengths of links［J］.Journal of Henan University of Science & Technology（Natural Science），2020，41（1）：56-61.

［15］王海濤，張素清，霍靜思.狗骨式鋼結構梁柱節點的沖擊荷載試驗研究和有限元分析［J］.振動與沖擊，2018，37（11）：107-114.

WANG Haitao，ZHANG Suqing，HUO Jingsi.Tests and FE analysis for impact behavior of RBS beam-column connections of steel frames［J］.Journal of Vibration and Shock，2018，37（11）：107-114.

［16］張愛林，楊忠帥，姜子欽，等.帶狗骨削弱蓋板的自復位預應力梁柱節點靜力性能研究［J］.建筑結構，2019，49（19）：119-125.

ZHANG Ailin，YANG Zhongshuai，JIANG Ziqin，et al.Static performance of self-resetting prestressed beam-column joints with dog-bone weakened cover plate［J］.Building Structure，2019，49（19）：119-125.

［17］DI BENEDETTO S，FRANCAVILLA A B，LATOUR M，et al.Pseudo-dynamic testing of a full-scale two-storey steel building with RBS connections［J］.Engineering Structures，2020，212.DOI： 10.1016/j.engstruct.2020.110494.

［18］田小紅，蘇明周，楊水成，等.高強鋼組合K形偏心支撐框架抗震性能對比分析［J］.建筑結構學報，2020，41（10）：42-49.

TIAN Xiaohong，SU Mingzhou，YANG Shuicheng，et al.Comparative analysis on seismic performance of high strength steel composite K-shaped eccentrically braced frames［J］.Journal of Building Structures，2020，41（10）：42-49.

［19］章衛松，吳楊周，于海豐，等.彎曲屈服型耗能梁K形偏心支撐結構抗震性能研究［J］.工程抗震與加固改造，2021，43（3）：57-65.

ZHANG Weisong，WU Yangzhou，YU Haifeng，et al.Study on seismic behavior of K-eccentrically braced structures with flexural links［J］.Earthquake Resistant Engineering and Retrofitting，2021，43（3）：57-65.

［20］傅恒菁.建筑結構試驗［M］.北京：冶金工業出版社，1992.

［21］李志剛. 偏心支撐框架的設計計算方法［D］.西安：西安建筑科技大學，2004.

LI Zhigang.The Design and Calculation of Eccentrically Braced Frames［D］.Xi′an： Xi′an University of Architecture and Technology，2004.

［22］JGJ 99—2015，高層民用建筑鋼結構技術規程［S］.