一類Caputo-Fabrizio型分數階微分方程的三次B樣條方法
胡行華, 蔡俊迎
(遼寧工程技術大學 理學院,遼寧 阜新 123000)
0 引 言
由于分數階微分方程的非局部性可用來描述不同物質的“記憶性”和“遺傳性”等物理特征,因此,其在眾多科學和工程領域中具有重要的應用價值.分數階導數有多種定義,較為常用的是Caputo型定義,作為弱奇異的分數階導數定義,Caputo型定義比其他經典定義更適合于分數階微分方程的描述,在進行Laplace變換時,其物理意義更加明確,因此,眾多學者對Caputo型分數階微分方程進行了廣泛研究[1-2],但缺點是其定義中存在一個奇異核.2015年,Caputo和Fabrizio[3-4]提出了一個新的分數階導數定義,即Caputo-Fabrizio型定義,其為指數函數與一階導數的卷積,不存在奇異項,修正后的定義形式[5]如下:
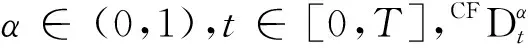
(1)
式中,α∈(0,1),f(t)∈C[0,T]為線性光滑函數,且問題(1)存在唯一解u(t).
然而,對于一般的右端項,通常很難獲得精確解,因此在該定義下,方程數值方法的研究顯得很有必要.許多學者對此展開了研究,2017年,Owolabi等[6]提出了線性和非線性具有Caputo-Fabrizio導數的分數階微分方程的三步Adams-Bashforth格式,該格式具有條件穩定性.2020年,Cao等[14]針對Caputo-Fabrizio型分數階常微分方程,構造了一種改進block-by-block算法.Guo等[15]基于Lagrange多項式,提出了求解Caputo-Fabrizio型分數階微分方程的有限差分方法.2021年,Al-Smadi等[16]提出了一個Caputo-Fabrizio型非線性分數階Abel微分方程的再生核方法,該方法具有較好的穩定性.Douaifia等[17]基于Newton插值提出了一種適用于Caputo-Fabrizio型分數階微分方程的預測-校正數值格式.何廣婷[18]提出了一種基于L2方案和遞推關系的快速高階數值方法,求解Caputo-Fabrizio型的分數階常微分方程,該算法大大降低了存儲容量和總計算成本.
通過現有文獻發現,這些數值方法還存在一些不足之處:求解效率較低,求解精度有待進一步提高等.眾所周知,樣條插值函數非常接近被插值函數[19],而三次B樣條函數具有計算簡單、穩定性、收斂性有保證且易于在計算機上實現等優點,可以克服現有方法的缺點.本文基于分數階微積分基本定理和三次B樣條函數構造Caputo-Fabrizio型分數階微分方程的數值格式.并對所構造的三次B樣條方法的誤差進行估計,對收斂性和穩定性進行理論證明.數值實驗表明,三次B樣條方法具有一定的可行性和有效性,在計算精度和計算效率上具有明顯優勢.
1 基 礎 知 識
1.1 Caputo-Fabrizio分數階導數的基本定義
下面,給出Caputo分數階導數具體的定義形式.
定義1[20]函數u(t)的α階Caputo分數階導數定義為
(2)
其中,u(t)∈H1(0,b),b>0,α∈(0,1),Γ(·)為Gamma函數.
2015年,Caputo和Fabrizio[3]提出了一個具有光滑核的分數階導數新定義,其定義如下.
定義2[3]令u(t)∈H1(0,b),b>0,并且α∈(0,1),通過用函數exp(-α(t-τ)/(1-α))替換核(t-τ)-α,用M(α)/(1-α)替換1/Γ(1-α),函數u(t)的α階Caputo-Fabrizio分數階導數定義為
(3)
其中,M(α)是一個標準化函數.與式(2)相比,新定義在t=τ時無奇異核.
Losada和Nieto[5]對Caputo-Fabrizio分數階導數進行了修正,首先有以下定義.
定義3[5]假設u(t)∈H1(0,b),α∈(0,1),將Caputo-Fabrizio分數階導數定義為
(4)
Losada和Nieto[5]提供了M(α)的一個顯式公式:M(α)=2/(2-α).將M(α)的顯式公式代入式(4),即得式(3)修正后的公式[5]:
(5)
接下來,對于一個一般的α,α∈(0,1)階Caputo-Fabrizio型分數階微分方程(1),利用分數階微積分基本定理[5]可將其轉換為
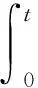
(6)
由上式易得,當且僅當f(0)=0時,式(1)中的u(t)滿足初始條件u(0)=u0.鑒于此,求解式(1)的數值解即轉化為逼近式(6)右端項中積分的問題.
1.2 m次B樣條插值函數
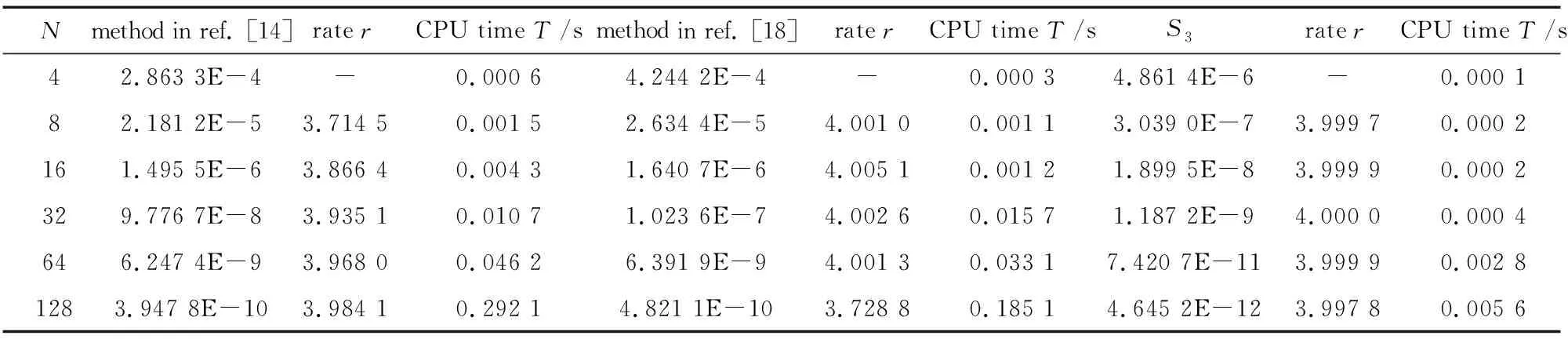
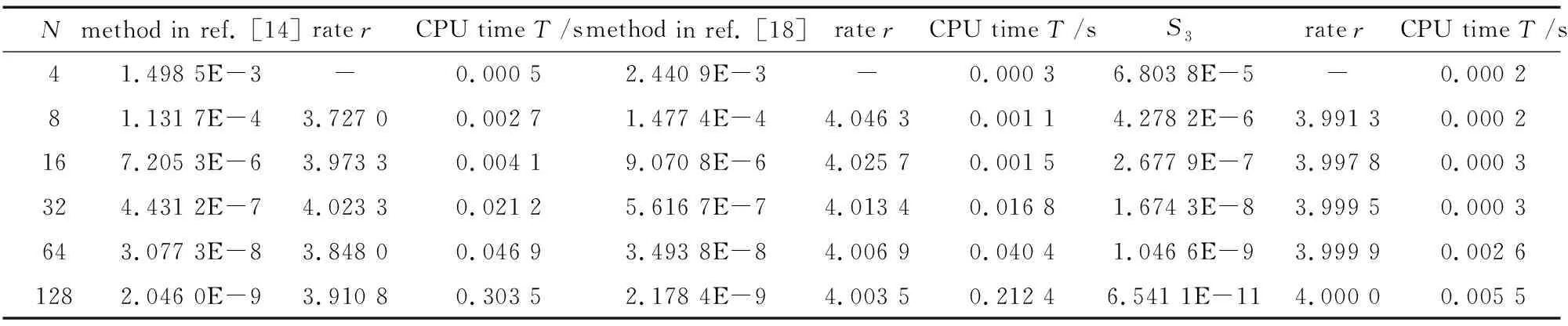
將區間[0,T]剖分成等距的N個小區間,對于給定的任一整數N>0,其小區間的步長為h=T/N.對于j=0,1,…,N,tj=jh,并且0=t0 (7) (8) (9) 在m次B樣條插值函數中,相比于低次和高次的B樣條函數,三次B樣條函數具有需要較少的信息、精度高、計算簡單和易于實現編程的優勢[23].因此,本文使用三次B樣條函數求解一類Caputo-Fabrizio型分數階微分方程. 首先,考慮右端項與u(t)無關的線性初值問題(1),即 (10) 使用三次B樣條插值函數S3(τ)來近似代替式(6)中積分里的函數f(τ),可得 [βj+1(h3+3h2(τ-tj-1)+3h(τ-tj-1)2-3(τ-tj-1)3)+βj+2(τ-tj-1)3]dτ+ (1-α)f(tk)= 其中,1≤k≤N.由此得出S3公式,并使用符號uS3(tk)表示,即 (11) 其中,β0,β1,…,βN+2為常系數,求出β的N+3個系數則得到uS3(tk). 根據三次B樣條插值函數理論,uS3(tk)滿足N+1個插值條件:在節點tj上的函數值yj=f(tj)(j=0,1,…,N),且S3(tj)=yj(j=0,1,…,N)成立.此外,還需要2個邊界條件才能求出β的N+3個系數,邊界條件有多種類型[22].為便于求解,本文選擇普適性較強的固定邊界條件S′3(t0)=f′(t0),S′3(tN)=f′(tN).由插值條件和邊界條件可得系數β滿足線性方程組Mβ=f,其中f=[f′(t0),f(t0),f(t1),…,f(tN),f′(tN)]T,β=[β0,β1,…,βN+2]T,且矩陣M為 矩陣M是對角占優矩陣,因此系數β是唯一確定的,使用追趕法[22]即可獲得.其他邊界類型的三次B樣條函數也可以類似應用,且β同樣易獲得. 接下來,考慮右端項與u(t)有關的線性初值問題[6]: (12) 其中,g(t)是一個已知函數.根據式(12),有 (1-α)[u(tk)+g(tk)]= (13) (14) 根據上式,需要u′(0)和u′(tN)的值,它們分別由以下四階正向差分公式和四階反向差分公式[24]來近似,即 (15) 由式(13)—(15)即可求得u(tk)的近似數值uk. 首先,在對三次B樣條方法進行誤差估計之前,給出以下定理. 定理1[25]設函數f∈C4[0,T],則函數f與三次樣條插值函數S3之間的距離為 定理2 若f∈C4[0,tk],且R(tk)=u(tk)-uS3(tk),則有 (16) 證明對于任意的1≤k≤N,根據定理1可得 |R(tk)|=|u(tk)-uS3(tk)|= 定理2證畢. 下面給出三次B樣條方法的收斂性分析. 定理3 三次B樣條方法在區間[0,T]上是一致收斂的,即當h→0時,‖R3(tk)‖∞→0. 證明根據定理2中三次B樣條方法的誤差估計,可得 其中,f∈C4[0,T],當h→0時,有 因此,此數值格式在區間[0,T]上是一致收斂的.定理3證畢. 接下來對三次B樣條方法進行穩定性分析. 定理4 三次B樣條方法在區間[0,T]上是無條件穩定的. 因此,三次B樣條方法是無條件穩定的.定理4證畢. 其中,N為各數值方法在[0,1]區間分割的份數,也為待求未知量的個數,代表以上各數值方法在數值求解的計算量大小,且3種數值方法的帶狀矩陣皆采用Gauss消元法來計算.所有程序均在CPU為Inter Core i5 Processor 2.30 GHz、內存為8 GB的筆記本電腦環境下運行,利用MATLAB 2018a平臺實現. 例1 本文考慮具有兩個不同右端項的初值問題[14,18]: 情況1 (17) 情況2 (18) 兩種情況的初值均為u0=0,精確解均為u(t)=t3,并且右端項中G1(t)和G2(t)分別為 G2(t)=G1(t)-t3. 可見,情況1與情況2均屬于線性初值問題,情況2的右端項與u(t)有關,且G1(0)=0,G2(0)+u(0)=0. 下面,使用本文提出的三次B樣條方法分別求解情況1和情況2的初值問題. 求解情況1 已知插值條件S3(tj)=G1(tj)(j=0,1,…,N)和固定邊界條件S′3(0)=G′1(0),S′3(1)= G′1(1)成立,使用三次B樣條方法求解不同的分割數N(N=4,8,16,32,64,128)與不同α(α=0.3,0.7)階的Caputo-Fabrizio型分數階微分方程數值解,并與文獻[14]中改進的block-by-block算法和文獻[18]中的快速高階數值方法進行對比.當α=0.3時,3種數值方法的最大誤差和收斂階對比如表1所示,3種數值方法的最大誤差比較如圖1所示.當α=0.7時,3種數值方法的最大誤差和收斂階對比如表2所示,3種數值方法的最大誤差比較如圖2所示. 表1 當α=0.3時,3種數值方法的最大誤差和收斂階(情況1)Table 1 Maximum errors and convergence orders of 3 numerical methods for α=0.3 (case 1) 表2 當α=0.7時,3種數值方法的最大誤差和收斂階(情況1)Table 2 Maximum errors and convergence orders of 3 numerical methods for α=0.7 (case 1) 圖1 當α=0.3時,3種數值方法的最大誤差(情況1) 圖2 當α=0.7時,3種數值方法的最大誤差(情況1)Fig.1 Maximum errors of the 3 numerical methods for α=0.3 (case 1) Fig.2 Maximum errors of the 3 numerical methods for α=0.7 (case 1) 由表1和表2可知,在不同的分數階次下,與改進的block-by-block算法相比,本文方法的誤差明顯更小,數值逼近效果更佳,且收斂階較高.與快速高階數值方法相比,本文方法的誤差明顯更小,數值逼近效果更佳,收斂階相當.此外,本文數值方法的CPU時間較短,具有可觀的計算效率.顯然,采用三次B樣條方法求解Caputo-Fabrizio型分數階微分方程比其他兩種方法更加有效. 由圖1和圖2可知,改進的block-by-block算法和快速高階數值方法在各分割數下的最大誤差相差不多,與以上兩種數值方法相比,本文方法的最大誤差明顯更小,數值逼近效果更佳. 下面,固定分割數N=100,使用三次B樣條方法分別求解情況1中不同階次α(α=0.2,0.4,0.6,0.8) 的初值問題,其各節點處的絕對誤差結果如圖3所示.固定分割數N=10,本文方法在階次α取不同值時所得各節點的數值解如圖4所示. 由圖3可知,不同的階次α導致本文方法的絕對誤差有所不同,階次α越小,各節點處的絕對誤差越小,數值逼近的效果越佳.由圖4可知,當階次α取不同值時,各節點處的數值解均保持平穩狀態,本文方法在t∈[0,1]時具有良好的穩定性. 表3 當α=0.3時,3種數值方法的最大誤差和收斂階(情況2)Table 3 Maximum errors and convergence orders of 3 numerical methods for α=0.3 (case 2) 表4 當α=0.7時,3種數值方法的最大誤差和收斂階(情況2)Table 4 Maximum errors and convergence orders of 3 numerical methods for α=0.7 (case 2) 圖5 當α=0.3時,3種數值方法的最大誤差(情況2) 圖6 當α=0.7時,3種數值方法的最大誤差(情況2)Fig.5 Maximum errors of the 3 numerical methods for α=0.3 (case 2) Fig.6 Maximum errors of the 3 numerical methods for α=0.7 (case 2) 由表3和表4可知,在不同的分數階次下,與改進的block-by-block算法相比,本文方法的誤差明顯更小,數值逼近效果更佳,且收斂階較高.與快速高階數值方法相比,本文方法的誤差明顯更小,數值逼近效果更佳,收斂階相當.此外,本文數值方法的CPU時間較短,具有可觀的計算效率.顯然,三次B樣條方法在求解Caputo-Fabrizio型分數階微分方程時比其他兩種方法更加有效. 由圖5和圖6可知,改進的block-by-block算法和快速高階數值方法在各分割數下的最大誤差相差不多,與以上兩種數值方法相比,本文方法的最大誤差明顯更小,數值逼近效果更佳. 接下來,固定分割數N=100,使用三次B樣條方法分別求解情況2中不同階次α(α=0.2,0.4,0.6,0.8) 的初值問題,其各節點處的絕對誤差結果如圖7所示.固定分割數N=10,本文方法在階次α取不同值時所得各節點的數值解如圖8所示. 圖7 不同α值時各節點的絕對誤差(情況2) 圖8 不同α值時各節點的數值解(情況2)Fig.7 Absolute errors of each node with different α values (case 2) Fig.8 Numerical solutions of each node with different α values (case 2) 由圖7可知,不同的階次α導致本文方法的絕對誤差有所不同,階次α越小,各節點處的絕對誤差越小,數值逼近的效果越佳.由圖8可知,當階次α取不同值時,各節點處的數值解均保持平穩狀態,本文方法在t∈[0,1]時具有良好的穩定性. 例2 下面將驗證三次B樣條方法的穩定性,考慮如下的初值問題[14,18]: (19) 其中,精確解為u(t)=sint,右端項滿足f(0)=0. 已知插值條件S3(tj)=f(tj)(j=0,1,…,N)和固定邊界條件S′3(0)=f′(0),S′3(1)=f′(1)成立,固定分割數N=10 000,使用3種數值方法分別求解不同的α(α=0.3,0.5,0.7)階的Caputo-Fabrizio型分數階微分方程數值解,一直計算到T=1 000.當α=0.3,0.5,0.7時,3種數值方法在不同節點處的絕對誤差(|ε|=|u(tk)-uk|)和相對誤差(ε′=|ε|/u(tk))結果分別如表5、表6和表7所示,3種數值方法的相對誤差對比如圖9、圖10和圖11所示. 表5 α=0.3,N=10 000時,3種數值方法在不同節點處的絕對誤差和相對誤差Table 5 The absolute and relative errors of the 3 numerical methods at different nodes for α=0.3,N=10 000 表6 α=0.5,N=10 000時,3種數值方法在不同節點處的絕對誤差和相對誤差Table 6 The absolute and relative errors of the 3 numerical methods at different nodes for α=0.5,N=10 000 表7 α=0.7,N=10 000時,3種數值方法在不同節點處的絕對誤差和相對誤差Table 7 The absolute and relative errors of the 3 numerical methods at different nodes for α=0.7,N=10 000 圖9 當α=0.3時,3種數值方法的相對誤差 圖10 當α=0.5時,3種數值方法的相對誤差Fig.9 Relative errors of 3 numerical methods for α=0.3 Fig.10 Relative errors of 3 numerical methods for α=0.5 圖11 當α=0.7時,3種數值方法的相對誤差Fig.11 Relative errors of 3 numerical methods for α=0.7 由表5所示,與改進的block-by-block算法和快速高階數值方法相比,三次B樣條方法在不同節點處的絕對誤差和相對誤差較小,經過長時間的計算,不同節點上的數值解均可以很好地逼近精確解,并且本文方法的CPU時間較短,計算效率可觀.由圖9所示,3種數值方法的相對誤差在個別節點處均有起伏,但與其他兩種方法相比,本文方法的平穩狀態更佳.此外,3種數值方法相對誤差的方差分別為1.074 4×10-10,7.603 0×10-12和5.157 2×10-13.顯然,三次B樣條方法在求解Caputo-Fabrizio型分數階微分方程時比其他兩種方法更加穩定. 由表6所示,與改進的block-by-block算法和快速高階數值方法相比,三次B樣條方法在不同節點處的絕對誤差和相對誤差較小,經過長時間的計算,不同節點上的數值解均可以很好地逼近精確解,并且本文方法的CPU時間較短,計算效率可觀.由圖10所示,3種數值方法的相對誤差在個別節點處均有起伏,但與其他兩種方法相比,本文方法的平穩狀態更佳.此外,3種數值方法相對誤差的方差分別為6.410 8×10-10,3.654 9×10-11和2.853 2×10-13.顯然,三次B樣條方法在求解Caputo-Fabrizio型分數階微分方程時比其他兩種方法更加穩定. 由表7所示,與改進的block-by-block算法和快速高階數值方法相比,三次B樣條方法在不同節點處的絕對誤差和相對誤差較小,經過長時間的計算,不同節點上的數值解均可以很好地逼近精確解,并且本文方法的CPU時間較短,計算效率可觀. 圖11(a)為當α=0.7時3種數值方法的相對誤差對比,圖11(b)為快速高階數值方法和三次B樣條方法的相對誤差對比.由圖11所示,3種數值方法在個別節點處均有起伏,但與其他兩種方法相比,本文方法的平穩狀態更佳.此外,3種數值方法相對誤差的方差分別為4.188 4×10-9,1.514 5×10-10和1.051 7×10-10.因此,三次B樣條方法在求解Caputo-Fabrizio型分數階微分方程時比其他兩種方法更加穩定. 本文將三次B樣條方法應用于Caputo-Fabrizio定義下的分數階微分方程的數值求解.基于分數階微積分基本定理和三次B樣條函數,構造了求解α階線性Caputo-Fabrizio型分數階微分方程數值解的三次B樣條方法.對所構造的數值方法進行了誤差估計,并對其收斂性和穩定性進行了理論證明.實驗結果表明:三次B樣條方法具有一定的有效性,且具有4階收斂階和良好的穩定性;在求解線性初值問題時,與改進的block-by-block算法和快速高階數值方法相比,三次B樣條方法明顯具有較高的精度和較快的收斂速度,且計算復雜度低,計算成本小.綜上,三次B樣條方法在求解Caputo-Fabrizio型分數階微分方程時具有明顯優勢,為一類α階Caputo-Fabrizio型分數階微分方程的數值求解提供了新的選擇.
2 三次B樣條方法數值格式的構造
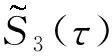

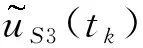
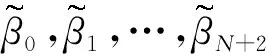
3 三次B樣條方法的誤差估計、收斂性和穩定性分析
3.1 三次B樣條方法的誤差估計
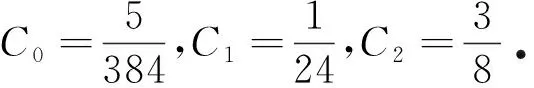
3.2 三次B樣條方法的收斂性分析
3.3 三次B樣條方法的穩定性分析
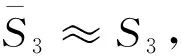
4 數 值 算 例
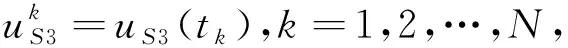
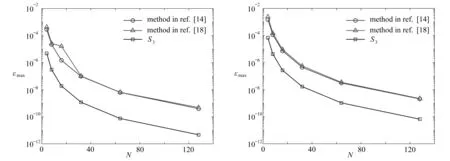

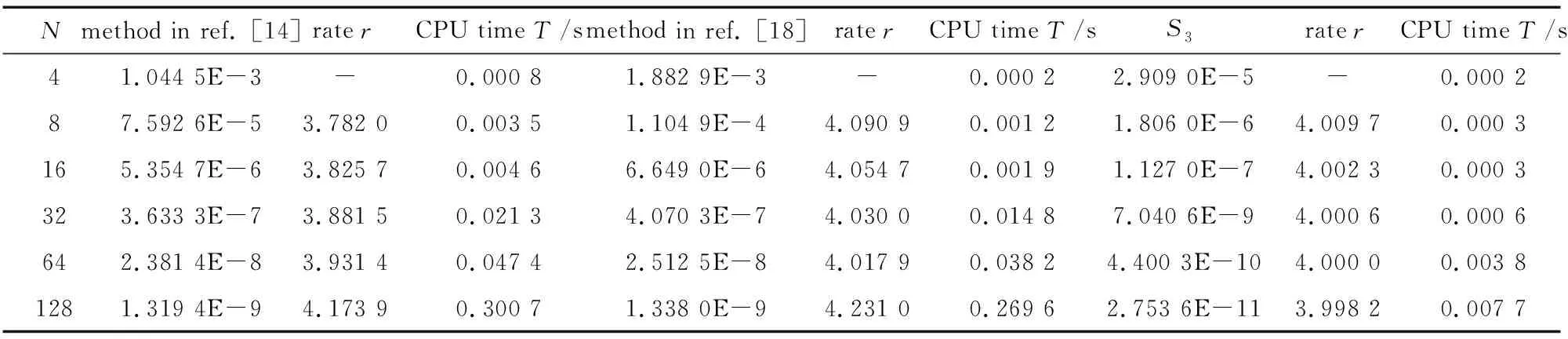
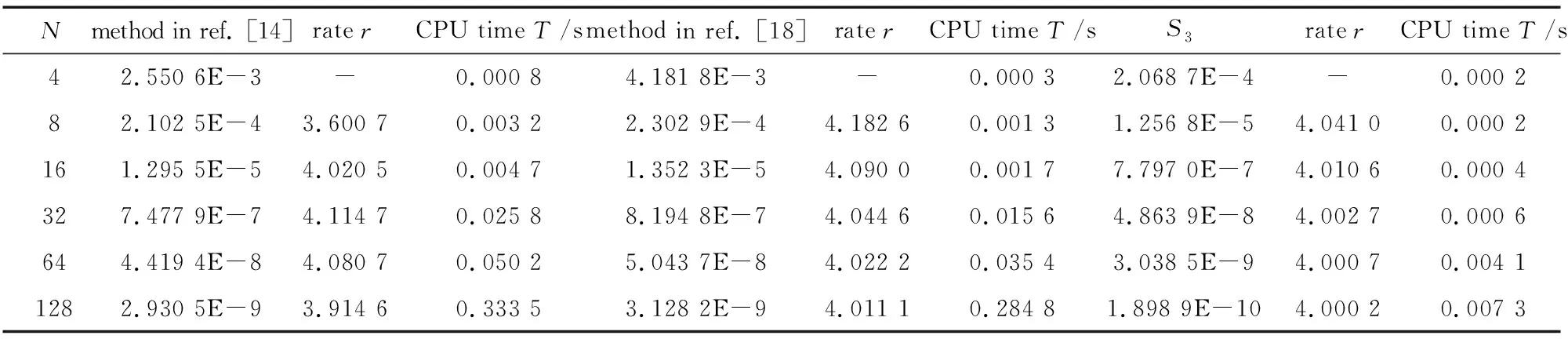
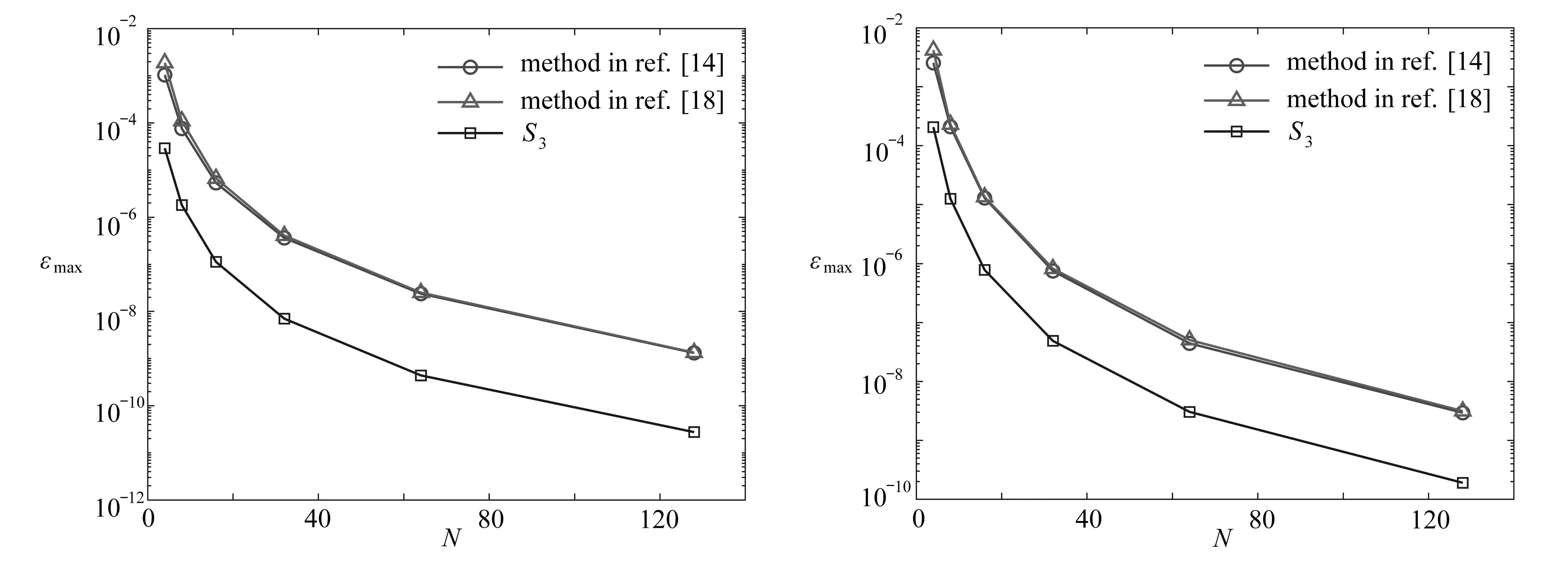
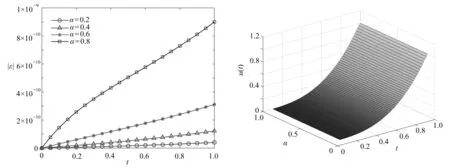
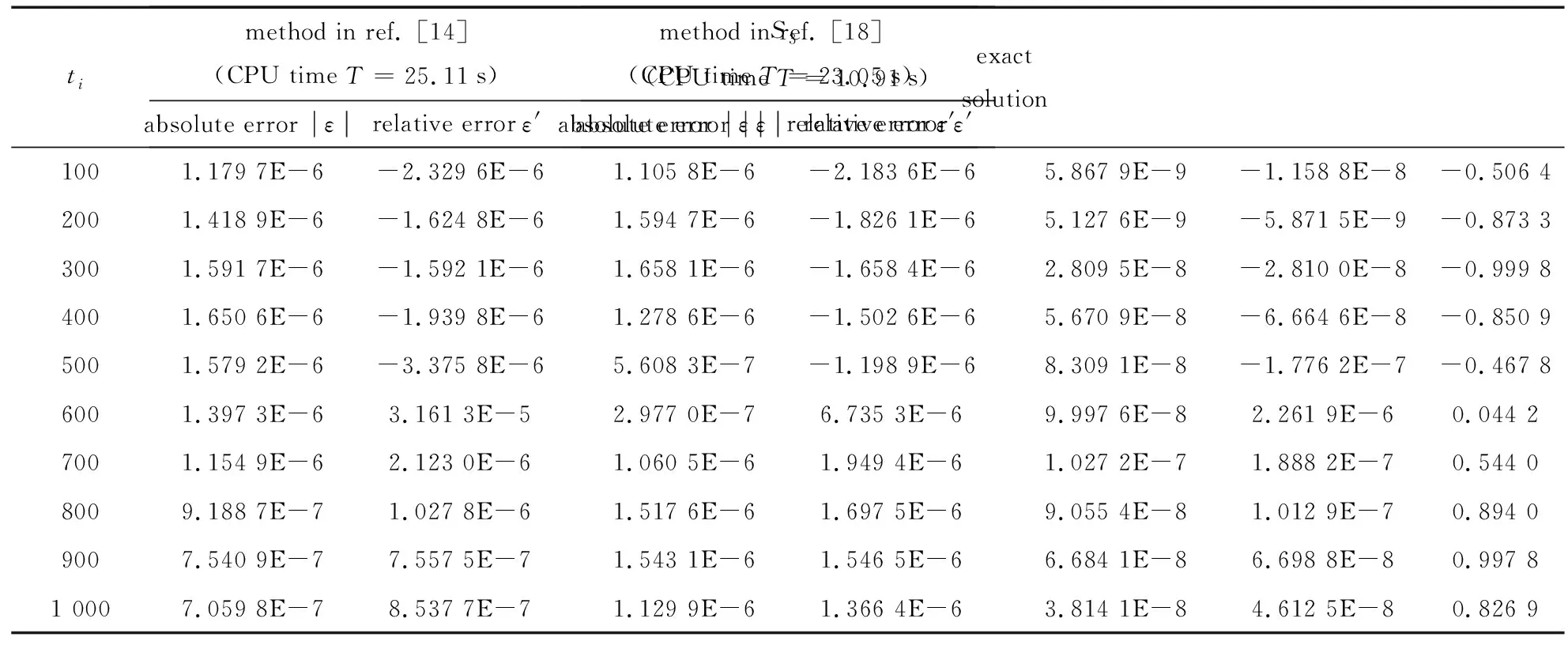
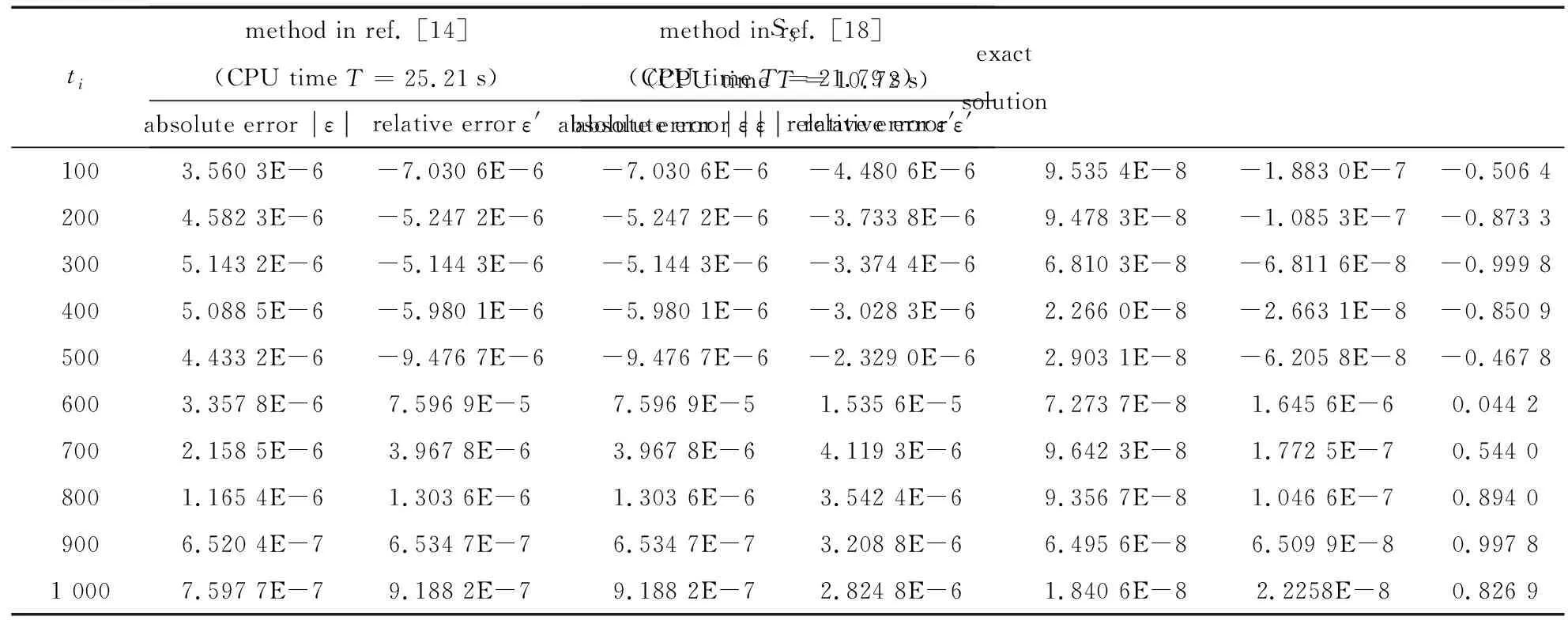
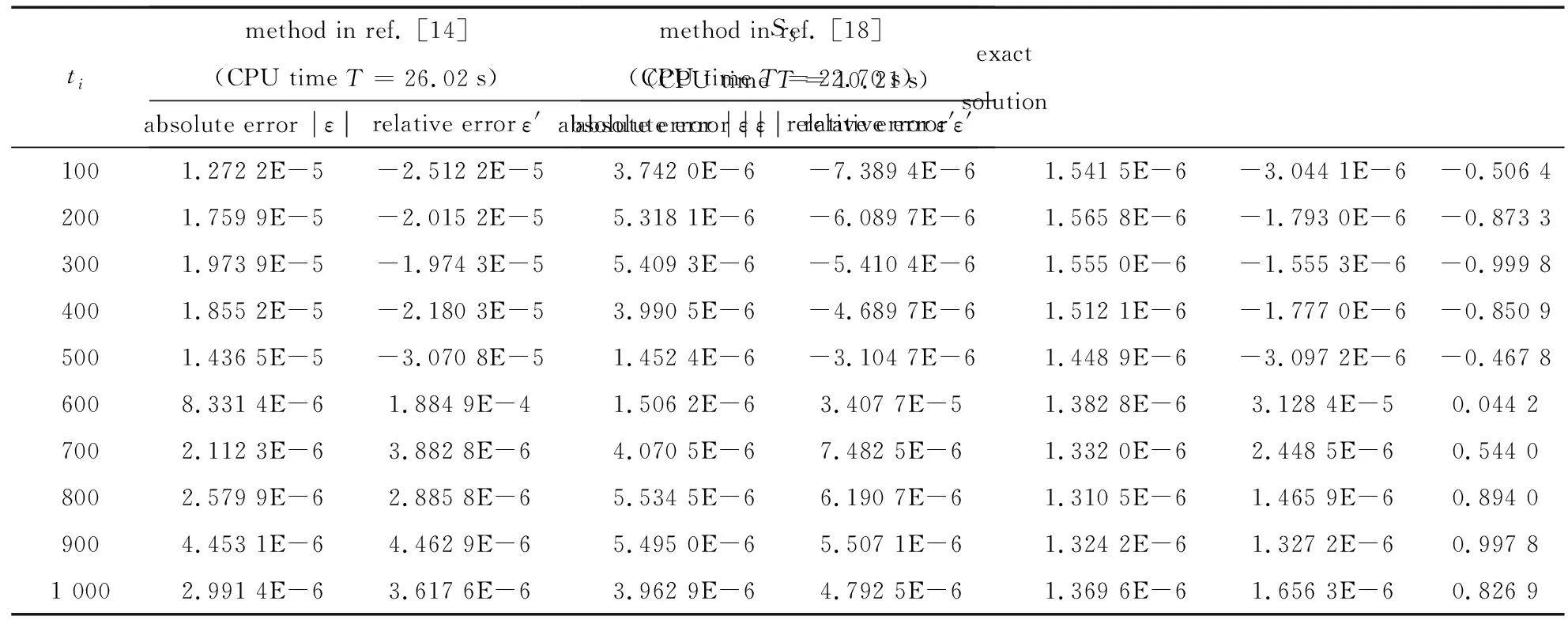
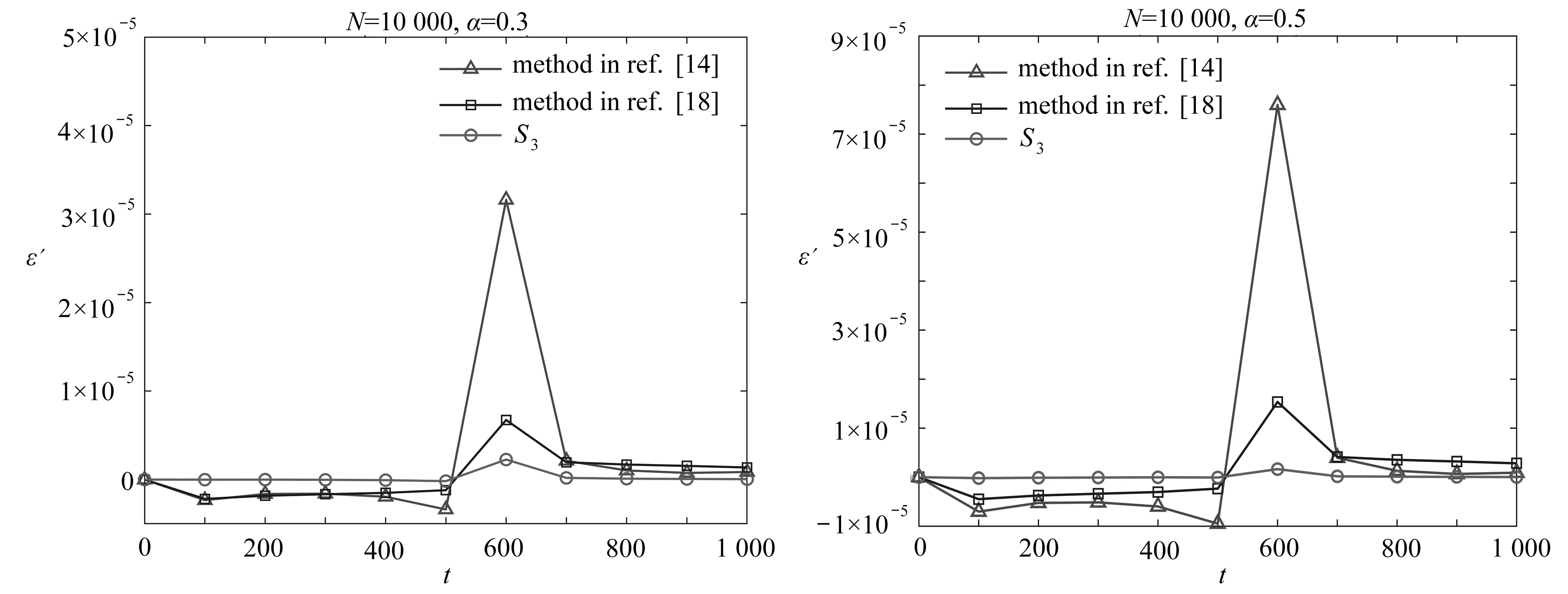
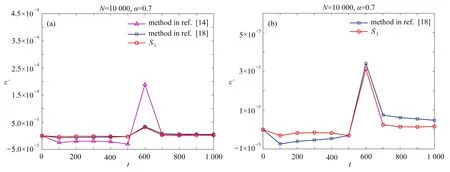
5 結 論

